弹性飞机阵风缓和鲁棒控制研究

傅　军，万　婧，艾剑良

(复旦大学 航空航天系，上海 200433)



弹性飞机阵风缓和鲁棒控制研究

傅军，万婧，艾剑良

(复旦大学 航空航天系，上海 200433)

摘要：阵风干扰一直严重影响着飞机的飞行稳定性、性能和乘坐舒适度.基于现代鲁棒控制理论，研究了在气动弹性效应影响下的飞机阵风载荷减缓控制器的设计方法.首先根据气动弹性状态空间模型得到某通用飞机在纵向平面内的运动方程.然后在Dryden阵风模型作为外界干扰输入下，对弹性飞机标称系统设计了H∞控制器，取得了良好的阵风减缓效果，使得翼尖相对位移和质心加速度的均方根分别减小了66%和23.7%，同时讨论了评价输出加权函数的选择方法.由于系统在真实的环境下会存在不确定性，结合构建的不确定模型，设计了μ综合控制器，仿真结果表明，对于H∞控制器不再适用的不确定性系统，μ控制器能够满足鲁棒稳定性和鲁棒性能.

关键词：弹性飞机； 气动弹性方程； 阵风缓和； 鲁棒控制

阵风干扰会严重影响飞机在飞行过程中的性能，降低乘坐舒适度，造成结构疲劳，减小飞机寿命.在20世纪60年代，国外就开始了飞机阵风载荷减缓控制技术的研究，然而大多数研究都集中在刚性飞机模型的控制器设计上，实际飞机结构是弹性体，特别是随着现代飞机设计中大柔性、轻结构的趋势越来越明显[1]，相应的气动弹性问题也越来越不容忽视.所以对阵风载荷减缓主动控制的进一步研究必须要考虑到飞机的气动弹性特性.

建立一个用于控制器设计的气动弹性方程最主要的困难在于非定常气动力的计算.由Albano等[2]在1969年提出的计算3维亚音速简谐振荡非定常空气动力的偶极子网格法，被Rodden等[3]加以改进后，能够处理任意多翼多体的飞机外形组合，从而成为目前亚音速可压缩情况下非定常气动力计算的首选方法.非定常气动力是在离散的减缩频率上计算的，然而现代控制分析方法都要求非定常气动力能够表示在整个拉普拉斯域(s平面)内，所以需要将其近似为拉普拉斯算子s的有理函数.Karpel[4]提出的最小状态近似方法得到了非定常气动力影响矩阵的有理表达，并且建立了弹性飞机的状态空间模型.本文基于此方法建立了某通用飞机在纵向平面内的弹性方程.

随着对飞机气动弹性特性认识的深入，考虑飞机结构弹性的阵风载荷减缓控制越来越受到重视.Karpel[4]在建立气动弹性系统的状态方程后，为典型机翼截面模型的阵风减缓设计了一个常数增益的简单控制器，以验证其气动弹性模型的广泛可用性.Zeng等[5]使用自适应前馈控制方法有效地减缓了F/A-18的弹性模型在阵风干扰下的响应.Aouf等[6]和Cook等[7]分别在各自的文章中借助鲁棒控制方法对弹性飞机进行阵风缓和主动控制.因为气动弹性建模的复杂性，建立的气动弹性模型总是涉及各种各样的不确定参数，比如结构阻尼比和液力作动器参数、气动力系数以及系统高频动态特性方面的不确定性.文献[8]在研究B-52飞机弹性模型的阵风减缓控制时，使用μ分析方法探讨了不确定性模型的控制方法.

本文采用Dryden阵风模型作为外界干扰输入，研究了弹性飞机标称系统H∞控制器的设计方法.为系统构建了不确定性模型后，设计了μ控制器，保证了系统存在不确定性情况下的鲁棒稳定性和鲁棒性能.

1弹性飞机模型

1.1气动弹性运动方程

飞机的气动弹性行为是由飞机的惯性力、结构弹性力、气动力和外界附加力相互耦合作用的结果.建立弹性飞机的运动方程一般要通过结构有限元和气动有限元方法进行计算，得到的方程的系数矩阵的阶次是非常大的，不利于后续的进一步分析.而通常的做法是将方程变换到模态坐标中，利用低阶振动模态来近似弹性结构的振动行为，得到的模态方程的阶次将大幅降低.分析表明，对于单独机翼结构，用不超过10个低阶振动模态来近似，精度已经足够[9].

使用模态分析方法，并对结构有限元中力的平衡方程进行拉普拉斯变换，得到弹性飞机分析的一般方程[10]：

([M]s2+[B]s+[K]+q∞[Qa(s)]){ξ(s)}=-([Mc]s2+q∞[Qc(s)]){δ(s)}-(q∞/V)[Qw(s)]{w(s)},

(1)

其中：s为拉普拉斯算子；[M]、[B]和[K]分别为飞机的广义质量、阻尼和刚度矩阵；ξ为广义模态坐标；δ为控制舵面输入；w(s)为外界阵风干扰输入；q∞为动压；V为来流速度；Mc为飞机模态与舵面偏转模态的耦合质量矩阵；Q(s)=[Qa(s)Qc(s)Qw(s)]为非定常气动力影响矩阵，Qa、Qc和Qw分别表征由结构弹性变形、控制舵面偏转和外界阵风引起的作用于机身的气动力.

非定常气动力影响矩阵Q的计算非常复杂，这也是建立飞机气动弹性模型过程中最重要的一步.本文中Q的计算借助气动弹性分析软件ZAERO[11]来完成，方程(1)中Qa、Qc和Qw的符号设定为与ZAERO软件中规定的一致.

非定常气动力影响矩阵Q是在离散的减缩频率k上计算的，而随着控制理论的发展和先进气动理念的出现，特别是一般的现代控制理论都是建立在系统的线性状态空间模型的基础上，所以需要将Q转化到时域中.在气动弹性控制领域，主要有两种方法： Roger近似法[12]和最小状态近似法[4]，即将离散频率点处计算得到的非定常气动力延拓至拉普拉斯域中并用有理函数表达，通过有理函数拟合得到未知系数，然后引入附加气动力状态变量得到气动力状态变量所满足的时域微分方程，最后将整个气动弹性方程表达在状态空间中.

因为Roger近似法需要引入的附加气动力状态变量的维数较高，使得状态方程的规模增大，所以这里选择最小状态近似法：

(2)

其中[Ai]=[AaiAciAw i]，[E]=[EaEcEw].设附加气动力状态量xa(s)为：

(3)

由(1)～(3)式可以得到气动弹性状态方程为：

(4)

考虑控制面舵机的动态特性，将舵机的动态模型表示为如下传递函数：

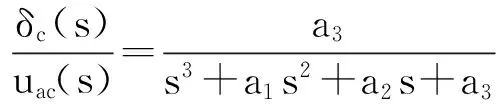
(5)

所以考虑舵机模型的飞机增广气动弹性状态方程为：

(6)

方程(6)为包含阵风干扰输入和舵机模型的气动伺服弹性问题的一般方程，可以应用于任意飞机的阵风响应分析和阵风载荷减缓控制研究.

1.2仿真实例

本文选择某通用飞机[13]作为研究对象，如图1所示.机身长度为22m，全翼展长19m，机翼平均弦长为2.2m.飞机的飞行状态设定为在7000m高度下以218m/s(Mach=0.7)的速度巡航飞行.

由于飞机机翼在纵向有着较大受力面积，在高空巡航状态下阵风对飞机的影响主要表现在垂直方向上.所以为了分析的简便，这里仅考虑飞机在纵向平面内的运动.为了对阵风载荷的影响进行主动控制，飞机的外侧副翼和平尾上的升降舵被用来作为控制舵面，即{u}={uaileron,uelevator}T.根据文献[14]中的参数，(5)式中舵机的动态特性参数为a1=6751689，a2=66157.39，a3=259.97.

本文借助结构有限元软件Nastran和气动弹性分析软件ZAERO来计算建立气动弹性模型所需要的数据.在模态坐标中，全机使用21个低阶振动模态来近似结构的弹性行为.

因为这里只考虑飞机的纵向运动，所以振动模态中的非纵向模态将被舍弃，剩余9个纵向振动模态，而其中一个模态为飞机上下沉浮运动的刚性模态，会导致得到的状态矩阵中含有零特征值，所以也要移除.余下的8个振动模态，加上9个附加气动力状态量和6个因舵机动态模型而加入的状态量，最后得到一个具有31阶系数矩阵的状态方程.

阵风减缓是通过主动控制技术使飞机对外部阵风干扰输入的响应最小化，从而达到减小机翼弯矩、延长疲劳寿命、改善乘坐品质和乘员舒适度的目的.从这些目的出发，这里选择飞机模型的量测输出量为飞机的俯仰角、翼尖相对翼根的垂直位移和飞机质心的垂直加速度，即y={θ,xd,ac}T，其中xd=xwingtip-xwingroot.输出方程为：

{y}=[C]{x}+[Dw]{w}+[D]{u}.

(7)

2阵风模型

目前广泛使用的与实际观测数据吻合很好的阵风模型为Dryden模型和Von Karman模型.由于Dryden模型相对简单，这里被用来作为飞机高空巡航时的阵风干扰信号模型.Dryden模型是以功率谱密度函数的形式表述的[15].

为了能够得到符合此模型的阵风干扰信号，需将功率谱密度为1的白噪声通过构造的滤波器.根据Dryden模型的功率谱密度，滤波器的传递函数为：

其中：σw为均方根阵风速度；Lw是紊流尺度；V为飞行速度；ω为圆频率，单位为rad/s.

根据该通用飞机的飞行环境参数，计算得到Lw=533.4m，σw=6.4m/s.

3H∞控制器设计

对于弹性飞机的阵风减缓控制问题，基于已经得到的飞机状态方程(6)和输出方程(7)，选择评价输出为{z}=W·{z′}=W·{yT,uT}T，即在抑制因阵风干扰w而引起的输出y的同时保证控制输入量u不会超过允许的舵面操纵范围.W=diag([Wy,Wu])为评价输出的加权函数.

弹性飞机阵风缓和H∞控制问题的具体结构如图2(b)所示，相应的方程描述为：

(8)

系统传递函数的正无穷范数可以看作是系统从输入到输出的最大能量增益.控制的目的是减小这种能量增益，使得系统的评价输出z受干扰输入w的影响最小.对于实际系统来说，输出信号之间的物理单位不尽相同，对同一干扰的响应在数值上差别可能很大，所以如果直接把系统的量测输出作为被抑制信号，将很可能得不到一个理想的控制器，甚至导致问题无解.所以加权函数W的一个重要作用就是调节系统输出量在数值上的数量级，使其相互之间有可比性.如果在性能指标中某个输出信号较其他信号更加重要，也将通过此加权函数来体现.在系统的频率响应中，对于输入干扰，输出信号会在某个频率范围内有较大的响应，而在其他频率范围内响应很小，可以忽略不计.所以，为了降低输入干扰的影响，只要减小输出信号在特定频率范围内的响应即可，即加权矩阵在此频率范围内将有较大幅值.

加权函数W的确定对于求解H∞问题非常关键，此通用飞机的气动弹性模型在连续阵风干扰下，输出信号有着不同的数量级，并且俯仰角和翼尖相对位移响应主要体现在低频域，而飞机质心加速度的响应主要在高频域.所以结合以上W函数选取原则，通过多次的调节，最终得到如下加权函数：

H∞的限制条件和求解方法由文献[16]给出.具体实践中借助MATLAB软件的Robust Toolbox工具箱[17]，得到控制器K.未加控制器的开环系统的性能指标‖Tzw‖∞=9.072，而对于闭环系统，‖Tzw‖∞=0.753.在MATLAB的Simulink中仿真得到阵风扰动下闭环系统的响应如图3所示，其中图3(a)为干扰阵风的波形图.

由图3可以看到，得到的H∞控制器对阵风干扰有很好的抑制效果.计算各输出信号在控制前后的均方根发现，闭环系统的输出信号俯仰角、翼尖相对位移和机身质心加速度相对于开环系统分别减小了87.3%，66%和23.7%.

4μ控制器设计

由H∞控制器得到的阵风缓和性能是对于标称系统而言的，即系统不存在不确定性.但是实际工程中的控制系统，由于种种原因总是存在不确定性.对于弹性飞机，各种不确定性因素更多、更复杂，包括结构阻尼的不精确、结构特性随时间的改变、未建模的高频特性、飞行过程中大气环境的改变等.考虑系统的不确定性后，需要通过μ综合方法分析系统的鲁棒性能，设计相应的控制器.

标准的μ综合分析框架如图4(a)所示.其中Δ满足‖Δ‖∞≤1，为未知摄动函数，描述了系统中存在的不确定性.μ综合方法的目标就是寻找一个能使系统稳定的控制器，并且使系统的结构奇异值满足：

(9)

这样，在对任意满足‖Δ‖∞≤1的未知摄动下，系统将能够保证鲁棒稳定性和鲁棒性能[18].目前(9)式还没有解析解法，主要通过D-K(Durand-Kerner)迭代法求解.

对于弹性飞机的阵风缓和控制问题，如图4(b)所示，这里加入频域内描述的乘性输入不确定性和输出不确定性.设G′(s)为系统G(s)从输入u到输出y的传递函数，则加入不确定性描述后得到：

其中： Δu和Δy分别为输入、输出摄动函数，且‖Δu‖∞<1，‖Δy‖∞<1；Wuncy和Wuncu为相应的不确定性加权函数.

不确定性加权函数的确定同样非常重要，一种关键的原则是尽可能减小模型的保守性，并使加权函数尽量不超过摄动的增益[1]，根据输入输出的不确定性程度选择加权函数为：

不确定性加权函数的bode图如图5所示，在低频域内系统输出含有4%的不确定性，副翼输入含有10%的不确定性，升降舵输入含有8%的不确定性，并且不确定性的大小随着频率的上升而变大，表征系统在高频不断增大的不确定性.

将Δ=diag(Δu,Δy)从图4(b)中隔离出来，实现系统的已知部分和未知部分分离，形成图4(a)所示的形式.借助MATLAB的Robust Toolbox工具箱，求解得到μ控制器，最终闭环系统的结构奇异值为 0.7218，满足(9)式，保证了闭环系统的鲁棒稳定性和鲁棒性能.通过Simulink仿真，系统在阵风干扰下，在存在输入输出不确定性的情况下，俯仰角、翼尖纵向相对位移和机身质心纵向加速度的均方根的值分别下降了72%、23%和16.2%.

把基于标称系统设计的H∞控制器加入到不确定性影响下的系统中发现，控制器已经不能保证闭环系统稳定.所以考虑系统不确定性的μ综合分析是非常有必要的.

5结语

本文结果表明对于弹性飞机标称模型，通过构建合理的分析框架和评价输出的加权函数，H∞控制方法给出了很好的阵风减缓性能.考虑到实际系统存在的不确定性，在包含输入输出不确定性模型的气动弹性模型上，μ综合方法给出了能同时保证系统鲁棒稳定性和鲁棒性能的控制器.文中构建的飞机气动弹性模型的计算流程具有通用型，可以用来分析一般结构外形飞机的气动弹性行为，得到的状态方程模型非常有利于飞机的控制问题研究.

虽然本文中构建的控制器在相应的气动弹性模型上都有着良好的性能表现，但是由于鲁棒控制方法的特点，设计出的控制器与开环系统的阶次在同一个数量级.气动弹性模型的高阶次导致了控制器的阶次相对很高，所以下一步的工作将集中在如何降低控制器的阶次，同时保证系统的性能下降不大.

参考文献：

[1]赵永辉.气动弹性力学与控制 [M].北京： 科学出版社, 2007.

[2]ALBANO E, RODDEN W P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows [J].AIAAJournal, 1969，7(2)： 279-285.

[3]RODDEN W P, GIESING J P, KALMAN T P. Refinement of the nonplanar aspects of the subsonic doublet-lattice lifting surface method [J].JournalofAircraft, 1972，9(1)： 69-73.

[4]KAPEL M. Design for active flutter suppression and gust alleviation using state-space aeroelastic modeling [J].JournalofAircraft, 1982,19(3)： 221-227.

[5]ZENG J, MOULIN B, CALLAFON R D,etal. Adaptive feedforward control for gust load alleviation [J].JournalofGuidance,Control,andDynamics, 2010,33(3)： 862-872.

[6]AOUF N, BOULET B, BOTEZ R.H2andH∞-optimal gust load alleviation for a flexible aircraft [C]. Chicago： American Control Conference, 2000： 1872-1876.

[7]COOK R G, PALACIOS R, GOULART P. Robust gust alleviation and stabilization of very flexible aircraft [J].AIAAJournal, 2013,51(2)： 330-340.

[8]AOUF N, BOULET B, BOTEZ R M. Robust gust load alleviation for a flexible aircraft [J].CanadianAeronauticsandSpaceJournal, 2000,46(3)： 131-139.

[9]ZONA Technology Inc. Version Z. 8.2 Theoreticalmanual [M]. Scottsdale, AZ： ZONA Technology Inc, 2008.

[10]MOULIN B, KARPEL M. Gust loads alleviation using special control surfaces [J].JournalofAircraft, 2007,44(1)： 17-25.

[11]ZONA Technology Inc. Version Z.8.2 user’s manual [M]. Scottsdale, AZ： ZONA Technology Inc, 2008.

[12]ROGER K L. Airplane math modeling methods for active control design [R]. AGARD-CP-228, 1977： 4.1-4.11.

[13]KARPEL M, MOULIN B, CHEN P C. Dynamic response of aeroservoelastic systems to gust excitation [J].JournalofAircraft, 2005,42(5)： 1264-1272.

[14]ZONA Technology Inc. Version Z.8.2 application’s manual [M]. Scottsdale, AZ： ZONA Technology Inc, 2008.

[15]纳尔逊,顾均晓.飞行稳定性和自动控制 [M].北京： 国防工业出版社,2008.

[16]ZHOU K, DOYLE J C, GLOVER K. Robust and optimal control [M]. New Jersey： Prentice Hall, 1996.

[17]BALAS G, CHIANG R, PACKARD A,etal. Robust control toolbox [M]. Massachusetts： The Math Works Inc, 2005.

[18]吴敏,桂卫华,何勇.现代鲁棒控制 [M].湖南： 中南大学出版社,2006.

文章编号：0427-7104(2016)03-0329-07

收稿日期：2015-05-29

作者简介：傅军(1990—)，男，硕士研究生，E-mail： 13210290011@fudan.edu.cn.

中图分类号：V 249.1

文献标志码：A

Robust Control of Flexible Aircraft for Gust Alleviation

FU Jun, WAN Jing, AI Jianliang

(DepartmentofAeronauticsandAstronautics,FudanUniversity,Shanghai200433,China)

Abstract：Gust disturbance has a serious impact on flight stability, performance and comfort for passengers. In this study, the design method of gust load alleviation controller for a flexible airplane is proposed. First, the general state-space equations of motion for an aeroelastic model in the longitudinal plane is built. Taking the Dryden gust model as the input, the nominal system H∞controller for the elastic aircraft is designed and achieves good gust alleviation effect. The RMS of the relative displacement of the tip and the centroid acceleration are reduced by 66% and 23.7%, respectively. Since the system in a real environment has a lot of uncertainty, the μ synthesis controller with the uncertain model is also designed. The simulation results show that the μ controller can achieve robust stability and robust performance for uncertainty systems, which is nearly impossible for the H∞controller.

Keywords：flexible aircraft; aeroelastic equation; gust load alleviation; robust control