浅谈隧道结构抗震设计方法

刘　根, 胡韵雪

(四川汶马高速公路有限责任公司, 四川成都 610041)



浅谈隧道结构抗震设计方法

刘根, 胡韵雪

(四川汶马高速公路有限责任公司, 四川成都 610041)

【摘要】穿越地震断裂带及地震活动频繁区的隧道及地下结构，在设计之初就应该对结构本身进行抗震设计，从而有效地降低或避免地震及断层活动对结构所造成的破坏。然而选择正确的抗震设计方法是隧道结构抗震设计的基础，对目前各类抗震设计方法的理论基础及适用范围的了解是进行抗震设计前必须开展的工作。

【关键词】隧道;震害；抗震;设计方法；拟静力法；有限元法

1隧道震害类型

1.1地震引起的震动破坏

最常见的地下工程震害有洞口滑坡、崩塌、地基砂土液化、地面沉降等导致洞口或洞口附近浅埋地段损坏，其次是地下工程扭曲变形、衬砌脱落、围岩松动以及由此导致的洞内崩塌、涌水、岩爆和诱发地震等次生灾害。以上震害又可分为两种类型，一种是由于围岩变位而在隧道结构中产生强制变形所引起的破坏，另一种是结构在地震惯性力作用下而产生的破坏。其中，第一种类型的破坏多数发生在岩性变化较大、断层破碎带、浅埋地段或隧道结构刚度远大于地层刚度的围岩之中，这是目前公认的主要破坏形式；第二种类型的破坏多数发生在洞口附近或浅埋地段，这时地震惯性力的作用表现的比较明显。

1.2断层活动造成的错动破坏

断层对地下工程的影响有两个方面：活动断层错动破坏和断层带破碎岩体在地震作用下发生塌落松动和涌水等。后者容易发现，可视为不良围岩进行加固处理；前者对工程危害最大，加固也最为复杂。

2地下结构抗震研究方法

地下结构震害的调查和理论分析发现，地下结构的地震反应大致有如下几个最重要也是最根本的特点：

(1)地下结构的振动变形受周围地基土体的约束作用显著，由于结构的表观密度和刚度都较小，所以结构本身的动力反应受自振特性影响很小，影响地下结构地震反应的主导因素是地基变形而不是地下结构的惯性力。

(2)地下结构在地震中受到的破坏比地面结构要轻，并且一般情况下埋深越大震害越轻。

(3)地下结构的存在对于周围地基地震反应的影响一般很小。

以这些特点为基础，存在着多种简化设计方法，在地下结构工程抗震设计中，较有代表性的方法有：地震系数法、不考虑相互作用的拟静力法、考虑相互作用的拟静力法和动力有限元法四种。

2.1地震系数法

地震系数法的思路是将随时间变化的地震力用等代的静地震荷载代替，再用静力计算模型分析地震荷载或强迫地层位移作用下的结构内力。

2.1.1结构横断面地震荷载计算

等代的静地震荷载包括结构本身的惯性力、洞顶上方土柱的惯性力以及主动侧向土压力增量。

主动侧向土压力的增量可以用物部-冈部法计算。结构的水平惯性力作用在构件或结构的重心处，表示为：

(1)

式中：a为作用于结构的地震加速度；g为重力加速度；Q为构件或结构的重量；Kc为与地震加速度有关的地震系数。

洞顶上方土柱的水平惯性力，由式(2)计算：

F2=hcKhmg

(2)

式中：hc为综合影响系数，与工程重要性、隧道埋深、地层特性等有关；Kh为水平地震系数；m为结构上方土柱的质量。

2.1.2沿隧道纵轴方向地震荷载的计算

地震动的横波与隧道纵轴斜交或正交，或地震动的纵波与隧道纵轴平行或斜交，都会沿隧道纵向产生水平惯性力，使结构发生纵向拉压变形，其中以横波产生的纵向水平惯性力为主。孙钧院士在《地下结构》中建议计算纵向水平惯性力时，对区间隧道可以按半个波长的结构重量考虑，即：

(3)

式中：hc为综合影响系数，与工程重要性、隧道埋深、地层特性等有关；Kh为水平地震系数；L为地震波横波波长；W为结构每1 m的重量。

地震系数法是我国目前工程设计中通用的方法，在设计时，一般把等效地震力并入静荷载中，在截面衬砌设计时一起考虑。但是此种方法是从应用于一般地上结构的地震系数法类比而来，不能反映地下结构地震反应的特点，在概念上存在根本性的错误。例如，根据公式(2)，作用在地下结构的水平惯性力随埋深而增加，这显然与震害的实际情况是不相符合的。

2.2不考虑相互作用的拟静力法

这种方法由Newmark等人在20世纪60年代提出，其忽略了地下结构和周围土介质因为刚度不同而在变形协调时所存在的相互作用，将地震波作用下自由场土介质的应变直接作为结构在地震作用下的反应变形进行计算。在概念上，这种方法反映了地下结构地震反应的主导因素是其周围地基反应这一根本特点，比地震系数法更为合理，在很多情况下可以给出地下结构地震反应应变的大致估计。此方法的结果一般作为考虑相互作用的拟静力法的理论基础，若要直接应用于设计实践，需要根据当地的地震环境和岩土介质特点进行简化。BART系统的抗震设计准则就是一个很好的例子，它包括抗震特点、变形限制、土体不连续影响、内部构件、附属构件、细部结构、土压力、临时结构等抗震设计内容。这种方法假定土体并不因地震作用而丧失其整体稳定性，地震作用只引起地下结构的振动效应。其震害机理是由于土体的地震变形而作用于地下结构产生的，从而使结构产生应力和位移，最终导致地下结构的破坏。BART法就是针对地下结构的破坏特点，提出了地下结构应具有吸收强变形的延性，并且不散失承受静载的能力，而不是抵御惯性力的新的地下结构抗震设计思想。

2.2.1地层的剪切变形

地铁结构设计过程中，必须考虑地铁结构变形能适应于土体的剪切变形。地层剪切变形的大小由下式确定:

(4)

式中：Ys/h为剪切变形角度；H为基岩以上的地层深度；V为土壤中剪切波的传播速度。

2.2.2地层的弯曲变形

地铁结构设计还需满足地层弯曲所强加的变形，结构的最大单元应变应根据波与地下结构斜交传播的情况得出。这种斜向传播的波包括一个产生弯曲变形的横向分量以及一个产生压缩膨胀变形和应变的纵向分量。

(5)

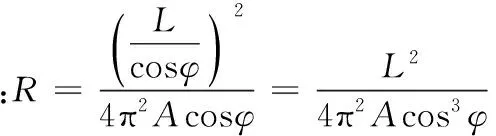
(6)

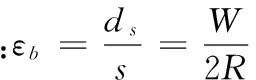
(7)

由斜向波产生的弯曲和拉伸应变之和为：

(8)

式中：A为正弦波的最大振幅；W为梁的厚度，取为L/6cosφ；εs为拉伸应变；εb为弯曲应变；φ为波的入射角；L为正弦波的波长；R为曲率半径。

通过以上各式计算得到地震引起的地层剪切变形和地层弯曲变形，使设计者能确定地震引起的地层振动特征，从而为地下结构的抗震设计提供理论依据。

2.3考虑相互作用的拟静力法

(1)反应位移法。这种方法的基本原理就是用弹性地基梁来模拟地下线状结构物，把地震时地基的位移当作已知条件作用在弹性地基上，以求解在梁上产生的应力和变形，从而计算地下结构(隧洞、管道、竖井等)地震反应，公式可以简化为拟静力计算公式K{U}=Ks{ug}。式中的矩阵K包括地下结构的刚度Kt和地基抗力Ks。本方法的关键是确定地震变位{ug}和抗力系数Ks，通常将Ks取为对角阵，则Ks相当于文克尔弹簧常数或地基土介质的弹簧常数。这种方法的理论基础是基于地震时地下结构反应分析的研究成果，即支配地下结构地震响应的是地基变形而不是结构物的惯性力，并首先将反应位移法用于沉埋隧道的抗震设计中。

(2)围岩应变传递法。根据地震波动场分析的基本思想以及管道、海底隧道、地下油库等的地震观测结果，表明地下结构地震时应变的波形与周围岩土介质地震应变波形几乎完全相似，因而可以建立关系式εs=aεg。式中：εs为地下结构的地震应变；εg为没有洞穴地下结构影响的周围岩土介质的地震应变；a为应变传递系数。可以把a看作是一个静态系数，它和地震动的频率和波长无关，只随地下结构的形状、刚度以及周围岩土的刚度而变化，可通过静力有限元法分析确定。其中关键的问题是确定与设计地震强度相符的围岩应变， 日本浜田政等人将地震波进行反演从地表面300m以下进行输入，剪切应变γyz由地震波的水平分量求得，上下方向正应变γzz按地震波的竖向分量推求，水平方向正应变γyy可模拟表面波的处理方法，将地震波水平分量产生的洞穴中心位置上的速度反应值除以围岩的P波波速得出。

(3)地基抗力系数法。这是将相互作用的计算模型应用于地下结构横断面地震反应分析的一种方法，可适用于埋设的地下结构。周围岩土介质的作用以多点压缩弹簧和剪切弹簧进行模拟，结构可用梁元素进行模拟。方法包括三个基本步骤：周围岩土介质弹簧常数的计算；围岩地震变位的计算；地下结构地震反应的计算。围岩抗力弹簧常数采用静力有限元法进行近似计算，围岩地震变位近似计算采用分段一维模型或平面有限元模型。

尽管以上三种方法求解方式略有不同，但基本原理和思路是一致的，有着共同的理论基础：(1)地下结构和周围土介质之间的相互作用以运动相互作用为主；(2)地下结构的存在对周围土介质的地震反应影响不大；(3)结构的应变与相应自由场土体分布相似、大小不同。

2.4动力有限元法

动力有限元方法可以模拟复杂边界条件，以及从初始应力场的形成直到结构在地震荷载下的破坏的全过程，其具有有很好的开放性，比较容易与其他相关的最新科学和技术相结合。如采用适当的材料本构模型，可以模拟结构和周围土介质在复杂荷载条件下的材料特性；采用适当的接触面模型或者接触算法，则可以模拟结构-土介质之间局部脱开、滑动、错位、张闭等非连续变形现象。由于动力有限元法的这些特点，它已经成为研究结构-土介质相互作用机理、揭示地铁地下结构地震灾变规律的强大工具。

3结束语

综上所述，现行的多种地下结构抗震设计方法，各有其优点和不足，分别适用于不同的情况，在实际的设计和研究中需要综合运用。各种设计方法比较见表1。

表1　各种设计方法比较

参考文献

[1]王秀英. 地下结构的震害类型及机理研究[J]. 中国安全科学学报， 2003(11)：57-58.

[2]林皋. 地下结构抗震分析综述(上)[J]. 世界地震工程, 1990 (2)：1-10.

[3]林皋. 地下结构抗震分析综述(下)[J]. 世界地震工程, 1990 (3)：1-10.

[4]Hamada H, Kitahara M. Earthquake observation and BIE analysis on dynamic behavior of rock cavern. Numerical Methods in Geomechanics. Preoceedings of the Fifth International Conference on Numerical Methods in Geomechanics. Nagoya 1-5 APRIL 1985: 1525-1532.

[5]陈贵红. 沉管隧道抗震数值分析[D]. 西南交通大学， 2002.

[作者简介]刘根(1983～)，男，工学硕士，工程师，从事高速公路建设管理等相关工作。

【中图分类号】U452.2+5

【文献标志码】A

[定稿日期]2015-11-26