基于数值仿真和岩土特性的反演方法

王　琛， 张金柱

(北京城建设计发展集团股份有限公司, 北京 100025))



基于数值仿真和岩土特性的反演方法

王琛， 张金柱

(北京城建设计发展集团股份有限公司, 北京 100025))

【摘要】文章通过以数值仿真作为参数反演工具，以岩土参数对环境变形的影响模式和参数测试数据的离散性作为反演分析基础，建立了基于数值仿真和岩土特性的反演方法，并初步实现了该方法。实例表明，该方法具有较强的实用性，为工程反演提供了一种新思路。

【关键词】参数反演;数值仿真;岩土特性

地铁等地下工程要求进行信息化设计和施工，根据施工监测结果修正设计，其重点和难点是参数反演。目前，工程反演方法主要有逆解法、直接法、图谱法和智能反演法[1-4]。逆解法中由正分析方程反推得到逆方程，利用量测位移得到待定参数；直接法中把参数反演问题转化为一个目标函数的寻优问题，直接利用正分析的过程和格式，通过迭代最小误差函数，逐次修正未知参数的试算值，直至获得“最佳值”；图谱法中以预先通过由数值计算得到的对应于各种不同弹性模量和初始地应力与位移的关系曲线，建立简便的图谱和图表，并根据相似原理，由现场量测位移通过图谱和图表的图解反推初始地应力和弹性模量，智能反演法是一种源于自然进化的全局搜索优化算法，与直接法相近，只是求解速度有所提高。这些方法是参数反演研究的优秀成果，但也存在不足之处。逆解法要求输入和输出之间有明确的函数关系，直接法和智能反演法计算工作量大，解的稳定性差，图谱法过于依赖地区经验。

本文在上述成果的基础上，以数值仿真作为反演工具，以岩土参数对环境变形的影响模式和参数测试数据的离散性作为反演基础，建立了基于数值仿真和岩土特性的反演方法。该方法为岩土工程参数反演提供了一条新思路，对于参数反演的理论研究和工程应用都具有一定的参考价值。

1本文反演方法综述

1.1基本思想

(1)基于数值仿真建立岩土参数和环境变形之间的正向映射关系。即根据岩土参数数值计算得到环境变形。假定参数合理时，数值计算结果基本正确。

(2)基于岩土参数对变形的影响模式建立岩土参数和环境位移之间的反向映射关系。即根据正向映射关系归纳出参数对变形的影响模式，具体到个案工程反演中调整参数少量试算来标定影响模式中的系数，以得到针对个案工程的影响关系式。把现场监测的环境位移结果代入上述关系式，就可以求得参数的反演值。

(3)基于岩土参数测试数据的离散性确定参数优化的合理区间。通过对大样本测试数据的统计，能够得到参数真实值的分布区间，即离散区间。对于反演得到的参数，如果落于离散区间之内，则取该值作为反演值；如果小于离散下界，则取离散下界值作为反演值。反之亦然。

1.2反演步骤

本文方法分前期研究和个案反演两个阶段。在前期研究阶段需要开发参数反演中使用的数值仿真程序，分析岩土参数对环境变形的影响模式以及分析参数的离散性。具体到个案工程的参数反演中，反演的主要操作步骤如下，其流程如图1所示。

(1)根据所反演的参数对环境变形的影响模式，确定反演分析的最少试算组。例如，某一参数以三次多项式规律影响环境变形，则反演分析中至少需要试算四组来标定影响关系式；

(2)根据按参考值的计算结果与监测结果的比较，确定参数反演计算方案中参数的调整趋势。例如，按参考值计算的变形小于监测结果，则参数应该向减小环境变形的方向调整，使反演参数是通过内插求得，而不是外延求得；

(3)根据反演参数的离散性分析结果，确定参数的合理反演区间；

(4)根据上述三项制定计算方案；

(5)按计算方案计算，并回归建立针对本工程的反演参数与环境变形之间的定量关系式；

(6)根据监测数据与计算结果之间的关系，建立反演优化的目标函数；

(7)根据目标函数全局最优原则得到反演参数的优化值；

(8)判断反演优化值是否合理。如果反演优化值落于反演区间之内，表明结果合理，该优化值就是反演结果；如果优化值落于反演区间以外(如大于反演上界)，表明结果不合理，以反演区间边界(如上界)作为反演结果；反演结束。

图1　参数反演流程

2数值仿真技术

数值仿真方法作为本文参数反演的工具，主要有有限差分法、有限元法、离散元法等。目前岩土工程数值仿真分析日趋成熟，但大都是由专业人员进行专题分析，计算周期较长，普及率较低。本文反演方法中要求在短时间内进行多次数值计算，现有计算软件无法满足。笔者以EXCEL数据库和FLAC3D[5]及其fish语言作为开发平台，探索开发了土钉支护边坡数值仿真模块建模程序，图2是参数输入界面，图3是生成的计算模型。该方法中以EXCEL数据表和工程性语言的形式输入参数，其会自动转换并生成FLAC3D模型。该程序适用于土钉道数≤20，土层数≤10，坡度等其他参数不限。该方法解决了建模问题，一次建模时间不超过10 min，建模效率较高。但计算核心为FLAC3D程序，计算时间较长，数值仿真普遍存在的计算耗时的问题还需要更多的学者共同努力解决。笔者认为，随着计算技术的不断发展，尤其是计算机硬件的不断提高，数值计算时间长的问题能够得到有效解决。

图2　参数输入界面

图3　土钉墙模型

3岩土参数对环境变形的影响模式

岩土参数对环境变形的影响模式是本文参数反演方法的理论基础之一，这里采用实例的方式来阐述其实现过程。

利用本文第2节提及的土钉支护基坑模块建模程序来分析土体变形模量对土钉墙顶水平位移和垂直位移的影响模式。选取文献[6]中介绍的丽水嘉园基坑工程作为分析实例，文献中提供的参数值(勘察数据)作为基准状态参数值(表1)。在基准参数值的基础上按比例调整参数，通过数值计算得到基坑位移的变化结果。从参数值的实际可能变化范围考虑，参数在参考值的基础上上下浮动20%和40%，计算得到变形模量变化时的5组环境变形，调整后的参数及其计算结果如表2所示，环境位移随变形模量调整系数变化的曲线如图4所示。结果表明，变形模量与土钉墙位移之间的关系基本符合三次多项式关系模式。

其中，三次多项式1为：

y=92.292x3-356.39x2+485.54x-260.86

三次多项式2为：

y=99.063x3-393.28x2+550.58x-306.85

表1　基准状态参数值

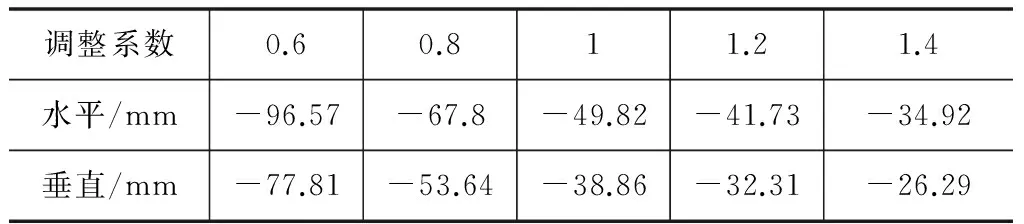
表2　坡顶位移计算结果

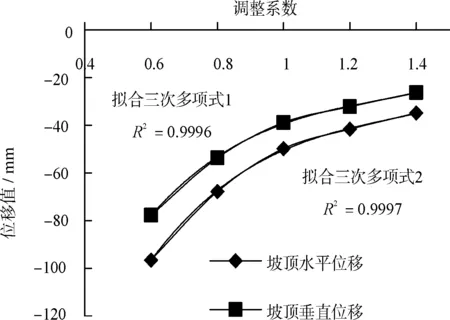
图4　变形模量-位移关系曲线

4岩土测试数据的离散性分析

4.1分析方法

岩土测试数据的离散性是本文反演方法理论基础之二。工程中最主要的岩土测试数据是地质勘察数据，其为设计的最主要依据，但是岩土勘察数据是不够准确的，原因主要有：(1)土体在空间上不均匀，而钻孔空间离散且数量有限，因此钻孔资料不能准确描述全部的地层参数。(2)土体是由颗粒组成的弹塑性材料，其物理力学性能与应力历史、应力状态和应力路径有关，土工试验会对土体产生扰动，导致应力环境发生改变。(3)土工试验仪器不够精密，人员操作也往往会带来误差。

从上面分析可知，岩土参数勘查数据的不准确性由多个因素造成，对每个影响因素都深入研究清楚固然最理想，但很难实现。退而求其次，这里从宏观上进行统计分析。在地勘报告中，一项指标通常包括测试样本数、最大值、最小值、平均值等。这些数值都体现了测试结果的离散分布特性，也体现了岩土参数真实值可能出现的范围和概率。对于大样本，统计结果能够确定参数真实值所在的区间。

为了对勘察数据的离散性进行量化分析，这里假设某一参数a，勘察试验样本数为N，最大测试结果为amax，最小测试结果为amin，测试结果平均值为aav。定义：相对最大值ρmax=最大值amax/平均值aav≥1，相对最小值ρmin=最小值amin/平均值aav≤1，相对平均值ρmin=平均值aav/平均值aav=1。例如对于压缩模量，计算每组数据的ρmax，统计ρmax在区间[1+Δn，1+Δ(n+1) )内的出现的频次(Δ为统计步长，n=0,1,2,3…)。按区间从小到大顺序对出现的频次进行累加，得到累积出现频次。用累积出现频次除以统计样本数，就得到累积概率密度。定义累积概率密度的超越概率为5%时对应的区间点值为离散上界ρmax95。同理，可以对岩土参数项进行离散下界分析。定义离散区间为[ρmin95,ρmax95]。本文中暂取离散界限对应的超越概率为5%，该值应该根据更深入的研究确定。

4.2岩土勘察数据的离散性分析的分析实例

本文收集了北京、深圳、天津、成都、青岛、合肥6市19个工程87层土的岩土勘察数据，通过第4.1节中的分析方法对结果进行统计(表3)。

表3　压缩模量统计结果

离散下界通过离散小值的统计得到，统计区间取[1-0.02n，1-0.02(n+1) )(n=0,1,2,3…，Δ=0.02)，结果如表3所示。同理，离散上界通过离散大值统计得到，取统计区间为[1+0.1n，1+0.1(n+1) )(n=0,1,2,3…，Δ=0.1)。鉴于篇幅，具体数据不再赘述。

根据上述统计得到的累积概率密度在统计区间内的分布，绘制累积概率密度分布曲线如图5所示。从图中可知，超越概率为5%的离散区间为[0.564，1.641]，即表明压缩模量真实值与勘察值的比为0.564～1.641的可能性为95%。所以在压缩模量反演中，可认为当反演值与勘察值的比值落于[0.564，1.641]之内时是合理的，落于之外时是不合理的，取相应的边界值。

图5　累积概率密度曲线

由于笔者收集到的岩土勘察数据的局限性，这里的分析结果是不够理想的。笔者认为，岩土测试数据的离散性分析应该分地域、土性、测试方法进行分类统计，这有待于后续深入研究。

5应用实例

5.1实例概况

取文献[6]中介绍的丽水嘉园土钉支护基坑工程作为反演算例。该工程在文献中给出的岩土参数作为参考值，利用参考值计算坡顶水平位移和垂直位移，在该位移值的基础上增加5%作为目标位移来模拟实测位移值，目标位移值如表4所示。

表4　目标位移值

5.2反演过程

根据本文第3节研究结果，变形模量变化与土钉支护边坡的位移基本符合三次多项式关系模式，所以本部分反演计算中取4组数据试算。根据本文第4.2节中对压缩模量(压缩模量与变形模量规律一致)勘察结果的统计分析，离散区间为[0.564，1.641]，同时考虑目标位移值比参考位移值大，即变形模量反演值应该比参考值小，所以调整参数取0.6、0.8、1.0和1.2进行试算，计算结果如表5所示。

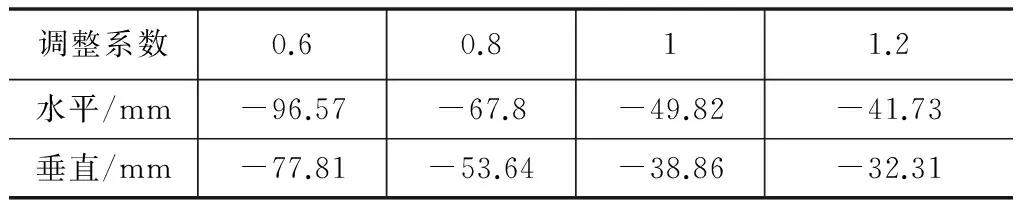
表5　位移试算结果

对表5中数据进行三次曲线拟合，得到变形模量调整系数和坡顶水平位移的关系式为：

Wh=18.75t3-179.88t2+367.93t-256.62

变形模量调整系数和坡顶垂直位移的关系式为：

Wh=24.16t3-175.38t2+330.61t-218.26

建立反演优化目标函数为：

F[Eopt]=min{(wh(E)-wh)2+(wv(E)-wv)2}

根据上述拟合关系式与上述目标函数，计算得到当水平位移差和垂直位移差平方和最小时，变形模量调整系数为0.965。

5.3反演结果合理性判断及结果验证

根据本文第4.2节统计结果，压缩模量超越概率为5%的离散区间为[0.564，1.641]，本节参数反演调整系数为0.965，处于离散区间之内，因此认为是合理的。

将参考变形模量参数值乘以0.965便是反演得到的变形模量值，结果如表6所示。

表6　变形模量反演值

对上述得到的反演值进行验证计算，结果如表7所示。结果表明，计算值与目标值之间相差较小。

表7　目标值与反演值比较

6结论

本文提出的基于数值仿真和岩土特性的参数反演方法为工程反分析提供了一种新的思路，具有以下优点：

(1)以数值仿真作为工具，以岩土特性作为基础，该方法具有较强的理论依据和可操作性。

(2)本文中的参数对环境变形的影响，在前期研究阶段确定模式，在个案分析中标定关系式，因此得到的关系式更具针对性，能够更好的考虑岩土参数的普遍性和具体工程的特殊性。

(3)以勘察数据的离散性来判断反演值是否合理，简单易行，意义明确。

本文反演方法具有很好的发展前景，但其中的数值仿真技术、岩土参数对环境变形的影响规律及岩土测试数据的离散性需要进行更加深入的研究。

参考文献

[1]Sakurai S , Abe S. A design approach to dimensioningunde-rground openings [A] . In : Proc 3rd Int Conf Numerical Methods in Geomechanics[C] .Aachen ,1979： 649-661.

[2]Sakurai ,S ,Takeuchi K.Back analysis of measured displacementof tunnel [J] . Rock Mech and Rock Eng ,1983 ,16 (3) :173-180.

[3]Gioda G, Pandolfi A ,Cividini A. A comparative evaluation ofsome back analysis algorithms and their application to in2situload tests[A]. In :Proc 2nd Int Symp on Field Measurement inGeom[C] . Kobe ,1987： 1131-1144.

[4]杨志法. 有限元法图谱[M] . 北京:科学出版社,1988.

[5]ITASCA 软件公司. FLAC程序用户使用手册[Z].

[6]段启伟.土钉支护现场实测与数值模拟[D]. 北京交通大学,2007.

[作者简介]王琛(1978～)，男，本科，工程师，主要从事地铁等地下结构的设计和研究工作。

【中图分类号】TU441+.3

【文献标志码】A

[定稿日期]2015-10-12