飑线组织化过程对环境垂直风切变和水汽的响应

张建军王咏青钟玮1湖南省气候中心，长沙410118南京信息工程大学大气科学学院太平洋台风研究中心，南京100443解放军理工大学气象海洋学院，南京111014南京大学中尺度灾害性天气教育部重点实验室，南京10093



飑线组织化过程对环境垂直风切变和水汽的响应

张建军1, 2王咏青2钟玮3, 4
1湖南省气候中心，长沙410118
2南京信息工程大学大气科学学院太平洋台风研究中心，南京210044
3解放军理工大学气象海洋学院，南京211101
4南京大学中尺度灾害性天气教育部重点实验室，南京210093

摘 要利用ARPS模式对飑线发生发展过程进行二维理想数值试验，讨论了低层环境垂直风切变和水汽条件变化时，飑线内部物理因子配置变化及其与系统强度演变的联系。研究表明，飑线发展过程中出现的动量、热量和水汽的再分配过程，造成系统内垂直环流结构和扰动温湿场分布发生变化，从而影响系统内部深对流的组织化过程和飑线强度的发展。基于低层环境垂直风切变和水汽两个要素的敏感性试验研究表明，低层环境垂直风切变增大（减小）时，飑线移速减慢（加快），冷池前沿激发的新对流与中高层的垂直运动相互贯通（分离），飑线系统强度随之增强（减弱）。此外，当低层水汽增加（减少）时，会导致输送到中层的水汽增加（减少），中层凝结潜热释放增多（减少），该层垂直运动增强（减弱）；同时，飑线系统区域环境释放的对流有效位能（CAPE）增大（减小），新生对流的强度增强（减弱）。低层水汽条件通过水汽输送和能量释放，改变冷池前沿新对流与中高层垂直环流的组织化结构，从而影响飑线强度。

关键词飑线 数值模拟 冷池 环境垂直风切变 水汽1

张建军, 王咏青, 钟玮. 2016. 飑线组织化过程对环境垂直风切变和水汽的响应 [J]. 大气科学, 40 (4): 689–702. Zhang Jianjun, Wang Yongqing, Zhong Wei. 2016. Impact of vertical wind shear and moisture on the organization of squall lines [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40 (4): 689–702, doi:10.3878/j.issn.1006-9895.1505.14337.

1 引言

飑线是有组织的雷暴群带状排列形成的中尺度对流系统，往往伴随有局地暴雨、短时大风、冰雹等强灾害性的强对流天气，维持时间有时能够达到或超过十几小时。对于这类有较长生命史的灾害性天气现象，探讨其在不同环境条件下的发展变化过程对防灾减灾具有重要作用。

早在20世纪50年代，Newton（1950）指出水平风速存在垂直切变的条件下，低层辐合高层辐散的配置有利于雷暴的维持和发展。后续研究表明垂直于飑线的环境垂直风切变是飑线发展演变的关键因子（Fujita, 1955）。统计资料也显示大多数飑线的环境垂直风切变与飑线正交（Bluestein and Jain, 1985; Bluestein et al., 1987; Wyss and Emanuel, 1988）。近三十年来，飑线的强对流运动被认为是冷池与低层（0～2.5 km）环境垂直风切变相互作用的结果更是得到了广泛认可（Thorpe et al., 1982; Rotunno et al., 1988；Weisman and Rotunno, 2004; Takemi, 2006, 2007, 2014; Coniglio et al., 2012；陈明轩和王迎春，2012）。其中Rotunno et al. (1988) 提出的理论被称之为RKW理论，RKW理论认为低层环境垂直风切变与近地面冷池强度相当时，飑线强度最强，两者相差较大时则飑线减弱。

除了低层环境垂直风切变对飑线的发展维持至关重要外，其他环境因子的作用也不容忽视。Takemi（2006）指出在较湿的环境下，更强的切变更有利于强对流的发展，且保持环境中水汽总量一致，低层更湿的环境所生成的飑线强度会更强。Takemi（2007）还指出在对流不稳定层中，静力稳定度在决定飑线强度方面起着重要作用；在相同静力稳定度环境下，对流有效位能（CAPE）及可降水量能有效的表示飑线强度。Parker（2008）通过不断减小近地面层的温度使得飑线所处环境的温度要素不断发生变化，并探讨了这种条件下飑线的发展变化过程。

以往的理想数值试验及个例分析，研究了环境垂直风切变、水汽等环境要素在特定配置条件下，飑线触发和组织化的物理过程，并通过冷池强度与环境垂直风切变的比值（简称为冷切比）来解释飑线发展变化的原因，并未从飑线内部环流结构的变化出发来探讨飑线强度变化的机理。实际上在飑线发展演变过程中，系统内部出现了动量、热量和水汽的输送、集中等再分配过程，并依此对飑线组织化程度产生影响。本文通过理想数值试验，研究适宜环境配置条件下，飑线触发和发展阶段系统内部动量、热量和水汽的再分配过程，及其对飑线系统强度变化的影响，并在此基础上讨论当低层环境垂直风切变和水汽等环境要素场发生变化时，系统内部各物理因子的响应过程及其对飑线系统强度变化的影响。文章第二部分基于RKW理论最优环境条件配置模拟了飑线的发生发展过程，深入分析了系统内部动量、热量和水汽的再分配过程及其与飑线系统强度变化之间的联系；第三、四部分则分别介绍飑线发展过程中其强度对低层环境垂直风切变和低层水汽的响应结果，并通过分析飑线的内部环流结构探讨了飑线强度变化的原因；最后对本文进行了归纳总结。

2 飑线触发及发展过程的数值试验

观测研究表明，飑线具有明显的准二维特征，即沿飑线方向上各个风暴单体的发展演变特征比较相似（Thorpe et al., 1982; Fovell and Ogura, 1988; Houze et al., 1989; Parker, 1998; Parker and Johnson, 2004），因此本文采用Xue et al.（2000）开发的非静力风暴尺度高级区域预报系统（ARPS）模式（5.3.4版本），设计了二维理想数值试验，再现飑线的触发和发展过程，以及飑线发展过程中系统内部物理量再分配的物理图像。

2.1 试验设计

假定理想二维剖面为x–z平面，水平（x）方向区域为360 km，分辨率为600 m；垂直（z）高度为18 km，为尽可能节省计算时间并模拟出精细的飑线低层垂直结构，垂直方向上进行了网格拉伸，即在z=3 km以下格距固定为100 m，3～15 km高度上则采用双曲正切函数拉伸，最大格距为574 m，15 km以上格距都为574 m。这样的分辨率已足以模拟出飑线的结构及其组织化过程（Weisman and Rotunno, 2004）。模式顶层及底层为刚性边界，水平方向上为开放边界。为了减小模式顶层向下反射的影响，14 km高度以上开启了瑞利阻尼选项（Takemi, 2006）。

试验中温湿背景场参考了Weisman and Klemp （1982）所设计的理想探空曲线（图1），其计算公式如下：

其中，对流层顶高度 ztr=12 km，对流层顶处的温度Ttr=213 K，对流层顶处的位温θtr=343 K；θ0表示地面位温，恒定为300 K；g为重力加速度；cp为干空气比定压热容；q(z)为基态位温；r为相对湿度。混合层的高度设置为1.2 km，在混合层中相对湿度最大值为0.95，依据RKW理想试验的最优配置，我们将对照试验的最底层比湿设置为 qv=14 g kg−1，垂直切变在垂直方向上的范围为0～2.5 km，水平风速自地面至 2.5 km高度的变化值（Us）为17 m s−1，即地面风速为−17 m s−1，线性增强至2.5 km处，以上风速都为0 m s−1。

对照试验初始对流启动采用的是热泡激发方案，即给定一个中心位于模式底层x=90 km处（将此处设为零点），水平半径为 10 km，垂直半径为2.5 km的热泡，初始扰动位温在中心点处设定为2 K，并按余弦函数向半径范围内递减，范围以外则都为零。模拟采用了冰微物理过程（Lin et al., 1983）。此外，试验没有考虑锋、急流等飑线环境，也忽略了科氏力的影响。模式资料每 10分钟输出一次。

2.2 飑线触发试验结果

理论研究（Thorpe et al., 1982; Rotunno et al., 1988）和敏感性试验（图略）均表明：对照试验的这种环境配置条件，能够使得对流触发过程所能达到的最旺盛阶段维持时间最长，强度最大。图2给出了系统触发过程不同发展阶段的内部环流结构、扰动位温和扰动比湿的垂直剖面图。积分1.5 h时（图 2a），飑线处于初步形成阶段，在热泡的中心点（x=0 km）处存在伸展高度接近6 km的垂直上升运动带，对流层高层（8 km）处出现了以x=0 km为中心向正负两个方向的辐散气流；由于上升气流不断地将低层水汽输送到中层，使得上升带中扰动比湿为正值，同时凝结作用产生的大量潜热也使得上升带3～5 km高度上出现明显的扰动增温；上升气流左侧存在的明显下沉运动，一方面使得凝结的水汽下落形成降水，另一方面将高层较为干冷的空气向下输送，并在低层环境风影响下向水平负方向扩散，造成热泡中心左侧大片2 km高度以下的区域出现了负的扰动比湿，同时1 km以下出现大面积扰动降温，说明对流启动后，在降水和干冷空气下传堆积的影响下，冷池开始形成。

飑线进一步发展后系统内部结构出现明显变化（图2b）：首先由于近地面位温以及比湿的扰动降幅增大，冷池强度增强，地面冷池前沿移动至x=6 km处，且其后部水平风速明显减弱，表明冷池增强后干冷空气质量堆积产生的外流逐步削弱了近地面层基本环境气流的影响；其次虽然冷池前沿的右移使得地面强迫上升的启动位置随之右移，但对流层中层上升运动和潜热释放的大值中心与地面冷池前沿的水平位置相差不大，因此对流层中层上升运动区的局地增温，以及高空辐散外流的抽气和通风效应，与地面冷池强迫垂直贯通，有利于垂直环流的进一步增强，同时这种垂直方向贯通的倾斜对流使得飑线系统上升运动和下沉运动分离，也有利于飑线系统的组织化和其后部降水增强。在飑线维持阶段（图 2c、2d），由于累积降水的不断增加使得冷池强度进一步加强，在冷空气堆质量辐散的强大作用下，2 km高度以下扰动位温负值覆盖区域水平风速开始出现逆基本气流的分布特征，因此地面冷池前沿及其引起的地面强迫上升的起始位置开始快速向右推进。在此影响下，系统的环流结构出现明显的倾斜状态，对流层中层上升运动以及凝结和高空辐散造成扰动增温的大值中心均明显落后于低层，这种垂直分布导致中高层凝结和辐散引起的对流运动与地面冷池造成的强迫抬升难以形成有效的连通。到积分6.0～6.5 h时（图2e、2f），这一现象尤其明显，因此图2e、2f中虽然地面降温、地面上升速度和中高层扰动增温相比前一阶段（图2c、2d）在量值上均增大，系统强度却开始减弱。

以上分析表明，飑线的发展伴随着系统内部垂直环流以及冷池强度的变化，冷池发展到一定强度后，不仅对飑线内部结构产生影响，还能够通过与环境垂直风切变等环境因素共同作用，对飑线的组织化和维持具有重要影响（RKW理论）。为了定量描述飑线不同阶段冷池的强度、结构和演变过程，本文对飑线发展过程中的冷池强度进行定量计算。RKW理论给出的单点冷池强度（C）定义公式为

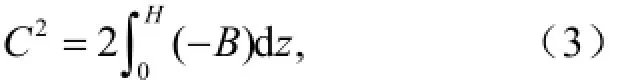
其中，H为冷池的高度，B则表示浮力，具体定义如下：

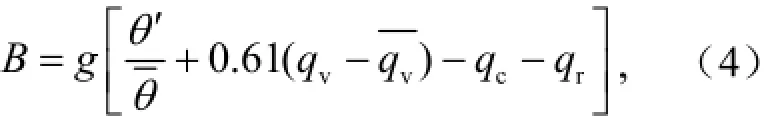
由图2分析可知，冷池的形成和发展均出现在地面上升运动后部的大片区域中，在垂直方向上也存在伸展，单点强度很难准确描述冷池的发展过程，需要对其垂直高度和水平覆盖范围进行界定。

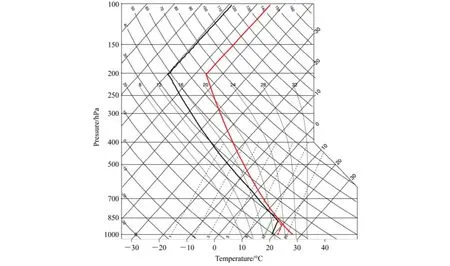
图1 三种比湿条件下的Skew-T图。其中绿色点线、黑色实线、红色虚线分别为12 g kg−1、14 g kg−1、16 g kg−1条件下的露点曲线，红色实线为温度曲线Fig. 1 Diagram of Skew-T under three specific humidity used in the numerical simulations. The green dotted line (qv= 12 g kg−1), black solid line (qv= 14 g kg−1), and red dashed line (qv= 16g kg−1) are dew point curves, the red solid line is temperature curve

v在实际计算中，冷池的垂直高度H边界取扰动位温自底层向上递增至−1 K时的高度（Takemi, 2006）；考虑到冷池的快速水平扩散及其对飑线系统的影响，采用Takemi（2007）和Parker（2008）的方法，选取地面冷池前沿线至其后部20 km范围作为冷池强度计算的水平区域。综上讨论，本文在计算过程中，取界定区域内冷池强度的平均值作为系统的冷池强度。需要说明的是，本文设定的冷池前沿线为扰动位温梯度最大值处。

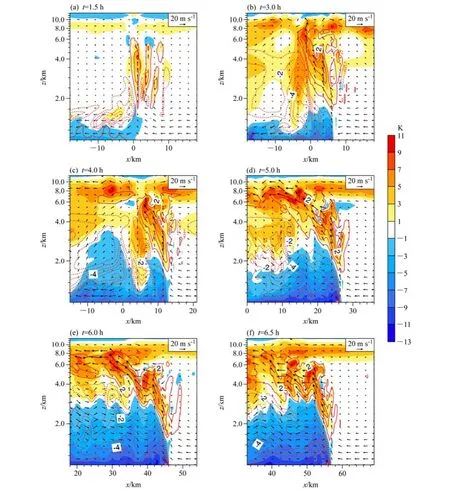
图2 对照试验不同发展阶段的垂直剖面图。阴影为扰动位温（单位：K），红色等值线为扰动比湿（间隔：1.0 g kg−1，未绘制零线），箭头表示风场（单位：m s−1）。横坐标为水平距离，零点为热泡中心点，纵坐标为垂直距离Fig. 2 Vertical cross sections of control simulation in different stages of development. Color scales represent perturbation potential temperature (units: K), red contours represent perturbation specific humidity (interval: 1.0 g kg−1; zero line not plotted), and arrows represent wind field (units: m s−1). The x-axis is horizontal distance, the point of zero represent the center of thermal bubble, and the vertical axis is vertical distance

为更具体的说明飑线强度与冷池强度之间的联系，图3给出了积分9 h内5 km高度上的垂直运动、地面降温以及冷切比。由于Us始终为17 m s−1，因此冷切比与冷池强度等价。由图分析可知，积分初始0.7 h内，整个模拟区域在5 km高度上垂直速度均小于4 m s−1，说明此时对流强度较弱，地面扰动位温大于−1 K，冷池强度基本为零。积分0.7 h后，垂直运动增强并开始出现超过4 m s−1的上升运动大值中心，其位置基本位于x=0 km处，且大值中心在时间—空间的二维平面上呈现连续分布的状态，说明该区域开始出现强度较强且伸展高度较高的深厚对流，并且这类深厚对流在该区域能够稳定地激发和维持，组织化的飑线系统开始形成；同时地面也出现小于−1 K的扰动位温，冷池前沿的位置与系统上升运动大值中心位置一致，计算得到冷池强度在半小时内快速增强，冷切比达到0.65左右后稳定持续至2.5 h。随后，冷池强度进入了近2个小时的持续快速增长期，到积分4.5 h时冷切比超过 1.5，此时上升运动大值区不仅在时间和强度上保持连续发展的态势，水平范围也明显扩大；地面扰动位温减小进一步加剧，冷池前沿线开始出现较为明显的向前移动，5 km高度上升运动中心稍落后于冷池前沿，但两者水平距离较小。随后到积分6 h时间段内，虽然冷切比仍呈现较为平缓的增大趋势，但是上升运动大值中心的分布呈现强度减弱，结构不连续的特征，说明飑线强度开始减弱。同时冷池前沿随时间快速向x正方向推进，且逐渐远离上升运动中心；到积分6 h后，冷切比维持在 2.2左右，地面出现超过−13 K的降温中心，但5 km高度上的上升运动结构零散，强度迅速减弱直至消失。Weisman和Rotunno（2004）指出当冷切比介于1.0～1.5时，最适宜飑线的发展，从上述分析来看本文结果与其一致。

由此可见，在RKW理论最优配置条件下，飑线系统经历了从对流启动到深对流组织化，最后减弱消散的演变过程。在这一过程中，冷池强度的变化与飑线强度有很好的对应关系，这与RKW理论结果一致，与此同时系统内部位温、比湿以及风场发生了显著的变化，即动量、热量以及水汽出现区域性的再分配，与之相对应的则是系统内部环流结构发生改变，并依此对飑线的组织化程度产生影响。接下来，我们将在飑线发展过程中改变低层环境垂直风切变或水汽，探讨这种情形下系统内部各物理因子的响应过程及其对飑线系统强度变化的影响。

3 低层环境垂直风切变的变化对飑线强度的影响

从对照试验可以看出，对流发展及其伴随的降水过程会使得冷池强度持续增强，与此同时，整体环境风的垂直切变变化却并不明显，即冷切比不断增大。因此，依据RKW理论及Weisman and Rotunno （2004）结果，冷切比介于1～1.5时飑线强度最强，随着冷切比的持续增加，飑线强度开始减弱。而环境垂直风切变是影响冷切比的关键因子，因此本节将低层环境垂直风切变作为敏感性因子，探讨在切变改变的条件下飑线强度如何变化，并从飑线系统的内部环流结构出发解释这一强度变化原因。

对照试验结果表明2.5～4.5 h这一阶段是飑线发展最强盛的阶段，随后垂直运动减弱，因此我们选取了对照试验积分3 h这一积分时刻的飑线状态作为敏感性试验的初始对流，之后飑线所处环境相较对照试验发生变化（指垂直风切变或水汽），其他配置则与对照试验相同。环境垂直风切变只考虑低层切变一种类型（0～2.5 km），但设计了三种不同大小的Us值，即14 m s−1，17 m s−1，20 m s−1。各试验命名见表1。

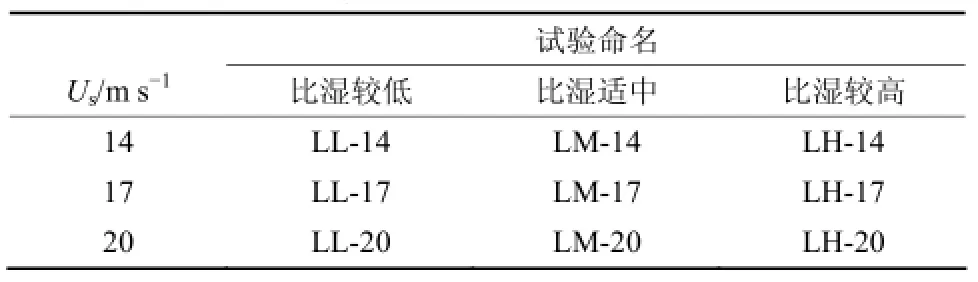
表1 各试验命名。其中，第一个字符L表示低层切变，第二个字符L、M、H分别表示低层比湿较低（qv=12 g kg−1）、适中（qv=14 g kg−1）、较高（qv=16g kg−1）Table 1 Details of the experiments, in which the first character L represents the low level shear, the second characters L, M, and H represent the lower (qv=12 g kg−1), moderate (qv=14 g kg−1), and higher (qv=16 g kg−1) specific humidity, respectively

3.1 飑线强度对低层环境垂直风切变的响应

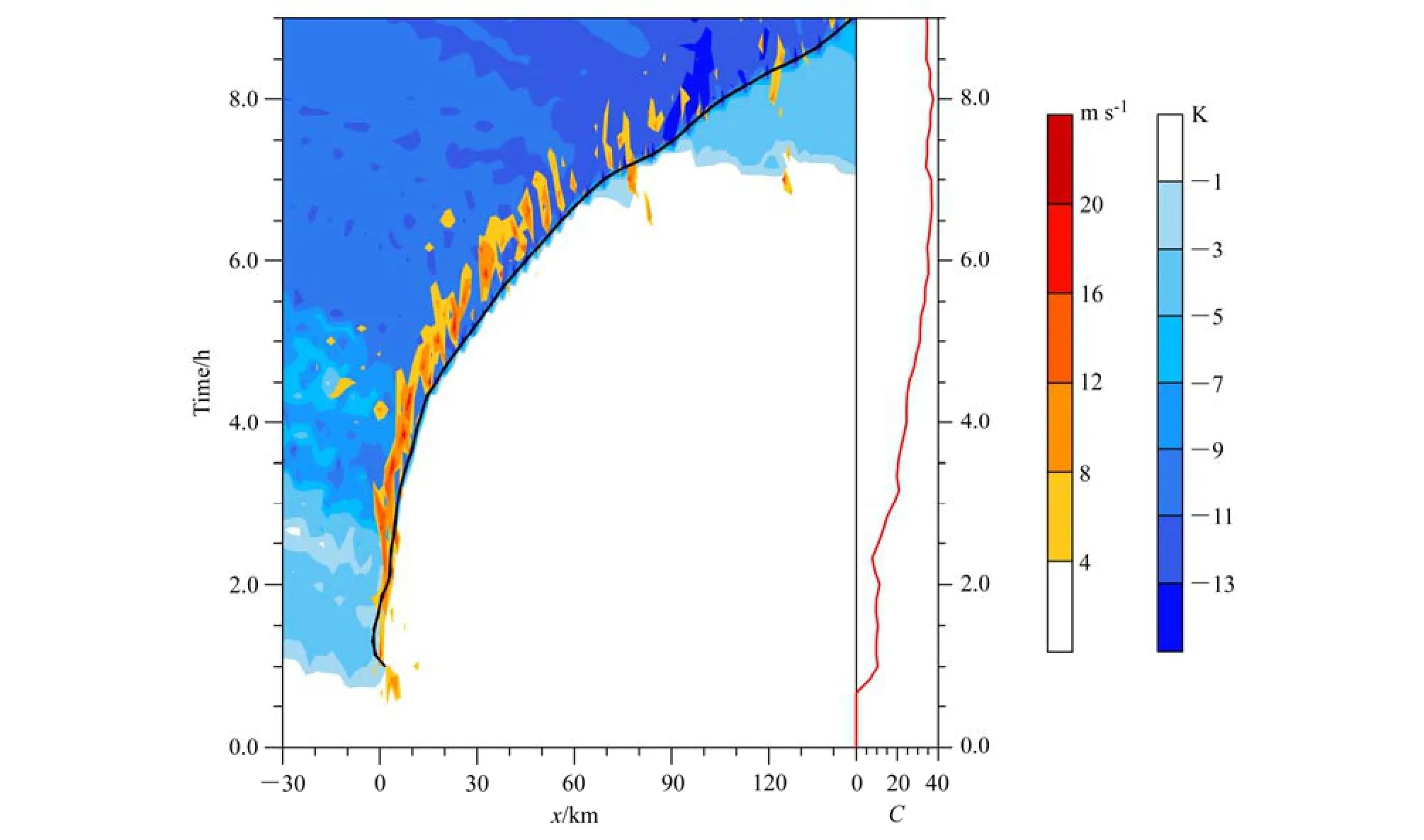
图3 对照试验z=5 km高度上垂直速度、地面扰动位温的时空分布以及冷池强度随时间变化。左图中，暖色阴影表示垂直速度（只给出速度大于4 m s−1的值），冷色阴影为地面扰动位温分布（只给出小于−1 K的值），黑色实线表示冷池前沿线位置。右图中，红色实线表示冷池强度随时间变化Fig. 3 Depiction of the control simulation: (left) temporal–spatial diagram for vertical velocity (warm colors; values less than −4 m s−1not plotted) at 5 km and the surface perturbation potential temperature (cold colors; values greater than −1 K not plotted), in which the black solid line represents the leading edge of the surface cold pool; (right) the strength of the cold pool

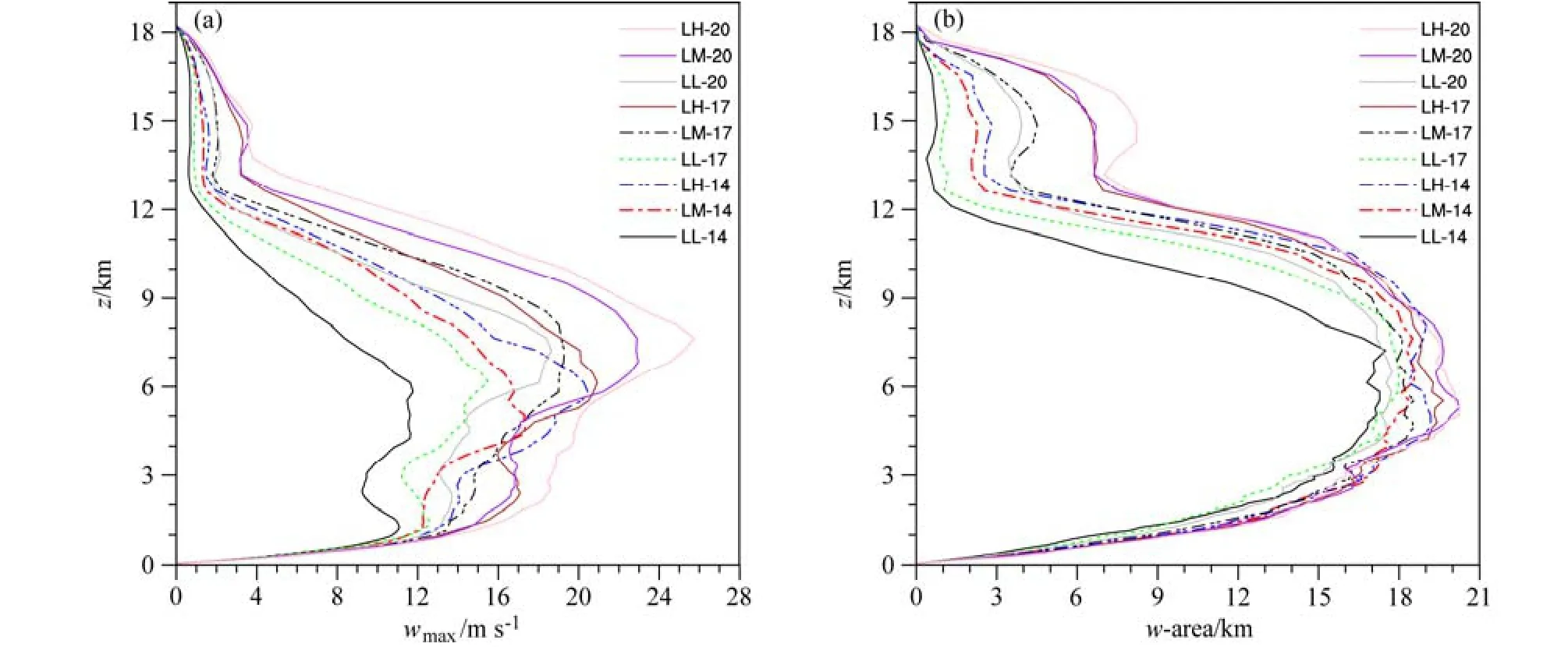
图4 低层切变条件下各试验的（a）最大垂直速度（wmax）的时间（3～7 h）平均以及（b）3～7 h时间内大于1 m s−1的垂直速度所覆盖区域（w-area）的平均值随高度的分布Fig. 4 Temporally averaged (3–7 h) vertical profiles of the (a) maximum updraft speed (wmax) and (b) fractional area of the updraft speed (w-area) more than 1 m s−1

飑线强度用最大垂直速度以及超过1 m s−1的垂直速度所覆盖区域来表示（Takemi, 2014）。图4给出了最大垂直速度和垂直上升运动所覆盖区域在3～7 h内时间平均（时间t包含了对照试验的前3小时积分时间）的垂直分布。总的来看，最大垂直速度在1 km高度以上开始显著增大，而在9 km以上则明显减小，峰值集中在5～8 km。在混合层比湿相同的情况下，Us值愈大则峰值愈大，如LM-20试验的峰值明显大于 LM-17试验，LM-17试验又明显大于LM-14试验。说明增大低层环境垂直风切变有利于飑线强度增强，反之亦然。各试验的垂直上升运动所覆盖区域在中低层无明显差异，高层却明显不同。值得注意的是，各试验高层垂直上升运动覆盖区域的大小顺序与其中层最大垂直速度的大小顺序相同，即用这两种方式表示飑线的强度具有一致性。

为了反应飑线强度的变化趋势，计算了各小时内最大垂直速度均值及其标准偏差（图5）。同样在水汽适中的条件下，增大低层环境垂直风切变（LM-20）所对应的各时间段的均值较对照试验或减小低层环境垂直风切变（LM-14）更大，这与上述的结论是一致的。另外，从均值随时间的变化来看，LM-17试验与LM-20试验的均值先增强后减弱，而LM-14试验则单调递减。即减小低层环境垂直风切变会明显减弱飑线的强度。

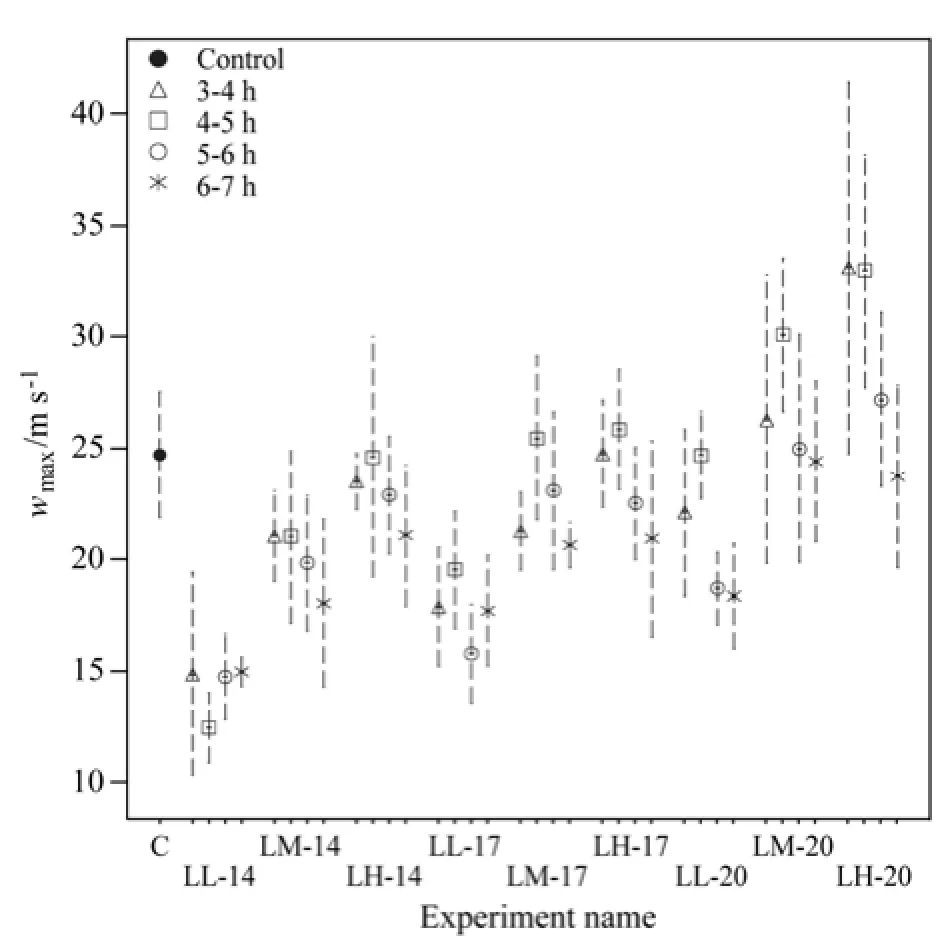
图5 低层切变条件下不同试验各小时内最大垂直速度均值（不同记号表示不同时间段内的均值）及其标准偏差（虚线）。横坐标为各个试验名称（C表示对照试验），纵坐标则为最大垂直速度均值大小（单位：m s−1）Fig. 5 The means (symbols) and standard deviations (dashed lines) of the maximum updraft speed during integrating 2–3 h (filled circle), 3–4 h (asterisks), 4–5 h (circles), 5–6 h (squares), and 6–7 h (triangles) for all experiments. The x-axis is the name of experiments (the character C represents the control experiment). The vertical axis is the mean of maximum vertical

3.2 飑线强度对环境垂直风切变的响应分析

图6、图7分别为减小（LM-14）和增加（LM-20）低层环境垂直风切变试验不同发展时刻的扰动位温、扰动比湿、风场的垂直剖面图。减小低层切变后，无论是对流高度还是扰动比湿大小（负值区，可大致反应降水强度）相较对照试验（图 2）都明显减弱，这与3.1节中结论一致。从移动速度来看，t=1 h时对照试验的冷池前沿位于x=12 km附近，而LM-14试验已达到x=18 km处，即环境垂直风切变的减小使得飑线移动速度加快。从图8a中LM-14，LM-17，LM-20三个试验的低层平均水平速度（水平方向上为冷池前沿线至其后侧20 km，垂直方向为0～1 km共10层的水平速度平均）也可以看出，环境垂直风切变愈大，平均水平风速愈小。Wakimoto（1982）以及Mueller and Carbon（1987）的观测分析表明对于大多数对流风暴来说其传播速度由风暴产生的冷池的移动速度决定，因为新的风暴单体极易被冷池前沿的阵风锋触发从而维持整个风暴系统例如飑线的发展维持。在图 6a中上升运动存在两个中心，一个位于冷池前沿（x=18 km），一个位于x=12 km处。即在开始阶段，飑线移速的加快使得冷池前沿阵风锋触发的对流与中层凝结潜热释放激发的上升运动出现分离，t=5.0 h时这种分离不再明显，而随着飑线的发展，这一分离再次显现（图6c、6d），且在t=6.5 h时出现明显分离。增加低层切变后（图7），飑线移速减小，上升运动并没有出现如对照试验所出现的不连续现象，且无论是从扰动比湿（负值区）还是对流高度来看，都较对照试验明显增强。依据第二部分中冷池的计算公式，给出了这三组试验的冷切比随时间的变化曲线（图 8b），可以发现低层切变越小，冷切比越大，即在切变发生改变的情况下，RKW理论定量的解释了飑线强度变化的原因。而通过分析环流结构的变化，则具体的展现了飑线强度变化的内部机理。

以上分析表明，飑线前侧湿空气被抬升至中高层，形成飑线系统的上升气流，湿空气抬升凝结释放潜热使得气流进一步上升，湿空气凝结形成雨滴降至地面，降水同时拖拽空气下沉；雨水的蒸发使得近地面温度降低，形成中尺度高压区域。这两者共同作用下在冷池区域形成辐散气流，向x正方向的辐散气流（阵风锋）与入流形成辐合从而触发新的对流产生，并使得飑线向前推进。低层环境垂直风切变的减小使得辐合中心向右侧推进速度加快，从而使得冷池前沿阵风锋触发的新的对流与中层凝结潜热释放激发的上升运动分离，飑线强度减弱，反之亦然。

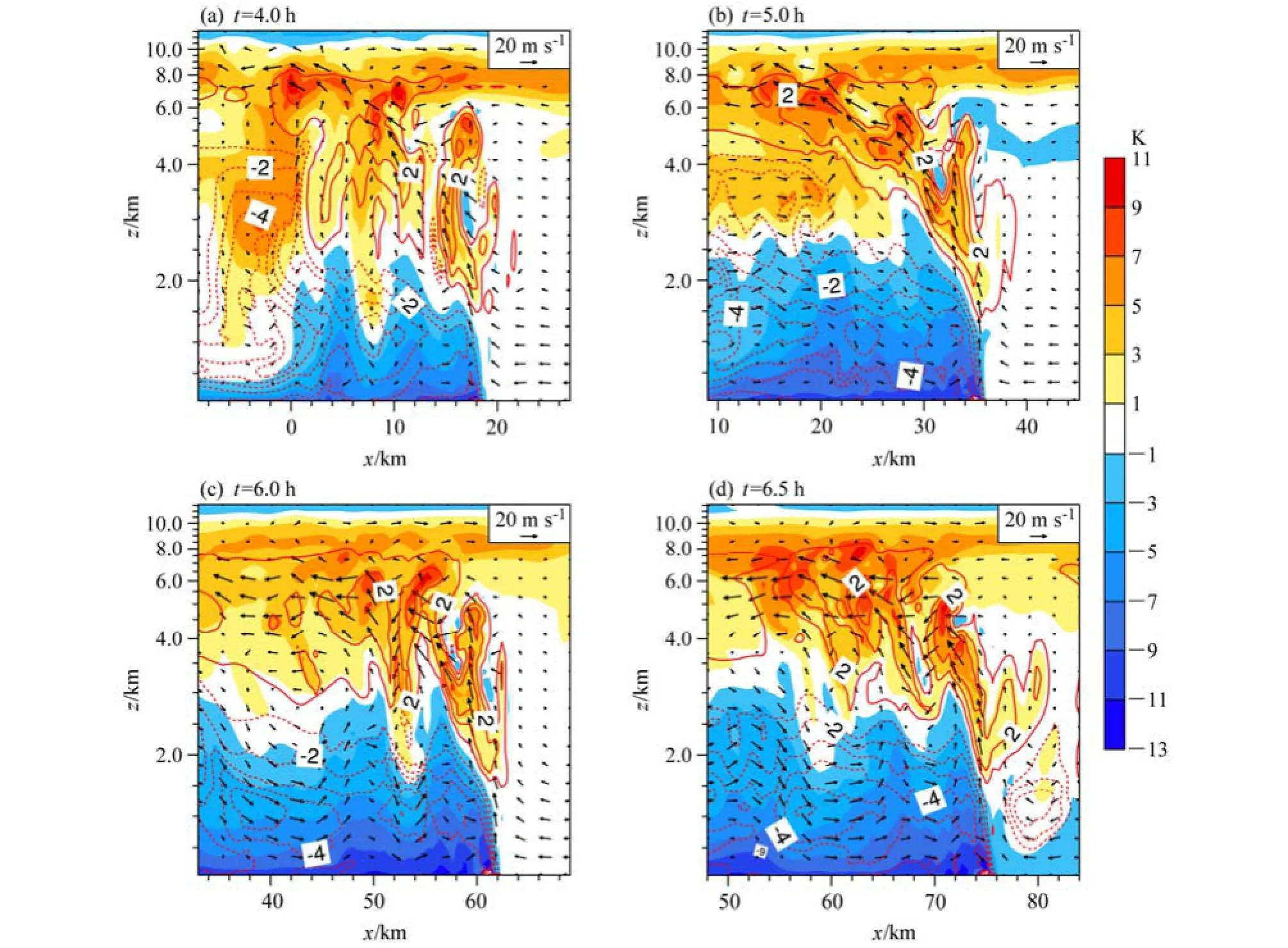
图6 同图2，但为LM-14试验Fig. 6 As in Fig. 2, but for experiment LM-14

4 低层水汽变化对飑线强度的影响

Meng et al.（2013）通过统计中国东部的飑线发现，在同样的不稳定条件下不同程度的比湿影响着飑线的发生程度，即比湿的大小会影响飑线的发生发展。因此本章将低层比湿作为敏感性因子，探讨在比湿改变的条件下飑线强度如何变化，并从飑线系统的内部环流结构出发解释这一强度变化原因。

与垂直风切变的敏感性试验类似，在这组敏感性试验中将敏感性因子改为低层比湿，而垂直风切变则与对照试验一致。试验设计了三种不同的混合层比湿：12 g kg−1、14 g kg−1、16 g kg−1，代表低层的水汽含量较低（L）、适中（M）、及较高（H）。不同的混合层比湿对应的环境CAPE也不相同，分别为1144 J kg−1、2219 J kg−1、3500 J kg−1。就飑线的发展演变来看，CAPE的变化范围很大，一般而言，CAPE在1000 J kg−1左右时，对形成一般的飑线系统比较有利，而当其超过2200 J kg−1时，则有可能形成较强的飑线系统（Bluestein et al., 1987；Parker and Johnson, 2000；Weckwerth, 2000）。各试验命名见表1。

4.1 飑线强度对低层水汽的响应

图4也可反应飑线强度对低层水汽的响应。从图中可以看出，在Us相同的情况下，低层比湿愈大则峰值愈大，如LH-17试验的峰值明显大于LM-17试验，而LM-17试验又明显大于LL-17试验。图4b所呈现的图像反应出了同样的结果。从飑线强度的变化趋势图（图 5）也同样可以看出，随着低层比湿的增加，各时间段的均值会随之增大。因此以得出这样的结论：低层水汽供应越充分，越有利于飑线强度的增强。孙建华等（2014）对实际个例的水汽敏感性试验也印证了这一结论。

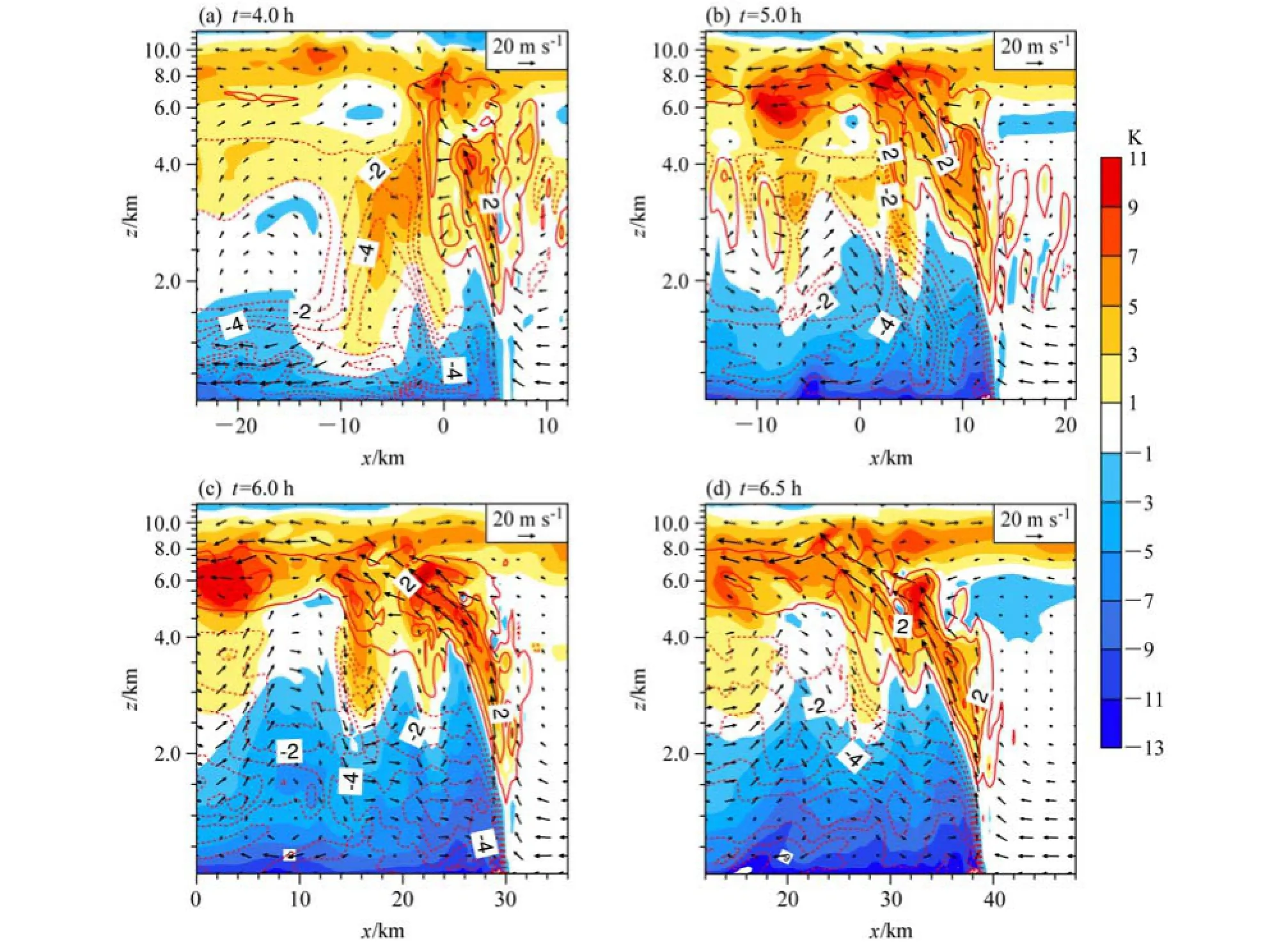
图7 同图2，但为LM-20试验Fig. 7 As in Fig. 2, but for experiment LM-20

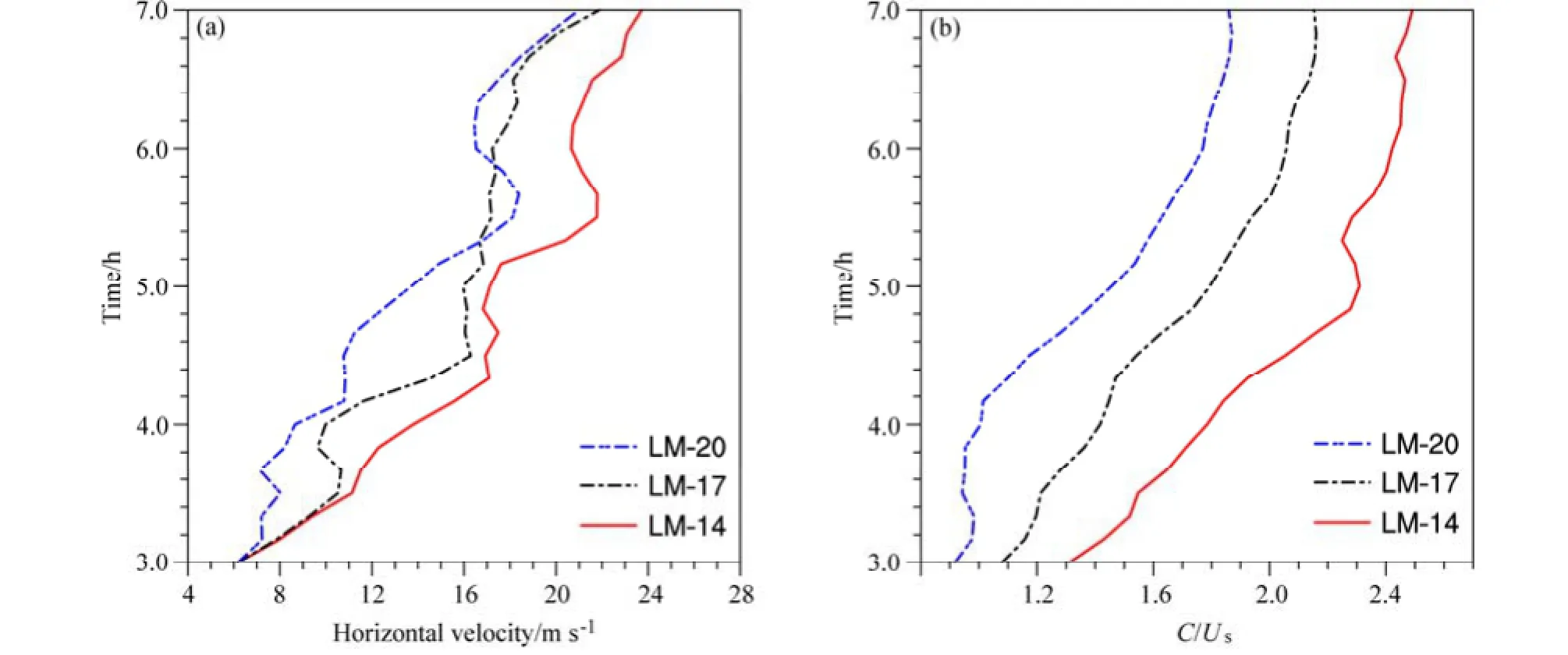
图8 LM-14（红线）、LM-17（黑线）、LM-20（蓝线）三个试验（a）平均水平速度和（b）冷池强度与低层环境垂直风切变的比值（C/Us）随时间变化Fig. 8 Time series of (a) average horizontal velocity and (b) the ratio between the strength of cold pool and low-level VWS (C/Us) for experiments LM-14 (red line), LM-17 (black line), and LM-20 (blue line)

4.2 飑线强度对低层水汽的响应分析

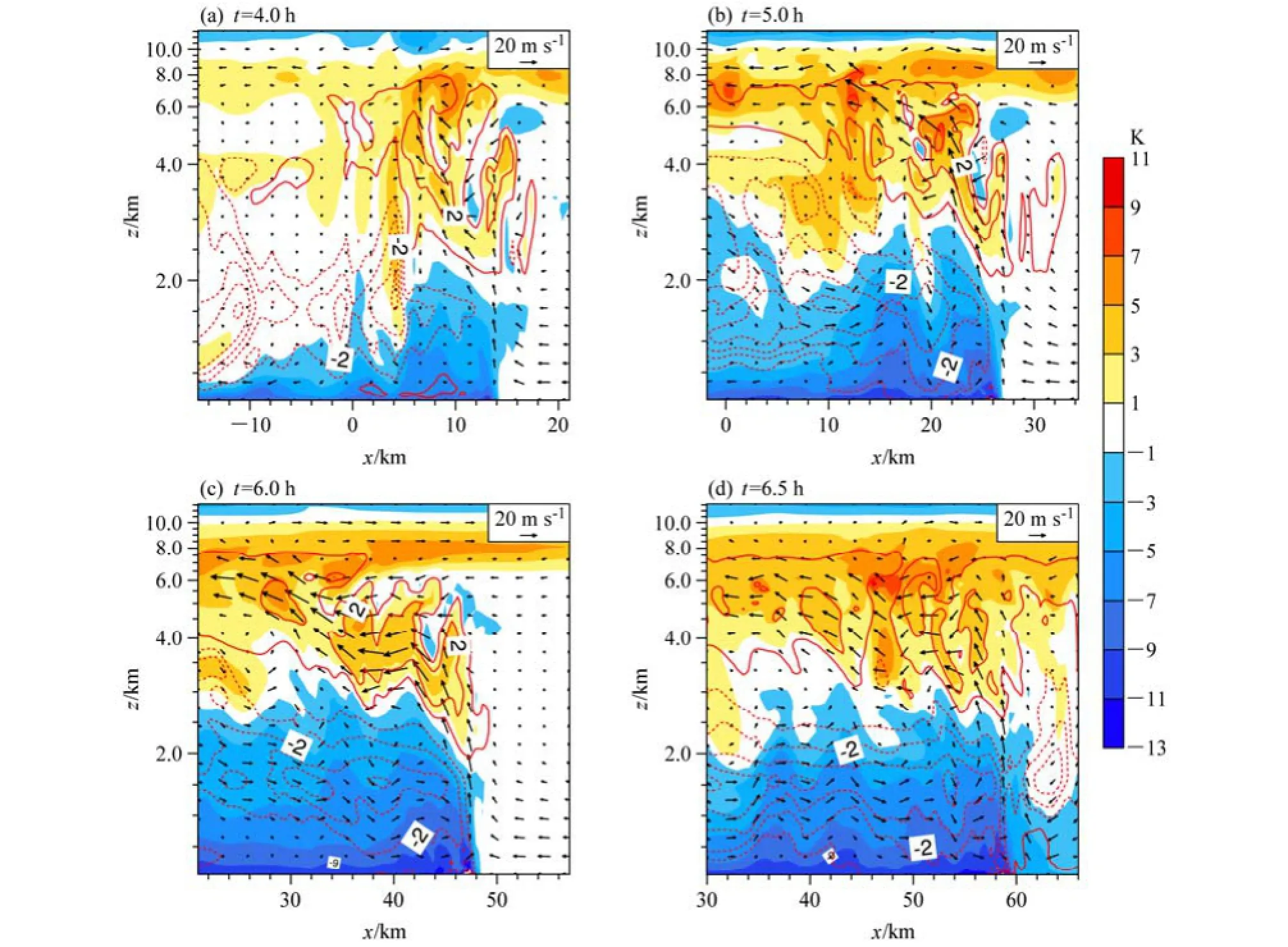
图9 同图2，但为LL-17试验Fig. 9 As in Fig. 2, but for experiment LL-17

图9、图10分别为减少（LL-17）和增加（LH-17）低层比湿试验不同发展时刻的扰动位温、扰动比湿、风场的垂直剖面图。与对照试验（图2）相比较可以发现，三者在飑线推进速度上存在差异，但并不明显，即改变低层比湿后，飑线强度变化的原因与改变环境垂直风切变的有所不同。而在垂直上升运动、扰动位温强度（尤其是正值），扰动比湿强度上，三者差异明显。LL-17试验最弱，LH-17最强，LM-17居中。即低层比湿愈大，飑线强度愈强，这与4.1的结论一致。从扰动比湿（正值）来看，LH-17试验较LL-17试验扰动幅度更大，即在低层增加比湿的条件下，输送到中层的水汽更多，相应的凝结潜热释放也更多（从扰动位温正值可看出）；比湿的增加使得飑线降水强度也相应增加，这从冷池前沿线后方的扰动比湿负值大小可以看出。降水愈强，说明空气中的水汽凝结成液态水愈多，比湿变化也就越大。减小低层比湿的情况下（图9），中层释放的凝结潜热相对较少，从而使得飑线发展后期中层不再出现明显的上升运动或上升运动较弱（图9c、9d），而增加低层比湿则与此相反；低层比湿的减小使得冷池前沿阵风锋触发的对流强度减小，这与CAPE的释放大小有关。

为了反映各试验在飑线移至时环境CAPE的释放大小，我们对x=0 km至x=30 km范围内的CAPE进行了区域平均，并给出了其随时间的变化曲线（图11）。从图中可以看出，所有试验的平均CAPE随时间基本呈现出单调递减的趋势，并最终都趋近于零，这是飑线过境后，环境CAPE释放的结果。而在不同的条件下，平均CAPE的初始值及变化曲线存在显著差异，在低层切变相同的情况下，低层比湿越大，则平均CAPE的变化幅度越大，即CAPE释放值越大。对比图中LH-17与LL-17试验的变化曲线可以发现，前者较后者所释放的CAPE更大，这决定了各自在冷池前沿新激发的对流强度LL-17试验要显著弱于LH-17试验。从图中还可以看出，低层比湿相同的情况下，切变越大，则平均CAPE从初始值递减至零所需时间越长，即飑线移动的速度越慢。而在低层切变一致时，无论低层比湿条件如何，递减至零所需时间基本相同。即飑线的移动速度主要与低层切变有关，低层比湿则影响不大。

以上分析表明，在保持低层环境垂直风切变不变的情况下，改变低层比湿条件，飑线的移动速度未发生明显变化，而输送至飑线系统中高层的水汽却存在不同，这使得水汽凝结释放潜热量不同，进而使得中高层的垂直上升运动强度出现差异；此外，低层比湿的改变也使得环境CAPE发生变化，从而影响新激发的对流强度。即减小（增加）低层比湿一方面会使得冷池前沿的阵风锋触发的新的对流强度减弱（增强），另一方面输送到中层的水汽减少（增加），相应的凝结潜热释放减小（增大），进而使得中层的上升运动减弱（增强），两处上升运动的减小及分离（增强并相互贯通）使得飑线强度减弱（增强）。

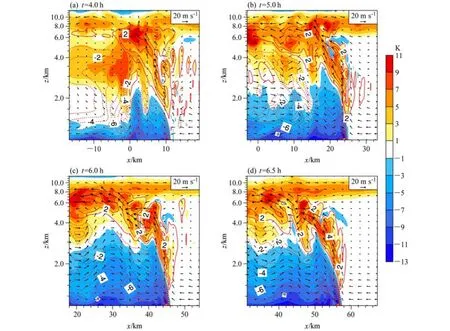
图10 同图2，但为LH-17试验Fig. 10 As in Fig. 2, but for experiment LH-20

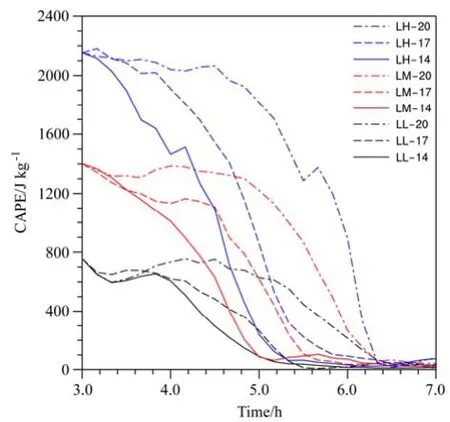
图11 各试验区域平均（x=0～30 km）的对流有效位能（CAPE）值随时间变化Fig. 11 Time series of regional average (x = 0–30 km) convective available potential energy (CAPE) for all experiments

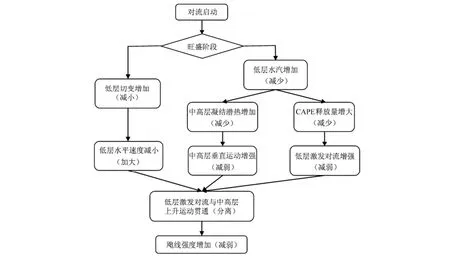
图12 环境参数影响下飑线内部结构调整及其对飑线强度影响的示意图Fig. 12 Schematic diagram of squall line internal restructuring and variation in intensity for the effects of environmental parameters

5 结论与讨论

本文利用ARPS模式对飑线发生发展过程进行了二维理想数值试验，并从飑线系统内部动量、热量、水汽等物理因子配置的变化过程入手，分析了飑线系统组织化对流的形成、发展和消亡机制，讨论了当低层环境垂直风切变和水汽等环境要素场发生变化时，系统内部各物理因子的响应过程及其对飑线系统强度变化的影响。

研究表明，在深对流演变过程中，飑线系统内部出现动量、热量以及水汽的区域性再分配，导致系统内环流结构、冷池强度发生改变，并依此对飑线的组织化程度产生影响。通过飑线强度对低层环境垂直风切变和水汽的敏感性试验发现，环境因素的变化同样会使飑线系统内部出现动量、热量、水汽的再分配过程，并依此对飑线强度产生影响。改变低层环境垂直风切变时，飑线系统内部动量、热量以及水汽的再分配使得飑线移速发生变化，从而影响飑线强度：当增大（减小）低层环境垂直风切变时，飑线后侧低层的水平速度减小（增加），从而使得飑线移速减慢（加快），新激发的对流与中高层的垂直运动相互贯通（分离），飑线强度得以增强（减弱）；改变低层水汽时，飑线系统内部动量、热量以及水汽的再分配则主要影响中高层的垂直运动以及新触发的对流，从而使得飑线强度发生变化：增加（减少）低层水汽时，输送到中高层的水汽增加（减少），水汽凝结释放潜热得以增加（减少），这使得中高层的垂直运动增强（减弱）；同时，增加（减少）低层水汽使得飑线移至时环境所释放的 CAPE增大（减小），冷池前沿所激发的对流增强（减弱）。两者作用下新激发的对流与中高层的垂直运动得以相互贯通（分离），飑线强度增强（减弱）。飑线强度对低层切变及水汽的响应可由示意图图12来表示。

本文对飑线发展过程中其强度对低层环境垂直风切变和水汽的响应及其原因进行了详细的研究，但文章涉及的数值试验皆为两维结构，这与实际飑线的三维结构存在差异，因此后续的研究所有试验将扩展到三维。此外，理想试验只代表理想环境配置条件下飑线的发展变化过程，下一步，将利用实际飑线个例的观测和数值模拟结果进行诊断分析。

参考文献（References）

Bluestein H B, Jain M H. 1985. Formation of mesoscale lines of precipitation: Severe squall lines in Oklahoma during the spring [J]. J. Atmos. Sci., 42 (16): 1711–1732.

Bluestein H B, Marx G T, Jain M H. 1987. Formation of mesoscale lines of precipitation: Non-Severe squall lines in Oklahoma during the spring [J]. Mon. Wea. Rev., 115 (11): 2719–2727.

陈明轩, 王迎春. 2012. 低层垂直风切变和冷池相互作用影响华北地区一次飑线过程发展维持的数值模拟 [J]. 气象学报, 70 (3): 371–386. Chen Mingxuan, Wang Yingchun. 2012. Numerical simulation study of interactional effects of the low-level vertical wind shear with the cold pool on a squall line evolution in North China [J]. Acta Meteorologica Sinica (in Chinese), 70 (3): 371–386.

Coniglio M C, Corfidi S F, Kain J S. 2012. Views on applying RKW theory: An illustration using the 8 May 2009 derecho-producing convective system [J]. Mon. Wea. Rev., 140 (3): 1023–1043.

Fovell R G, Ogura Y. 1988. Numerical simulation of a mid-latitude squall line in two dimensions [J]. J. Atmos. Sci., 45 (24): 3846–3879.

Fujita T. 1955. Results of detailed synoptic studies of squall lines [J]. Tellus, 7 (4): 405–436.

Houze Jr R A, Biggerstaff M I, Rutledge S A, et al. 1989. Interpretation of Doppler weather radar displays of midlatitude mesoscale convective systems [J]. Bull. Amer. Meteor. Soc., 70 (6): 608–619.

Lin Y L, Farley R D, Orville H D. 1983. Bulk parameterization of the snow field in a cloud model [J]. J. Climate Appl. Meteor., 22 (6): 1065–1092.

Meng Z Y, Yan D C, Zhang Y J. 2013. General features of squall lines in East China [J]. Mon. Wea. Rev., 141 (5): 1629–1647.

Mueller C K, Carbone R E. 1987. Dynamics of a thunderstorm outflow [J].J Atmos. Sci., 44 (15): 1879–1898.

Newton C W. 1950. Structure and mechanism of the prefrontal squall line [J]. J. Meteor., 7 (3): 210–222.

Parker D J. 1998. The dependence of cold-pool depth on source conditions [J]. Mon. Wea. Rev., 126 (2): 516–520.

Parker M D. 2008. Response of simulated squall lines to low-level cooling [J]. J. Atmos. Sci., 65 (4): 1323–1341.

Parker M D, Johnson R H. 2000. Organizational modes of midlatitude mesoscale convective systems [J]. Mon. Wea. Rev., 128 (10): 3413–3436.

Parker M D, Johnson R H. 2004. Structures and dynamics of quasi-2D mesoscale convective systems [J]. J. Atmos. Sci., 61 (5): 545–567.

Rotunno R, Klemp J B, Weisman M L. 1988. A theory for strong, long-lived squall lines [J]. J. Atmos. Sci., 45 (3): 463–485.

孙建华, 郑淋淋, 赵思雄. 2014. 水汽含量对飑线组织结构和强度影响的数值试验 [J]. 大气科学, 38 (4): 742–755. Sun Jianhua, Zheng Linlin, Zhao Sixiong. 2014. Impact of moisture on the organizational mode and intensity of squall lines determined through numerical experiments [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 38 (4): 742−755.

Takemi T. 2006. Impacts of moisture profile on the evolution and organization of midlatitude squall lines under various shear conditions [J]. Atmospheric Research, 82 (1–2): 37–54.

Takemi T. 2007. A sensitivity of squall-line intensity to environmental static stability under various shear and moisture conditions [J]. Atmospheric Research, 84 (4): 374–389.

Takemi T. 2014. Convection and precipitation under various stability and shear conditions: Squall lines in tropical versus midlatitude environment [J]. Atmospheric Research, 142: 111–123.

Thorpe A J, Miller M J, Moncrieff M W. 1982. Two-dimensional convection in non-constant shear: A model of mid-latitude squall lines [J]. Quart. J. Roy. Meteor. Soc., 108 (458): 739–762.

Wakimoto R M. 1982. The life cycle of thunderstorm gust fronts as viewed with Doppler radar and rawinsonde data [J]. Mon. Wea. Rev., 110 (8): 1060–1082.

Weckwerth T M. 2000. The effect of small-scale moisture variability on thunderstorm initiation [J]. Mon. Wea. Rev., 128 (12): 4017–4030.

Weisman M L, Klemp J B. 1982. The dependence of numerically simulated convective storms on vertical wind shear and buoyancy [J]. Mon. Wea. Rev., 110 (6): 504–520.

Weisman M L, Rotunno R. 2004. “A theory for strong long-lived squall lines” revisited [J]. J. Atmos. Sci., 61 (4): 361–382.

Wyss J, Emanuel K A. 1988. The pre-storm environment of midlatitude prefrontal squall lines [J]. Mon. Wea. Rev., 116 (3): 790–794.

Xue M, Droegemeier K K, Wong V. 2000. The Advanced Regional Prediction System (ARPS)—A multi-scale nonhydrostatic atmospheric simulation and prediction model. Part I: Model dynamics and verification [J]. Meteor. Atmos. Phys., 75 (3–4): 161–193.

资助项目 国家重点基础研究发展计划（973计划）项目2013CB430103，国家自然科学基金项目41275002、41230421，江苏省高校自然科学研究重大项目14KJA170005，江苏省“333高层次人才培养工程”项目，灾害天气国家重点实验室开放课题（2014LASW-B08）

Funded by National Key Basic Research and Development Project of China (973 Program) (Grant 2013CB430103), National Natural Science Foundation of China (Grants 41275002 and 41230421), The Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant 14KJA170005), “333 High-Level Talent Development Program” in Jiangsu Province, National Key Laboratory of Disaster Weather (Grant 2014LASW-B08)

文章编号1006-9895(2016)04-0689-14 中图分类号 P446

文献标识码A

doi:10.3878/j.issn.1006-9895.1505.14337

收稿日期2014-12-12；网络预出版日期 2015-07-07

作者简介张建军，男，1989年出生，硕士研究生，主要从事中尺度研究。E-mail: zhangjj_nuist@126.com

通讯作者钟玮，E-mail: wzhong_vivian@126.com

Impact of Vertical Wind Shear and Moisture on the Organization of Squall Lines

ZHANG Jianjun1, 2, WANG Yongqing2, and ZHONG Wei3, 4
1 Hunan Climate Center, Changsha 410118
2 Pacific Typhoon Research Center, School of Atmospheric Sciences, Nanjing University of Information Science ＆amp; Technology, Nanjing 210044
3 Institute of Meteorology and Ocean, PLA University of Science and Technology, Nanjing 211101
4 Key Laboratory of Mesoscale Severe Weather (Nanjing University), Ministry of Education, Nanjing 210093

AbstractThe redistribution of physical factors and its impacts on the intensity of squall lines under the influence oflow-level Vertical Wind Shear (VWS) and moisture content are examined through two-dimensional idealized simulations with the ARPS model (the University of Oklahoma’s Advanced Research Prediction System). It shows that the redistribution of momentum, heat and moisture during the evolution of squall lines leads to the change of inner vertical circulation and the configuration of perturbation temperature and humidity, which affects the organization of deep convection and the intensity of the system. The results of sensitivity tests of low-level VWS and moisture content show that increasing (decreasing) the low-level VWS decelerates (accelerates) the propagation of the squall line, and makes the connection (separation) between the mid-level upward current and the new forced updrafts at the front edge of the cold pool, which corresponds to the intensification (weakening) of the squall line. On the other hand, increasing (decreasing) the low-level moisture content results in an increase (decrease) of moisture delivery from the low to middle level, which enhances (weakens) the mid-level latent heating and upward movement. Energy analysis indicates that the low-level moisture change influences the release of Convective Available Potential Energy (CAPE), and the intensity of the new convection. The combined effects of latent heating and CAPE released from low-level moisture change also affect the squall line intensity through exerting an influence on the organization of the upper-level upward currents and the new forced updrafts at the front edge of the cold pool.

KeywordsSquall line, Numerical simulation, Cold pool, Vertical Wind Shear, Moisture