线性平散时变系统可靠镇定

甘乃峰　谷晓沛鞍山师范学院　（鞍山114007）



线性平散时变系统可靠镇定

甘乃峰谷晓沛
鞍山师范学院（鞍山114007）

摘要研究了套代数框架下线性离散时变系统镇定控制器的分解，它是从另一个角度研究可靠镇定问题，并给出了两个控制器同时镇定系统以及一个镇定控制器分解成两个镇定控制器的结果，上述结果中控制器的设计依赖于唯一参数的选取。

关键词套代数；线性离散时变系统；控制器分解中图分类号：O1-0

文献标识码：A

文章编号：1003-3319（2016）01-00032-02

控制系统的可靠镇定考虑的是设计多个控制器同时镇定系统，当其中部分控制器失效时，剩余控制器仍旧控制系统，它是多重系统同时镇定的对偶问题.文［1，2］首先提出可靠镇定问题，并从数学框架角度出发用较少的控制器实现系统的可靠镇定。

本文主要研究了在套代数框架下平散时变系统的可靠镇定问题，即给定平散时变系统和一个镇定控制器情况，设计另一个控制器，使得它们一起镇定系统，以及一个镇定控制器分解方法。

1　套代数相关理论

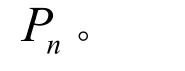
定义2.1［3］：如果N是一个完备套，是它的对应的投影族，

是一个与P对应的套代数。其中B（H）是H中所有有界线性算子构成的代数。再令，那么也是空间上的一个完备套，与其对应的套代数为

值得注意的是，在标准正交基下，套代数中的元素的矩阵表示是一个下三角型矩阵。

关联性是具有现实意义，即未来的输入不可能对现时的输出结果产生影响。

定义2.3［3］：He空间上，按预解拓扑连续的关联线性变换称为线性系统。

将He上所有线性系统构成的集合记为L（H）。

2　控制器的设计与分解

引理3.1［3］如果B（H）f∈和，那么f是可逆的。

下面给出文［3］中介绍的反馈系统是镇定的充要条件的对偶形式。

推论3.2［3］如果系统L（H）L∈具有左互素分解和控制器K具有右互素分解，则是稳定的充要条件在S中可逆。

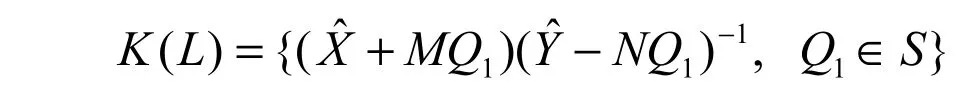
设

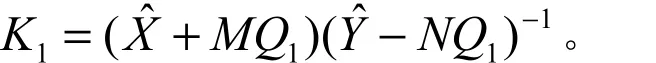
已知镇定系统L，则

由双Bezout恒等式可得

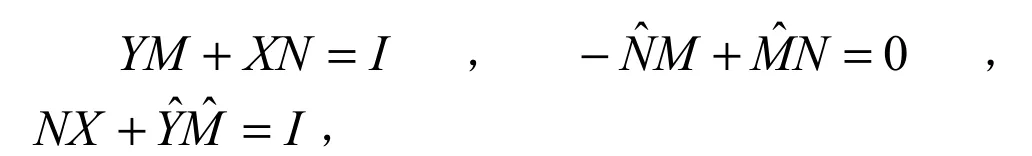
带入上式整理得

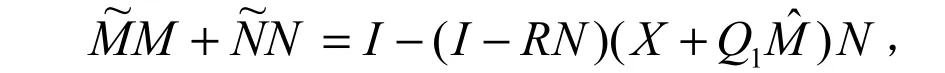
因此，

选择Q1使得，只要，就有

由引理3.1得MM+NN 在S中可逆，由推论3.2得K2镇定系统L。由此可知，当K1镇定系统L时，则存在控制器K2也镇定系统L，并且K1+ K2镇定系统L。证毕

控制器的分解是从另外的一个角度考虑可靠镇定问题，即给定镇定对象L∈L（H）和控制器K，如何分解K=K1+ K2，使得K1及K2单独作用时均能有效地镇定系统L。

定理3.4：镇定系统L∈L（H）的控制器K=（Y-QNˆ）-1（X+QMˆ），Q∈S在满足条件

（I +MY-MQNˆ）-1∈S 的条件下可分解为

K=K1+ K2且K1，K2分别镇定系统L。

证明：设可镇定系统L的左右互素分解分别为L =Mˆ-1Nˆ=NM-1，其中M，N，Mˆ，Nˆ∈S。则镇定系统L的所有控制器为：

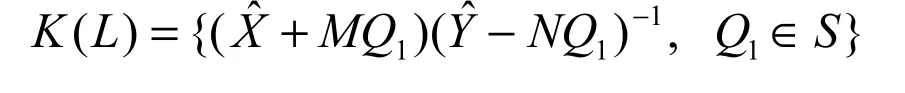
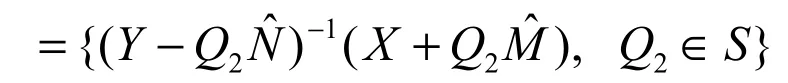
参数稍作变化，不妨设

其中A，B∈S，待定。考虑

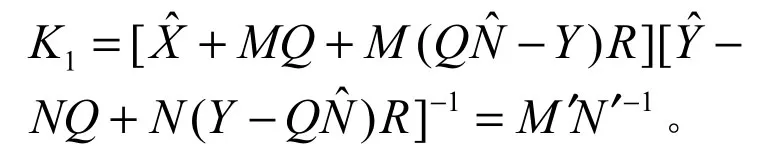
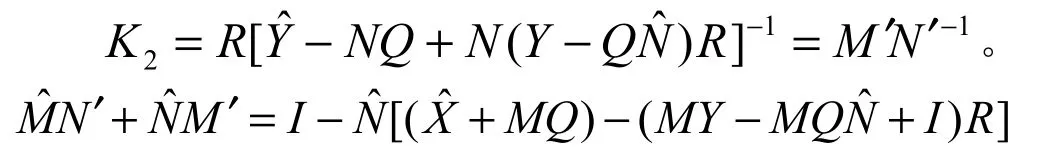
参考文献

［1］D. D. Siljak. On reliability of control［C］. In Proc. 17th IEEE Conf. Decision Control，1978，687-694.

［2］D. D. Siljak. Reliable control using multiple control systems［J］. Int. J. Contol，1980，31（2）：303-309.

［3］Vidyasagar M and N Viswanadham. Reliable stabilization using a multi-controller configuration. Automatica. 1985，21（5）：599-602.

［4］陈祥杰，王诗宓，方崇智.控制系统的可靠镇定［C］.中国控制会议论文集，太原，1985，90-95.

［5］T.Q.Yu，The transitivity in simultaneous stabilization［J］. Systems Control Letters. 2011，60（1）：1-6.

（责任编辑：文婷）