基于边坡单元的水库库岸稳定性层次分析与评价
许 波, 谢谟文, 何兴东, 胡 嫚
(1.北京科技大学 土木与环境工程学院, 北京 100083; 2.中国电建集团昆明勘察设计研究院有限公司, 云南 昆明 650051; 3.西南大学 工程技术学院, 重庆 400715)
基于边坡单元的水库库岸稳定性层次分析与评价
许 波1, 谢谟文1, 何兴东2, 胡 嫚3
(1.北京科技大学 土木与环境工程学院, 北京 100083; 2.中国电建集团昆明勘察设计研究院有限公司, 云南 昆明 650051; 3.西南大学 工程技术学院, 重庆 400715)
摘要:[目的] 分析影响孟底沟水库库岸稳定的影响因素,为水库库岸稳定性评价提供新思路。[方法] 在工程地质条件分析及不良地质现象解译的基础上,运用边坡单元将各岸坡段划分为独立的研究对象,分析影响库岸稳定的诸多因素,把边坡单元的三维安全系数作为稳定性评价的基本指标,对影响边坡稳定的各因素采用层次分析法,建立基于边坡单元的库岸稳定性分段层次分析与评价方法。[结果] 将该方法运用在工程实例中,结果表明其具有一定的可靠性和实用性。[结论] 以边坡单元为研究对象,运用层次分析法可以有效地分析水库库岸的稳定性,为工程决策提供支持。
关键词:库岸稳定; 遥感解译; 边坡单元; 层次分析法; 三维分析
文献参数: 许波, 谢谟文,何兴东.基于边坡单元的水库库岸稳定性层次分析与评价[J].水土保持通报,2016,36(3):290-296.DOI:10.13961/j.cnki.stbctb.2016.03.050
水库蓄水过程及运行阶段,改变河谷岸坡的自然平衡条件后,库岸岩土体的稳定性称为库岸稳定[1]。在此过程中,库岸所处的地质环境将发生显著改变,自然平衡条件遭到破坏,引起岸坡冲刷、剥蚀、坍塌,库岸逐渐后退,直到达到新的平衡状态为止。由于大部分水库都会有库岸不稳定问题[2],国内外很多专家学者都对库岸稳定性做了一些研究。
在库水对岸坡的水岩作用研究方面:Fabio Luino[3]以降水诱发滑坡为对象,从不同角度对水岩(土)体系中地下水在边坡失稳破坏中的作用机制进行了分析研究,对失稳提出了不同的解释;仵彦卿[4]总结了地下水对岩土体产生物理、化学以及力学的作用;马水山[5]等从水岩作用的材料力学效应、水力学效应、化学效应和地震效应4个方面进行了分析;王思敬等[6]论述了水库地区水环境系统的变化及水岩作用类型和机制,在此基础上讨论了库区地质环境的变化和环境灾害的发生,提出了以水环境变化和水岩作用为中心的水库地质环境评价和灾害预测研究方向。在库水作用下岸坡稳定性的分析方法研究方面:Morgenstem在不考虑孔压消散的假定基础上,利用极限平衡法探讨了库水位变化对均质岸坡安全系数的影响;梁燕、李同录、李萍、陶福平等通过黄金分割方法优化计算分析了库水位下降时岸坡内孔隙水压力的变化及由此引起的岸坡稳定性变化;刘新喜等[7],朱冬林等[8],Lane等[9],利用强度折减法分析了水位变化对边坡安全系数的影响。
在这些分析方法中,每一种方法所考虑的因素都是有限且固定的,而现场的地质环境是复杂多变的,所以,这些方法在实际工程中的应用还需要进一步的完善。而层次分析法AHP[10]根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。所以应用层次分析法对水库区库岸稳定性进行评价是一种比较理想的方法。
本文以孟底沟水电站库区为对象进行库岸稳定研究。该水电站为四川省雅砻江中游第4个梯级水电站,位于甘孜州九龙县与凉山州木里县的交界的雅砻江干流上。研究区域位于青藏高原的东缘沙鲁里山脉与大雪山之间,地处松潘—甘孜造山带南部祝桑弧形构造带以南,位于“川滇巨型菱形断块”内。
本文拟运用边坡单元的理论方法,并采用层次分析法来确定各评价指标的权系数。将边坡单元理论和层次分析法结合在一起,利用层次分析法确定影响边坡单元稳定的各因素的权系数,利用基于GIS研发的3D SlopeGIS模块计算边坡单元的三维安全系数,以其作为库岸稳定性评价的基本指标,并参照边坡单元实际的地形地貌、岩性构造、不良地质现象发育情况等因素予以修正,最终实现对整个库区岸坡稳定性评价。
1研究方法
1.1边坡单元基本理论
大范围研究区域内的滑坡灾害分区方法一般是基于分区单元分析其危险度值或安全系数。分区单元可以是规则的网格单元或复杂的边坡单元。规则网格单元的算法相对简单,但这种均匀分布的网格单元与实际的边坡破坏单元及力学机制、地质、地形及水文没有任何联系。边坡单元定义为一块与邻近区域具有明显不同地形特征的区域[11],而地形的形成本身可以反映地质及水文地质条件的长期作用效果,因此将边坡单元作为分区单元的适用性是极强的,对基于三维力学模型的滑坡灾害分区及常用的多因素统计方法都是适用的。
一个边坡单元实际上是一个曲面,可以用主倾斜方向、主倾斜角、边坡宽度、边坡长度、边坡高度及中心点定义其属性。
从地形的视觉上看,边坡单元可以用特征地形线来进行划分。本文采用谷底线和山脊线来划分边坡单元,即一个汇水区的左右两侧各为一个边坡单元。边坡单元划分的具体方法采用GIS水理分析功能,其步骤如下:
(1) 数字高程DEM栅格数据中凹点检查和处理:对DEM栅格数据数值插值误差引起的标高极低(与周围点相比)的孤立栅格进行标高充填处理。
(2) 水流方向计算:根据相邻栅格的标高比较得到水流方向。
(3) 水流汇集计算:从周围流入到该单元的单元数。
(4) 汇水区,即山脊线的抽出:根据水流方向和水流汇集,即可抽出汇水区。这个汇水区的边界即是要求的山脊线。但由于对一个大范围的研究区域可以有不同规模的汇水区,即要求确定一个阀值来决定汇水区的规模。
为了得到谷底线的分布,我们采用以下的公式(1)对DEM栅格数据进行处理,即可得到一个与原地形反向的地形栅格数据。在此反向的地形栅格数据中,原山脊线的位置变为谷底线,而原谷底线的位置变为山脊线。这样,基于这个反向的地形栅格数据采用同样的水理分析流程,即可得到谷底线的分布。对谷底线和山脊线两个多边形数据集进行联合运算,即可得到边坡单元的数据集。
R-DEM=DEM×(-1)+DEMmax
(1)式中:R-DEM——反向的地形栅格数据; DEM——原地形栅格数据; DEMmax——原地形栅格数据的最大标高值。
边坡单元的大小选定取决于研究对象区域内历史滑坡的平均尺寸,即对于同一区域内具有相同或类似的地形、地质及水文条件的研究对象,可以认为其将来的可能滑坡破坏与过去的滑坡破坏在规模上是一致的。由于在边坡单元的划分过程中,汇水集阀值决定了边坡单元的大小,因此在实际应用时,需要进行多个阀值的对比试算以确定合适的阀值水平。
1.2层次分析法
层次分析法AHP是一种多指标分析评价方法,具有精度高,使用方便的特点。作为一种多因素分析方法,虽然AHP有一定的主观因素在里面,但是基于专家知识,逐一对比每两个影响因子之间的关系,可以有效地将人为误差降至最低。同时在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而采用一致矩阵法,即:① 不把所有因素放在一起比较,而是两两相互比较;② 对比时采用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,以提高准确度。
1.3边坡稳定的控制参数
边坡的稳定性受诸多因素的影响,这些因素包括:地形地貌〔包括坡度坡向、岩体完整度、蓄水位(库水位)等〕、岩性构造(包括岩性、河谷结构、河谷类型、岸坡结构、断层等)和不良地质现象(包括滑坡、崩塌、堆积体、泥石流等)等。对于这些影响因素,通过层次分析法分析其对稳定性的影响程度,结合三维安全系数评价其综合稳定性,建立的边坡单元稳定性综合评估指标如式(2)所示,其修正系数如表所示(由于在计算边坡单元的三维安全系数时已考虑坡度、坡向等因素,故在地形地貌项中不再考虑)。
ISU=SF3D+RII
(2)
式中:ISU——边坡单元稳定性指数; SF3D——边坡单元三维安全系数;RII——边坡单元稳定性修正指数。具体修正系数如表1所示。
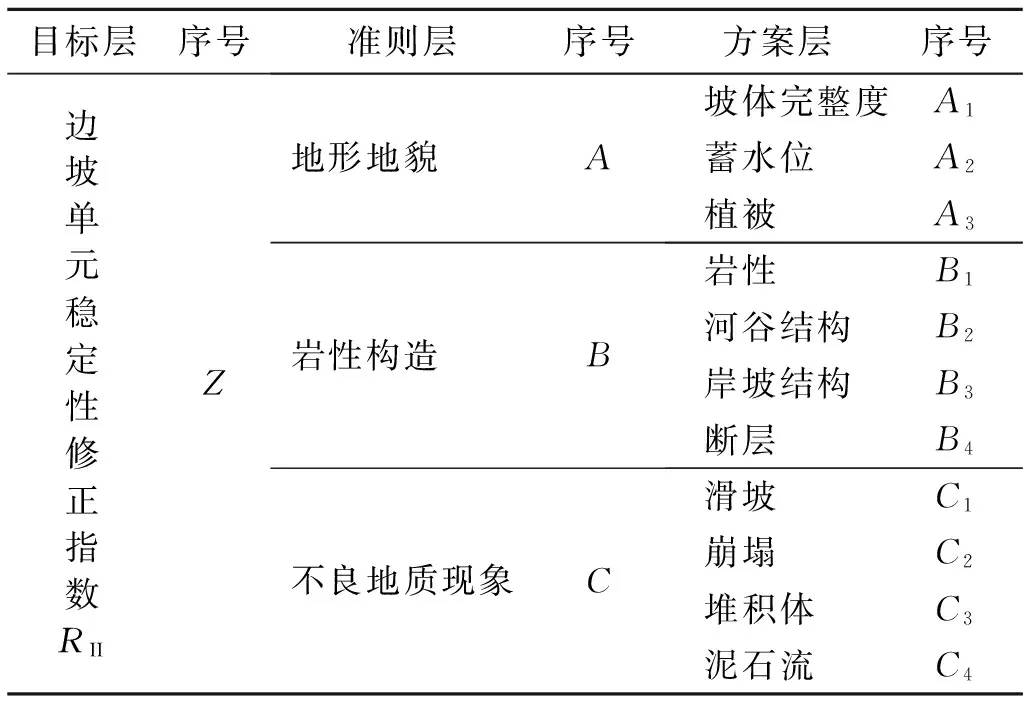
表1 边坡单元稳定性综合评估指标修正系数
建立上述库岸稳定性评价指标后,运用层次分析法的原理,计算边坡单元稳定性指标修正系数各层的指标权重。
对比各指标的相互重要程度,构造判断矩阵如表2所示。

表2 准则层判断矩阵Z
通过计算得出矩阵Z的最大特征值为:
λmax=3.053 6
对应的权向量为:
W=(0.091 4,0.690 9,0.217 7)T
一致性指标:CI=0.026 8
随机一致性指标:RI=0.58
一致性比率:CR=CI/RI=0.0462<0.1CR=CI/RI
通过一致性检验。
1.3.1地形地貌对比各指标的相互重要程度,构造判断矩阵如表3所示。
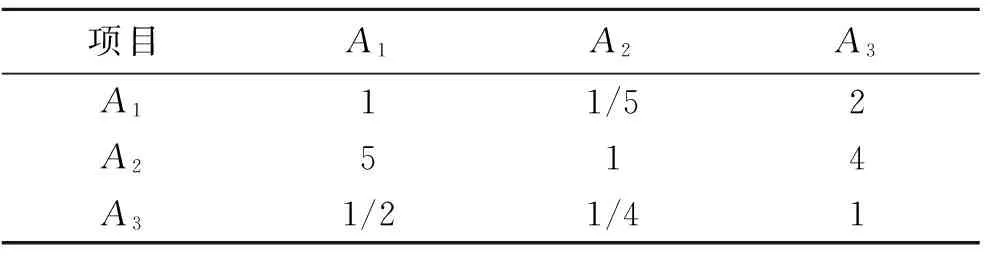
表3 地形地貌判断矩阵A
通过计算得出矩阵A的最大特征值为:
λmax=3.094
对应的权向量为:
W=(0.186 5,0.687 0,0.126 5)T
一致性指标:CI=0.047 0
随机一致性指标:RI=0.58
一致性比率:CR=CI/RI=0.081 0<0.1
通过一致性检验。
相对于目标层,其权向量为:
W=(0.017 0,0.062 8,0.011 6)T
1.3.2岩性构造对比各指标的相互重要程度,构造判断矩阵如表4所示。
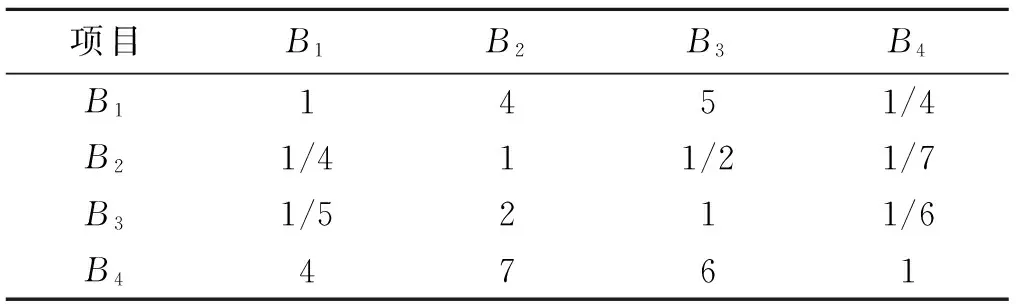
表4 岩性构造判断矩阵B
通过计算得出矩阵B的最大特征值为:
λmax=4.165 1
对应的权向量为:
W=(0.252 8,0.059 7,0.084 3,0.603 2)T
一致性指标:CI=0.069 4
随机一致性指标:RI=0.90
一致性比率:CR=CI/RI=0.077 1<0.1
通过一致性检验。
相对于目标层,其权向量为:
W=(0.174 7,0.041 3,0.005 82,0.416 7)T
1.3.3不良地质现象对比各指标的相互重要程度,构造判断矩阵如表5所示。

表5 不良地质现象判断矩阵C
通过计算得出矩阵C的最大特征值为:
λmax=4.173 8
对应的权向量为:
W=(0.566 9,0.150 7,0.049 7,0.232 8)T
一致性指标:CI=0.057 9
随机一致性指标:RI=0.90
一致性比率:CR=CI/RI=0.064 4<0.1
通过一致性检验。
相对于目标层,其权向量为:
W=(0.123 4,0.032 8,0.010 8,0.050 7)T
通过以上计算,得出各指标的权重如表6所示,对于指标层各指标的取值如表7所示。

表6 边坡单元稳定性综合评估指标修正系数权重
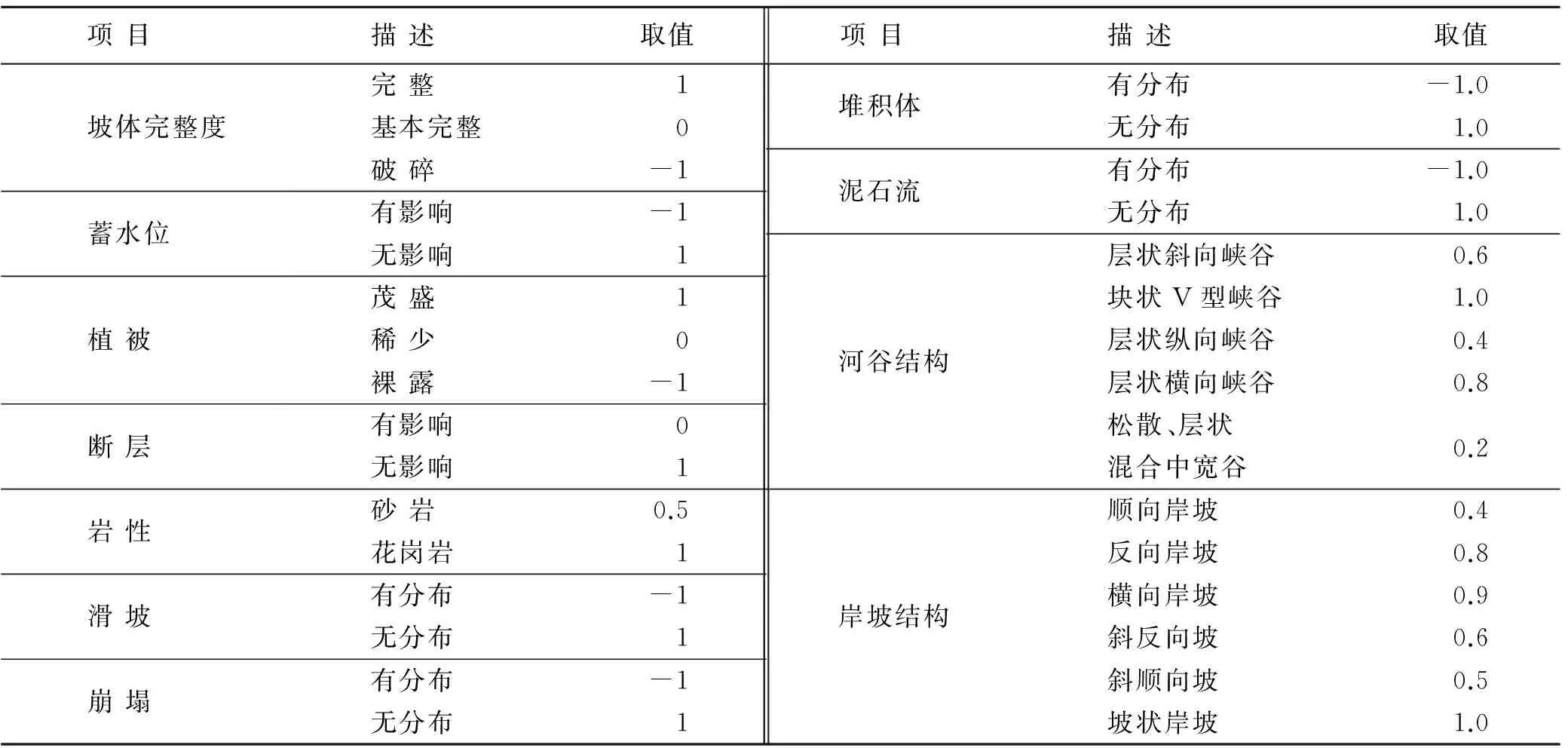
表7 边坡单元稳定性修正指数指标层各项目取值
综上,可定义边坡单元稳定性修正指数RII如式(3)所示,可得边坡单元稳定性指数如式(4)所示。由于边坡单元的稳定指标对库岸段的贡献与其规模正相关,而其规模与面积直接相关,故在得出边坡单元的稳定指标后,可对库岸段的边坡单元的稳定指标进行对面积的加权平均,作为库段的稳定性指标,即岸段稳定性指数如式(5)所示,为方便各库段的比较评判,可把库段稳定性指数标准百分制化,如式(6)所示:
RIIi=∑xiyi
(3)
式中:xi——项目指标值;yi——标值对应权重。
ISUi=SF3Di+RIIi
(4)
(5)
式中:Ai——边坡单元的面积(m2);ISUi——边坡单元的稳定性指数。
(6)
式中:Ii——库岸段稳定性指数;ISi——标准百分制化稳定性指数。
1.4边坡稳定的分析
3D SlopeGIS是基于GIS开发的一个系统插件,可以对某一具体边坡进行综合稳定分析及加固分析,而且可以采用不同的模型计算边坡三维安全系数,同时可以进行最危险滑动面的搜索,此外,在考虑地震、地下水及外荷载等的情况下,研究边坡在各种荷载组合下的三维稳定性。
2结果与分析
2.1研究区库岸分段
由于库岸边坡的稳定性情况与该段的地形地貌、地层岩性、构造和岸坡结构等直接相关,其破坏形式也不一样,如“V”型峡谷与“U”宽谷、沉积岩与侵入岩河段区分明显;顺向坡可能更多的产生滑坡破坏,而反向坡更多的可能是产生崩塌破坏;有断层通过的河段稳定性较差。故可根据以上对地形地貌、地层岩性、构造和岸坡结构等基本地质条件的分析,把研究区分成12段(如附图16所示)。
2.2研究区边坡单元划分
从地形学上看,边坡单元可以用地形上的山脊线和谷底线来划分。采用水文模型工具,经过统合临近要素,得到研究区域边坡单元合理的划分,最终结果如图1所示。结合库岸分段结果,可以得到每一个库段的边坡单元分布情况,本文以第一段的边坡单元(图2)为例详细说明。同时对每个边坡单元进行编号。
2.3研究区边坡单元三维安全系数
得到研究区的边坡单元后,针对每一段的每一个边坡单元进行三维安全系数计算。此处运用3D SlopeGIS边坡三维分析软件中的Janbu[12]模型计算每个边坡单元的三维安全系数。由于研究区域受地下水影响不明显,故在运用3D SlopeGIS计算边坡单
元稳定性时将地下水直接予以考虑,而在运用层次分析方法时不再考虑。此处依然以第一段的边坡单元为例(如表8所示)。
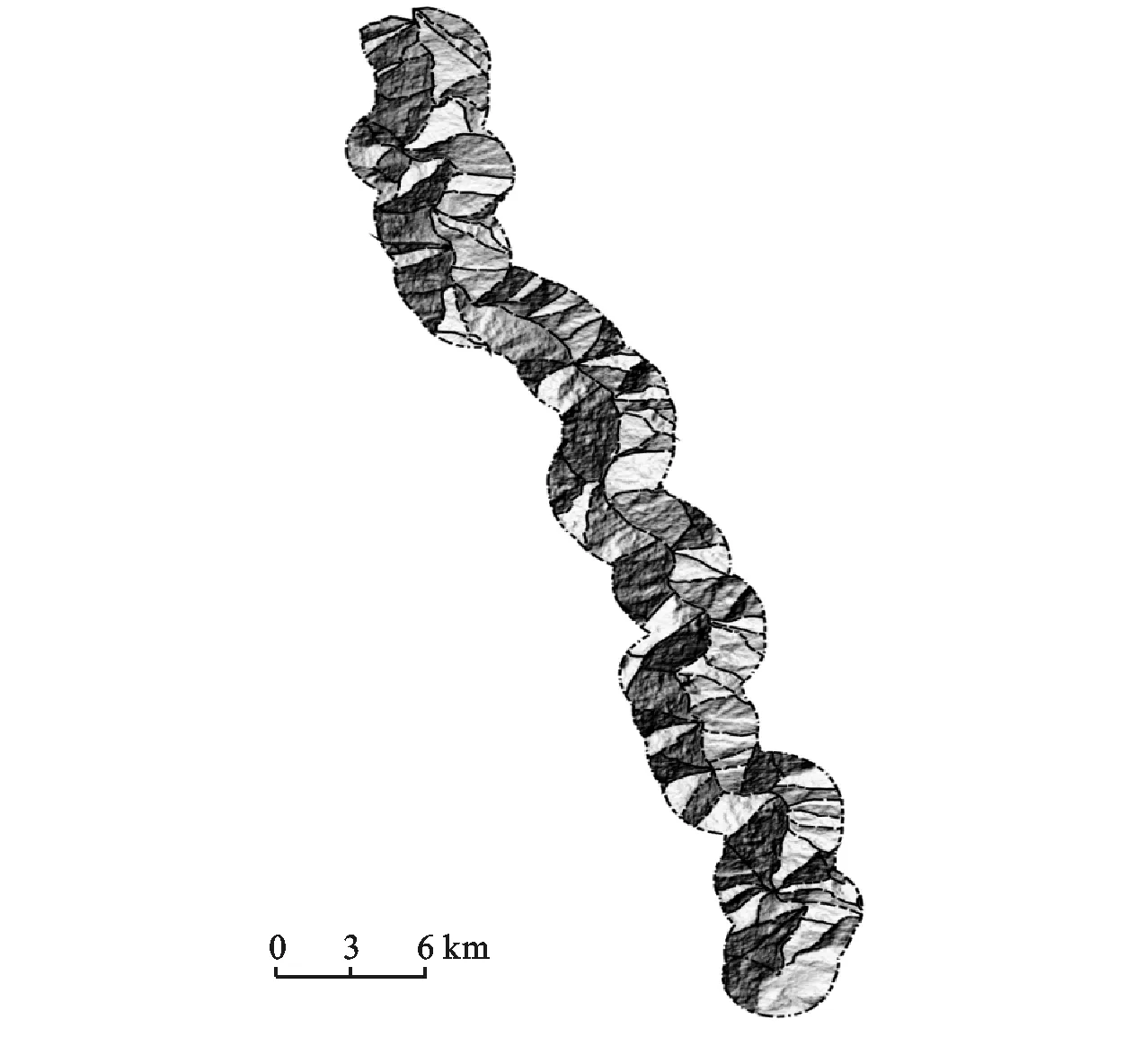
图1 最终的研究区边坡单元(附山体阴影)
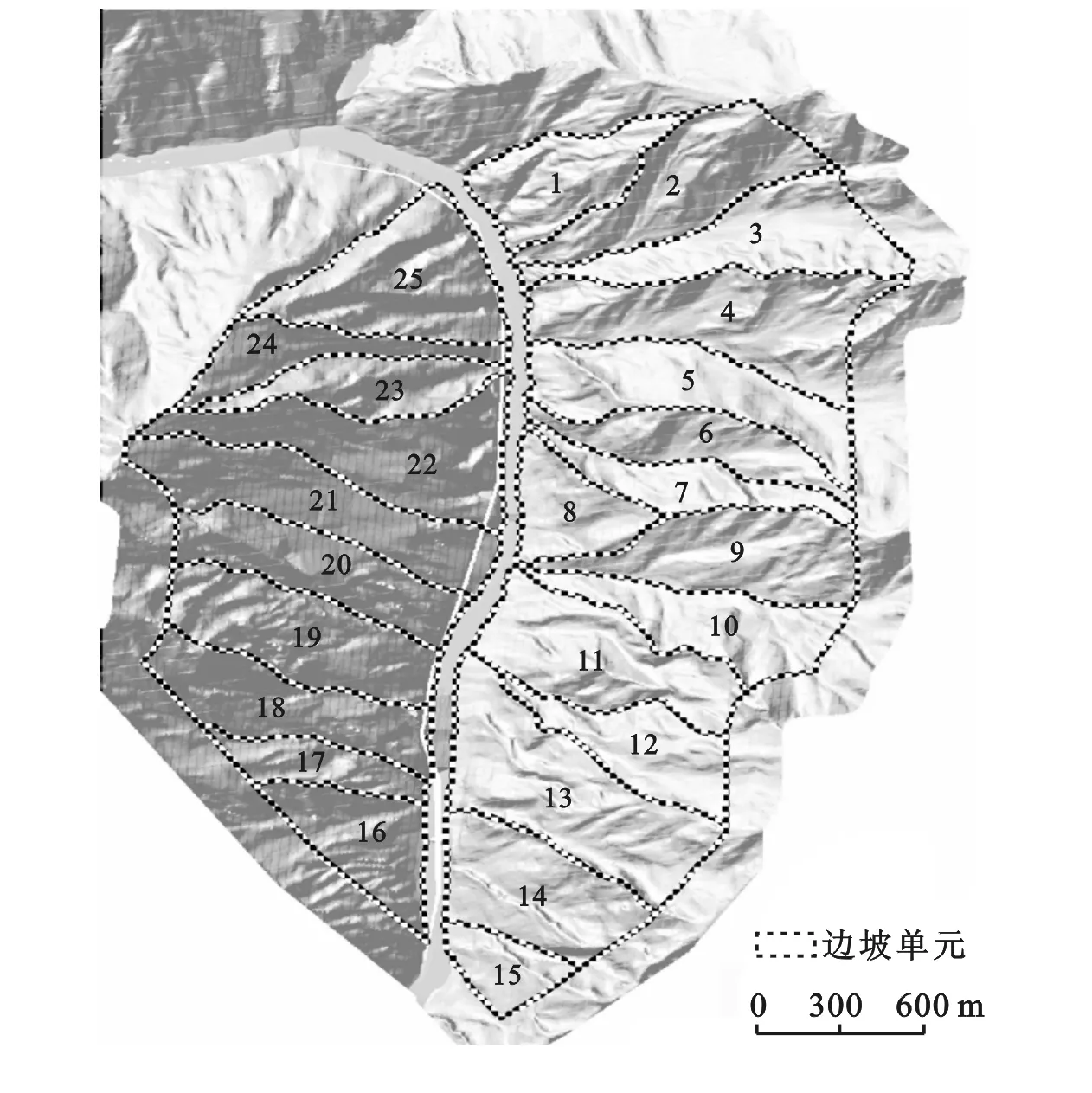
图2 研究区RBS01段边坡单元
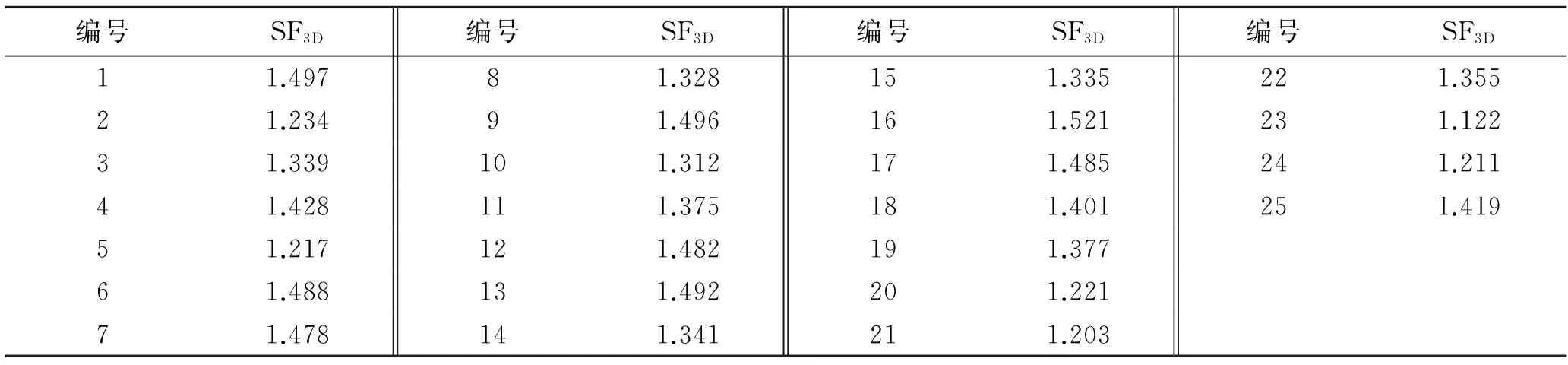
编号SF3D编号SF3D编号SF3D编号SF3D11.49781.328151.335221.35521.23491.496161.521231.12231.339101.312171.485241.21141.428111.375181.401251.41951.217121.482191.37761.488131.492201.22171.478141.341211.203
2.4研究区库岸稳定综合性评价
根据上文定义的边坡稳定性指数,可以计算得到各边坡单元的稳定性指数,同样以第一段的边坡单元为例(如表9所示)。结合第一段各边坡单元的面积(表10),可以得到第一段的稳定性指数。按照同样的步骤,可以得到其余各段的稳定性指数(如表11所示)。
为方便研究区各库段之间的比较评判,把库段稳定性指数标准百分制化后,结果如表12所示。
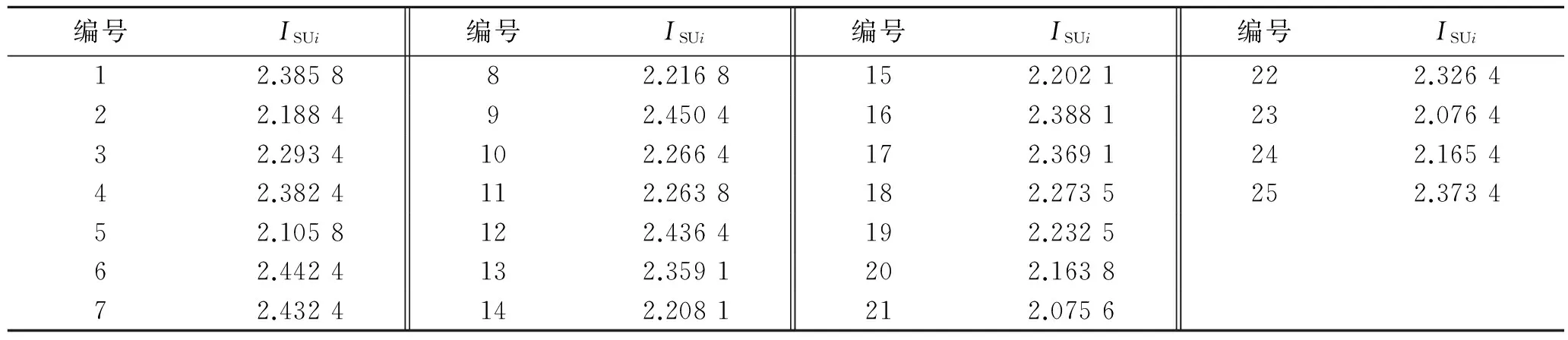
表9 RBS01段各边坡单元的稳定性指数
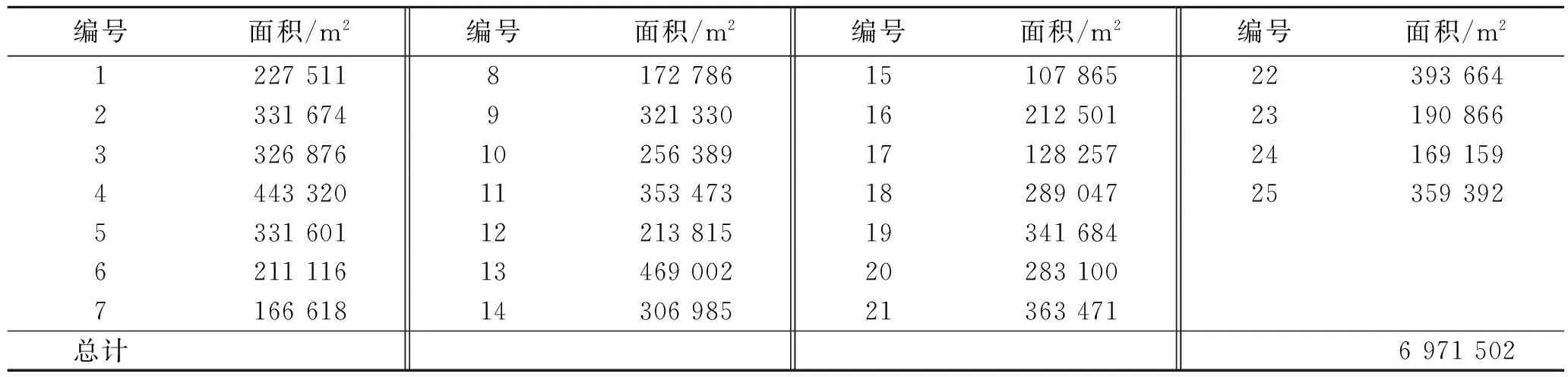
表10 RBS01段各边坡单元面积

表11 各岸坡段的稳定性指数

表12 库岸段标准百分制化指数
按照工程上常用的对库岸稳定性划分的四分法,把库岸的稳定性分成稳定、基本稳定、潜在不稳定和不稳定,定义90(含)分以上为稳定段,80(含)~90分为基本稳定段,70(含)~80分为潜在不稳定段,70分以下为不稳定段。
从表12可以看出,90分以上的库段有RBS05,RBS08;80~90分的库段有RBS01,RBS03,RBS04,RBS06,RBS07,RBS09,RBS12;70~80分的库段为RBS02,RBS10,RBS11。
由以上划分结果可得出库区的稳定段为RBS05,RBS08;基本稳定段为RBS01,RBS03,RBS04,RBS06,RBS07,RBS09,RBS12;潜在不稳定段为RBS02,RBS10,RBS11,无不稳定岸坡,结果如图3所示。
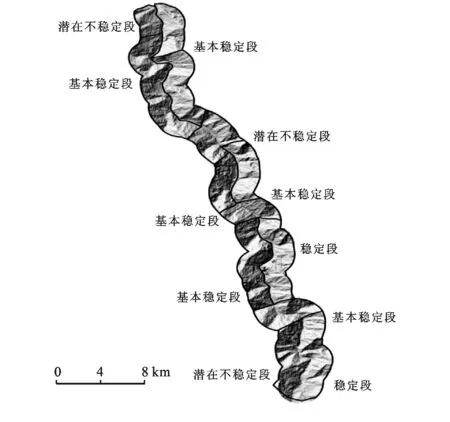
图3 研究区库岸稳定性分段示意图
3讨论与结论
(1) 通过流程化的GIS数据处理方法,可以高效的把多源数据加入地理信息系统数据库,不仅实现了对库区基本地质条件和不良地质现象的解译分析,而且便于与其他平台进行数据的交换。
(2) 通过对库岸稳定性的影响因素分析,将研究区划分为独立的边坡单元,以此作为研究对象,计算其三维安全系数,作为库岸稳定评价的基本指标。
(3) 采用层次分析法,对库岸稳定评价的基本指标予以修正,以此建立了基于边坡单元的定量三维稳定性指标与定性指标相结合的库岸稳定性层次分析评价方法。
稳定性评价指标体系的建立包括评价指标的选择及指标量化两方面的内容,这两方面的选取均需要具有丰富的专业知识和现场经验,本文部分指标的选取和取值有待进一步的商榷。结合现场的情况来看,最后的稳定程度评价结果基本符合实际情况。
[参考文献]
[1]中华人民共和国国家发展和改革委员会.DL/T5336—2006水电水利工程水库区工程地质勘察技术规程[S]. 2006.
[2]地质矿产部编写组.长江三峡工程库岸稳定性研究[M].北京:地质出版社,1988.
[3]Luino F. Sequence of instability processes triggered by heavy rainfall in the northern Italy [J]. Geomorphology, 2005,66(1):13-39.
[4]仵彦卿.地下水与地质灾害[J].地下空间与工程学报,1999,19(4):303-310.
[5]马水山,雷俊荣,张保军,等.滑坡体水岩作用机制与变形机理研究[J].长江科学院院报,2005,22(5):37-39.
[6]王思敬,马凤山,杜永廉.水库地区的水岩作用及其地质环境影响[J].工程地质学报,1996,4(3):1-9.
[7]刘新喜,夏元友,张显书,等.库水位下降对滑坡稳定性的影响[J].岩石力学与工程学报,2005,24(8):1439-1444.
[8]朱冬林,任光明,聂德新,等.库水位变化下对水库滑坡稳定性影响的预测[J].水文地质工程地质,2002,29(3):6-9.
[9]Lane P A, Griffiths D V. Assessment of Stability of Slopes under Drawdown Conditions[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2000,126(5):443-450.
[10]孙宏才,田平,王莲芬.网络层次分析法与决策科学[M].北京:国防工业出版社,2011.
[11]谢谟文,蔡美峰.信息边坡工程学的理论与实践[M].北京:科学出版社,2005.
[12]Janbu N. Slope stability computations[C]∥Embankment-Dam Eng., Publication of Wiley & Sons Incorporated, New York, 1973:47-86.
收稿日期:2015-05-13修回日期:2015-07-13
通讯作者:胡嫚(1988—),女(汉族),贵州省毕节市人,博士,讲师。主要从事地质灾害调查研究、岩土工程数值模拟、防灾减灾的研究及教学工。E-mail:humanyyyes@126.com。
文献标识码:A
文章编号:1000-288X(2016)03-0290-07
中图分类号:P642.2
Slope Unit-based Application of Analytic Hierarchy Process in Stability Evaluation of Reservoir Bank
XU Bo1, XIE Mowen1, HE Xingdong2, HU Man3
(1.CollegeofGivilandEnvironmentalEngineering,UniversityofScienceandTechnologyBeijing,Beijing100083,China; 2.PowerchinaKunmingEngineeringCorporationLinited,Kunming,Yunnan650051,China; 3.CollegeofEngineeringandTechnology,SouthwestUniversity,Chongqing400715,China)
Abstract:[Objective] To analyze the influence factors of the Mengdigou reservoir bank stability in order to provide new train of thought to evaluate the stability of reservoir bank. [Methods] On the basis of the analysis of the engineering geological conditions and the interpretation of unfavorable geological phenomenon, this paper classified the bank into different segments. Then using the principle of the slope unit, we then taken these segments as independent research objects and analyzed the factors affecting the bank stability. And then we used three-dimension factor safety of slope units as an index of the stability evaluation and used analytic hierarchy process(AHP) to analyze the factors affecting slope stability. Finally we established hierarchy analysis and evaluation methods for the stability of reservoir bank based on the slope unit. [Results] The method was tested in the engineering practice, showing that the method is reliable and practical. [Conclusion] Tanking the slope unit as the research object, using the AHP can effectively analyze the stability of reservoir bank, which can support the decision of project.
Keywords:stability of reservoir bank; remote sensing; slope unit; analytic hierarchy process; three dimensional analysis
资助项目:国家自然科学基金项目“高山峡谷水库区区域滑坡早期动态识别研究”(41372370)
第一作者:许波(1986—),女(汉族),安徽省淮南市人,博士研究生,主要研究方向为边坡稳定性、滑坡安全监测。E-mail:xuboustb@163.com。

