轴向载荷下高速角接触球轴承运动特性分析

汪杨，陈国定，李德水，余永健

(西北工业大学 机电学院，西安 710072)

随航空航天技术的发展,发动机日益朝着大推重比方向发展，关键是提高航空发动机主轴轴承的dm·n值。随dm·n值的增大，轴承运转过程中滚动体与内圈之间会出现严重的打滑和磨损，且滚动体与保持架之间的频繁碰撞也会影响轴承工作稳定性，甚至引起保持架断裂失效，这些现象对于航空发动机用高速轴承尤为突出，故需建立能够真实反映轴承运转的力学模型。

国外对高速角接触球轴承的性能分析始于20世纪60年代。文献[1]提出了滚道控制理论，建立了轴承拟静力学分析模型，但该模型未考虑弹流润滑的作用；文献[2]结合弹流润滑理论进一步发展了滚动轴承的拟静力学模型，弥补了Jones模型的不足。然而由于轴承拟静力学模型并未考虑保持架的作用，存在着自由度少、计算精度低的问题，不能真实反映轴承的实际运转情况。文献[3-4]修正和发展了Harris模型，建立拟动力学模型对轴承主要零件进行分析，能够真实反映轴承的实际运转情况，但仍无法满足轴承实际运转过程，特别是瞬态过程模拟的要求。在拟动力学模型的基础上，文献[5-6]先后建立了轴承动力学分析模型，用来描述轴承实际状况。

国内学者近些年也对高速角接触球轴承的动力学进行了研究。文献[7-8]建立了高速角接触球轴承拟静力学模型，在此基础上开展了航空发动机高速球轴承力学特性的分析与研究；文献[9]对仅受轴向载荷的高速球轴承进行了拟动力学分析以掌握滚动零件的运动特性，重点研究了轴向载荷对轴承运动参数和疲劳寿命的影响；文献[10]在此基础上建立了能够承受联合载荷的轴承拟动力学模型，并以航空高速轴承为例，分析了结构参数和工况参数对滚动轴承旋滚比和PV值等动态特性的影响规律；文献[11]建立了简化的动力学模型，仅对保持架的位移及质心位置进行了分析。

国内对轴承动力学的研究仍存在一些问题，例如：忽略因球公转速度差异引起的切向惯性力从而使分析模型过于简化；当滚动体在接触区滑动速度较大时，润滑剂不再是Newton流体，而大多数拖动力模型仍以Newton流体计算滚动体的油膜拖动力，从而产生误差；均在一定程度上使高速滚动轴承动力学的分析结果与实际情况有较大误差。此外，轴承动力学微分方程组更为复杂且更具非线性特征，故需探求有效的求解方法。

现以主要承受轴向载荷的航空涡轴发动机转子的角接触球轴承为例，在拟动力学模型的基础上，建立了比较完善的高速角接触球轴承动力学模型，列出了钢球、保持架和内圈的动力学微分方程组，并采用四阶Runge-Kutta法对3个微分方程组进行积分求解，获得了钢球自转角速度、保持架位移以及内圈位移随时间的变化规律。该研究不仅为航空用高速角接触球轴承动力学性能分析提供了帮助，也为轴承-机械转子系统的动力学分析奠定了基础。

1 数学模型的建立

1.1 钢球动力学微分方程组

轴承中第j个钢球的受力情况如图1所示，根据钢球所受合力和合力矩确定的钢球动力学微分方程组为

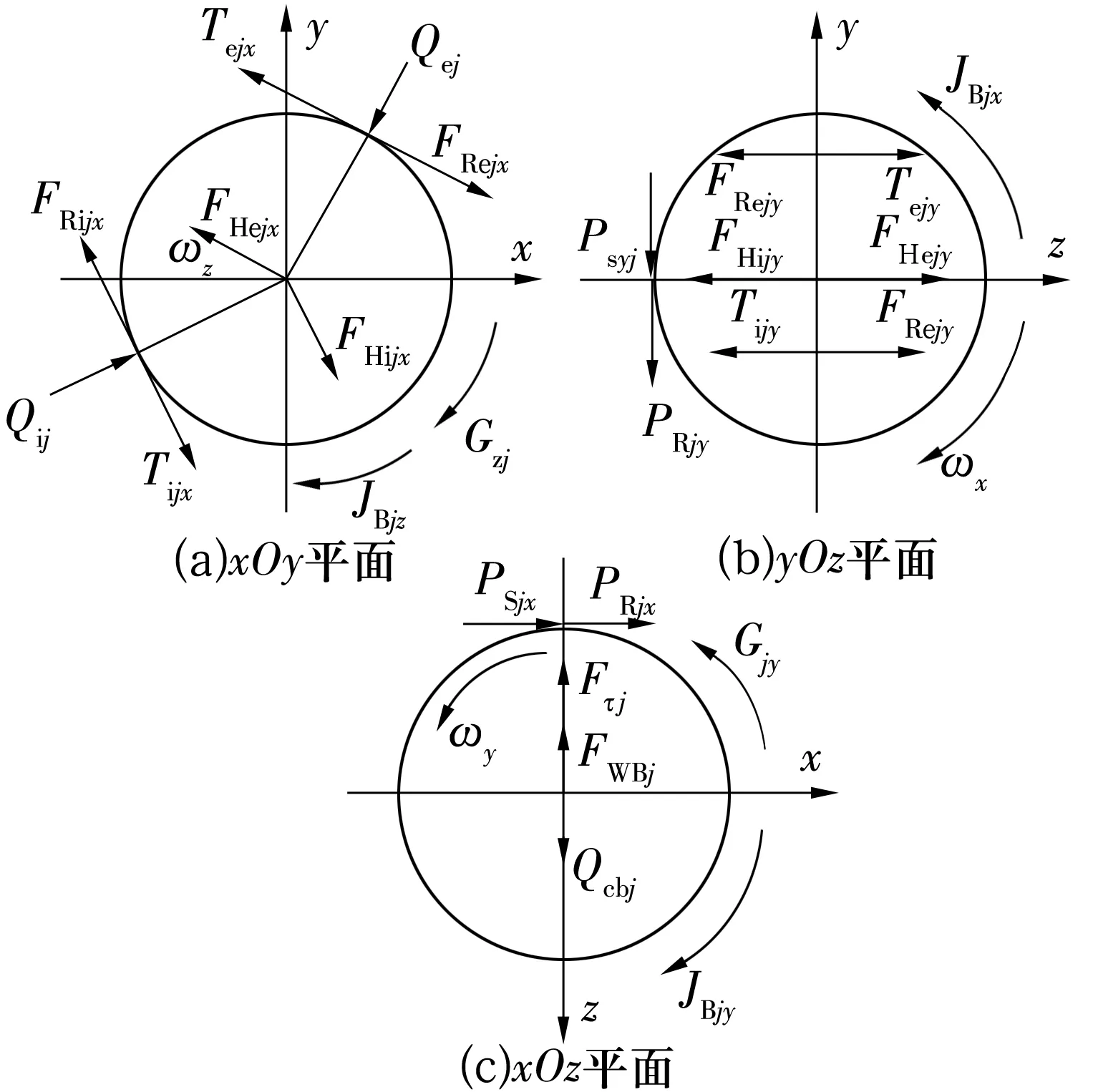
图1 钢球受力分析图

(1)

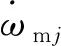
1.2 保持架动力学微分方程组

根据保持架和套圈的几何特点，保持架受力情况如图2所示，保持架动力学微分方程组为

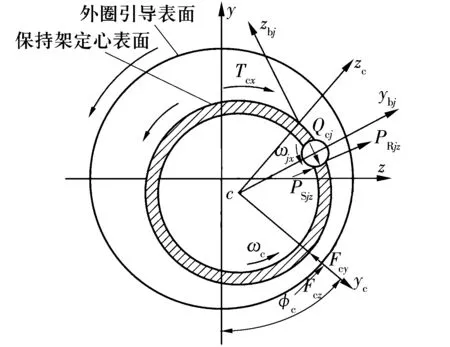
图2 保持架受力分析图

,(2)

1.3 内圈动力学微分方程组

根据内圈与钢球及保持架之间的相互作用，内圈动力学微分方程组为

,(3)

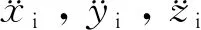
2 模型求解及关键技术

高速角接触球轴承动力学模型的计算流程图如图3所示，动力学模型求解关键点如下：

图3 高速角接触球轴承动力学分析流程图

1)动力学模型求解初值由拟动力学计算获得，即在相同结构参数和工况参数下，对高速角接触球轴承进行拟动力学模型计算，获得钢球的公转、自转角速度在x，y，z方向的分量,钢球与内外圈的接触角,保持架位移以及内圈位移的收敛值，为初次计算钢球与套圈沟道和保持架之间的相互作用力、保持架与内圈之间的相互作用力以及轴承零件与润滑油之间的流体动压力做准备。此后，以上各力均由动力学积分求解。

2)由于动力学模型将轴承零件的加速度转化成时间ti的函数，求解时需要设定最终的循环截止时间tmax，因此不需要考虑平衡收敛问题。

3)对于动力学模型，采用自适应步长Δti的四阶Runge-Kutta法对钢球、保持架及内圈微分方程组进行积分求解。

3 动力学模型计算结果

采用的角接触球轴承的相关参数见表1，润滑油密度为952.52 kg/m3，黏度为0.027 6 Pa·s，黏压系数为1.55×10-8m2/N，热传导系数为0.096 6 W·m-2·k-1，油气比为0.2，保持架引导方式为外圈引导。

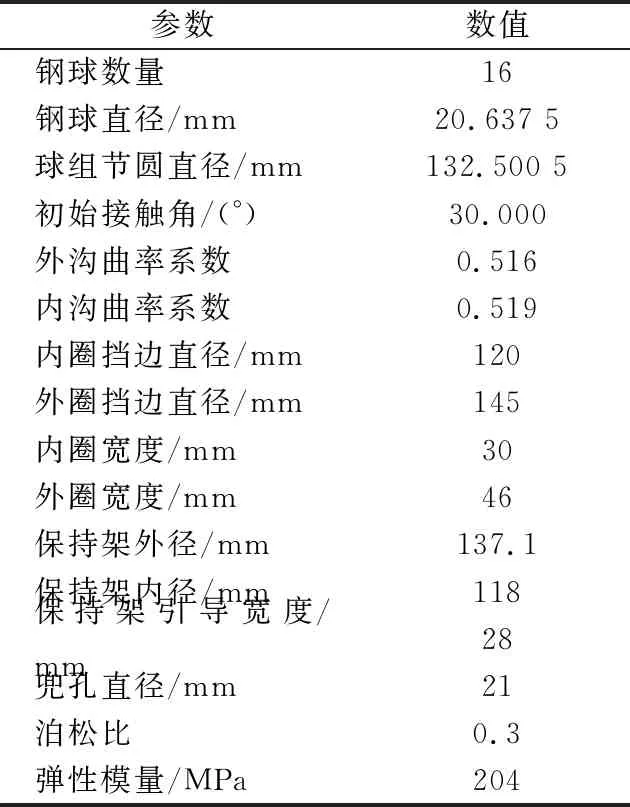
表1 轴承相关参数

3.1 钢球自转角速度

在转速n=12 000 r/min时，钢球在x，y,z方向的自转角速度随轴向载荷的变化如图4所示，力方向的确定是假设钢球的自转角速度为正。最终得到的自转角速度为负值说明运转方向与假设相反。由图可知，随轴向载荷增加，钢球与套圈之间的法向接触力随之增加,钢球x，y,z方向的自转角速度逐渐减小。

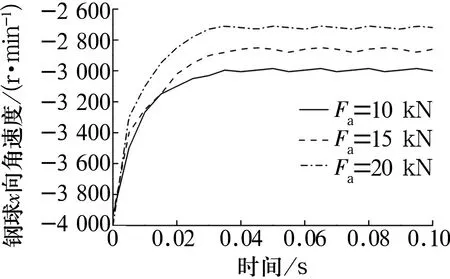
(a)x方向

在轴向载荷Fa=10 kN时，钢球x，y,z方向的自转角速度随转速变化如图5所示。由图可知，随内圈转速增加，钢球x，y，z方向的自转角速度随之增大。

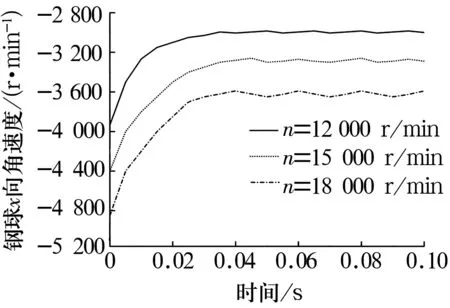
(a)x方向

3.2 保持架位移

在轴向载荷Fa=10 kN时，保持架y,z方向的位移随转速的变化情况如图6所示。由图6可知，随转速增加，钢球与保持架间的碰撞加剧，导致保持架y，z方向的位移逐渐增加。

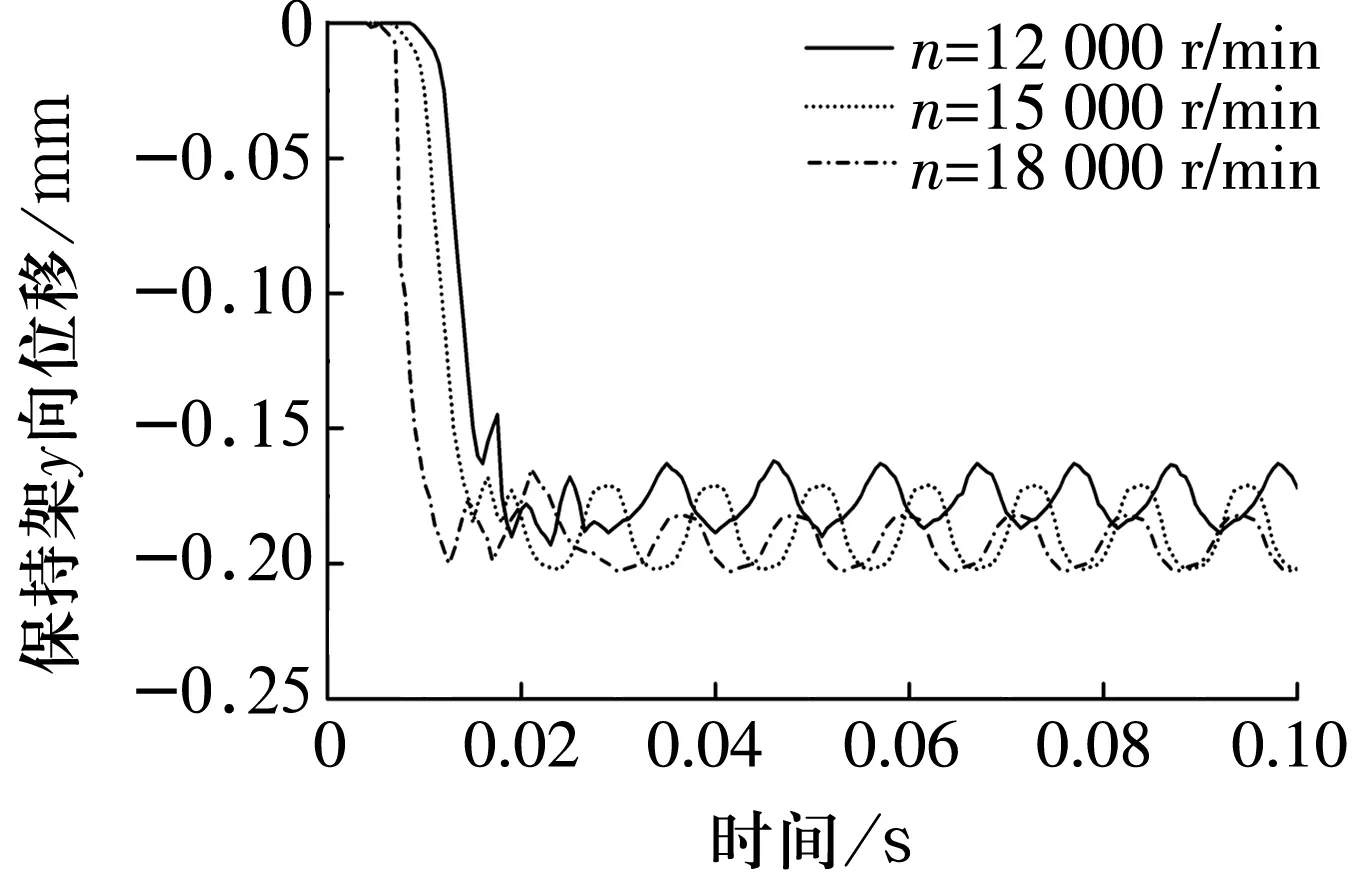
(a)y方向

3.3 内圈位移

在转速n=12 000 r/min时，内圈x，y方向位移随轴向载荷变化如图7所示。由图可知，随轴向载荷增加，钢球与内圈之间的法向接触力变大，内圈变形也增大，造成内圈x,y方向的位移增加。

(a)x方向

在轴向载荷Fa=10 kN时，内圈x，y方向的位移随转速的变化如图8所示。可以看出，随转速增加，钢球的离心力变大 ，钢球在离心力作用下的“外抛”加剧，使钢球与内圈之间的法向接触力减小，内圈x方向的位移减小，内圈y方向的位移增大。

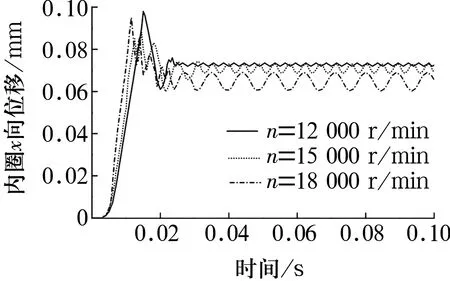
(a)x方向

4 动力学模型和拟动力学模型计算结果的比较

国内外对轴向载荷下高速角接触球轴承的动态性能分析缺少完善的研究成果，为此，对动力学和拟动力学的分析结果对比，定量获得拟动力学和动力学模型计算的差别。在2个模型中，角接触球轴承的相关参数相同,轴向载荷为10 kN，转速为12 000 r/min。保持架的引导方式为外圈引导。

4.1 钢球自转角速度对比

采用动力学和拟动力学模型计算获得的钢球自转角速度在3个方向上的分量如图9所示。可以看出，采用拟动力学模型计算出的钢球自转角速度3个方向分量与时间没有关系，而采用动力学模型计算出的钢球自转角速度3个方向分量随时间发生变化，一段时间后钢球自转角速度的动力学计算结果趋于稳定。此外，稳定后的钢球自转角速度动力学与拟动力学计算结果在数值上有差别。

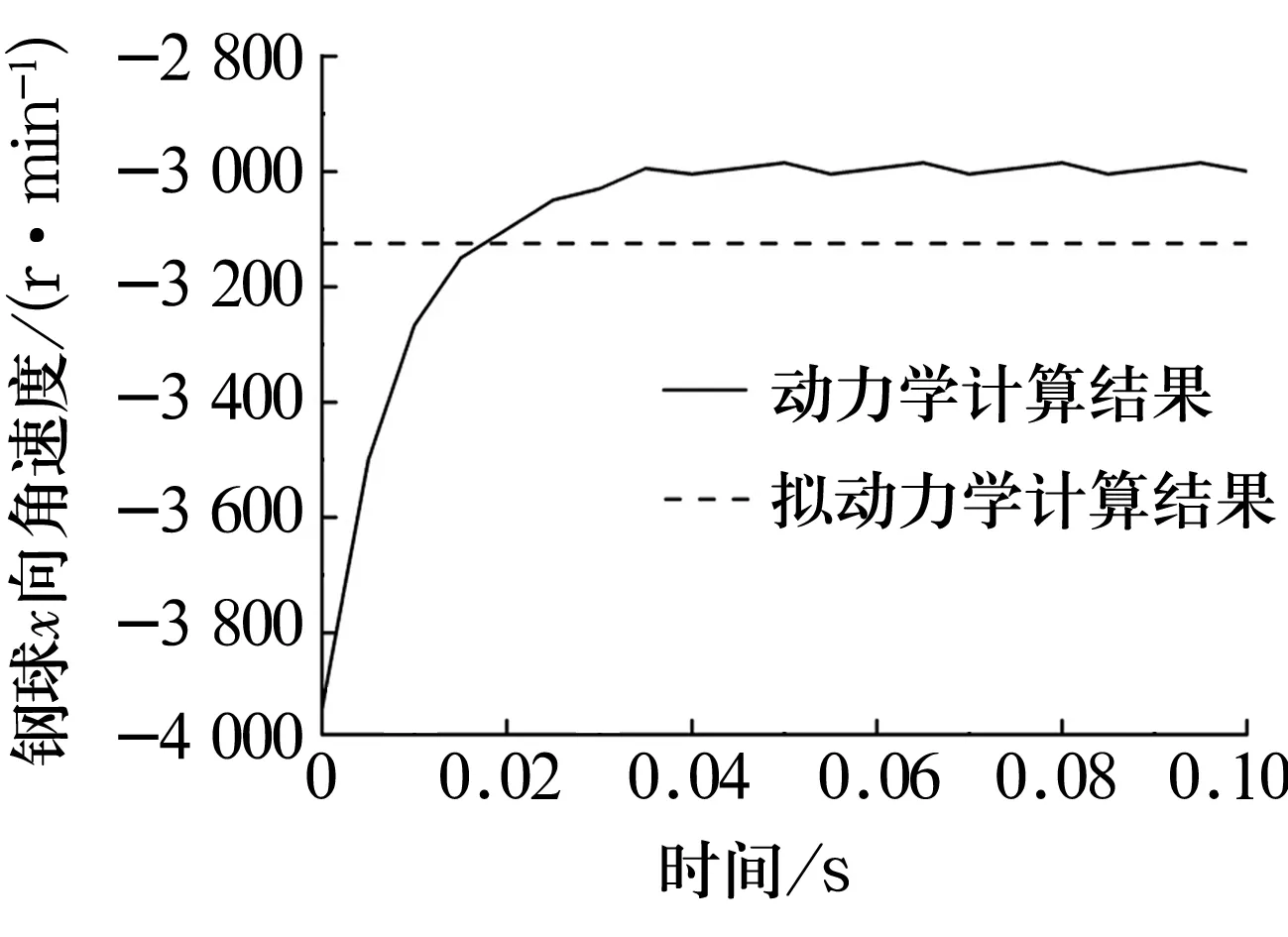
(a)x方向

4.2 保持架位移对比

采用动力学和拟动力学模型计算获得的轴承保持架在y，z方向位移如图10所示。采用拟动力学模型计算出的轴承保持架位移与时间没有关系，而采用动力学模型计算出的轴承保持架位移随时间发生变化，一段时间后，位移的动力学计算结果在平均意义上趋于稳定，但仍然存在幅值不大的波动现象。稳定后的轴承保持架位移动力学与拟动力学计算结果在数值上有差别。

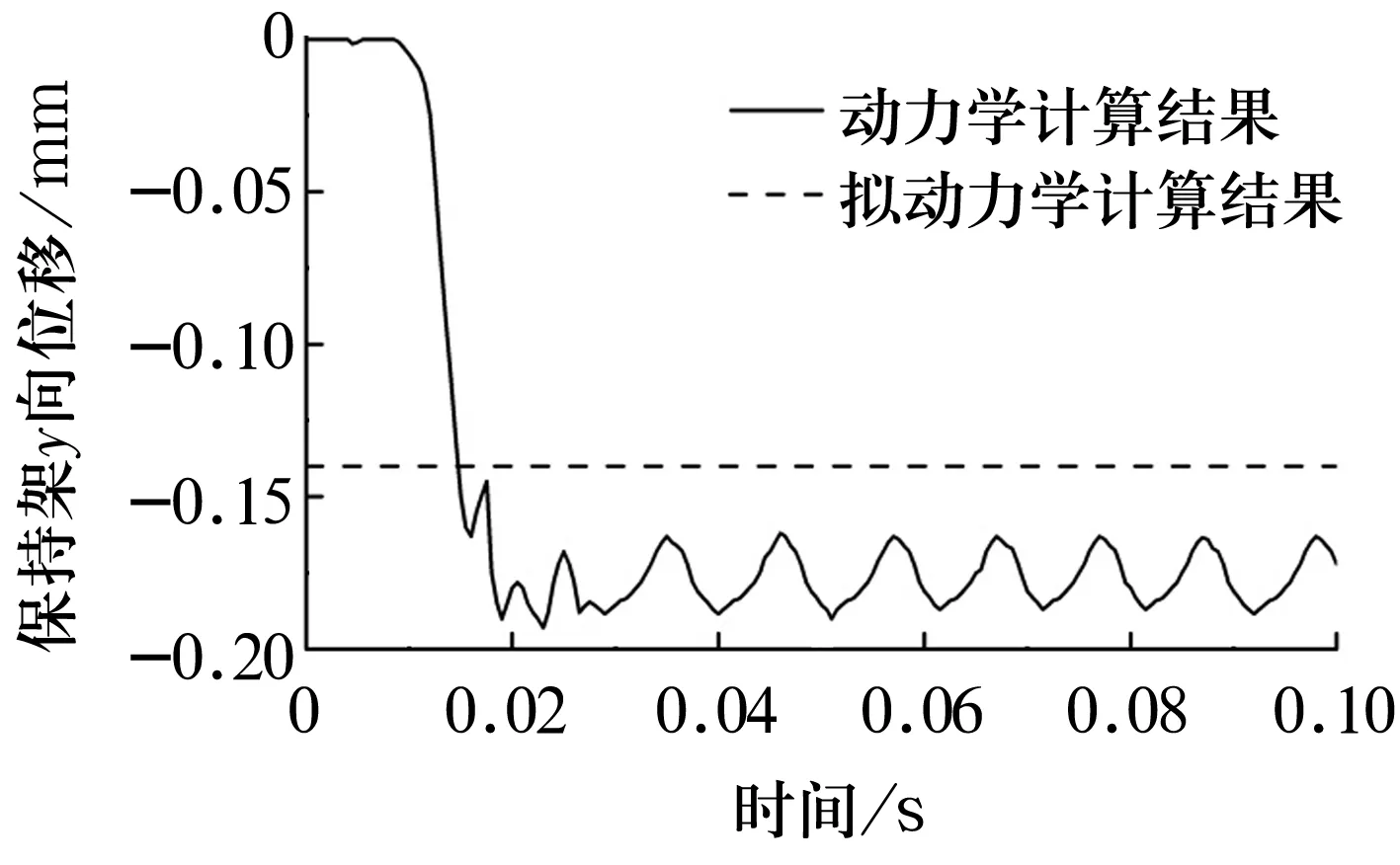
(a)y方向

4.3 内圈位移对比

采用动力学和拟动力学模型计算获得的轴承内圈在x,y方向位移如图11所示。采用拟动力学模型计算出的轴承内圈位移与时间没有关系，而采用动力学模型计算出的轴承内圈位移随时间发生变化，并最终趋于稳定，不过在数值上仍存在幅值不大的波动。稳定后的轴承内圈位移动力学与拟动力学计算结果在数值上有差别。

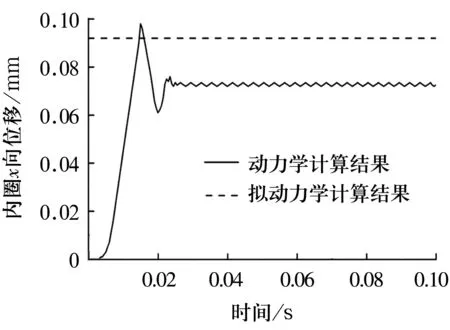
(a)x方向

5 结论

1)轴承的轴向载荷直接影响其动态性能，过高的轴向载荷虽然使钢球的自转角速度减小，降低钢球的公转打滑率，但同时会增大内圈的位移，不利于轴承运行的平稳性。故角接触球轴承在实际工况下应该承受适当的轴向载荷。

2)轴承转速同样会直接影响其动态性能，随转速增加，钢球的自转角速度和保持架的位移增大，内圈x方向的位移逐渐减小，内圈y方向的位移逐渐增加，过高转速不利于轴承运行的平稳性，故应该在满足工作条件的基础上，尽量选取较低的轴承转速。

(3)与拟动力学结果相比，根据求解动力学方程得到的钢球转速、保持架位移和内圈位移并不是一个常量，而达到稳定后，随时间变化存在很小的波动，并且波动的平衡位置与拟动力学结果在数值上存在略微差别。