竖直振动下颗粒物质的行为模式研究进展

刘举，白鹏博，凡凤仙，胡晓红（上海理工大学能源与动力工程学院，上海 00093；上海理工大学上海市动力工程多相流动与传热重点实验室，上海 00093）



综述与专论

竖直振动下颗粒物质的行为模式研究进展

刘举1,2，白鹏博1,2，凡凤仙1,2，胡晓红1,2
（1上海理工大学能源与动力工程学院，上海 200093；2上海理工大学上海市动力工程多相流动与传热重点实验室，上海 200093）

摘要：竖直振动下颗粒物质行为模式的研究对化工过程中效率的提升具有重要意义，该研究近年来成为热点，并不断取得新进展。本文将已有竖直振动下颗粒物质行为模式研究归纳为：竖直振动颗粒床中颗粒的行为、竖直振动颗粒床中颗粒沿直管的爬升、竖直振动U形管中颗粒的迁移、静止颗粒床中颗粒沿竖直振动管的爬升，并对相关研究进展进行评述，发现目前对颗粒物质运动规律的认识还不深入，颗粒物质行为模式的内在机理上尚存争议。鉴于离散元方法（DEM）能够获得每一个颗粒的运动信息，从而很好地反映颗粒过程的机理和特性，对竖直振动U形管和竖直振动管中颗粒物质行为模式进行DEM模拟再现；据此提出在今后的研究中应充分发挥DEM的优势，深入研究颗粒行为模式的动力学本质和影响颗粒行为模式的因素，为颗粒输运过程的优化提供理论基础和方法指导。

关键词：竖直振动；颗粒物质；行为模式；离散元方法

颗粒物质是指大量离散的固体颗粒相互作用而组成的复杂体系，作为一种特殊的物质形态，其具有迥异于固态、液态与气态物质的行为特性[1]。这类物质广泛存在于能源、材料、制药等化工前沿领域，其在不同几何形状的容器或管道内的流动对于化工过程效率的提升非常重要。将竖直振动引入颗粒系统时，受系统构成的影响，颗粒物质表现出许多奇特的运动规律，如隆起[2]、迁移[3]、爬升[4]，同时伴随颗粒对流[5]、表面波[6-7]等。尽管竖直振动下颗粒物质行为模式的研究已有很长的历史，但由于所研究问题的复杂性和所涉及现象的多样性，目前对颗粒行为模式机理的认识仍不够，受实验手段和测量仪器的限制，颗粒行为模式的机理问题也难以通过实验得到完全解决。基于离散元方法（discrete element method，DEM）的数值模拟将颗粒物质看作由一系列离散的独立运动的单元（颗粒）所组成，每个单元的运动受经典运动方程控制，颗粒物质整体的演变由各单元的运动和相互位置确定。这种方法可以从颗粒尺度上考察相关量的变化，能够很好地反映颗粒过程的机理和特性，是对实验的有力补充。本文将对竖直振动下颗粒物质行为模式的研究进行归纳和评述，并基于DEM对竖直振动U形管和插入静止颗粒床的竖直振动管中颗粒的行为模式进行数值模拟再现，进而指出竖直振动下颗粒物质行为模式研究的发展趋势和研究思路。

1 竖直振动下颗粒物质的行为模式

已有研究中的竖直振动下颗粒物质行为模式可归纳为：竖直振动颗粒床中颗粒的行为、竖直振动颗粒床中颗粒沿直管的爬升、竖直振动U形管中颗粒的迁移、静止颗粒床中颗粒沿竖直振动管的爬升。以下分别进行评述。

1.1 竖直振动颗粒床中颗粒的行为

竖直振动颗粒床中颗粒行为的研究可以追溯到1831年FARADAY[8]在竖直振动的圆筒形容器内观察到颗粒的隆起，以及同时伴随的壁面邻近区域颗粒下降、中心区域颗粒上升的对流现象。然而，这种现象真正引起科研工作者的兴趣却是在最近二十多年。1993年，PAK和BEHRINGER[7]实验研究了环形沙粒层在竖直振动下的行为，发现了颗粒表面逆重力波的存在。随后，在竖直振动的圆筒形容器内，研究者观察到颗粒表面出现的方形和条纹形斑图[9]，以及锥状尖峰和凹坑[10]。在对竖直振动矩形槽内颗粒行为模式研究中，1995年，陈伟中[11]观察到颗粒的隆起和对流；1996年，AOKI等[12]观察到与 FARADAY[8]实验方向相反的颗粒对流模式，即壁面附近颗粒上升而中心区域颗粒下降，并探讨了颗粒对流模式的转变特性。JAEGER等[13]分析了引起竖直振动床内颗粒物质隆起和对流的器壁摩擦和间隙气体作用机理。前者认为靠近壁面的颗粒由于壁面摩擦作用会随壁面快速运动，而中心区域的颗粒运动速度较低，因此形成了对流，然而该机理无法解释消除器壁摩擦时的颗粒对流现象；后者认为容器向下运动时颗粒与容器底分离，形成间隙，气体沿边壁进入底部间隙并流向容器中心，气体曳力使得近壁颗粒下降的同时向容器中心移动，从而容器中心区域颗粒增多；当颗粒与容器底相接触时，近壁颗粒首先与容器底接触，间隙气体被压缩而对颗粒产生向上、向外的曳力，此时近壁颗粒由于已被压实而无法向外移动，因而颗粒在容器中心形成隆起。1997年，CERDA等[14]对竖直振动下颗粒物质的表面波进行分析，指出颗粒表面斑图形成的机理是颗粒的自聚集效应和扩散效应之间的竞争。1997年，CHEN等[15]实验研究了竖直振动窄长容器内颗粒的隆起和对流，发现器壁摩擦和间隙气体对隆起和对流作用较小，从而提出了自放大作用机理。自放大作用机理认为由于振动起始时刻颗粒空间分布不均匀，颗粒表面存在微小隆起，微小隆起下方颗粒较之周围颗粒受到更大的压力，导致容器向下运动时最底部的颗粒层与容器分离后呈下凸形，同时隆起中心区域颗粒发生膨胀，引起两侧颗粒向隆起位置迁移；当容器底与颗粒接触时，隆起位置底部最先与容器底接触，促使隆起增大。虽然自放大作用机理可以解释隆起的形成、隆起中心的随机性、小隆起合并为大隆起等实验现象，但并不能因此确定自放大是形成隆起的唯一机理。对比自放大与间隙气体作用机理，发现两种机理都认为当颗粒与容器底分离时颗粒由两侧向隆起中心移动，但在对颗粒与容器底接触过程的认识上却存在分歧。自放大机理认为隆起底部中心位置颗粒最先与容器底接触；而间隙气体作用机理却认为近壁颗粒最先与容器底接触。之后，RAPAPORT[6]与LEE[16]对竖直振动床中颗粒的行为进行了二维分子动力学模拟，分析了表面波的形成和特性。2001年，SUI等[17]实验研究了振动频率和振动强度对表面波和斑图的影响；WI等[18]实验发现双频振动下颗粒表面将出现更为丰富的斑图，如方形、六边形、扭曲平面等。2005年，WONG等[19]利用中子发射技术跟踪竖直振动颗粒床中示踪颗粒的运动，得到了典型位置颗粒的位移曲线。2007年，ESHUIS等[5]给出了竖直振动颗粒床中颗粒物质行为（如弹跳、起伏、Leidenforst效应、对流卷等）的相图；VAN GERNER 等[2]基于颗粒动力学-计算流体力学模拟，再现了FARADAY[8]的实验现象，验证了隆起和对流的间隙气体作用机理。2010年，孔维姝等[20]实验研究了竖直振动下准二维矩形容器内颗粒的对流受振动条件和容器尺寸的影响规律。2013年，李芳芳等[21]提出应力波作用机理，从一个新的视角对颗粒对流进行了解释。应力波作用机理认为不同区域颗粒的振动是不协调的，一个振动周期内存在压缩波、松弛波和重力波，重力波的作用使得颗粒向容器中心发生横向位移，打破颗粒周而复始的上升下降，从而产生对流；该机理可以解释壁面邻近颗粒下降、中心区域颗粒上升的对流，但不能解释反向的对流。2014年，YAMADA和KATSURAGI[22]通过实验和理论分析获得了竖直振动床中颗粒的量纲为1对流速度与量纲为1振动参数、量纲为1系统尺寸的函数关系，可用于粗略估算对流速度，使得对流的描述有了量化的基础；ZHANG等[23]对竖直振动床中颗粒对流特性进行实验研究，发现振动频率对对流卷的个数和方向有重要影响，而振动强度主要影响对流卷的大小和强度。此外，一些研究者还对竖直振动床中颗粒的堆积密度[24]、能量耗散[25-26]以及颗粒对容器底冲击力的倍周期分岔现象[27-29]等进行了研究。可见，振动颗粒床中颗粒物质的行为模式（图1）研究已产生了诸多成果，如认识到斑图的多样性，并用颗粒的自聚集和扩散效应对斑图的形成进行解释，对隆起和对流进行了较多研究，提出了隆起和对流的器壁摩擦、间隙气体、自放大、应力波作用机理，建立了对流速度的量纲为1关系式；然而，已有研究集中在通过实验研究颗粒物质的宏观行为，缺乏对颗粒微观动力学特性与宏观行为模式之间关联的研究。此外，研究者基于各自的实验提出了不同的隆起和对流机理，这些机理均具有一定的局限性，甚至对颗粒运动过程的认识上存在分歧，在何种情况下何种机理起主导作用，仍需进一步探讨和验证。

图1 竖直振动床中颗粒物质的行为

1.2 竖直振动颗粒床中颗粒沿直管的爬升

图2 竖直振动颗粒床中颗粒沿直管的爬升

在竖直振动颗粒床中插入直管，颗粒将在管内发生涨落，并最终达到一个稳定的平衡高度，如图2所示。AKIYAMA和SHIMOMURA[31-32]最早注意到这一特性，并将之用于测量壁面的剪切应力。随后，陈伟中与魏荣爵[33]除利用这一特性对竖直振动床中颗粒的自放大行为进行研究外，还专门研究了颗粒在管内的爬升规律，并称颗粒沿直管的爬升为“类毛细现象”[34]。2009年，TATEMOTO等[35]利用DEM再现了管内外高度差的形成，获得了管径对颗粒爬升高度、颗粒对流特性的影响规律。与上述研究采用静止的开口直管不同，2013年，LIU等[36]对放置在颗粒床表面的、可以自由移动的顶端封闭管在颗粒床受到竖直振动时颗粒的行为进行实验研究，也发现了类似的颗粒爬升现象，并认为间隙气体是颗粒爬升的必要条件。

1.3 竖直振动U形管中颗粒的迁移

1976年，GUTMAN[37]首次提出U形管不稳定性，即在U形管两臂颗粒柱等高的情况下，对U形管施加竖直振动，颗粒将由一臂向另一臂迁移，从而两臂颗粒柱出现高度差的现象；并指出这种现象是由于 U形管底部气体压力梯度作用促使颗粒持续向颗粒柱较高的一侧迁移导致的，这种高度差形成机制被称为间隙气体作用机理。1991年，RAJCHENBACH[38]用对流机理对U形管不稳定性进行解释，认为颗粒从随机运动的高速区向低速区的迁移引起的对流导致了 U形管两臂颗粒柱高度差的产生。2009年，SÁNCHEZ等[39]对U形管不稳定性进行了系统的实验研究，考察了水平振动分量对颗粒柱高度差演变的影响，并基于循环流化机理建立了颗粒柱高度差演变动力学模型，循环流化机理认为一个振动周期内，颗粒膨胀阶段为流化阶段，此时颗粒流动，其余时间颗粒运动受阻。2010年，DARIAS等[3]实验研究了 U形管两臂颗粒柱高度差的演变随振动强度和频率的变化情况。2011年，PÉREZ和SÁNCHEZ等[40]通过在U形管内壁覆盖砂纸增大器壁与颗粒之间的摩擦系数，实验研究了摩擦系数对U形管两臂颗粒柱高度差增长率的影响，以验证循环流化机理[39]的可靠性，发现该模型在摩擦系数较低时和实验符合较好，但在摩擦系数较高时和实验有很大差异。2013年，DARIAS等[41]通过实验和二维DEM模拟分别得到竖直振动U形管两臂颗粒柱高度差的演变过程（图3），然而模拟中将球形颗粒按片状处理，使得数值模拟结果难以准确反映实验现象。2015年，SÁNCHEZ 等[42]利用改进的循环流化模型，研究了竖直振动U形管两臂颗粒柱高度差的影响因素，并提出延迟耦合的概念解释了大振动强度下高度差消失的现象，但模型的有效性缺少验证。此外，一些学者[43-45]研究了竖直振动分割容器中颗粒的不稳定性，这些研究可为竖直振动U形管中颗粒迁移的研究提供参考。综上所述，已有研究提出的竖直振动 U形管两臂颗粒柱高度差的产生机理有3种，即间隙气体作用、对流和循环流化，但各机理的作用强弱，需要通过更系统的研究来确定。另外，已有研究结果表明，振动强度和频率、水平振动分量、器壁与颗粒之间的摩擦系数等会对颗粒柱高度差的演变产生影响，但根据颗粒动力学，颗粒特性（如摩擦系数、粒径等）和U形管尺寸等也会对高度差演变带来影响，相应的影响规律仍有待探讨。总之，目前对竖直振动U形管两臂颗粒柱高度差的产生机理和影响因素的认识仍不充分，有必要结合已有实验结果，借助DEM 模拟的优势，开展更深入细致的数值模拟研究。

图3 实验得到的竖直振动U形管中颗粒的迁移过程[41]

1.4 静止颗粒床中颗粒沿竖直振动管的爬升

受竖直振动颗粒床中颗粒沿直管爬升[34-36]的启发，2013年，LIU等[46]率先针对颗粒床保持静止，而插入其中的直管发生振动时颗粒的行为模式进行实验研究，发现颗粒能够沿管迅速爬升并最终稳定在一定的高度，如图4所示。该方法为颗粒的逆重力输运提供了新途径。2014年，LIU 等[47]对振动管管口进行改进，实验研究了颗粒沿锥形口管的爬升，发现与采用直管相比，颗粒能够在更低的振动强度发生爬升；张富翁等[4]将颗粒床的竖直壁面视为周期性边界，基于 DEM模拟了一个振动周期内颗粒的受力状况，但是没有给出颗粒的爬升过程。2015年，LIU与ZHAO[48]根据文献[4，46]的实验结果建立了爬升高度随时间变化的半经验关系式，分析了颗粒爬升的“空穴填充”机理，并根据能量平衡关系推导出最大爬升高度的表达式。

图4 实验得到的静止颗粒床中颗粒沿竖直振动管的爬升[4]

2 竖直振动下颗粒物质行为模式的DEM模拟

鉴于竖直振动下颗粒的行为模式对化工过程的重要意义，而目前在此方面的研究，尤其是基于DEM 的数值模拟仍存在诸多不足，如竖直振动 U形管中颗粒迁移的DEM模拟仅见二维模拟，且采用的颗粒特性和实际颗粒差别很大[41]；对静止颗粒床中颗粒沿竖直振动管爬升的DEM模拟中，将颗粒床的固体壁面视为周期性边界，这与实际不符，并且模拟结果无法体现颗粒爬升的全过程[4]。因此，本节将针对竖直振动U形管中和插入静止颗粒床的竖直振动管中颗粒物质的行为模式分别开展三维DEM模拟。

2.1 数学模型

根据牛顿第二定律，颗粒系中任意颗粒i的运动方程如式(1)、式(2)。

式中，mi和Ii分别为颗粒i的质量和转动惯量；vi和ωi分别为颗粒i的速度和角速度；t为时间；g为重力加速度N为与颗粒i相接触的颗粒的个数；Fn,ij和 Ft,ij分别为颗粒i和与它相接触的颗粒j之间的法向接触力和切向接触力； Mt, ij为由于颗粒j对颗粒i的切向接触力产生的力矩；Mr,ij为由于颗粒j对颗粒i的滚动摩擦力产生的力矩。

根据黏弹性接触模型[49]和修正Cundall-Strack模型[50]，法向接触力和切向接触力如式(3)、式(4)。

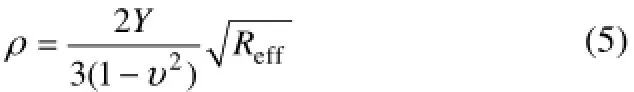
采用定向恒转矩模型（directional constant torque model）[53]，r,ijM 如式(6)。

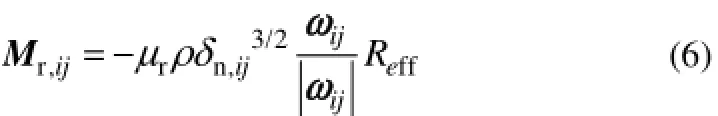
式中，μr为滚动摩擦系数；ijω为颗粒i和j的相对角速度。

对于颗粒与壁面的相互作用，将壁面视为粒径无限大的颗粒处理。利用上述模型，借助开源DEM模拟软件 LIGGGHTS[54]对竖直振动下颗粒的行为模式进行数值模拟。

2.2 竖直振动U形管中颗粒迁移的DEM模拟

数值模拟时采用与DARIAS等[41]的实验相同的参数条件，其中，杨氏模量、泊松比、恢复系数和摩擦系数并未给出，本文模拟中依据颗粒的型号从文献[55]、[56]中获得这些参数的数值，见表1。

表1 数值模拟参数

数值模拟结果如图5所示，对比图3给出的实验结果，可知二者吻合良好，并且通过数值模拟能够给出更为丰富的颗粒流动过程特性。

2.3 竖直振动管中颗粒爬升的DEM模拟

采用和张富翁等[4]的 DEM模拟相同的计算参数进行数值模拟。首先采用与文献[4]一致的边界条件，即将竖直壁面视为周期性边界，模拟结果显示：在最初的2个振动周期内管内颗粒柱高度出现明显涨落后，颗粒柱回到初始位置；之后颗粒柱几乎保持不变，这与实验不符。为解决这一问题，笔者采用切合实际的边界条件，即将所有壁面均视为有摩擦的固壁边界，得到了颗粒沿竖直振动管的爬升高度随时间的演变过程，如图6所示。可见，爬升高度先迅速增大，随后增速趋于平缓，最终稳定在一定的高度，与实验结果取得了一致。对比上述将竖直壁面视为周期性和有摩擦的固壁边界时的数值模拟结果可知，模拟中应采用有摩擦的固壁边界。

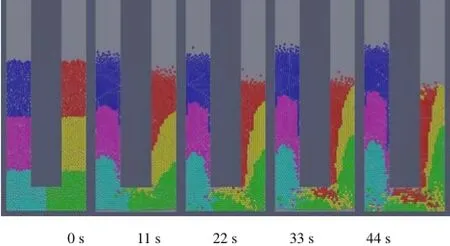
图5 DEM模拟得到的竖直振动U形管中颗粒的迁移过程

图6 DEM模拟得到的静止颗粒床中颗粒沿竖直振动管的爬升过程（T为振动周期）

3 结 语

竖直振动下颗粒物质表现出不同寻常的行为模式，如颗粒的隆起、对流、表面波和斑图，以及颗粒沿插入振动颗粒床的直管的爬升、在竖直振动U形管中的迁移、沿插入静止颗粒床的竖直振动管的爬升等。针对这些行为模式的研究已陆续开展，并成为热点，然而已有研究集中在通过实验探讨颗粒物质的宏观行为模式和影响因素，针对颗粒行为模式机理不同研究者提出不同的观点，缺乏对单个颗粒微观运动规律的研究，尚未建立颗粒微观运动规律与宏观行为模式的本质联系，使得在颗粒行为模式机理上无法形成共识。单纯依靠实验研究难以充分揭示颗粒的微观运动特性，阻碍了竖直振动下颗粒行为模式研究的发展。鉴于DEM模拟可以从颗粒尺度上考察相关量的变化，便于揭示颗粒行为模式的机理，作者针对竖直振动U形管和插入静止颗粒床的竖直振动管中颗粒物质的行为模式进行三维DEM模拟再现，为今后利用DEM深层次研究竖直振动下颗粒物质行为模式提供依据。在未来的研究中，一方面应充分发挥DEM在研究颗粒行为模式机理和颗粒输运过程优化上的优势，深入研究竖直振动下颗粒微观动力学和宏观行为模式的关联，将实验和DEM模拟结果相结合，构建能够定量反映颗粒行为的方程式；另一方面竖直振动管内颗粒的爬升能够提供一种全新的颗粒物质输运方式，且可实现颗粒物质在真空中的逆重力输运，具有重要的工程意义和研究价值，应对其爬升机理和影响因素做进一步研究。

参考文献

[1] 张立栋，李连好，程硕，等.颗粒在圆形偏心滚筒内的运动模式[J].化工进展，2015，34（9）：3244-3247.

[2] VAN GERNER H J，VAN DER HOEF M A，VAN DER MEER D，et al.Interplay of air and sand：faraday heaping unravelled[J].Physical Review E，2007，76（5）：051305.

[3] DARIAS J R，SÁNCHEZ I，GUTIÉRREZ G.Experimental study on the vertical motion of grains in a vibrated U-tube[J].Granular Matter，2010，13（1）：13-17.

[4] 张富翁，王立，刘传平，等.竖直振动管中颗粒的上升运动[J].物理学报，2014，63（1）：014501.

[5] ESHUIS P，VAN DER WEELE K，VAN Der MEER D，et al.Phase diagram of vertically shaken granular matter[J].Physics of Fluids，2007，19（12）：123301.

[6] RAPAPORT D C.Subharmonic surface waves in vibrated granular media[J].Physica A：Statistical Mechanics and its Applications，1998，249（1）：232-238.

[7] PAK H K，BEHRINGER R P.Surface waves in vertically vibrated granular materials[J].Physical Review Letters，1993，71（12）：1832-1837.

[8] FARADAY M.On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces[J].Philosophical Transactions of the Royal Society of London，1831，121：299-340.

[9] MELO F，UMBANHOWAR P，SWINNEY H L.Transition to parametric wave patterns in a vertically oscillated granular layer[J].Physical Review Letters，1994，72（1）：172-176.

[10] UMBANHOWAR P B，MELO F，SWINNEY H L.Localized excitations in a vertically vibrated granular layer[J].Nature，1996，382（6594）：793-796.

[11] 陈伟中.颗粒物质表面孤立子波形隆起与内部对流[J].物理学报，1995，44（3）：427-431.

[12] AOKI K M，AKIYAMA T，MAKI Y，et al.Convective roll patterns in vertically vibrated beds of granules[J].Physical Review E，1996，54（1）：874-883.

[13] JAEGER H M，NAGEL S R，Behringer R P.The physics of granular materials[J].Physics Today，1996，49（4）：32-38.

[14] CERDA E，MELO F，RICA S.Model for subharmonic waves in granular materials[J].Physical Review Letters，1997，79（23）：4570-4573.

[15] CHEN W Z，WEI R J，WANG B R.Formation mechanism of the soliton-shape heap and convection in granular materials under vibration[J].Physics Letters A，1997，228（4）：321-328.

[16] LEE J.Mechanism for surface waves in vibrated granular material[J].Europhysics Letters，1999，47（4）：515-521.

[17] SUI L，MIAO G Q，WEI R J.Surface instability of a vertically oscillating granular layer[J].Chinese Physics Letters，2001，18（4）：614-615.

[18] WI H S，KIM K，PAK H K.Pattern selection on granular layers under multiple frequency forcing[J].Journal Korean Physical Society，2001，38（5）：573-576.

[19] WONG Y S，GAN C H，WANG C H.Study on granular dynamics in vertically vibrated beds using tracking technique[EB/OL].[2015-10-13].http://dspace.mit.edu/handle/1721.1/7495.

[20] 孔维姝，胡林，李世雄，等.探讨激振频率和容器宽度对颗粒层中对流的影响[J].振动与冲击，2010，29（4）：88-91.

[21] 李芳芳，薛琨，白春华.竖直振动颗粒床对流机制的颗粒尺度实验研究[J].实验力学，2013，28（3）290-298.

[22] YAMADA T M，KATSURAGI H.Scaling of convective velocity in a vertically vibrated granular bed[J].Planetary and Space Science，2014，100（2）：79-86.

[23] ZHANG F，WANG L，LIU C，et al.Patterns of convective flow in a vertically vibrated granular bed[J].Physics Letters A，2014，378（18）：1303-1308.

[24] NOWAK E R，KNIGHT J B，BEN-Naim E，et al.Density fluctuations in vibrated granular materials[J].Physical Review E，1998，57(2): 1971-1982.

[25] 刘传平，王立，张富翁.垂直振动床中的能量传递与耗散[J].物理学报，2014，63（4）：044502.

[26] 彭政，蒋亦民，刘锐，等.垂直振动激发下颗粒物质的能量耗散[J].物理学报，2013，62（2）：024502.

[27] 韩红，姜泽辉，李翛然，等.器壁滑动摩擦力对受振颗粒体系中冲击力倍周期分岔过程的影响[J].物理学报，2013，62（11）：114501.

[28] 姜泽辉，王运鹰，吴晶.窄振动颗粒床中的运动模式[J].物理学报，2006，55（9）：4748-4753.

[29] JIANG Z H，WANG Y Y，WU J.Subharmonic motion of granular particles under vertical vibrations[J].Europhysics Letters，2006，74 （3）：417-423.

[30] JAEGER H M，NAGEL S R，BEHRINGER R P.Granular solids，liquids，and gases[J].Reviews of Modern Physics，1996，68（4）：1259-1273.

[31] AKIYAMA T，SHIMOMURA T.Measurements of wall shear stress in particle beds when vibrations are imposed vertically along the direction of shear[J].Advanced Powder Technology，1993，4（2）：129-142.

[32] AKIYAMA T，SHIMOMURA T.Investigation of wall shear stress in vibrating particle beds[J].Powder Technology，1991，66（3）：243-247.

[33] 陈伟中，魏荣爵.振动激励下的颗粒物质的有效隆起力[J].声学技术，1997，16（30）：149-151.

[34] CHEN W Z，WEI R J.A capillarity-like phenomenon in granular material under vertical vibration[J].Physics Letters A，1998，244（5）：389-393.

[35] TATEMOTO Y，NIWA Y，TAKESHITA T.Circulation of particles in a vibrated bed with an inner tube[J].Powder Technology，2009，192 （3）：279-286.

[36] LIU C P，WU P，ZHANG F W，et al.Particle climbing induced by reciprocating air flow[J].Applied Physics Letters，2013，102（18）：183507.

[37] GUTMAN R G.Vibrated beds of powders part I: a theoretical model for the vibrated bed[J].Chemical Engineers Research and Design，1976，54a：174-183.

[38] RAJCHENBACH J.Dilatant process for convective motion in a sand heap[J].Europhysics Letters，1991，16（2）：149-152.

[39] SÁNCHEZ I，DARIAS J R，PAREDES R，et al.Vertical granular transport in a vibrated U-tube[C]// Appert-Rolland C，Chevoir F，Gondret P， et al.Traffic and Granular Flowʹ07.Berlin: Springer-Verlag Berlin.2009：545-554.

[40] PÉREZ B，SÁNCHEZ I.Effect of friction on the granular U-tube instability[J].Mechanics Research Communications，2011，38（3）：244-248.

[41] DARIAS J，SÁNCHEZ I，GUTIÉRREZ G，et al.Study of the accumulation of grains in a two dimensional vibrated U-tube without interstitial fluid[J].Advanced Powder Technology，2013，24（6）：1095-1099.

[42] SÁNCHEZ I，DÍAZ A A，GUERRERO B，et al.Improved model for the U-tube granular instability：analytical solution and delayed coupling[J].Mechanics Research Communications，2015，67：1-7.

[43] CLEMENT C P，PACHECO-MARTINEZ H A，Swift M R，et al.Partition instability in water-immersed granular systems[J].Physical Review E，2009，80（1）：011311.

[44] KING P J，LOPEZ-ALCARAZ P，PACHECO-MARTINEZ H A，et al.Instabilities in vertically vibrated fluid-grain systems[J].The European Physical Journal E，2007，22（3）：219-226.

[45] OHTSUKI T，KINOSHITA D，NAKADA Y，et al.Surface level migration in vibrating beds of cohesionless granular materials[J].Physical Review E，1998，58（6）：7650-7656.

[46] LIU C P，WU P，WANG L.Particle climbing along a vibrating tube: a vibrating tube that acts as a pump for lifting granular materials from a silo[J].Soft Matter，2013，9（19）：4762-4766.

[47] LIU C P，ZHANG F W，WU P，et al.Effect of hoisting tube shape on particle climbing[J].Powder Technology，2014，259：137-143.

[48] LIU Y，ZHAO J H.Experimental study and analysis on the rising motion of grains in a vertically-vibrated pipe[J].Chinese Physics B，2015，24（3）：034502.

[49] BRILLIANTOV N V，SPAHN F，HERTZSCH J-M，et al.Model for collisions in granular gases[J].Physical Review E，1996，53(5): 5382-5392.

[50] CUNDALL P A，STRACK O D.A discrete numerical model for granular assemblies[J].Geotechnique，1979，29（1）：47-65.

[51] MÜLLER P，PÖSCHEL T.Collision of viscoelastic spheres: Compact expressions for the coefficient of normal restitution[J].Physical Review E，2011，84（2）：021302.

[52] RYCROFT C H，ORPE A V，KUDROLLI A.Physical test of a particle simulation model in a sheared granular system[J].Physical Review E，2009，80（3）：031305.

[53] AI J，CHEN J F，ROTTER J M，et al.Assessment of rolling resistance models in discrete element simulations[J].Powder Technology，2011，206（3）：269-282.

[54] KLOSS C，GONIVA C，HAGER A，et al.Models，algorithms and validation for opensource DEM and CFD-DEM[J].Progress in Computational Fluid Dynamics，an International Journal，2012，12 （2）：140-152.

[55] GONDRET P，LANCE M，PETIT L.Bouncing motion of spherical particles in fluids[J].Physics of Fluids，2002，14（2）：643-652.

[56] JOSEPH G，ZENIT R，HUNT M，et al.Particle–wall collisions in a viscous fluid[J].Journal of Fluid Mechanics，2001，433：329-346.

第一作者：刘举（1988—），男，硕士研究生。联系人：凡凤仙，副教授，硕士生导师。E-mail fanfengxian@hotmail.com。

中图分类号：TQ 022.3

文献标志码：A

文章编号：1000-6613（2016）07-1956-07

DOI：10.16085/j.issn.1000-6613.2016.07.003

收稿日期：2015-10-20；修改稿日期：2016-01-26。

基金项目：国家自然科学基金（51206113，51176128）及上海市科委科研计划（13DZ2260900）项目。

Research progress on behavior mode of granular matter under vertical vibration

LIU Ju1,2，BAI Pengbo1,2，FAN Fengxian1,2，HU Xiaohong1,2
（1School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China；2Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China）

Abstract：Research on behavior mode of granular matter under vertical vibration is of great significance in improving the efficiencies of chemical engineering industries.The research has been a popular topic and continuous progresses have been made in this field.The behavior modes of granular matter under vibration were summarized as granular behaviors in a vertically vibrated bed，particle climbing along the pipe inserted in the vertically vibrated granular bed，particle migration in the vibrated U-tube and particle climbing along the vertically vibrated pipe inserted in the static granular bed，and the relevant research progresses were reviewed.It was found that the motion of granular matter was still not well understood and that the mechanism lying in the granular behavior mode remained controversial.Since the discrete element method (DEM) can be used to obtain the information of individual particle motion and thus to well reflect the mechanism and behavior of granular process，the DEM simulations on behavior modes of granular matter both in a vertically vibrated U-tube and in a vertically vibrated pipe were performed to reproduce the experimental results.On this basis，it was proposed that taking advantage of the DEM，the future work should focus on the investigation of the dynamic nature of granular behavior mode and the factors affecting the granular behavior mode in order to provide theoretical foundation and method guidance for the optimization of granular transportation process.

Key words:vertical vibration；granular matter；behavior mode；discrete element method (DEM)