径向动压浮环轴承-转子系统多稳定区域研究

郭　红， 张直明， 张绍林， 岑少起

(1. 郑州大学 机械工程学院，郑州　450001； 2. 上海大学 机电工程与自动化学院，上海　200072)



径向动压浮环轴承-转子系统多稳定区域研究

郭红1， 张直明2， 张绍林1， 岑少起1

(1. 郑州大学 机械工程学院，郑州450001； 2. 上海大学 机电工程与自动化学院，上海200072)

摘要：以径向动压浮环轴承为研究对象，针对轴颈、浮环建立统一的动力学方程，用Routh-Hurwitz准则给出单质量刚性对称浮环轴承-转子系统稳定性判据。用有限差分计算某高速径向动压浮环轴承刚度、阻尼系数，获得不同工况下系统稳定性曲线。结果表明，小偏心率下系统升速过程中呈现多个稳定区域，且随偏心率、内外膜半径间隙变化而变化。油膜温度变化亦会影响系统稳定性。为高速浮环轴承稳定性整体建模、分析提供借鉴。

关键词：径向浮环轴承；刚度；阻尼；失稳转速；稳定区域

浮环轴承有内外两层油膜，具有稳定性好、失稳界限转速高等优点，广泛用于涡轮机、透平机等高速旋转机械。对不同结构滑动轴承特性及应用已有诸多研究[1-3]，如郭红等[4-5]建立内外膜层油膜数学模型，利用有限元计算获得不同工况的静、动态特性，并推导出浮环轴承的稳定性判断准则；Tian等[6-8]探讨非线性因素对透平机浮环轴承特性影响；Amamou等[9]在非线性领域对浮环轴承-转子系统稳定性进行分析；Andres等[10]考虑温度对浮环轴承性能影响；郭增林等[11]在合理简化基础上研究滑动轴承转子系统多稳定区形态。

本文以动压浮环轴承支承单质量刚性对称转子为研究对象，建立轴颈、浮环动力学方程，利用有限差分法获得不同工况下系统稳定性曲线，并分析内外膜间隙、偏心率及温度对多稳定区域影响。

1径向动压浮环轴承控制方程

图1为某径向动压浮环轴承内外膜结构展开示意图。在轴瓦内壁开设进油槽对外膜供油，浮环中央均匀开设6个进油孔对内膜供油。

图1　浮环轴承内外膜结构Fig.1 Inner and outer film structure of floating ring bearing

1.1控制方程

(1)

1.2边界条件

图2　压力边界条件Fig.2 Pressure boundary condition

压力边界条件为

(2)

式中：Γ1为轴承端面；Γ2为进油边。

1.3特性参数及浮环平衡工作条件

对内外膜控制方程进行有限差分法离散，迭代得该动压浮环轴承内外膜各静态特性参数。内、外膜承载力分别为

(3)

内膜作用于轴颈、浮环及外膜作用于浮环的摩擦力分别为

(4)

内、外膜作用于浮环的摩擦力矩为

Mf12=Ff12r1,Mf2=Ff2r2

(5)

内、外膜摩擦功耗为

Hf1=Ff1r1(Ω1-Ω2),Hf2=Ff2r2Ω2

(6)

内、外膜流量为

(7)

内、外膜温升为

(8)

内外膜作用于浮环的力、力矩相等时浮环即可保持平衡运转。计算时通过调整环速比及内膜偏心率保证浮环平衡，即

Fr1=Fr2,Mf12=Mf2

(9)

在静特性参数计算基础上获得内、外膜刚度、阻尼系数分别为

(10)

式中:di为轴承直径(mm)；li为轴承长度(mm)；hi为油膜厚度(mm)；ci为油膜间隙(mm)；Ω1为轴颈角速度(1/s)；Ω2为浮环角速度(1/s)；ei为偏心距(mm)；θi为偏位角；μ为油黏度(Pa·s)；ρ为油密度(kg/m3)；cv为油比热(J/(kg·℃))；pi为油膜压力(Pa)；pini为进油压力(MPa)；m1为转子质量(kg)；m2为浮环质量(kg)；Fri为承载力(N)；Ffi为摩擦力(N)；Mfi为摩擦力矩(N·mm)；Hfi为摩擦功耗(N·mm/s)；Qi为流量(mm3/s)；ΔTi为温升(℃)；kmni(m,n=x,y) 为刚度(N/mm)；bmni(m,n=x,y)为阻尼(N·s/mm)。下标i=1表示内膜参数，i=2表示外膜参数；有上划线者为无量纲参数，其余为有量纲参数。其它未标注者同一般润滑理论规范。

2动压向心浮环轴承稳定性分析

浮环轴承-转子模型见图3。采用单质量刚性对称转子系统，设轴颈质量2m1，浮环质量2m2。内层油膜动力特性系数为kxx1,kxy1,kyx1,kyy1，bxx1,bxy1,byx1,byy1；外层油膜动力特性系数为kxx2,kxy2,kyx2,kyy2，bxx2,bxy2,byx2,byy2。作用于轴颈的简谐变动力为Fx,Fy；轴颈简谐变动位移x1,y1；浮环简谐变动位移x2,y2。考虑浮环质量较转子小，为简化计算建模时忽略浮环质量m2。

图3　浮环轴承内外膜动力学模型Fig.3 Dynamics model of floating ring bearing

轴颈运动方程为

(11)

浮环运动方程为

引入各无量纲因子利用Routh-Hurwitz准则，可得该系统存在非平凡解的特征方程(见文献[5])为

(13)

该动压浮环轴承-转子系统稳定性判别条件为

(14)

式中：

M1(Bxx1Byy1-Bxy1Byx1)(Bxx2+Byy2)

M1(Bxx2Byy2-Bxy2Byx2)(Kxx1+Kyy1)+

M1[(Bxx2+Byy2)G1+(Bxx1+Byy1)G2]+

(Bxx1Byy1-Bxy1Byx1)(Bxx2Byy2-Bxy2Byx2)

M1+(Bxx1+Byy1)(Kxx2Kyy2-Kxy2Kyx2)+

M1[(Bxx2+Byy2)(Kxx1Kyy1-Kxy1Kyx1)]+

(Bxx1Byy1-Bxy1Byx1)G2+(Bxx2Byy2-Bxy2Byx2)G1

M1(Kxx1+Kyy1)(Kxx2Kyy2-Kxy2Kyx2)+

(Bxx1Byy1-Bxy1Byx1)(Kxx2Kyy2-Kxy2Kyx2)+

(Bxx2Byy2-Bxy2Byx2)(Kxx1Kyy1-Kxy1Kyx1)+G1G2

(Kxx1Kyy1-Kxy1Kyx1)G2

Ks=(Kxx1+Kxx2)(Kyy1+Kyy2)-

(Kxy1+Kxy2)(Kyx1+Kyx2)

Bs=(Bxx1+Bxx2)(Byy1+Byy2)-

(Bxy1+Bxy2)(Byx1+Byx2)

G1=Bxx1Kyy1+Byy1Kxx1-Bxy1Kyx1-Byx1Kxy1

G2=Bxx2Kyy2+Byy2Kxx2-Bxy2Kyx2-Byx2Kxy2

Gs=(Bxx1+Bxx2)(Kyy1+Kyy2)+(Byy1+Byy2)(Kxx1+Kxx2)-

(Bxy1+Bxy2)(Kyx1+Kyx2)-(Byx1+Byx2)(Kxy1+Kxy2)

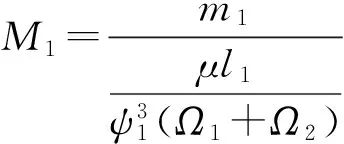
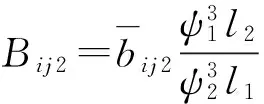
3向心浮环轴承稳定性分析算例

设图1的向心浮环动压轴承结构参数为:内膜直径21 mm，轴向宽度16.8 mm；外膜直径32 mm，轴向宽度20 mm；取润滑油黏度0.032 Pa·s(50 ℃)，密度850～899 kg/m3，供油压力0.4 MPa，比热1 800[J/(kg·℃)]，转子质量2.48 kg。计算时给定外膜偏心率，在一定主轴转速下通过迭代保证浮环平衡。由式(8)，浮环平衡运转时内外膜平均温升随转速及偏心率变化曲线见图4、图5。由2图可见，该浮环轴承内外膜温升随转速增加迅速上升，因此计算分析时分别取3种油膜平均温度50 ℃、80 ℃、100 ℃，计算静动态特性参数，再按式(14)判断系统的稳定性。

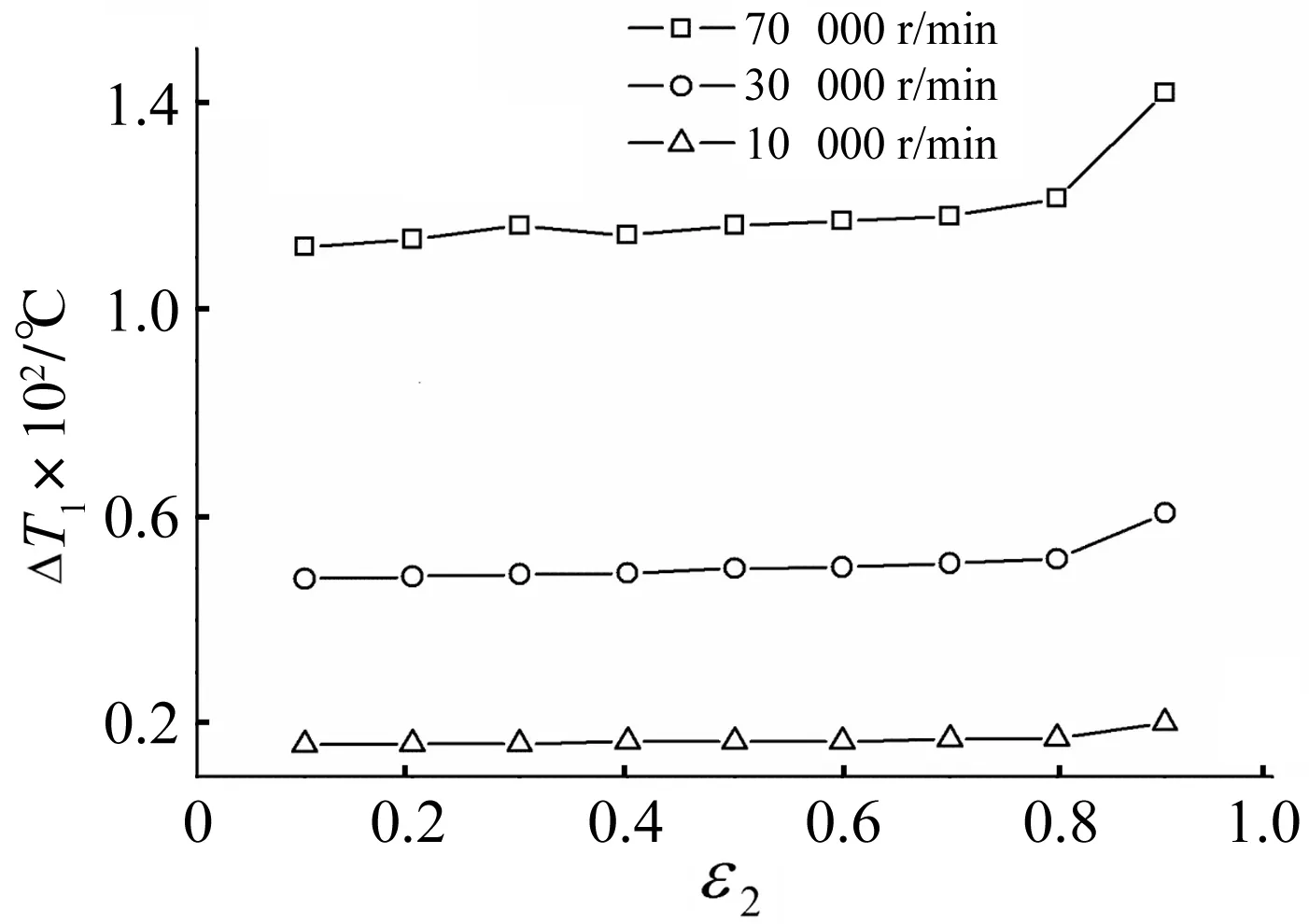
图4　内膜温升Fig.4 Temperature rise of inner film

图5　外膜温升Fig.5 Temperature rise of outer film

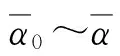
只有D5会有正负改变，因此可按D5符号判断系统的稳定性。系统运转于小偏心率时，在升速过程中会出现多个稳定区域，而大偏心率时不存在多稳定区域。

3.1内外膜半径间隙对稳定区域的影响

图6为内膜间隙c1=0.02 mm、外膜间隙c2= 0.052 mm时3种偏心率下稳定性曲线。由图6看出，各偏心率下随着转速的提高，系统均由稳定运转转变为不稳定，但大偏心率下失稳转速高于小偏心率；相同转速下系统运转在大偏心率下稳定性优于小偏心率。该组参数下浮环动压轴承稳定性曲线失稳前波动较小，D5接近零。图7为内膜间隙c1=0.03 mm，外膜间隙c2=0.052 mm时3种偏心率下稳定性曲线。由图7看出，随转速提高系统由稳定运转变为不稳定，升速过程中稳定性曲线出现波动，波幅较图6大，但D5变化幅度未超±10。图8为内膜间隙c1=0.035 mm，外膜间隙c2=0.052 mm时3种偏心率下的稳定性曲线。由图8看出，升速过程中稳定性曲线出现波动，且D5变化幅度较大。

图6 稳定性参数D5Fig.6StabilityparametersD5图7 稳定性参数D5Fig.7StabilityparametersD5图8 稳定性参数D5Fig.8StabilityparametersD5

为进一步定量说明半径间隙对稳定性影响，取外膜偏心率ε2=0.15及半径间隙c2=0.052 mm，不同内膜半径间隙下稳定性曲线见图9～图11。图9为c1=0.02 mm时升速过程稳定性曲线，存在1个界限速度点P1，对应失稳速度为7.4×105r/min。图10为c1=0.03 mm时升速过程稳定性曲线，存在3个界限速度点P1～P3，对应失稳转速分别为3.2×105r/min、9.7×105r/min及13.5×105r/min。图11为c1=0.035 mm时升速过程稳定性曲线，存在3个界限速度点P1～P3，对应失稳转速分别为2.1×105r/min、11.1×105r/min及18.6×105r/min。由此看出，相同偏心率下外膜间隙不变时内膜间隙越小，升速过程中稳定区域变动越小，但最终失稳转速低。反之，内膜间隙越大稳定区域波动越厉害，但最终失稳转速高。因此需据设计要求选择合理的油膜间隙，在满足工作转速要求下避免过大波动。就本例而言，图10的参数更合适。

3.2油膜温度对稳定性曲线影响

轴承结构参数同前，取内膜间隙c1=0.03 mm，外膜间隙c2=0.052 mm，3种偏心率下不同油膜温度时稳定性曲线分别见图12～图14。图12为外膜偏心率ε2=0.1时3种温度的稳定曲线，可见，50℃时最终失稳转速为22.7×105r/min，80℃时为16.7×105r/min，100℃时为8.9×105r/min，失稳转速随温度上升迅速下降。图13外膜偏心率ε2=0.2、图14外膜偏心率ε2=0.3时亦有相同规律。偏心率越大稳定性波动幅度受温度影响越大。设计动压浮环轴承时，应警惕油膜温度升高引起的失稳转速降低。

图9 稳定性参数D5(ε2=0.15)Fig.9StabilityparametersD5图10 稳定性参数D5(ε2=0.15)Fig.10StabilityparametersD5图11 稳定性参数D5(ε2=0.15)Fig.11StabilityparametersD5

图12 温度对稳定性影响(ε2=0.1)Fig.12Influenceoftemperatureonstability图13 温度对稳定性影响(ε2=0.2)Fig.13Influenceoftemperatureonstability图14 温度对稳定性影响(ε2=0.3)Fig.14Influenceoftemperatureonstability

4结论

(1) 考虑浮环轴承内外两层油膜相互作用，建立动压浮环轴承转子系统动力学方程，并给出径向动压浮环动静压轴承稳定性判据。

(2) 小偏心时存在多稳定区域，在外膜间隙不变情况下，内膜间隙越小失稳区域变动越小，但最终失稳转速低。反之，内膜间隙越大稳定速度波动越厉害，但最终失稳转速高。

(3) 系统稳定性随温度改变而改变，偏心率越大受温度影响越明显；相同偏心率下，系统稳定性随油膜温度升高而下降。

参 考 文 献

[1] 万召, 孟光, 荆建平, 等. 燃气轮机转子-轴承系统的油膜涡动分析[J]. 振动与冲击, 2011, 30(3): 38-41.

WAN Zhao, MENG Guang, JING Jian-ping, et al. Analysis on oil whirl of gas turbine rotor-bearing system[J]. Journal of Vibration and Shock, 2011, 30(3): 38-41.

[2] 杨金福,杨昆, 付忠广, 等. 转子滑动轴承系统中油膜谐波振荡过程的试验研究[J]. 燃气涡轮试验与研究, 2007, 20(3): 42-47.

YANG Jin-fu, YANG Kun, FU Zhong-guang, et al. Experimental rearch on the harmonic oil whip in sliding bearing-rotor system[J]. Gas Turbine Experiment and Research, 2007, 20(3): 42-47.

[3] Chen W J. Rotordynamics and bearing design of turbochargers[J]. Mechanical Systems and Signal Processing, 2012,29:77-89.

[4] Guo H, Lai X M, Wu X L, et al. Performance of flat capillary compensated deep/shallow pockets hydrostatic/ hydrodynamic journal-thrust floating ring bearing[J]. Tribology Transcations, 2009, 52(2): 204-212.

[5] 郭红,张直明,岑少起,等. 径向浮环动静压轴承稳定性研究[J]. 振动与冲击, 2012,31(17): 17-21.

GUO Hong, ZHANG Zhi-ming, CEN Shao-qi, et al. Stability of journal floating ring hybrid bearing[J]. Journal of Vibration and Shock, 2012, 31(17): 17-21.

[6] Tian L,Wang W J, Peng Z J. Nonlinear effects of unbalance in the rotor-floating ring bearing system of turbochargers [J]. Mechanical Systems and Signal Processing, 2013,34: 298-320.

[7] Tian L,Wang W J, Peng Z J. Dynamic behaviours of a full floating ring bearing supported turbocharger rotor with engine excitation[J].Journal of Sound and Vibration, 2011, 330:4851-4874.

[8] Tian L,Wang W J, Peng Z J. Effects of bearing outer clearance on the dynamic behaviours of the full floating ring bearing supported turbocharge rotor[J]. Mechanical System and Signal Processing, 2012, 31:155-175.

[9] Amamou A, Chouchane M.Non-linear stability analysis of floating ring bearings using Hopf bifurcation theory[J]. Journal of Mechanical Engineering Science,2011,225(12): 2804-2818.

[10] Andrés L S, Barbarie V, Bhattacharya A,et al. On the effect of thermal energy transport to the performance of (semi) floating ring bearing systems for automotive turbochargers [J].Journal of Engineering for Gas Turbines and Power, 2012, 134(10): 561-570.

[11] 郭增林,杨益华. 滑动轴承转子系统多稳定区形态特性研究[J]. 机械强度, 2001, 23(2): 138-140.

GUO Zeng-lin, YANG Yi-hua. Study on pattern characteristics of multi stable regions of hydrodynamic bearing-rotor system[J]. Journal of Mechanical Strength, 2001, 23(2): 138-140.

基金项目：国家自然科学基金资助项目(51075373)

收稿日期：2014-08-19修改稿收到日期：2014-12-26

中图分类号:TH133.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.028

Multi stable regions of hydrodynamic floating ring journal bearing-rotor system

GUO Hong1, ZHANG Zhi-ming2, ZHANG Shao-lin1, CEN Shao-qi1

(1. School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001, China; 2. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200072, China)

Abstract:A unitized dynamics model for the journal and floating ring of a hydrodynamic floating ring journal bearing was established. The stability criterion of the floating ring journal bearing was obtained using the Routh-Hurwitz method. The stiffnesses and damping coefficients under different operation conditons of the hydrodynamic floating ring journal bearing were calculated with the finite difference method. On this base, the judgment factors of stability criterion were acquired. The results show that floating ring bearing has multi stable regions under small eccentricity of the rotor. At the same time, stable regions change with the eccentricity, radial clearance and lubricant temperature. The results are of referential value in the model integrality and stability analysis of floating ring hybrid journal bearing.

Key words:floating ring journal bearing; threshold speed; multi stable regions

第一作者 郭红 女，博士，教授，1970年9月生

邮箱: gghhletter@zzu.edu.cn