含摩擦与间隙的失谐叶盘系统振动局部化研究
曾海楠, 曹树谦, 苏永雷
(1.天津大学 机械工程学院,天津 300072; 2.天津市非线性动力学与混沌控制重点实验室, 天津 300072;3.长安汽车工程研究总院 CAE工程所,重庆 401120)
含摩擦与间隙的失谐叶盘系统振动局部化研究
曾海楠1,2, 曹树谦1,2, 苏永雷3
(1.天津大学 机械工程学院,天津300072; 2.天津市非线性动力学与混沌控制重点实验室, 天津300072;3.长安汽车工程研究总院 CAE工程所,重庆401120)
摘要:针对叶片榫头与轮盘榫槽连接处间隙及摩擦,基于叶盘结构典型集中参数模型,建立含干摩擦、间隙的非线性动力学方程,研究失谐叶盘系统振动局部化。在叶身刚度随机失谐下分析叶盘系统对不同耦合刚度的固有特性及共振响应。结果表明,非线性谐调叶盘系统亦出现振动局部化现象。利用振幅放大系数对线性、非线性失谐叶盘系统振动响应局部化研究,振幅放大系数呈失谐阈值现象,且非线性干摩擦、间隙作用会降低失谐系统振动响应局部化程度。而谐调叶盘系统非线性振动研究表明,随气流激励力频率变化,系统呈非简谐单周期运动、多周期谐波运动、混沌运动等多种动力学行为。失谐因素存在会使非线性失谐叶盘系统动力学行为更复杂。
关键词:叶盘系统;失谐;振动局部化;干摩擦;间隙;振幅放大系数;非线性动力学
叶盘系统为航空涡轮发动机转子基本组件,发动机运行安全可靠性主要依赖于旋转部件结构完整性。通常,叶盘系统被设计成谐调的,呈循环对称周期结构。而因制造误差、运转使用中磨损等原因会使叶片特性有小量差别,即失谐。失谐会使系统振动响应局限在较小叶片区域,导致该区域振动响应远大于其它部位,即振动局部化现象[1-5]。振动能量空间局部化使少数叶片应力显著增加,导致叶片过早发生疲劳损伤[6]。王建军等[7]提出基于叶片振型位移、模态应力及应变能3种定量描述失谐叶盘结构模态局部化方法。王培屹等[8]利用振幅放大系数对失谐叶盘系统振动响应局部化程度进行定量描述。Choi等[9-10]研究认为振幅放大系数随失谐强度增大到一定值后又随失谐强度进一步增大而减小,即存在一定失谐阈值。
采用非整体叶盘结构的现代航空发动机压气机工作叶片主要由叶身与榫头两部分组成。叶身与轮盘的连接为榫头等方式。榫头与轮盘榫槽之间含一定间隙,使榫头与轮盘连接处受热后自由膨胀减少热应力[11]。文献[4]用摄动法分析的各种系统参数条件下具有干摩擦散乱失谐的叶盘系统振动响应局部化问题未考虑榫头处间隙作用。Cigeroglu等[12]对含干摩擦阻尼器的非线性失谐叶盘系统进行振动分析,但亦未考虑间隙的存在。Sinclair等[13-15]认为榫头与榫槽之间含间隙,系统非线性因素源于榫头因变形扩张产生的接触力及接触面摩擦力,并利用线性弹簧模拟叶片根部弹性力。而因间隙存在,等效的弹性力为非线性的。Petrov[16]对3种含非线性界面(摩擦阻尼、间隙、三次非性弹簧)模型进行数值计算,但仍未考虑失谐因素。张亮等[17]采用集中参数模型分析榫头处干摩擦对失谐叶盘系统振动特性影响时,发现增加榫头摩擦能降低失谐叶盘系统振动局部化程度。王艾伦等[18-19]利用增量谐波平衡法研究含非线性摩擦力失谐叶盘系统振动响应,发现含非线性摩擦阻尼的谐调叶盘系统同样产生振动能量局部化现象,干摩擦失谐的不同形式对谐调叶盘系统振动局部化影响不同。现有文献虽对含非线性摩擦的失谐叶盘系统响应研究有一定成果,但对同时含非线性干摩擦力及间隙的失谐叶盘振动局部化研究较少。
本文以航空发动机压气机部分叶盘系统为研究背景,利用典型叶盘集中参数模型首次同时考虑干摩擦、间隙下利用四阶Runge-Kutta法对失谐叶盘系统非线性动力学方程进行数值求解,分析失谐叶盘系统非线性动力学行为。
1系统集中参数模型及动力学方程
1.1典型叶盘集中参数模型
压气机工作叶片主要由叶身、榫头两部分组成,轮盘边缘有榫槽。工作叶片通过榫头与轮盘连接。叶盘结构见图1。本文对叶盘结构建立集中参数模型,所用典型单扇区二自由度集中参数模型见图2。

图1 航空发动机低压压气机多级叶盘结构Fig.1 The structure of low pressure compressor multi-stage bladed disk of aero-engine
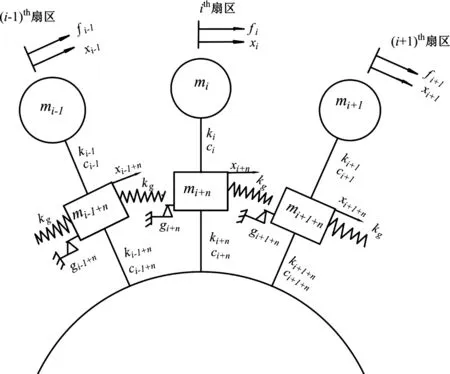
图2 叶盘集中参数模型Fig.2Lumped parameter model of a bladed disk
将轮盘等效为无质量的弹性体,不考虑轮盘动力学特性,只考虑榫槽对榫头摩擦、弹性约束作用。对原结构图中第i个叶片进行简化(对应第i个扇区),将叶身等效为质点,用图2集中质量块mi表示;将榫头等效为质点,用集中质量块mi+n表示。图1中叶身发生切向弯曲变形时与榫头之间产生弹性力,将其作用简化为图2中弯曲刚度为ki的无质量弹性杆。图1中单个榫头发生切向弯曲变形时轮盘榫槽亦会对单个榫头有弹性约束力,将此作用简化为图2中弯曲刚度为ki+n的无质量弹性杆。此弹性杆将榫头集中质量块与基础相连(图2中弧线),代表轮盘榫槽对对应单个扇区内榫头的弹性约束力。本文认为图1的榫头、榫槽为小间隙配合,当相邻榫头发生振动时轮盘对相邻榫头的耦合作用是变化的。对相邻扇区之间复杂的耦合作用力,用图2中耦合刚度为kg的分段线性弹簧连接相邻扇区,示意间隙的存在导致耦合作用力变化。ci,ci+n为第i个扇区叶身、榫头的等效阻尼;xi,xi+n为第i个扇区叶身、榫头位移沿轮盘切线方向;fi为作用于叶身的气流激振力,也沿轮盘切线方向。用榫头对轮盘榫槽(图2中固定端)的摩擦件模拟接触面的摩擦。gi+n为作用在第i个扇区榫头与轮盘榫槽连接位置的干摩擦力。
1.2含间隙的叶盘结构中耦合作用力
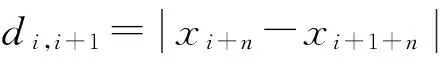
设第i扇区的等效榫头质量块受右侧扇区间作用力fkr及左侧扇区间作用力fkl,则由对耦合作用力分析可知
(1)
(2)
1.3干摩擦力
Wei等[21]分析干摩擦阻尼对近似循环结构局部化振动影响时用库仑干摩擦模型模拟摩擦阻尼。对具有缘板下阻尼件的叶盘系统分析时用叶片对地(轮盘)的摩擦件模拟摩擦阻尼。Berthillier等[22]对含摩擦阻尼器的叶盘系统进行振动响应分析采用库仑干摩擦模拟摩擦阻尼。本文模型的干摩擦亦用库仑摩擦模型,即
(3)
式中:μ为摩擦系数;Ni+n为第i扇区擦面间法向压力。
1.4气流激振力
作用于叶盘系统的外部激振力主要为气流激振力,通常简化为以圆周变化运动的周期激振源。此处采用谐和力形式为
fi=f0cos(ωt+φi)
(4)
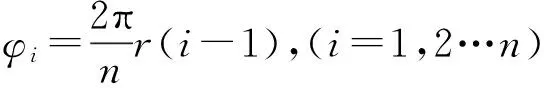
1.5系统动力学方程建立
由第i扇区叶身、榫头质量块受力分析,获得动力学方程为
(5)
将方程(5)写成矩阵形式,可得整体谐调叶盘系统非线性振动响应的力学模型,即
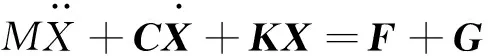
(6)
式中:M,C,K为系统质量、阻尼及刚度矩阵;X为位移矢量;F为作用于叶盘系统的气流激振力矢量;G为叶盘系统中干摩擦力矢量。各矩阵表达式为
M=diag(m1,m2,…,mn,…,m2n)
C=[Cb,-Cb;Cb,Cc],Cb=diag(c1,c2,…,cn)
Cc=diag(c1+c1+n,c2+c2+n,…,cn+c2n)
K=[Kb,-Kb;Kb,Kc],Kb=diag(k1,k2,…,kn)
k(n,n)=ki+kn+i+2kg;刚度矩阵中耦合刚度kg随间隙变化而变化。
X=(x1,x2,…,xn,…,x2n)T
2叶盘系统振动局部化研究
失谐叶盘结构振动局部化主要反映在模态局部化及振动响应局部化。通过对比叶盘结构失谐前后的模态振型分析模态局部化现象,用振幅放大系数定量描述振动响应局部化程度,并对比线性、非线性系统叶盘结构的振动响应局部化程度。
2.1线性谐调叶盘系统固有频率特征分析
忽略式(6)中气流激振力及摩擦力,取kg为定值,得线性谐调叶盘系统自由振动方程为
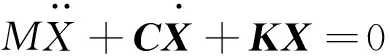
(7)
谐调叶盘系统中各扇区叶身及榫头质量、刚度、阻尼参数均一致。用文献[23-24]的叶盘结构参数,谐调系统中叶身等效质量mi=1.14×10-2kg,等效刚度ki= 4.303×105N/m,等效阻尼ci=8 N·s/m;榫头等效质量mi+n=4.27×10-2kg,等效刚度ki+n=1.735×107N/m,等效阻尼ci+n=5 N·s/m;记系统耦合强度为R=kg/ki+n,R=1.78表示强耦合系统, 刚度为kg= 3.084×107N/m;R=0.4表示弱耦合系统, 刚度为kg= 6.94×106N/m。取叶片数n=12进行数值计算。
该系统共有24个自由度,由式(7)获得24阶固有频率(Hz),其与模态阶次关系见图3。对强、弱耦合的谐调叶盘系统特征值除第1、12、13、24阶各对应一个特征值外,其它各阶固有频率均有重频出现,对应一对正交振型。文献[3]认为模型频率结构有3个典型频段,中间频段模态密集性质由叶身间弱耦合所致。而本文模型固有频率图显示无论弱、强耦合系统,固有频率均分为两频段。其中第1~12阶为低阶频段,第13~24阶为高阶频段,两频段间频率差异明显。本文单扇区简化为叶身、榫头自由度,而文献[3]模型的单扇区则简化为叶片、轮盘自由度。因此固有频率特征由系统简化模型而定,并非集中参数叶盘模型固有频率特征曲线均有3个频段。强、弱耦合系统低阶频段模态密度均较高,说明模态密集性质不一定由叶身间弱耦合导致。对强耦合系统,低阶频段固有频率集中在964.8~976.26 Hz,接近单独叶身固有频率,其模态振型由叶身主导。此低阶频段模态密集性质易导致失谐周期结构的模态局部化,为研究失谐叶盘结构振动局部化重点频段。
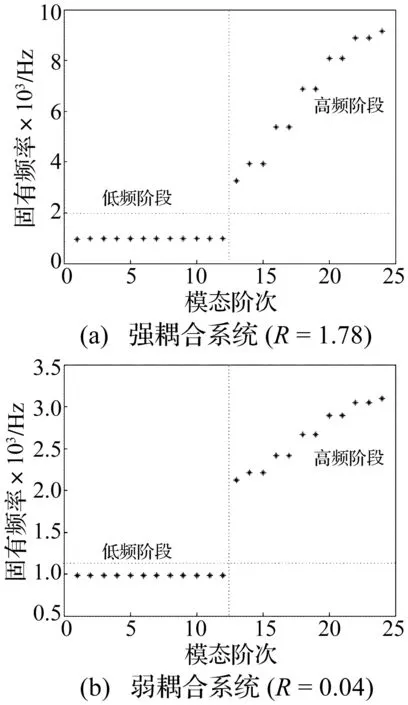
图3 谐调叶盘系统固有频率特性Fig.3 Natural frequencies of tuned bladed disk systems with strong
2.2线性失谐叶盘系统模态振型局部化
考虑叶身刚度失谐,定义第i个叶身刚度失谐强度为ρi=(ki-kb)/kb, 其中kb为谐调叶盘系统叶身等效刚度;ki为失调叶盘系统各叶身刚度。则失谐后各叶身刚度值满足ki=kb(1+ρi)。取失谐强度ρ满足均值为0、标准差分别为σ1=0.02、σ2=0.04、σ3=0.06、σ4=0.08的随机正态分布,生成4组失谐强度随机数见表1。
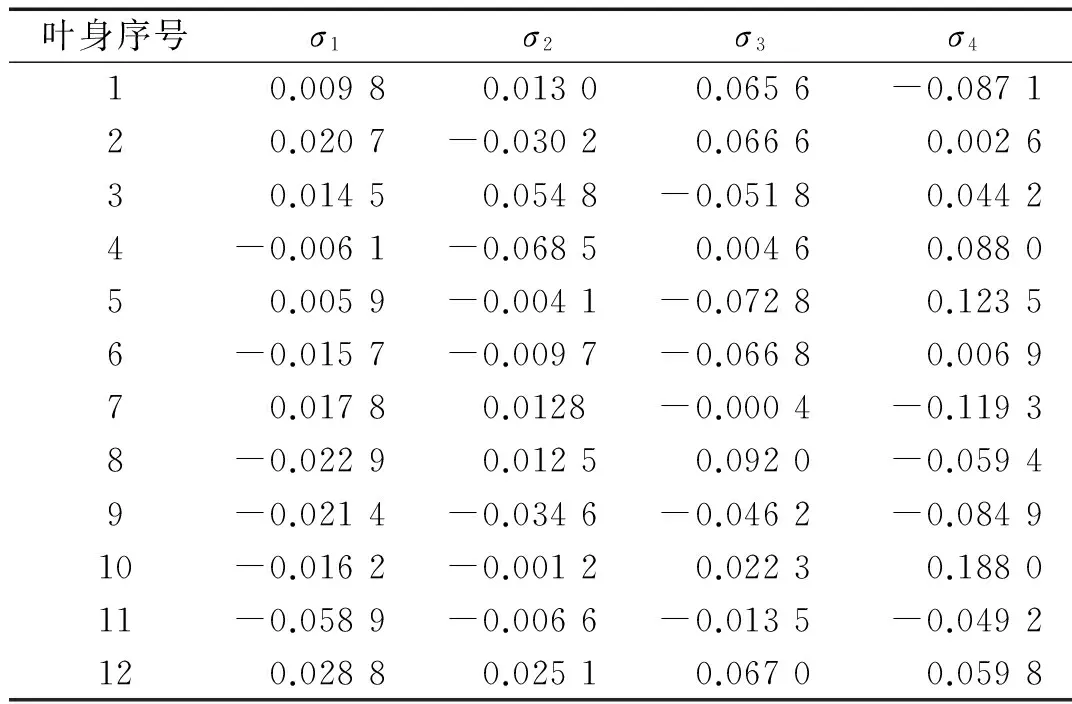
表1 叶身刚度失谐强度值
分析R=1.78的强耦合系统。选第2、18阶固有频率求解得系统对应的模态振型。低阶频段对应模态振型为叶身主导振型,故叶身的振动幅值远大于榫头。因主要研究不同失谐量对模态振型影响,故只选叶身的相对振幅进行比较。谐调、失谐状态下模态振型见图4~图6。
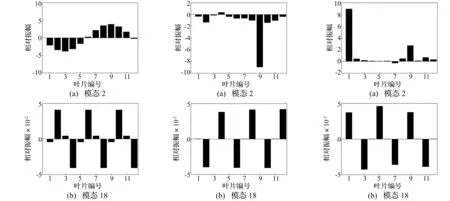

图4 谐调叶盘系统模态振型Fig.4Modeshapesofthetunedbladeddisksystem图5 失谐叶盘系统模态振型(σ1=0.04)Fig.5Modeshapesofthemistunedbladeddisk(σ1=0.04)图6 失谐叶盘系统模态振型(σ1=0.08)Fig.6Modeshapesofthemistunedbladeddisk(σ1=0.08)
由图4看出,谐调叶盘系统模态振型均呈谐和形式,叶身振幅呈正弦或余弦变化形式。系统模态振动能量在叶盘的分布呈均匀式,无模态局部化现象产生。由图5、图6看出,失谐叶盘系统模态振型出现局部化。第18阶模态振型局部化不很明显,第2阶模态振型出现强烈的局部化现象,模态振型中一个叶身振幅远大于其它叶身。因低阶频段模态振型由叶身主导,而高阶频段模态振型由榫头主导,故叶身刚度失谐对低阶频段模态振型影响较大。在叶身主导振动下,失谐更易致振动能量在叶盘上呈不均匀分布,且低阶频段模态密集性质亦易导致失谐叶盘系统的模态局部化。此与对叶盘系统固有频率特性分析一致。
2.3非线性失谐叶盘系统的振动响应局部化
式(6)为谐调叶盘结构模型,其中叶身等效刚度均相等,即k1=k2=…=kn=kb,失谐叶盘系统各叶身刚度值不相等,满足ki=kb(1+ρi),ρi为第i个叶身刚度失谐强度。取间隙d0=0.8 mm。依次取失谐强度ρ满足表1中4组随机正态分布,将叶身刚度失谐量加入式(6),分析非线性失谐叶盘系统振动响应,与谐调系统进行对比。
因榫头处干摩擦力、间隙作用对榫头运动影响较对叶身影响大,故分析失谐对榫头响应影响。对强耦合系统,分别以第2、18阶固有频率值作为气流激振力的激振频率进行共振响应分析,计算得到每个榫头最大振动位移。
谐调叶盘系统为周期循环结构,在相同外部激励下,每个叶身沿圆周方向相同位置振动响应相同。图7的蓝色曲线为谐调叶盘系统每个叶身最大振动位移,其余则为不同失谐强度下每个叶身最大振动位移。由图7看出,第2、第18阶共振系统叶身振幅不一致,呈振动局部化现象。第18阶的振动响应局部化程度较第2阶弱。对高阶频段共振,失谐强度对振动局部化影响较复杂。因高阶频段共振属于榫头共振区,而榫头又受摩擦及间隙影响,导致失谐对系统运动影响较复杂。榫头主导的第18阶共振下含干摩擦、间隙的非线性谐调叶盘系统亦出现振动响应局部化现象。此由间隙与摩擦力非线性力作用所致。说明振动能量局部化不仅由失谐引起,非线性因素亦能引起。此与含非线性刚度的谐调叶盘系统[25]及含非线性摩擦阻尼的谐调叶盘系统振动局部化现象一致。
2.4失谐叶盘系统振幅放大系数
为进一步描述失谐叶盘系统振动响应局部化程度,引入振幅放大系数AMF
(8)
式中:Umax,Vmax为同工况下失谐、谐调叶盘结构叶身(或榫头)振幅最大值。
考虑强耦合系统中不同叶身刚度的随机失谐对系统强迫振动响应影响。取2.1节的各阶固有频率值, 取激励力频率为系统各阶固有频率,计算各阶共振下系统的叶身、榫头振幅放大系数。
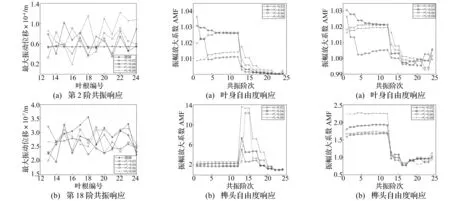

图7 叶身刚度失谐下的榫头响应Fig.7Resonanceresponseofthetenonunderbladebodystiffinessmistuning图8 线性系统中叶身刚度失谐下振幅放大系数Fig.8AMFofthelinearsystemwithbladebodystiffinessmistuning图9 非线性系统中叶身刚度失谐下振幅放大系数Fig.9AMFofthenonlinearsystemwithbladebodystiffinessmistuning
2.4.1线性失谐叶盘系统
计算线性系统叶身、榫头在气流激振力下的振动响应,利用方式(8)计算各自振幅放大系数,见图8。由图8看出,两者振幅放大系数在频段交界处均发生突变。叶身刚度失谐对叶身响应影响主要集中在低阶频段, 而对榫头影响主要集中在高阶频段。因低阶频段频率更接近单独叶身固有频率,使叶身对失谐更敏感。同样,榫头在高阶频段共振下对失谐亦更敏感。对叶身响应的低阶频段,振幅放大系数随失谐强度先增加到一定程度又随失谐强度进一步增加而减小。即出现失谐“阈值”现象,与文献[6,9-10]研究结果一致。榫头在第13、14、15阶共振响应下的振幅放大系数大于其它阶共振响应对应值。因该三阶固有频率更接近单独榫头固有频率,故在此阶共振响应下对失谐更敏感。
2.4.2非线性失谐叶盘系统
计算非线性系统叶身、榫头自由度振动响应,并用式(8)计算各自振幅放大系数,结果见图9。在叶身响应低阶频段,振幅放大系数亦出现失谐“阈值”现象。而对榫头响应,振幅放大系数在高阶频段随失谐强度变化更复杂。两者振幅放大系数在高阶频段均出现小于1的值,即失谐系统最大振幅较谐调系统小。此因非线性摩擦、间隙作用降低失谐叶盘系统振动局部化程度。对比图8(b)、图9(b)知,非线失谐叶盘系统振幅放大系数远小于线性失谐叶盘系统。说明对失谐叶盘系统,干摩擦、间隙等非线性因素的存在会改善振动局部化现象。实际叶盘系统为非线性,而结构失谐难以避免。故可进一步推测,对非线性系统,合理的人为失谐设计能减小叶盘系统对失谐的敏感性。即通过优化寻找具有减振效果的失谐方式。
3叶盘系统非线性响应分析
对含齿侧间隙的齿轮系统进行动力学分析时,陈广艳等[26-27]认为在不同激励频率下系统会出现简谐、非简谐单周期、多周期次谐波及混沌等稳态强迫响应。因榫头处间隙、干摩擦的存在,本文叶盘系统亦出现类似的复杂非线性特性。因此,对比叶盘系统单周期运动状态下失谐、谐调叶盘系统幅频响应特征。
3.1谐调叶盘系统非线性响应分析
因谐调叶盘系统为循环周期结构,且受到有一定相位差的相同外部激励,研究整体叶盘结构非线性特性时只取某个扇区的计算结果进行分析。对强耦合系统中榫头集中质量块进行共振响应分析,研究摩擦、间隙等非线性因素对系统动力学响应影响。
3.1.1只含干摩擦的非线性系统振动响应分析
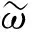
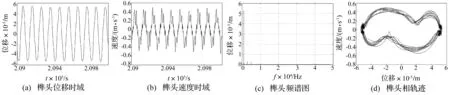
图10 含干摩擦非线性系统榫头响应Fig.10 Response of the tenon of the nonlinear system with dry friction
3.1.2同时含干摩擦、间隙的非线性系统响应分析
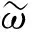
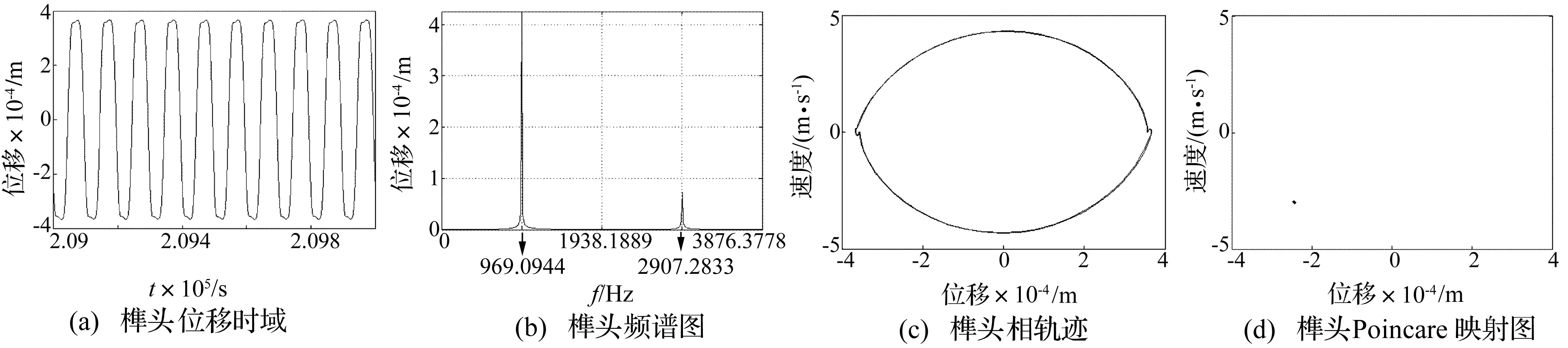
图11 同时含间隙、干摩擦非线性系统榫头自由度响应=969.09 Hz)Fig.11 Response of the tenon of the nonlinear system with dry friction and gap
3.1.3非线性系统随激励力频率变化的动力学行为
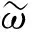

图时非线性系统榫头响应Fig.12 Response of the tenon of the nonlinear system

图时非线性系统榫头振动响应Fig.13 Response of the tenon of the nonlinear system
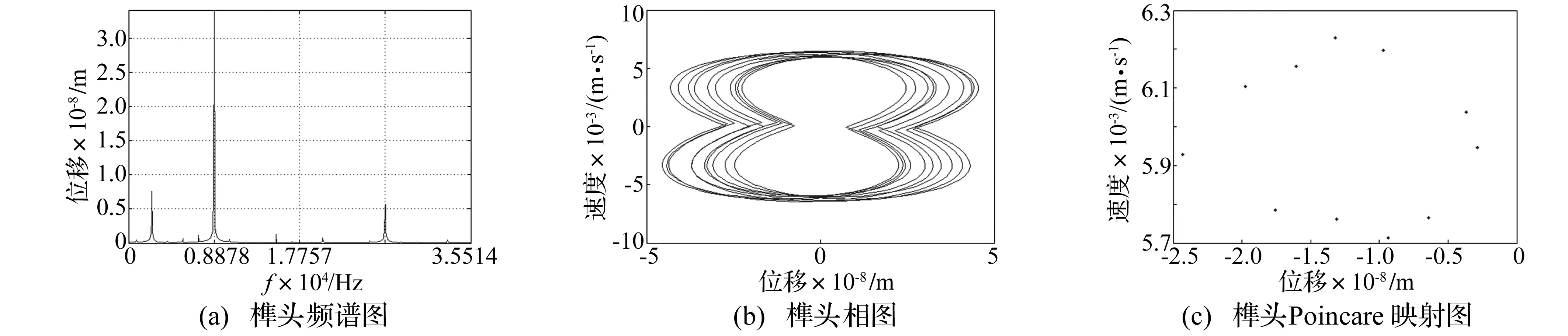
图时非线性系统榫头振动响应Fig.14Response of the tenon of the nonlinear system
结合图11~图14可知,在间隙、摩擦因素影响下,系统从混沌运动进入非简谐单周期运动再进入多周期谐波运动,动力学行为非常复杂。混沌响应及多周期谐波响应对叶盘系统稳定性均不利,故将叶盘系统的工作状态控制在单周期运动附近较合理。
3.2失谐叶盘系统非线性响应分析
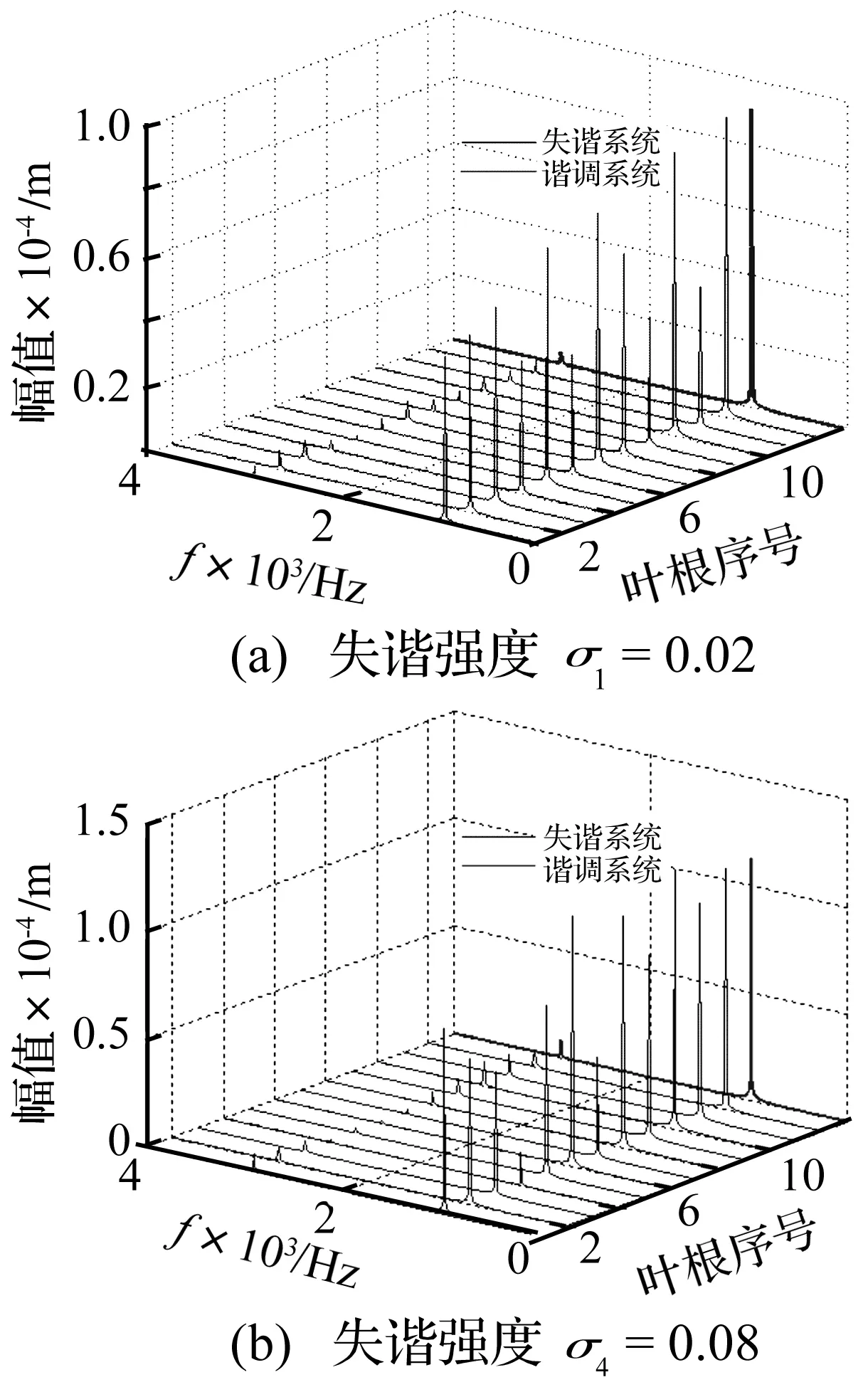
图15 不同失谐强度下叶盘系统幅频响应Fig.15 The amplitude frequency response of bladed disk system under different mistuning strength
实际系统中的摩擦、间隙等非线性因素及结构小量失谐均无法避免,因此合理人为设计某种叶身失谐形式,能减小叶盘系统对失谐的敏感性。分析表明,非线性谐调叶盘系统动力学行为较复杂,若再引入失谐因素,非线性失谐叶盘系统动力学行为会更复杂。
4结论
通过首次建立含间隙与摩擦的叶盘系统模型,研究叶身刚度随机失谐下叶盘系统模态振型及振动响应局部化,分析非线性叶盘系统动力学行为,结论如下:
(1) 强、弱耦合系统固有频率结构均有两个频段,且低阶频段模态密度较高,即模态密集性质不一定由叶身间弱耦合引起。
(2) 含摩擦与间隙的非线性谐调叶盘系统出现的振动局部化现象表明,振动响应局部化不仅仅由于失谐,摩擦、间隙等非线性因素亦能引起局部化。
(3) 线性/非线性失谐叶盘系统振幅放大系数均出现失谐“阈值”。非线系统振幅放大系数远小于线性系统,表明干摩擦、间隙等非线性因素存在会改善失谐产生的振动局部化;该放大系数小于1,表明摩擦、间隙作用会降低失谐叶盘系统振动局部化程度。
(4) 非线性谐调叶盘系统随外激励力频率变化的响应会呈非简谐单周期、多周期谐波及混沌运动等动力学行为。非线性失谐叶盘系统动力学行为更复杂。合理的人为失谐设计能减小叶盘系统对失谐的敏感性。
参 考 文 献
[1] 白斌,白广忱,童晓晨,等. 整体叶盘结构失谐振动的国内外研究状况[J]. 航空动力学报, 2014,29(1):91-103.
BAI Bin, BAI Guang-chen, TONG Xiao-chen, et al. Research on vibration problem of integral mistuned bladed disk assemblies at home and abroud[J]. Journal of Aerospace Power, 2014,29(1):91-103.
[2] 臧朝平,兰海强. 失谐叶盘结构振动问题研究新进展[J]. 航空工程进展, 2011,2(2):133-142.
ZANG Chao-ping, LAN Hai-qiang. Advances in research vibration problem of mistuned blisk assemblies[J]. Advances in Aeronautical Science and Engineering,2011,2(2):133-142.
[3] 王建军,李其汉. 航空发动机失谐叶盘振动减缩模型与应用[M]. 北京: 国防工业出版社, 2009.
[4] 王红建. 复杂耦合失谐叶身-轮盘系统振动局部化问题研究[D]. 西安: 西北工业大学, 2006.
[5] Castanier M P, Pierre C. Modeling and analysis of mistuned bladed disk vibration: current status and emerging directions [J]. Journal of Propulsion and Power, 2006,22(2):384-396.
[6] Castanier M P, Pierre C. Using intentional mistuning in the design of turbomachinery rotors[J]. AIAA Journal, 2002, 40(10): 2077-2086.
[7] 王建军,于长波,姚建尧,等. 失谐叶盘振动模态局部化定量描述方法[J]. 推进技术, 2009,30(4): 457-461.
WANG Jian-jun,YU Chang-bo,YAO Jian-yao, et al. Vibratory mode localization factors of mistuned bladed disk assemblies [J]. Journal of Propulsion Technology, 2009,30(4): 457-461.
[8] 王培屹,李琳. 叶盘结构盘片耦合振动特性的参数敏感性[J]. 航空动力学报, 2014,29(1):81-90.
WANG Pei-yi, LI Lin. Parametric sensitivity for coupling vibration characteristics of bladed disk[J]. Journal of Aerospace Power, 2014,29(1):81-90.
[9] Choi B K, Lentz J, Rivas Guerra A J, et al. Optimizations of intentional mistuning patterns for the reduction of the forced response effects of unintentional mistuning[J]. Journal of Engineering for Gas Turbines and Power, 2003,125(1): 131-140.
[10] Wei S T, Pierre C. Statistical analysis of the forced response of mistuned cyclic assemblies[J].AIAA Journal, 1990, 28(5): 861-868.
[11] 刘长福,邓明. 航空发动机结构分析[M]. 西安: 西北工业大学出版社, 2006.
[13] Sinclair G B, Cormier N G. Contact stresses in dovetail attachments: alleviation via precision crowning[J]. Journal of Engineering for Gas Turbines and Power, 2003,125(4):1033-1041.
[14] Sinclair G B, Cormier N G. Contact stresses in dovetail attachments physical modeling[J]. Journal of Engineering for Gas Turbines and Power, 2002,124(2):325-331.
[15] Sinclair G B, Cormier N G, Griffin J H, et al. Contact stresses in dovetail attachments: finite element modeling[J]. Journal of Engineering for Gas Turbines and Power, 2002,124(1):182-189.
[16] Petrov E P. A method for use of cyclic symmetry properties in analysis of nonlinear multiharmonic vibrations of bladed disks[J]. Transactions of the ASME-T-Journal of Turbomachinery, 2004,126(1):175-183.
[17] 张亮,袁惠群,韩清凯,等. 基于微动滑移摩擦模型的失谐叶盘系统振动分析[J]. 振动工程学报, 2012,25(3):289-293.
ZHANG Liang, YUAN Hui-qun, HAN Qing-kai, et al. Vibration analysis of mistuned bladed disk system based on microslip friction model[J]. Journal of Vibration Engineering, 2012,25(3):289-293.
[18] 王艾伦,龙清. IHB方法在含强非线性摩擦力失谐叶盘系统响应特性研究中的应用[J]. 机械强度, 2012,34(2):159-164.
WANG Ai-lun, LONG Qing. Application of IHB method to study the response characteristics of mistuning bladaded disks with strong non-linear friction[J]. Journal of Mechanical Strength, 2012,34(2):159-164.
[19] 王艾伦,龙清. 具有非线性摩擦阻尼随机失谐的叶盘系统响应特性[J]. 航空动力学报, 2011,26(1):178-184.
WANG Ai-lun, LONG Qing. Forced response characteristics of bladed disks with random mistuned non-linear friction damping[J]. Journal of Aerospace Power, 2011,26(1):178-184.
[20] Petrov E P. Analysis of flutter-induced limit cycle oscillations in gas-turbine structures with friction, gap, and other nonlinear contact interfaces[J]. Journal of Turbomachinery, 2012, 134(6):061018-061030.
[21] Berthillier M, Dupont C, Mondal R. Blades forced response analysis with friction dampers[J]. Journal of Sound andVibration, 1989,129(3):397-416.
[22] Wei S T, Pierre C. Effect of dry friction damping on the occurrence of localized forced vibration in nearly cyclic structures[J]. Journal of Vibration and Acoustics, 1998,120:468-474.
[23] Griffin J H, Hoosac T M. Model development and statistical investigation of turbine blade mistuning[J]. Journal of Vibration, Acoustics Stress and Reliability in Design, 1984, 106(2): 204-210.
[24] Ghiocel D M, Kirsch U. Combined approximations for efficient probabilistic analysis of structures[J]. AIAA Journal, 2004,42(7):1321-1330.
[25] Georgiades F, Peeters M, Kerschen G, et al. Modal analysis of a nonlinear periodic structure with cyclic symmetry[J].AIAA Journal, 2009,47(4):1014-1025.
[26] 陈广艳, 陈国定,李永祥,等. 考虑齿侧间隙影响的直齿面齿轮传动动力学分析[J]. 机械科学与技术, 2009,28(9):1244-1251.
CHEN Guang-yan, CHEN Guo-ding, LI Yong-xiang, et al. Dynamic analysis of a face-gear drive with spur involute pinion with bachlash considered[J]. Mechanical Science and Technology for Aerospace Engineering,2009,28(9):1244-1251.
[27] 孙智民,季林红,沈允文. 2K-H 行星齿轮传动非线性动力学[J]. 清华大学学报:自然科学版, 2003,43(5):636-639.
SUN Zhi-min, JI Lin-hong, SHEN Yun-wen. Nonlinear dynamics of 2K-H planetary gear train[J]. Journal of Tsinghua University:Science and Technology,2003,43(5):636-639.
基金项目:国家重点基础研究发展计划(2015CB057400);天津市自然科学基金项目(11JCZDJC25400)
收稿日期:2014-10-10修改稿收到日期:2014-11-26
通信作者曹树谦 男,博士,教授,博士生导师, 1964年生
中图分类号:V231
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.02.014
Vibration localization of a mistuned bladed disk system with friction and gap
ZENG Hai-nan1,2, CAO Shu-qian1,2, SU Yong-lei3
(1. School of Mechanical Engineering, Tianjin University, Tianjin 300072, China;2. Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin 300072, China;3. CAE Department-Changan Auto Global R & D Center, Chongqing 401120, China)
Abstract:Based on the lumped parameter model of a bladed disk, the vibration localization of a mistuned bladed disk was investigated in consideration of nonlinear parameters such as dry friction and gap in connections between blade tenton and mortise. For systems with different coupling stiffness, the natural frequencies and resonance responses were discussed under random mistuning of the blades stiffnesses. The results show that the vibration localization would also appear in the tuned system with nonlinear factors. Using the amplitude magnification factor (AMF), the vibration response localization of linear and nonlinear mistuned bladed disks was explored, and the existence of an AMF’s threshold was uncovered. The degree of vibration response localization of the mistuned system will reduce because of the participation of nonlinear dry friction and gap. The analysis of nonlinear tuned system under different excitation frequencies turns to reveal the nonlinear dynamics behaviors such as non-harmonic periodic-one motion, multi-period harmonic motion and chaotic motion of the system. Besides, as the mistuning factor exists, the behaviors of nonlinear mistuned disk systems become more complex.
Key words:bladed disk system; mistuning; vibration localization; dry friction; gap; amplitude magnification factor; nonlinear dynamics
第一作者 曾海楠 女,硕士生,1989年生
邮箱: sqcao@tju.edu.cn

