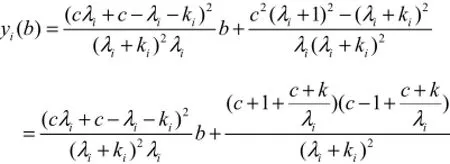对线性回归模型新有偏估计 β∗= （K， c）的进一步讨论

隋丹阳鄂英力辽宁装备制造职业技术学院 （沈阳 06）高明实验学校 （沈阳 0000）



对线性回归模型新有偏估计 β∗= （K， c）的进一步讨论

隋丹阳1鄂英力2
1辽宁装备制造职业技术学院 （沈阳 110161）2高明实验学校 （沈阳 110000）

摘 要在线性回归模型 Y= X β+ ε；E（ε） = 0；cov = σ2Σ； Σ ＞0下给出了有偏估计β∗（K，c）= c（ XTΣ¯1X + K）¯1（XTΣ¯1Y +β∗），其中 K ＞ 0，c＞ 0为参数，β∗表示线性回归模型的广义最小二乘估计，讨论了这种有偏估计的优良性质，得出了主要结论。

关键词有偏估计；广义最小二乘；岭估计

1 考虑线性回归模型

X为已知列满秩矩阵， Y = n×1为可观测的随即向量，β为 p×1未知参数向量， r（ X ）= p ≤ n，σ2＞0为未知参数，ε为 n×1随机误差向量。 In为n阶单位矩阵， E（ε）表示ε的均值向量，cov（ε）表示ε的协方差矩阵。在模型（1）中给出典则交换Z = XQ，典则参数α = QTβ，其中Q为p阶正交矩阵，其列向量为 XTX的特征向量，Λ = diag （λ1， λ2，"，λp），λj≥0（j =1，2，"，p）为XTX的特征根。则模型（1）化为典则形式：

2 β∗（K， c）的提出

本文将模型推广到奇异线性模型中：

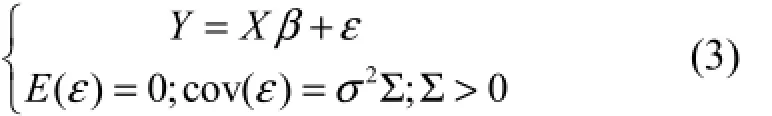
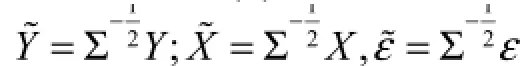
考虑模型（6）的典则形式：设λ≥ λ ≥ " ≥λ为

12pXTX = XTΣ¯1X的特征根，t1， t2，" ，tp为相应的标准正交化特征向量。记 T = （t1，"，tp），Λ =diag（λ1， " ，λp），则有Y = Zα+。这里 Z = XT ，α = TTβ.因为ZTZ = TTXTXT =Λ，所以 α∗= TTβ∗=Λ¯1ZTY.

我们将对广义岭估计做进一步改进，给出模型（5）的一个新估计：

3 β∗（K， c）的均方误差和均方残差

通过计算我们发现当MSE逐渐减少的同时，对模型拟合的均方残差（MSR）却在增大，这与我们期望的相反。下面通过计算来讨论MSE和MSR的变化情形［1］。考虑估计：

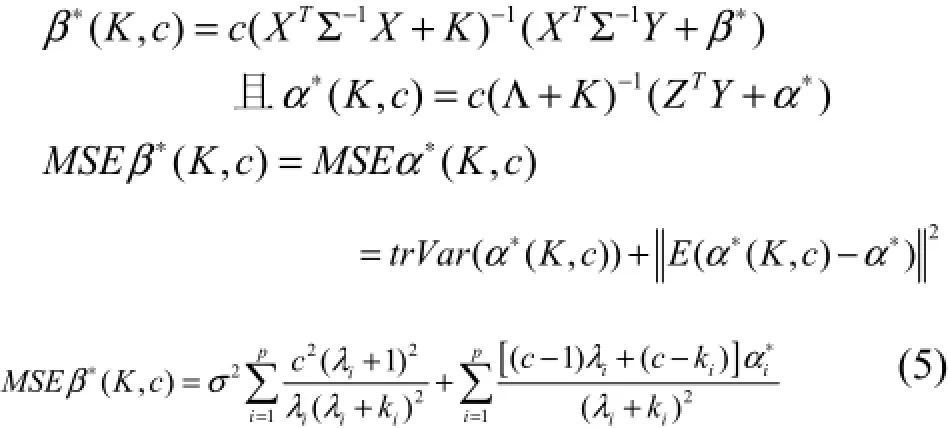
显然 MSEβ∗（K， c）是（ki， c）的二元连续函数，且满足隐函数定理［2］的一切条件。

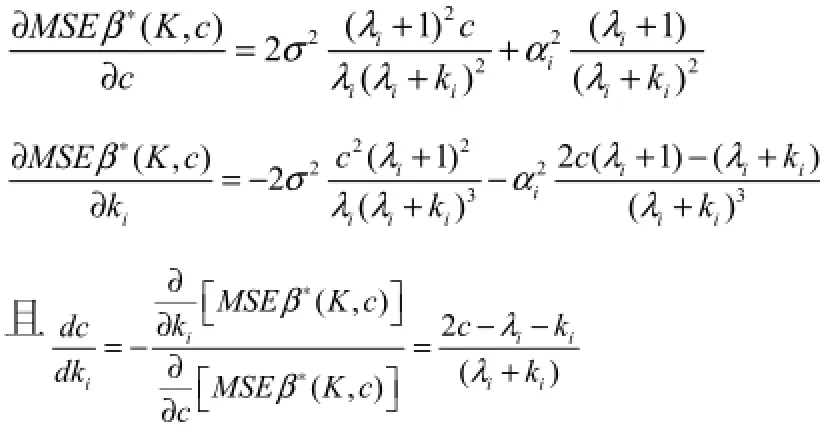
这说明c与 λi+ ki之间有线性关系。令上述两个偏导数分别等于零，得

可以判断 MSEβ∗（K， c）在（c∗， ki∗）处取得最小值，且

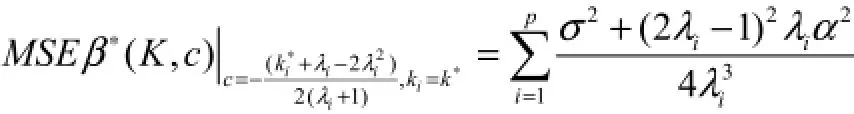
当c→∞或 k→∞时，

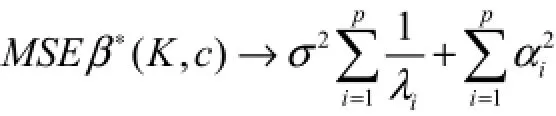
其中 MSR（β∗）为β∗的均方残差， ΔMSRβ∗（K， c）为 β∗（K， c）对β∗修正后产生的平均增量，对于MSR（β∗）已熟知，故只讨论 ΔMSRβ∗（K， c）。

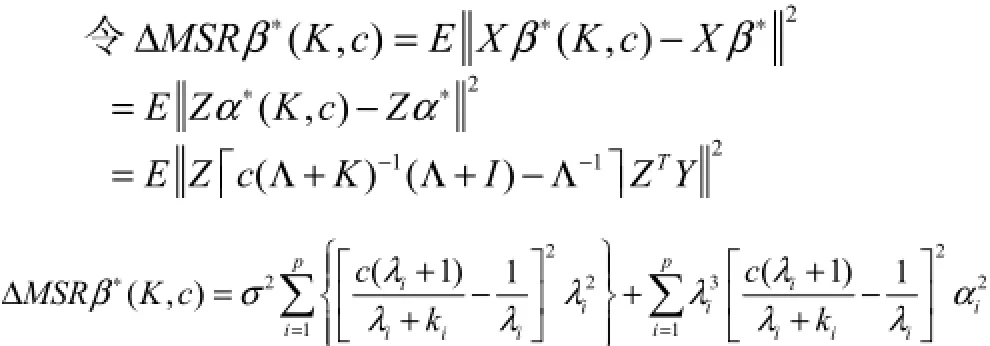
4 β∗（K， c）的可容许性

引理［3］：模型（5）中，在二次损失（d ¯β）T（d ¯β）下，LY在线性估计类中是β的可容许估计的充分必要条件是：

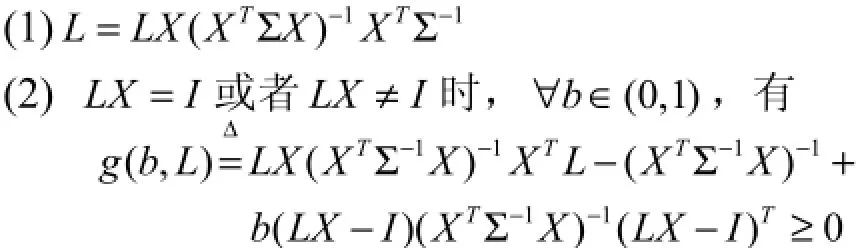
不成立。

定理：模型（5）在均方误差意义下在线性估计类中，当r（ X ）= p， Σ＞ 0，β∗（K， c） = c（ XTΣ¯1X + K ）¯1（XTΣ¯1Y + β∗）是β的可容许估计的充要条件为0 < ki

证明：充分性在文献［4］中已证，下面主要证明必要性。

因为LY为可容许估计，所以 ∀b ∈ （0，1），g（ b， L）不是半正定阵，T为正交阵，即 ∀b ∈ （0，1），TTg（ b， L） T 不是半正定阵，令

因为 ∀b ∈ （0，1），TTg（ b， L） T 不是半正定阵，

所以， ∀b ∈（0，1），min ｛y1（ b） ，y2（ b） ，"，yp（b） ｝<0

则0

min ｛y1（ b ），y2（ b） ，"，yp（b ）｝= y1（ b）＞0

则 ∀b ∈ （0，1），TTg（ b， L） T 半正定，矛盾。

所以， β∗（K， c） =c（ XTΣ¯1X + K ）¯1（XTΣ¯1Y +β∗）是β的可容许估计的充要条件为0 < ki

参考文献

［1］腾素珍，王志福.对泛岭古迹的最优准则的进一步讨论［J］.大连理工大学学报，1994，9（2），42-47.

［2］华东师范大学数学系编.隐函数定理及其应用（数学分析下册）第三版［M］.北京：高等教育出版，2001.

［3］王松佳.线性模型的理论及应用［M］.合肥：安徽教育出版社.1987.

［4］张玮，刘禄勤.线性回归模型的一种有偏估计［J］.武汉大学学报（理学报），2006，6（3）：281-281

（责任编辑：文婷）

中图分类号：O1-0

文献标识码：A

文章编号：1003-3319（2016）01-00013-02