考虑相对论修正后的氢原子能级

张翠萍本溪广播电视大学 （本溪 117000）



考虑相对论修正后的氢原子能级

张翠萍
本溪广播电视大学 （本溪 117000）

摘 要本文对自由粒子按照相对论的理论修正后，利用薛定谔方程对氢原子的能级进行了推导。

关键词粒子能量；薛定谔方程；氢原子能级

1 能级的一级修正

量子力学中，按照相对论理论，自由粒子的能量为：

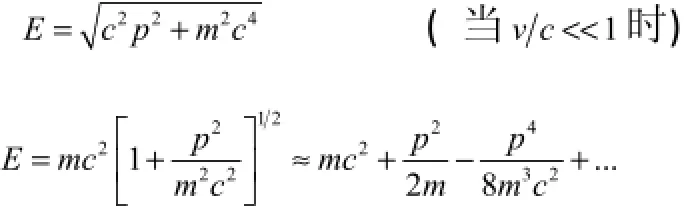
去掉 mc2后，考虑到相对论修正的首项，则氢原子的哈密顿量可以表示为：

把W看成微扰，则：

本征值为：

因为：

所以：

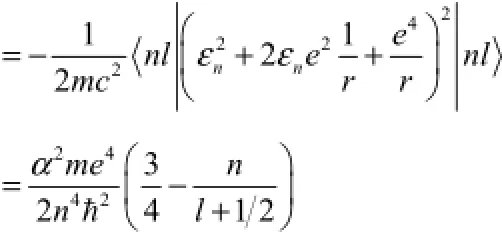
2 考虑相对论修正后的薛定谔方程

按照上边的思路，对于薛定谔方程：

3 考虑相对论修正后的薛定谔方程

按照上边的思路，对于薛定谔方程：

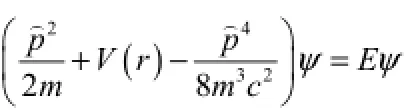
于是，薛定谔方程就变为：

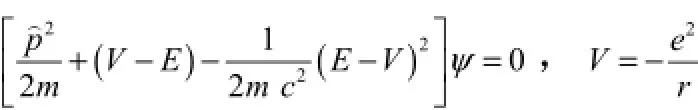
考虑相对论修正后的氢原子能级

对薛定谔方程做一下形式上的改变：

则R（ r）满足的径向方程为：

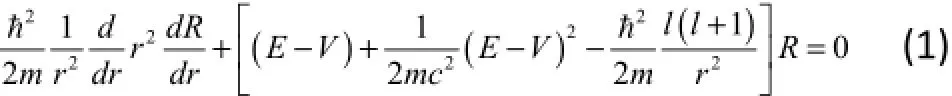
则： 满足e2，令： ，代入式（1），得：

R（ r）rP= rR

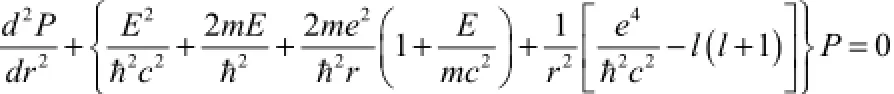
为书写方便，将上面的方程写成如下形式：

考虑有界性，在r=∞附近为e¯¯Ar，以级数解代入原点 r =0处的渐进方程：

得到级数的最低次幂是 rν，ν由下式确定：

由上式解出：

考虑到当c→∞时的结果应与相对论的结果（ν =l）相一致，那么，解只能取ν+。解为：

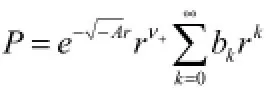
将其代入式（2）中，得出系数递推公式：

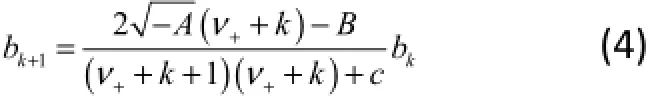
除非E取本征值将级数截断为多项式，级数

∑ bkrk将以e2¯Ar的行为发散。

令： bS +1=0，则由式（4）可导出含有E的公式：

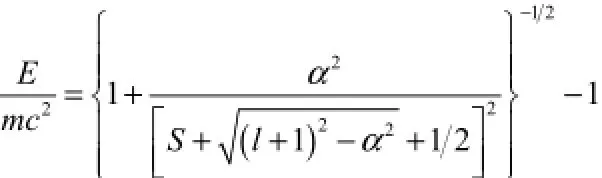
我们要做的就是在c→∞时，将上式右端的根式中的 α2展开。

4 结论

将上式展开后，得到公式：

此式即为考虑相对论修正后的氢原子的能级。

参考文献

［1］曾瑾言.量子力学［M］.北京：科学出版社，1981.

［2］徐寿绵.高等量子力学［M］.青岛：山东科学技术出版社，1985.

［3］比约肯，德雷尔.相对论量子场［M］.北京：科学出版社，1984.

中图分类号：O411.1

文献标识码：A

文章编号：1003-3319（2016）02-00011-02