径向加载工况下的第3代轮毂轴承动力学分析

林棻，沈元杰，王伟

(南京航空航天大学 车辆工程系，南京 210016)

轮毂轴承是汽车的重要零部件，对车辆安全性及舒适性至关重要。目前轿车上广泛使用第3代轮毂轴承[1]，即内、外圈都带凸缘，通过内、外凸缘连接车轮与车身。随着对轮毂轴承的性能要求越来越高，其结构也在不断改进[2]。

汽车行驶时，轮毂轴承的内圈高速运转，工况复杂，尤其是动应力对轴承的寿命有着很大影响，因此有必要分析轮毂轴承的动态特性。目前，针对第3代轮毂轴承的动力学研究较少，文献[3]采用静力学分析验证轮毂轴承建模和轻量化设计的合理性，但并未通过动力学进行验证；文献[4]分别选用弹性材料模型以及塑性材料模型，分析滚子轴承不同载荷下的运动状态；文献[5]利用数值方法对轴承的内部动力学状态进行数值模拟仿真；文献[6]将多体动力学和有限元方法相结合进行轴承动力学计算；文献[7]采用拟静力学方法分析了球轴承的力学特性。

文中以某型汽车第3代轮毂轴承作为研究对象，分别建立低、中、高速行驶状态下的轮毂轴承有限元模型，并进行显式动力学仿真，精确分析轮毂轴承的动态特性。

1 轮毂轴承载荷计算

径向载荷通过轮胎间接施加在轮毂轴承上。文中研究工况为平直路面匀速行驶，故可认为轮胎所受载荷等于轮毂轴承的径向载荷。第3代轮毂轴承所受外载荷如图1所示。为便于分析外载荷对2列钢球的作用，将径向载荷转化为分别作用于2列沟道处的作用力。其力学关系为

Fe+Fi=Fr，

(1)

Fe(L1+e)-Fi(L2-e)=0，

(2)

式中：Fr为轮毂轴承径向载荷；Fe，Fi为径向载荷Fr分解至外、内列沟道处的作用力；L1，L2为Fe，Fi与轮毂轴承中心线的距离；e为偏移量。由于沟道接触角，轮毂轴承还受到径向载荷所产生的附加轴向载荷Fae和Fai，但该载荷由径向载荷所派生，在后文的仿真中不直接体现在边界条件中。

图1 第3代轮毂轴承载荷示意图

2 有限元模型

某型汽车第3代轮毂轴承的结构参数见表1。

表1 结构参数

2.1 模型简化

针对轮毂轴承的运动特点，做如下假设：由于轮毂轴承自由端的倒圆及倒角对轮毂轴承内部应力影响较小，可忽略；不考虑游隙对轮毂轴承的影响。采用CATIA建立轮毂轴承简化模型如图2所示。

图2 几何模型

2.2 网格划分

用六面体网格对轮毂轴承进行划分，并将接触区域进行网格细化。最终网格数目为180万，部分结构网格模型如图3所示。

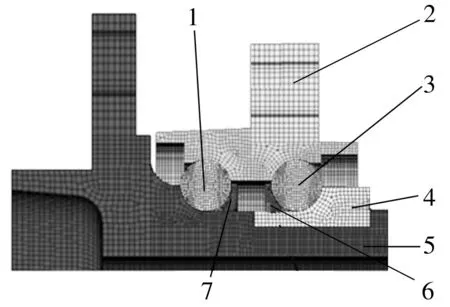
1—外列钢球；2—外凸缘；3—内列钢球；4—内圈；5—内凸缘；6—内列保持架；7—外列保持架

2.3 材料特性

第3代轮毂轴承属于带有内、外凸缘的双列角接触球轴承，结构复杂，网格数目庞大。将内、外凸缘的沟道部位定义为线弹性体，其余部位定义为刚体，既提高了计算效率，又便于分析接触应力。由于钢球的应变最大，保持架的变形相对较小，因此定义保持架为刚体，钢球为线弹性体。内、外凸缘的材料为55#钢，内圈、钢球及保持架的材料为GCr15，材料参数见表2。

表2 材料参数

2.4 接触模型

轮毂轴承作为高度非线性模型，存在较多接触,选择自动面面接触，设置相应的摩擦因数。由于轮毂轴承实际工作在油润滑、湿摩擦的条件下，故综合考虑其实际摩擦以及润滑油等因素后的摩擦因数见表3(fS为静摩擦因数，fD为动摩擦因数)。

表3 钢球及各零件的摩擦因数

2.5 边界条件

第3代轮毂轴承外凸缘与车身相连，内凸缘与制动盘相连。为真实模拟车辆在平直路面匀速行驶所受载荷，施加边界条件：1)外凸缘固定，进行全约束；2)内凸缘施加恒定转速以及径向载荷。汽车满载低速行驶，车速为40 km/h；同时对内凸缘施加4 900 N的径向载荷。由(1)式、(2)式可得Fe为1 960 N，Fi为2 940 N。

显式动力学分析中存在许多的控制卡片，如求解控制和结果输出控制等；而沙漏控制、质量缩放控制以及接触控制等则负责监控计算过程，若发现模型存在错误，随时终止计算。这些控制卡片在显式分析中必不可少，该轮毂轴承有限元模型相应的控制卡片见表 4。

表4 显式动力学求解参数

为减少计算，采用缩减积分单元，但该类型单元易引起沙漏效应，将对计算结果产生影响，因此需要进行沙漏控制。

时间步长控制，即质量缩放技术，TSSFAC代表时间步长缩放系数，默认值为0.9，当计算不稳定时，可以适当减小，但会增加计算时间。

3 结果分析

3.1 能量曲线验证

在显式动力学分析中使用缩减积分单元时，规定沙漏能不超过内能的10%。轮毂轴承有限元模型的内能与沙漏能曲线如图4所示。沙漏能占内能峰值的3.6%左右，且其他时刻沙漏能变化平稳，一直处于非常低的状态。因此可认为该分析合理。

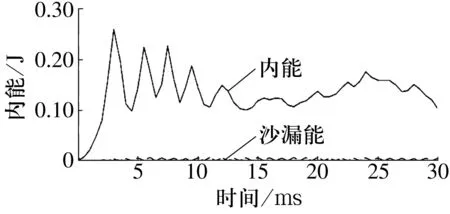
图4 内能与沙漏能曲线

3.2 速度分析及仿真验证

3.2.1 速度分析

轮毂轴承在30 ms时的速度云图如图5所示。由图可知，内凸缘速度最大，外凸缘由于施加了全约束，速度最小，几乎为0。在径向载荷的作用下，钢球与内、外凸缘及内圈之间存在摩擦力，内凸缘带动内圈、钢球和保持架同向转动。

图5 轮毂轴承速度云图

在2,30 ms时的钢球速度云图如图6所示。钢球与内凸缘、内圈接触位置速度最大，外凸缘接触位置速度最小，几乎为0。在2,30 ms时的保持架速度云图如图7所示，最大速度位于保持架外边缘。

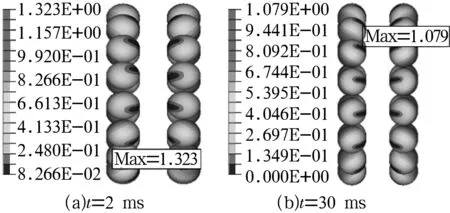
图6 双列钢球速度云图

图7 双列保持架速度云图

钢球、保持架的速度时程曲线如图8所示。在2.5 ms时刻，钢球速度达到最大，最后趋于稳定，约为1.08 m/s。内、外列钢球运转趋势基本一致，但不同时刻的速度存在微小差异。内、外列保持架的速度变化趋势也基本相同，最后趋于稳定，约为0.5 m/s。不同时刻，2列保持架速度值并不完全相同，且钢球速度明显大于保持架速度，这是由于保持架只存在公转，而钢球在公转的同时存在强烈的自转。

图8 速度时程曲线

由图6～图8可知，钢球最大速度位于与内圈、内凸缘接触区，最大速度及位置随着钢球的转动而不断变化，在不同时刻于内、外列钢球间变换，并未集中位于某一列钢球。保持架的最大速度位于保持架的外边缘，最大速度及位置也随保持架的转动而不断变化，在不同时刻于内、外列保持架间变换。

3.2.2 仿真验证

由轮毂轴承内部运动学关系，假设钢球与内、外凸缘的沟道之间为纯滚动。当内凸缘转动、外凸缘固定时，钢球公转速度(即保持架速度)Vc、钢球与内凸缘接触点速度Vi可表示为[8]

(3)

(4)

式中：Ni为内凸缘转速；Ne为外凸缘转速；Dw为钢球直径；Dpw为球组节圆直径；α为轮毂轴承接触角。有限元分析与解析解结果对比见表5,误差在3%以内，符合要求。

表5 有限元结果与解析解对比

3.3 应力分析

轮毂轴承在30 ms时的等效应力云图如图9所示，钢球应力最大值位于钢球与内凸缘接触部位，为532.50 MPa。

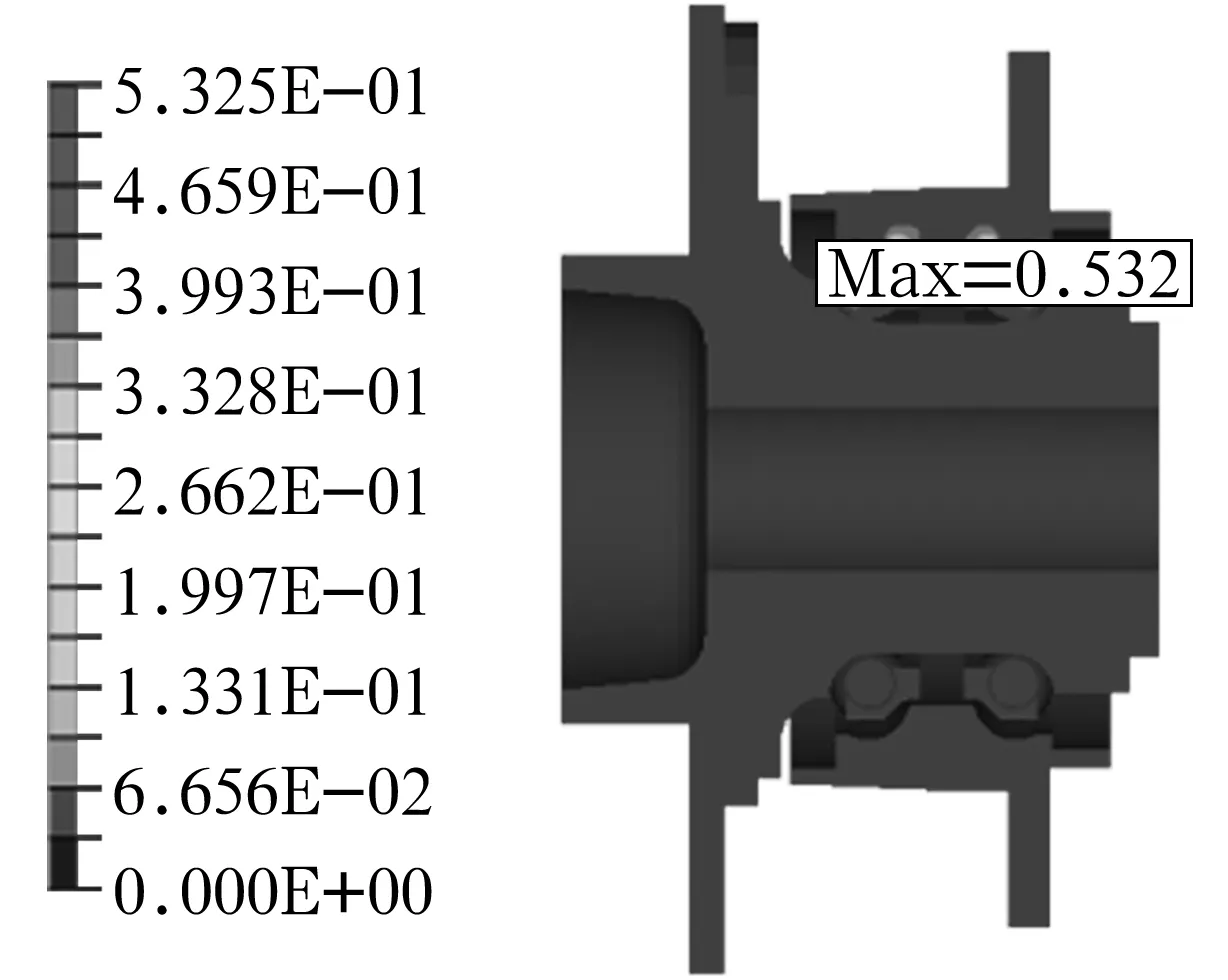
图9 轮毂轴承等效应力云图

钢球分别在8,25.5,30 ms时的等效应力云图以及30 ms时的钢球切片云图如图10所示。由图可知，应力集中位于钢球与内、外凸缘以及内圈接触区域;另外，由图10d可知，最大应力位于钢球外表面以下某一深度的区域，向外逐渐衰减，扩展至接触表面。由此可知，轮毂轴承显式动力学仿真结果与Hertz理论结果一致[9]。

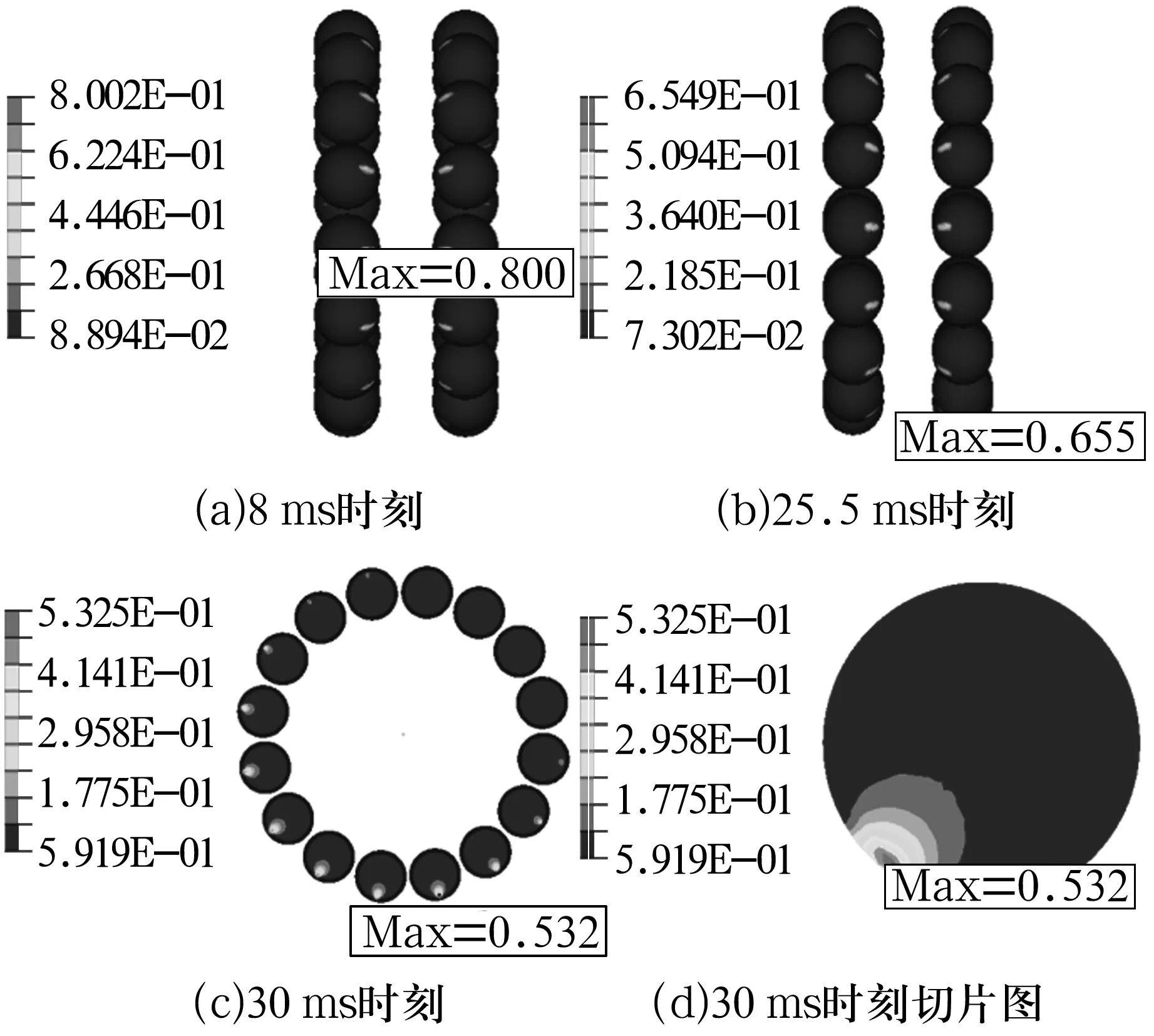
图10 双列钢球应力云图

内、外列钢球最大等效应力时程曲线如图11所示。内、外列钢球最大等效应力值近似呈周期性变化，周期约为16 ms。任一时刻内、外列钢球应力值均存在微小差异。

由图10～图11可知，轮毂轴承最大应力位于钢球与凸缘接触区，在整个运转周期内，最大应力值及位置在内、外列钢球上交替变化，并未集中位于某一列钢球。

图11 双列钢球应力时程曲线

3.4 加速度分析

钢球与内圈、内凸缘接触点以及保持架外边缘节点的y向(径向)加速度时程曲线如图12所示，采样时间为0.5 ms。钢球加速度远大于保持架的加速度(接近为0)，轮毂轴承在运转过程中保持架振动较微弱，基本处于平稳运转的状态。外列钢球加速度曲线存在较小波动，表明外列钢球存在微小的径向振动，加速度最大值为5.3×104m/s2。与外列钢球相比，内列钢球加速度曲线波动较为明显，但并未出现较大峰值，最大值为1.8×105m/s2，属于正常情况下的无缺陷轮毂轴承振动，钢球无规则的微小振动表现了轮毂轴承在转动过程中呈现出强烈的非线性。

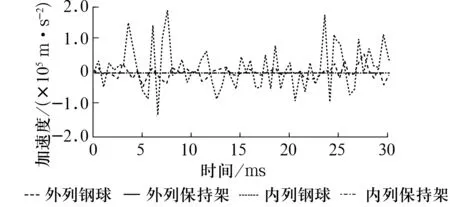
图12 节点加速度时程曲线

4 相同载荷不同车速动态特性分析

研究汽车处于满载条件下，分别以低、中、高速状态行驶，车速分别达到40,80和120 km/h时的轮毂轴承动态特性。

选取钢球与内凸缘接触位置的相同节点，车速分别为40,80和120 km/h情况下节点的应力时程曲线如图13所示。随车速增大，相同的时间历程内应力峰值出现次数逐渐增加。30 ms内车速在40，80，120 km/h时出现的应力峰次数分别为3，5，6次。车速为40,80 km/h时，应力峰值不大，较为稳定；车速达到120 km/h时,应力峰值明显大于中低速时的应力峰值。汽车高速行驶时轮毂轴承转速较高，钢球产生了较大的离心力，对接触应力有较大影响；车速较低时，轮毂轴承转速较低，离心力小，对接触应力影响较小。

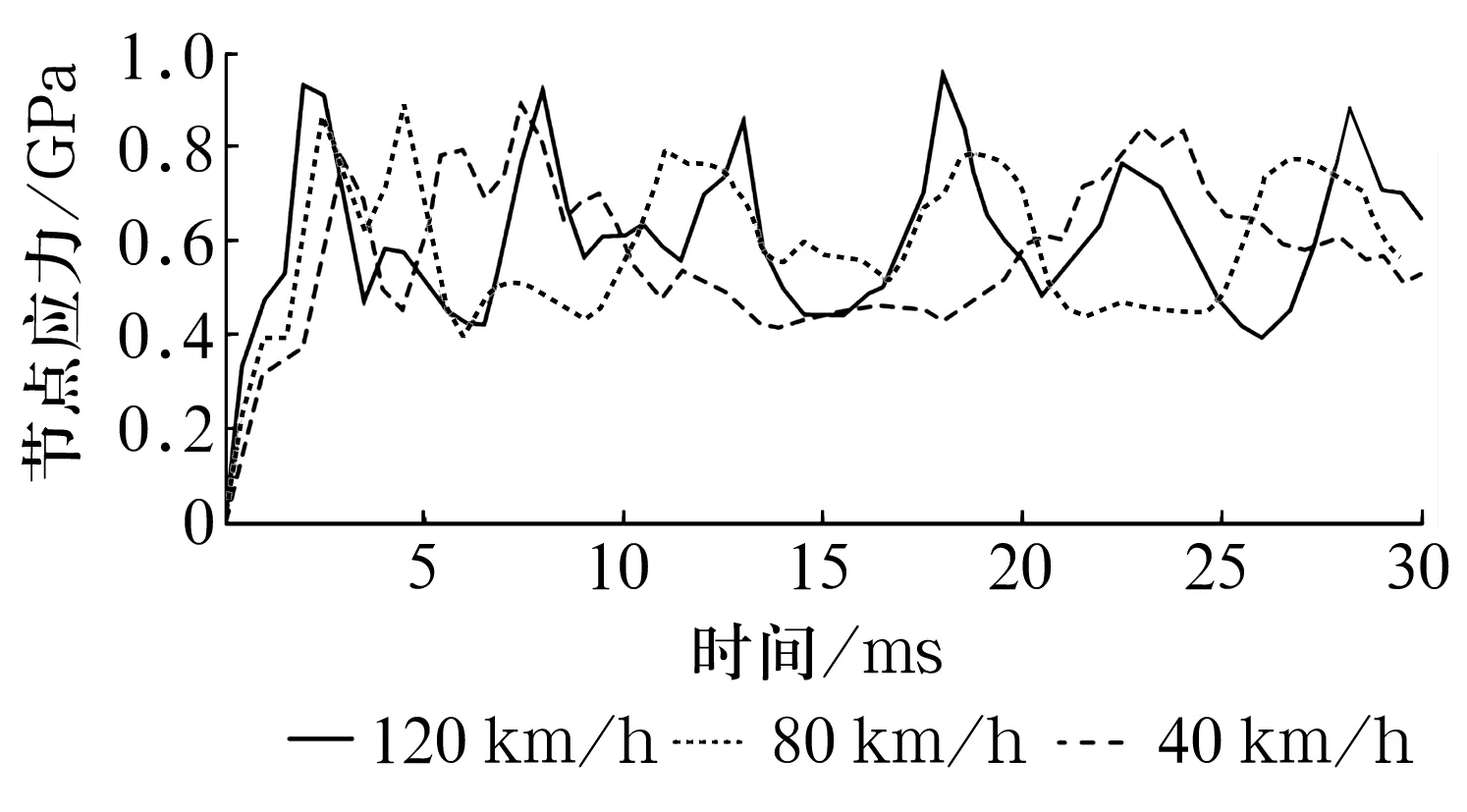
图13 接触节点应力时程曲线

车速分别达到40,80和120 km/h下的加速度时程曲线如图14所示，采样时间为0.5 ms。当车速分别为40和80 km/h时，节点加速度曲线波动较大，出现较大的加速度峰值；当车速达到120 km/h，节点加速度曲线波动较小且并未出现较大峰值，变化平稳。高速转动时钢球的加速度较中低速时更小，反映了车速较高时轮毂轴承振动较小，运转更加平稳。

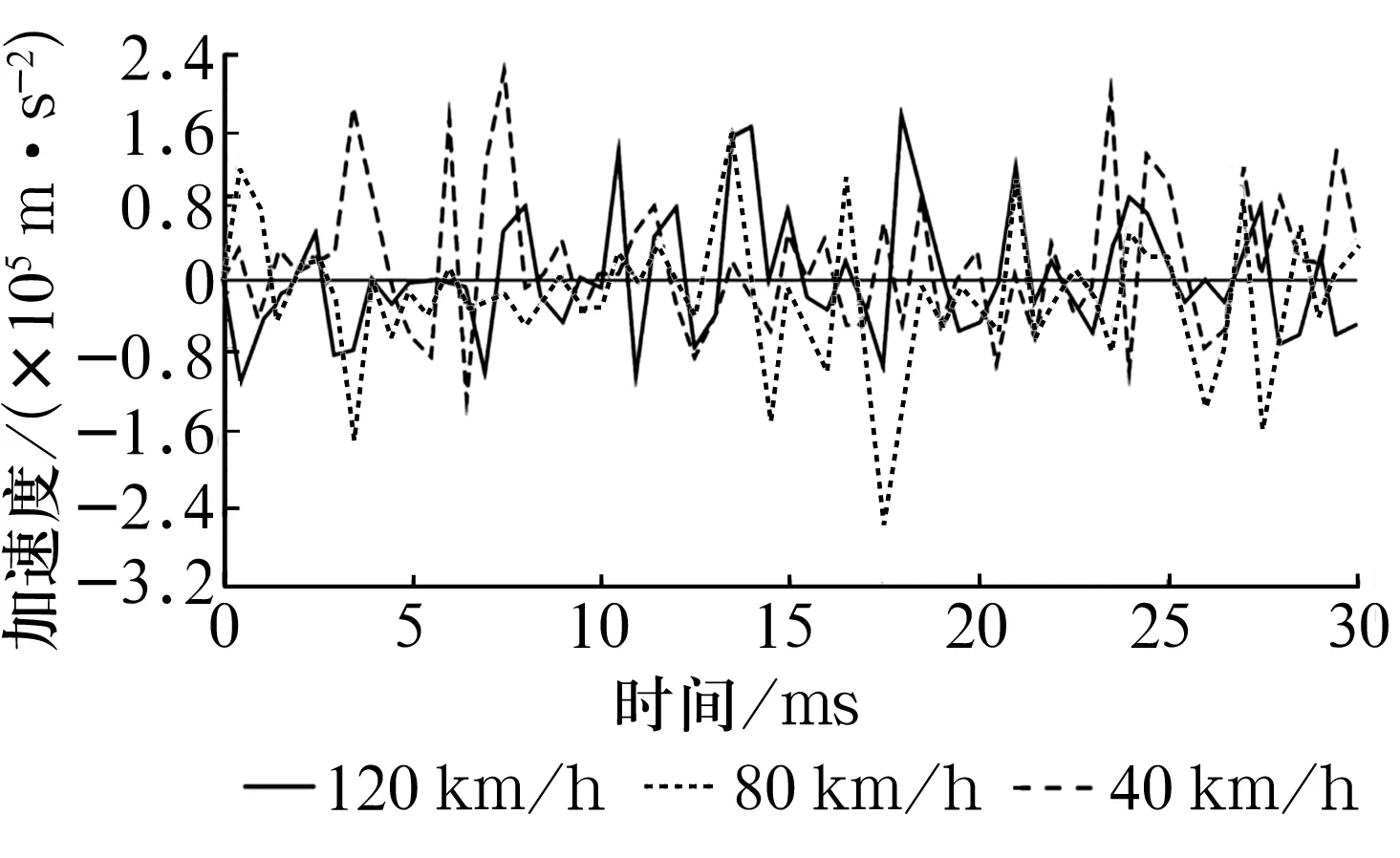
图14 接触节点加速度时程曲线

5 结论

1)应力集中位于双列钢球与内、外凸缘以及内圈的接触区域。应力最大值出现在钢球接触表面以下一定深度区域，并逐渐向外衰减，扩展至外表面。

2)钢球的最大应力、速度及位置随着钢球的转动，在2列钢球上交替变化；内列钢球加速度峰值约为外列钢球加速度峰值的3.4倍，内列钢球振动较为强烈。

3)相同的时间历程内，高速条件下钢球应力峰值出现的次数与数值均大于中低速时。高速转动时钢球的加速度较中低速时更小，反映了车速较高时轮毂轴承振动较小，运转更加平稳。