基于多元线性回归模型PM 2.5预测问题的研究

张玉丽,何　玉,朱家明

(1.安徽财经大学　金融学院，安徽　蚌埠　233000；2.安徽财经大学　统计与应用数学学院， 安徽　蚌埠　233000)



基于多元线性回归模型PM 2.5预测问题的研究

张玉丽1,何玉1,朱家明2

(1.安徽财经大学金融学院，安徽蚌埠233000；2.安徽财经大学统计与应用数学学院， 安徽蚌埠233000)

摘要：针对PM 2.5的预测，使用相关系数，主成分分析，牛顿插值法等方法，利用SPSS，EVIEWS等软件，建立PM 2.5预测的多元线性预测模型，并对模型的结果进行残差分析以及K-S检验，得到了较为理想的结果，最后，结合所得结果为当地政府提出了建议。

关键词：PM 2.5；K-S检验；主成分分析；多元线性回归模型；EVIEWS

改革开放带来了经济的空前发展，加入世贸组织使我国的经济发展水平更上一个台阶，但持续高速的经济增长速度带来了严重的污染问题。比如南京出现的玫瑰红雾霾等均反映了环境处于恶化的边缘。PM 2.5预测的方法较多，张怡文(2015)使用神经网络模型对PM 2.5的浓度进行预测，该方法经度较高，但是对样本数据集的要求过高，实际应用价值不高[1]。彭斯俊对PM 2.5的时间序列使用ARIMA模型进行预测，但该预测方法随着时间的延长误差逐渐增大[2]。PM 2.5预测指标一般选取容易获得的包括PM 10、O3、CO、 SO2、NO2以及温度等指标[1-3]。PM 2.5浓度的计算多采用物理的方法，由于其自身的特点导致普通的物理方法精度难以满足要求，精确地计算方法成本较高，而PM 10,O3等指标的测量技术较为成熟，利用影响空气质量的指标之间的相关关系，在提高PM 2.5预测精度的同时可以降低PM 2.5的测量成本。通过对PM 2.5环境指标的预测，提高市民工作、生活的效率，加强呼吸道健康、行车安全等方面的保障具有极其重要的意义。

1数据的获取及假设

本文所使用的数据来自于上海检测中心官网以及中国环境质量在线监测分析平台。选取的指标包括日均PM 2.5浓度值，日均PM 10浓度值,臭氧日均一小时的平均浓度值、臭氧日均8小时平均浓度值、日均CO浓度值、日均SO2浓度值、日均NO2浓度值以及每日平均温度。共选取从2015年1月1日到2015年5月31日共151组数据。为方便解决问题，做出以下几条假设：(1)影响PM 2.5浓度的指标包含本文所列指标，其他指标的影响忽略不计；(2)假设当地不同污染物的浓度是均匀的，相邻地区不存在较大的差异；(3)不考虑天气的原因对自然物浓度的影响；(4)所搜集的数据来源可靠，忽略人为误差的存在。

2数据的处理

2.1数据的补全

由于所搜集数据不完整，为保证模型的完整性，使用牛顿插值法进行数据的补全。其步骤如下[4]：

(1)输入n值及(xi,f(xi)),i=0,1,……,n；要计算的函数点。

(2)对给定的x,由

Nn(x)=f(x0)+(x-x0)f[x0,x1]+(x-x0)(x-x1)f[x0,x1,x2]+…+(x-x0)

(x-x1)…(x-xn-1)f[x0,x1,…,xn]

(3)计算Nn(x)的值。

(4)输出Nn(x)

2.2数据的无量纲化

由于自然环境的复杂，环境数据之间存在不同的量纲，为更好的刻画数据之间的非线性关系，使用牛顿插值法插入4组数据后对补全的数据取自然对数，并对其进行无量纲化处理[5]，方法如下：

(1)

其中，i为年份，j为指标序号，xij为第个指标的第年的数据，min(xj)为第j个指标的最小值，max(xj)为第j个指标的最大值。

3主成分分析法

3.1模型的准备

回归模型的建立要求变量之间相关性较低，否则多重共线性的存在会影响模型的准确性，采用线性相关系数研究各指标之间的线性相关性。

(2)

使用EVIEWS软件得到了影响PM 2.5浓度的各指标数据之间的相关系数矩阵见表1。

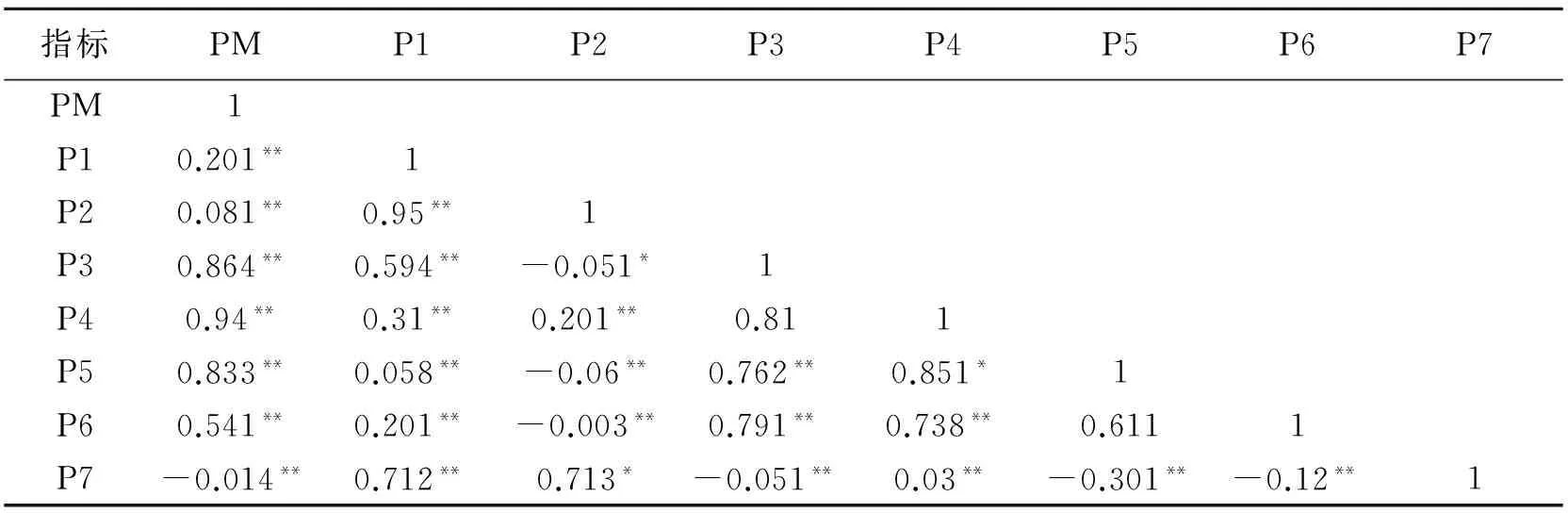
表1　影响PM 2.5各指标相关系数矩阵

注：**表示在0.01的水平上显著，*表示在0.05的水平上显著。指标PM表示PM 2.5；P1表示PM 10；P2表示臭氧日均一小时的平均浓度值；P3表示臭氧日均8小时平均浓度值；P4表示CO；P5表示SO2；P6表示NO2；P1表示温度的数据。

从各变量之间的相关系数值可以看出，所选取的变量与PM 2.5之间相关性较强，其中CO,SO2，NO2与PM 2.5相关性最为明显。而这些气体的产生主要来源于汽车尾气以及工厂废气的排放。由于变量之间存在着较强的相关性。难以直接进行回归，因此适合采用主成分分析法进行数据的降维[8]。

3.2模型的建立与求解

我们使用SPSS软件对所得数据进行分析，所得主成分的贡献率结果见表2：

表2　主成分贡献率

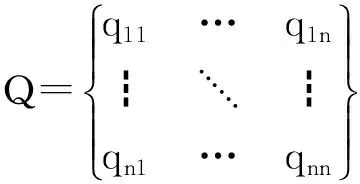
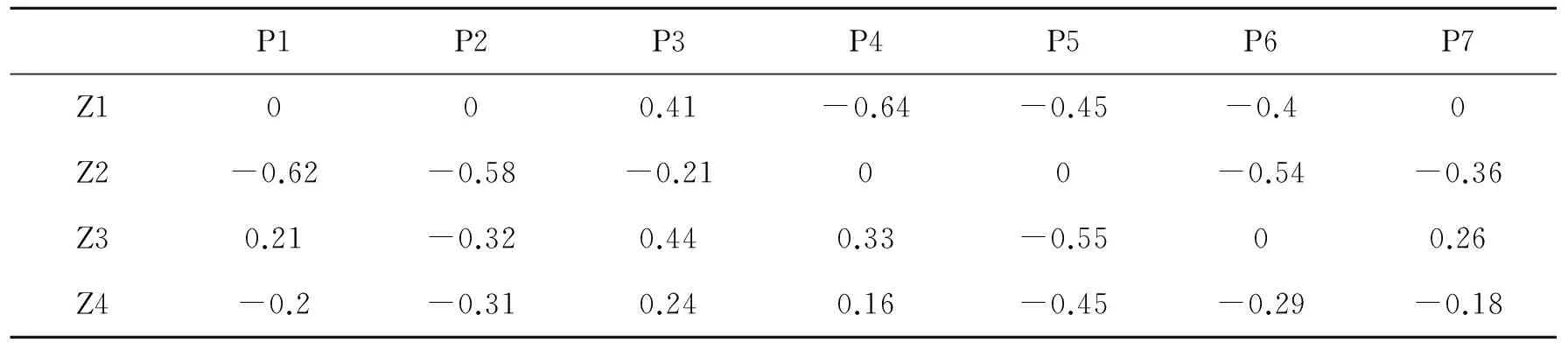
表3　观测指标在主成分中的比重

4多元线性回归模型

4.1模型的准备

考虑到污染分布问题的复杂性，影响PM 2.5的变量之间的关系存在较强的非线性关系。采用幂函数的形式进行多元线性回归[7-8]。

(3)

为了便于求解，我们对等式(3)两边同时取自然对数：

lnY=a0+a1ln X1+a2X2…akXk

(4)

4.2模型的求解

结合(3),使用EVIEWS软件对数据进行回归分析，并结合主成分分析结果得到以下的预测模型：

(5)

因此该日的PM 2.5浓度预测值为：

(6)

5模型的检验

5.1残差分析

多元线性回归模型要求残差应具有正态性。为进一步检验本文所建立的预测模型的可靠性，对其残差是否服从正态分布进行检验。对于残差数列，假设它是正态总体的一个样本，该正态分布总体为N(u,δ2)，其中均值和方差未知，因此，将采用极大似然法估计得到正态分布的参数[9]。

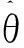
(7)

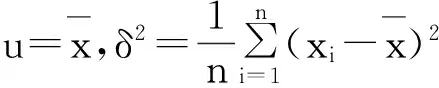
将所求得到的残差的数据ε1，ε2,…,εk代入得到u=0.03547，δ2=0.18202，使用EVIEWS做出该估计所得正态分布概率密度曲线，如图1所示。

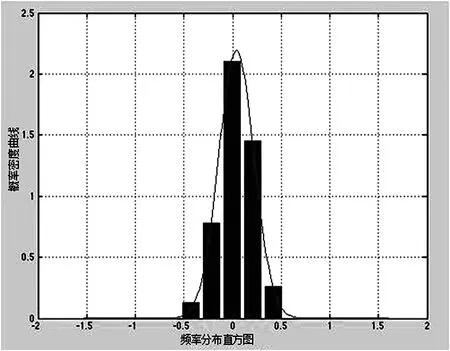
图1　残差频率分布直方图

5.2K-S检验

对于极大似然法所得结果，需要对残差数列进行进一步检验，判断其是否满足的正态分布，使用Kolmogorov-Smirnov 检验[10]，即K-S检验判断残差的样本数列是否服从正态分布，通过比较经验分布函数和理论分布函数的差异检验，检验二者是否服从某种分布。首先，定义检验统计量为：

D=max|Fn(x)-F0(x)|

(8)

当实际的D>D(n,a)(其中n为样本容量，a为显著性水平，D(n,a)为临界值)则拒绝原假设，否则接受原假设。

对于残差数列，使用SPSS软件进行K-S检验结果见表4。

表4　K-S检验结果

做出经验分布和理论分布的函数对比的图像，如图2所示。

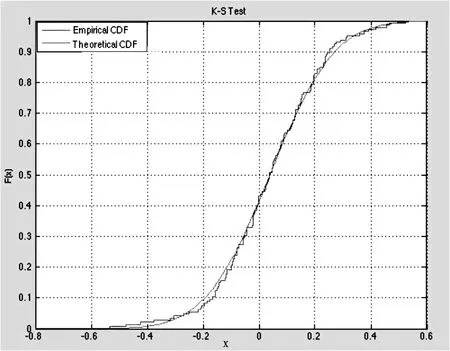
图2　理论和经验分布函数图像

从K-S检验的结果可以看出，应该接受原假设，因此该数据序列可以看成是服从，的正态分布，同时从经验分布函数和极大似然估计的正态分布函数图像可以看出，二者之间差异较小，估计误差可以忽略。

5.3预测结果检验

为了保证所建模型的准确性，对模型的预测结果进行交叉检验，原理如下：

k 阶交叉验证是通过将样本总体分为k 个子样本，选择其中一个子样本作为验证数据，其他数据用于训练。重复验证k次，并根据k次的运行结果最终得到单一的估测值。通过使用3阶交叉验证对预测结果进行检验[11]。检验结果见表5。

表5　交叉检验结果

做出了真实值与预测值的折线图的比较的图像，如图3所示。

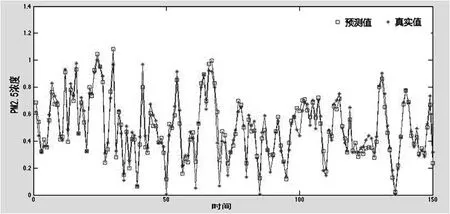
图3　真实值与预测值的比较

从调整后的可决系数可以看出，表明解释变量能够对被解释变量进行很好的解释。从模型预测结果可以看出，预测值和真实值之间的差距较小，预测结果较为理想。

6结束语

本文通过影响环境质量的各项指标对PM 2.5的值进行预测。通过相关性分析得到指标之间的相关性较高的结论。在进行主成分分析的基础上建立多元线性回归模型。模型拟合优度较高，通过K-S检验。残差分析等得到所得预测模型合理的结论。同时本文还得到当前上海市的CO,SO2，NO2等气体污染物对上海市的污染影响较大，而这些气体主要是由汽车尾气以及工厂排放导致，因此建议上海市政府采取相应的措施，大力发展公共交通，降低汽车尾气的排放量，严格监督工厂的废气排放，促进当地经济和环境的协调发展。

参考文献：

[1]张怡文，胡静宜，王冉．基于神经网络的PM(2.5)预测模型[J]．江苏师范大学学报:自然科学版，2015，32(1)：63-65．

[2]彭斯俊，沈加超，朱雪．基于ARIMA模型的PM(2.5)预测[J]．安全与环境工程，2014(6)：125-128．

[3]陈强，梅琨，朱慧敏，等．郑州市PM(2.5)浓度时空分布特征及预测模型研究[J]．中国环境监测，2015，31(3)：105-112．

[4]唐晖．传感器网络数据规范与插值方法研究[D]．长沙：湖南大学，2010．

[5]郭亚军，易平涛．线性无量纲化方法的性质分析[J]．统计研究，2008，25(2)：93-100．

[6]朱家明，王犁，童金萍，等．我国就业人数的主要影响因素分析及前景预测[J]．数学的实践与认识，2010，40(15)：57-70．

[7]荆涛,李霖,于文柱，等.t分布受控遗传算法优化BP神经网络的PM 2.5质量浓度预测[J].中国环境监测,2015(4):100-105．

[8]胡玉筱，段显明．基于高斯烟羽和多元线性回归模型的PM_(2.5)扩散和预测研究[J]．干旱区资源与环境，2015，29(6)：86-92．

[9]伊丽米热·阿布达力木，迪丽努尔·塔力甫,阿布力孜·伊米提,等.乌鲁木齐市大气可吸入颗粒物浓度与气象因素的相关性研究[J]．新疆大学学报:自然科学版，2012，29(01)：94-99．

[10]邓启红，黄柏良，唐猛，等．长沙市大气颗粒物PM(10)质量浓度的统计分布特性[J]．中南大学学报:自然科学版，2012，43(4)：1567-1573．

[11]孙迎雪，吴光学，胡洪营，等．基于达标保证率的昆明市污水处理厂出水水质评价[J]．中国环境科学，2013，33(6)：1113-1119．

(责任编辑：马世堂)

收稿日期：2016-01-20

基金项目：安徽省大学生创新项目(201510378470);国家自然科学基金(11301001); 安徽财经大学教研项目(acjyzd201429)。

作者简介：张玉丽(1992-)，女，安徽省利辛县人，在读本科生，主要从事应用数学与数学建模研究。*通讯作者：朱家明，副教授，E-mail:zhujm1973@163.com。

中图分类号：TP391.6

文献标识码：A

文章编号：1673-8772(2016)03-0092-06

Study of the Prediction of PM 2.5 Based on the Multivariate Linear Regression Model

ZHANG Yu-li1,HE Yu1，ZHU Jia-ming2

(1. School of Finance, Anhui University of Finance & Economics, Bengbu 233000, China;2. School of Statistics and Applied Mathematics， Anhui University of Finance & Economics, Bengbu 233000,China)

Abstract：For PM 2.5 predictions, we use the correlation coefficient, principal component analysis, Newton interpolation and other methods, and then use SPSS, EVIEWS software. We test them by using residual analysis and K-S test to obtain a more satisfactory result. Finally, we put forward a proposal for local government in line with the results.

Key words:PM 2.5; K-S test; Principal component analysis; Multivariate linear regression model; EVIEWS