基于半参数法的中国跨地区全要素生产率研究
张倩肖,李丹丹(西安交通大学 经济与金融学院,陕西 西安 710061)
区域发展
基于半参数法的中国跨地区全要素生产率研究
张倩肖,李丹丹
(西安交通大学 经济与金融学院,陕西 西安 710061)
摘要:文章利用2002-2014年中国工业企业水平的微观数据,采用Levinsohn and Pertrin法(简称LP半参数法)系统分析和测算中国31个省份全要素生产率(TFP)的变动情况,同时比较跨地区生产率差异并分析其差异原因。结果表明,中国跨地区全要素生产率具有较大差异,其中环渤海和东南地区及中部地区的TFP均值相对较高,其次是东北地区,西南和西北地区TFP均值最低。因此,要改善中国不同地区的全要素生产率差异,政府需要在全面实施创新驱动发展战略、完善产业政策、优化资源配置和降低地区边界效应等方面做出努力。
关键词:全要素生产率;LP半参数法;地区差异
[DOI]10.3969/j.issn.1007-5097.2016.03.008
一、引 言
中国自改革开放以来经济得到了飞速的发展,但是不同区域和地区间经济发展的非一致性却日益突出。在20世纪90年代以前,人们认为地区经济差异的重要原因是要素投入不同造成的。有关重要素投入的理论和研究不断出现,其中Basu,Susanto and John(1997)[1]的文献是早期最先关注不同国家经济差异的经典之作。但是,在90年代的中后期,学者们对重要素投入的观点提出质疑,尤其是对新古典理论中的资本报酬递减的质疑。Easterly(2001)[2]研究认为,如果一个地区经济发展比较落后,那么该地区所投入的资本要素必然会小于经济发达地区所投入的资本要素,而资本的报酬增长速度必然会高于经济发达地区的,因此资本就会从经济比较发达的地区流向经济落后的地区,所以一个地区经济落后的真正原因并不是由于资本的匮乏导致的。在随后的研究中,一些学者考察了人力资本对经济绩效的作用。研究认为,虽然人力资本对经济增长有着重要的作用,但是它对不同国家经济效率的差异解释不到1/3,对经济增长的贡献率比较低,因此,人力资本并不是解释国家或地区经济差异的重要原因(Ra⁃phael,2015)[3]。基于以上分析,学者们基本得出一致结论认为,经济增长实际上是由许多因素共同发挥作用的,在市场经济体制下,经济绩效的提高实际上就表现为全要素生产率(简称TFP)对经济绩效的影响。因此可以说,国家或地区贫富的差异是来源于生产率的差异。
大多数文献研究全要素生产率时,主要研究的是农业和制造业部门,而针对工业的研究比较少。工业在中国经济发展和增长过程中起着举足轻重的作用。伴随着各国经济发展条件的差异以及国际产业的分工,未来中国工业的增长将会在世界经济的发展中扮演着更加重要的角色。对于总体TFP的研究已有文献大都主要是从宏观层面出发,要么采用传统的索罗余值法,要么采用数据包络法(DEA)和随机边界法(SFA),从企业层面基于半参数法研究TFP的文献屈指可数。值得注意的是,由于企业的技术水平在某种程度上是可以事前认知的,企业根据已知的技术水平再选择合适的要素投入水平,因此用传统宏观研究方法测量企业生产率会出现同步偏差问题和选择偏差问题,使得估计结果不准确,所以传统方法并不适用于微观企业全要素生产率研究。针对以上问题,一系列的最新修正方案被提出,并形成了很多前沿的估计方法,目前国际上流行的是 Olley and Pakes法(简称 OP法)和Levinsohn and Pertrin法(简称LP法)。半参数法主要是一并建立了参数关系和非参数关系,但并非是参数和非参数模型的简单叠加,而是两种方法的有机结合,能够有效解决生产函数的同步偏差问题和选择偏差问题。
二、文献综述
改革开放后,国内外的学者们对中国全要素生产率相继进行了研究,但是对全要素生产率的估算结果存在非常大的差异,这就引发了许多争论。究其原因,主要包括两点:第一是样本数据的来源与处理方法的不一致,第二是全要素生产率的测算方法不一致。目前测算全要素生产率的方法有很多,大致可分为三类:①参数法,这类方法事先需要假设具体的生产函数再进行测算,主要包括索罗余值法和随机前言生产函数法;②非参数法,这类方法不需要设定先验的生产函数,是通过获得样本点的观测数据后直接利用线性优化给出距离函数和边界生产函数进行估算,主要包括Malmquist生产率指数法和数据包络分析(DEA)等;③半参数法,主要包括Olley and Pakes[4]法(简称OP法)和Levinsohn and Pertrin[5]法(简称LP法)。半参数法主要是一并建立了参数关系和非参数关系,参数关系是针对影响产出的主要因素建立的,而非参数关系则是针对其他影响产出的未知因素建立的,并在生产函数中一起加以估计,这样就能够有效解决生产函数的样本选择和内生性问题。每一种方法都有各自的适用对象和优缺点,那么究竟哪种方法更为恰当和更为使用呢?为此,本节将对有关全要素生产率的测度方法的文献进行梳理和述评。
索洛余项度量的是经济增长中要素投入所不能解释的部分,指企业实际观察产值和由最小二乘法计算所得的估计产值之间的差额。由于模型简单,合乎经济原理,因此很多学者利用这种方法对中国全要素生产率进行测算,如李平等(2013)[6]测算了中国总体和省级生产率变化及其对经济增长的贡献率;杨茜淋(2013)[7]对中国工业分行业全要素生产率进行估计;张建升(2011)[8]对中国省域全要素生产率地区差异的动态演进进行研究等。索洛余值法开创了经济增长源泉分析的先河,是新古典增长理论的一个重要贡献。用索洛余值法计算全要素生产率的优点是思路清晰,算法简单,很容易理解。缺点是它的必要条件是需要估算出∂和 β的参数值,这就需要对技术水平A做出一定的假设。假设1:技术水平A是一个固定的常数A=A0;假设2:技术水平A是关于时间t的指数函数,即A=A0eλt;假设3:技术水平A是关于时间t的指数增长A=A0(1+γ)t。但是,以上几种假设都很难令人信服。因为,技术水平的提高是由很多已知与未知因素共同导致的结果,它既不是一个常数也不是简单的关于t的指数函数,应该是一种难以确定的非线性函数。随机前沿生产函数法测度全要素生产率的步骤主要是首先设定前沿生产函数,然后估计前沿生产函数中的参数。如蒲勇健等(2014)[9]基于随机前沿超越对数生产函数对中国再生资源产业的技术效率及影响因素进行研究;余泳泽等(2012)[10]利用该方法对中国高技术产业地区效率差异与全要素生产率增长率分解进行研究等。但是该方法也存在一些不足,如参数太多,且该函数中的一些二次项无法从经济学角度给出合理解释;假设各年度的参数相同,否定了不同时间经济发展的多样性[11]。随机前沿生产函数法在计算全要素生产率的优势是:①通过估计生产函数能对个体企业的生产过程进行描述,从而有效地控制了对技术效率的估计;②相比于其他方法,该方法的模型可以较好地处理测度误差,并考虑到了随机误差对经济增长的影响,因此能较好地模拟现实经济发展的状况。随机前沿生产函数法的劣势主要是:这种方法在具体的研究过程中假设条件太多,这样就使得该研究的应用受到了较大的限制。
测度全要素生产率的非参数法也越来越多地被应用到生产率研究的领域中。如孙庆兰(2013)[12]利用该方法对流通业与制造业全要素生产率的交叉作用进行了实证研究;石腾超等(2014)[13]基于DEA分解的Malmquist指数法对中国制造业全要素生产率区域差异及其原因进行研究;孙晓华等(2012)[14]分别采用ATFP法、LP法和DEA-Malmquist指数法对中国制造业15个子行业的全要素生产率进行了测算及比较。用非参数法计算全要素生产率的优点是,它们不需要事先设定具体的生产函数,而是通过获得样本点的观测数据后直接利用线性优化给出距离函数和边界生产函数进行估算,并且可以将全要素生产率具体分解为技术进步、规模效应和配置效率。非参数法的缺点是,数据包络法(DEA)和Malmquist指数法都没有考虑到样本的随机因素,这就会造成很大的测量误差。
通过对有关文献的梳理和述评可以看出,随着微观企业统计数据可获得性的逐渐增强,有关中国全要素生产率的总体研究趋势正在由宏观走向微观。但是,传统测量微观企业全要素生产率的估计方法会产生两个问题,即联立性问题与样本选择问题,也就是通常所说的内生性问题。联立性问题是指在位企业在做要素投入的决策之前,会在某一个时刻感觉到一部分的生产率,因此这就会影响企业做出要素投入的决策;样本选择问题是指由于市场竞争和企业利益最大化,生产率较低的企业会被市场淘汰,而留在市场中的在位企业都是生产率相对较高的企业,因此如果在估计企业的生产率水平时只用在位企业的样本来估计,会使得企业的生产率水平得到过高的估算,因此估算结果会不客观和不准确。为了解决这些问题,目前较为合适的是采用半参数法。然而目前采用半参数法来测度企业全要素生产率的文献比较少。张杰等(2009)[15]以中国1999-2003年之间的全部国有与规模以上的非国有企业的统计数据为样本,采用OP半参数法估计了企业的全要素生产率。余淼杰(2010)[16]同样使用类似的方法和数据估计了全要素生产率。基于此,本文将详细介绍和阐述半参数法。半参数法包括Olley and Pakes法(简称OP法)和Levinsohn and Pertrin法(简称LP法)。半参数法主要是一并建立了参数关系和非参数关系,参数关系是针对影响产出的主要因素建立的,而非参数关系则是针对其他影响产出的未知因素建立的,并在生产函数中一起加以估计,这样就能够有效解决生产函数的样本选择和内生性问题。
(一)Olley and Pakes法(简称OP法)
根据柯布—道格拉斯生产数可以得到以下关系:

其中,yit、kit、和lit分别表示的是企业增加值、资本投入和劳动投入的自然对数形式;ωit表示的是企业不能被观测到的且随着时间变化的异质性生产率,它代表了企业的技术、管理水平等因素;εit表示的是真正的误差项,或者说是生产率偏离预期的冲击。ωit和εit都不可能被观测到,其区别就在于,企业在观测到本期的生产率水平ωit后,会决定资本和劳动的投入量,因此,ωit与要素投入有关,而企业在做出决策之前不能观测到εit,因此εit与要素投入不相关。
Olley and Pakes假定生产率的变化服从一阶马尔科夫过程,用公式表示为,其中,Jit表示的是第t时期的全部信息。这就意味着企业下一时期的生产率只与当期的生产率有关。Olley and Pakes假设资本按照永续盘存法形成,即,其中,δ表示折旧率,it-1表示t-1时期的投资。由资本积累的方程可以知道,在t时期的资本投入完全是由上一时期的全部信息集合决定的,因而投资与当期的生产力水平ωit和随机扰动项εit都不相关。因此,在上式的生产函数中,只有lit是内生变量。
在多时期的不确定动态环境中,由于企业的目标是保证未来预期利润贴现加总达到最大化,因此,企业的投资决策变量是关于生产率和资本的函数,即iit=it(kit,ωit)。Olley and Pakes假设该过程中仅存在生产率这一个不可观测的变量,因此在资本kit给定的情形下可求出生产率ωit关于投资iit的函数即:ωit=ht(kit,iit),将该生产率的表达式带入方程(1)可得:
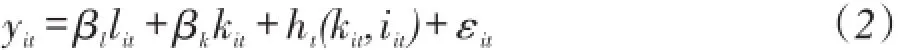
同时,定义φt=βtkit+ht(kt,it),将其带入方程(2)可得:

运用序列估计(Paquet,2001)[17]方法进行估计可得到φt的估计值φt劳动的系数估计值 βl。由于在该过程中已经用关于投资和资本的函数φt将生产率显性地表示出来,因此在方程(3)式中不存在内生性问题。
接下来估计资本的系数 βk。对于任意给定的βk,由和的表达式以计算出企业的全要素生产率,即ωit=βtkit-φt。又因为假设生产率服从一阶马尔科夫过程,因此t时期的生产率可以写成t-1时期生产率和信息值(innovation)的和,用公式表示为:
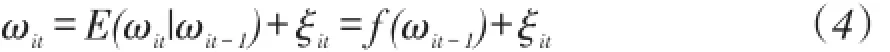
其中,f(ωit-1)表达的是关于 ωit-1的函数,ξit表达的是t-1时期和t时期之间的信息值,它与t-1时期的信息集不相关。又因为t时期的资本完全是由t-1时期的全部信息集合决定,因此它与ξit也不相关。将方程(3)可以改写为:
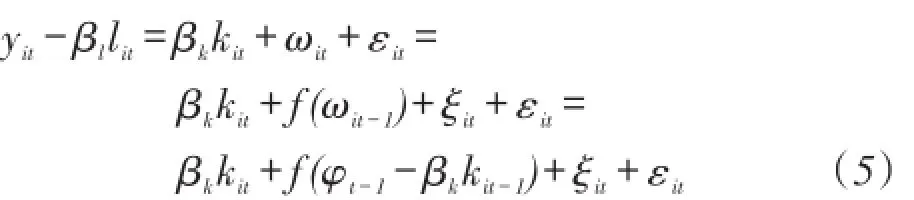
由于假定kit与εit、ξit都不相关,因此在方程(5)中通过将内生变量lit移动到方程的左边,该方程不包含任何内生变量。然后采用非线性最小二乘法就可以估计出资本的系数βk的估计值 β∧k,这样生产函数中的所有系数都估计出来了,最后通过索罗残值法就能得到企业的全要素生产率。
(二)Levinsohn and Pertrin法(简称LP法)
Levinsohn and Pertrin则认为,由于调整成本的存在,投资会因为受到调整成本的影响而不能灵活地反映企业生产率的变动情况,因此上述OP方法不能完全解决回归项和残差项之间的内生性问题。LP方法则建议采用中间投入变量作为代理变量。因为企业只要进行生产,就会使用中间投入品,而且中间投入品的调整相对于投资来说更加灵活,因此更能完全反映企业生产率的变动情况。在对柯布-道格拉斯生产函数取自然对数后可得:

其中,yit和mit分别表示取自然对数后的企业产出值和中间投入品。与OP方法所假设的投资与生产率存在单调关系不同,LP法假定在kit给定的条件下,mit是关于ωit的单调增函数,即mit=mt(kit,ωit)。对其求反函数可得:,这意味着生产率是关于资本和中间投入品的函数,将其带入方程(6)中可得:

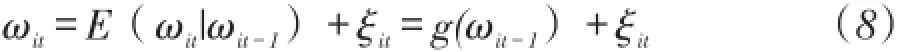
其中,g(ωit-1)表示的是关于ωit-1的函数,ξit表达的是t-1时期和t时期之间的信息值,它与t-1时期的信息集不相关的,因此kit和εit、ξit都不相关,这可以当作为识别的一个矩条件。由方程(6)、(7)和(8)可得:
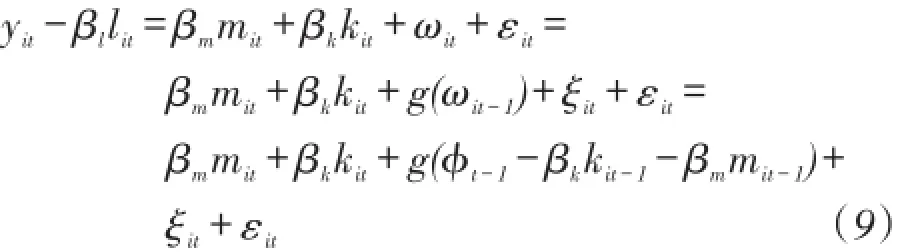
由于中间投入品mit作为企业在t时期的决策变量虽然与误差项εit不相关,但是却和信息值ξit相关,因此可以用其滞后一期值mit-1当做mit的工具变量。然后用ϕt-1-βkkit-1-βmmit-1多项式表示g(ϕt-1-βkkit-1-βmmit-1),根据矩条件,使用GMM方法就可以估计出βk和βm,最后通过索罗残值法求得全要素生产率:

两种半参数法都可以很好地消除内生性的问题,但是由于OP方法中的一个假定是要求代理变量(投资)和总产出始终保持单调递增关系,这就表示那些投资额为零的样本企业并不能够被估计。实际上,并非每一个企业在每一年的投资都为正,如果采用OP法来估计企业的全要素生产率就会丢弃掉很多企业样本。LP法是以中间投入指标代替投资额作为代理变量,从数据的角度出发,这样所损失的样本量将比OP方法小很多,在数据的筛选过程中比较有效,从而估计结果更加精确。通过这两种方法的对比,本文将采用LP法来测度我国2002-2014年全部国有和规模以上非国有的工业企业层面的全要素生产率。
三、基于LP半参数法全要素生产率的测度
(一)模型和变量的界定
本文借鉴Levinsohn and Pertrin(2003)的模型方法,模型设定为如下形式:
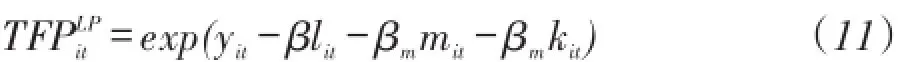
在(11)式中,yit表示企业实际产出值(对数),lit、mit和kit分别表示劳动投入、中间投入和资本投入(对数)。劳动投入变量用从业人员平均人数来表示,资本投入变量按照永续盘存法即kt=(1-δ)kt-1+it-1,其中,δ表示折旧率,it-1表示t-1时期的投资,ki为第t年的实际资本存量,kt-1为第
年的实际资本存量。以2002年为基期,本文分别用各地区历年工业品出厂价格指数、原材料价格指数、固定资产投资价格指数对企业产出值、中间投入和资本投入进行价格平减,其中的价格指数均来自《中国统计年鉴》和《中国工业统计年鉴》。地区总量生产率则定义为所有企业全要素生产率的加权平均,具体形式为:

其中,θit表示的是用企业生产份额来衡量的权重变量,通过用企业的产值除以该地区总产值求出。
(二)中国跨地区全要素生产率测算
本文使用的样本数据来源于《中国工业企业数据库》和锐思金融研究数据库,在处理样本数据的过程中,依据标准的数据剔除程序(Levinsohn and Petrin,2003;谢千里,2008;聂辉华,2008)[5,18-19],剔除了异常的观测值。本文对区域的划分按照世界银行(2006)[20]的标准,将全国31个省级行政区域划分为六大经济区域,分别为东北、东南、环渤海、中部、西北和西南。由于环渤海与东南地区、西北与西南地区的变化特征较为一致,本文则将环渤海和东南地区作为一个整体进行分析,类似地,将西北和西南地区也作为一个整体进行分析,其中东北地区包括吉林、辽宁和黑龙江;中部地区包括湖南、湖北、安徽、江西和河南;环渤海和东南地区包括北京、河北、天津、山东、江苏、上海、福建、广东和浙江;西北和西南地区包括陕西、山西、内蒙古、宁夏、新疆、青海、甘肃、重庆、四川、云南、广西、贵州、海南和西藏。
表1列出了2002-2014年中国31个省份的TFP水平值与增长率。总的来说,从TFP水平指标来看,中国地区层面生产率最高的是环渤海和东南地区。具体到省份,将生产率按照从高到底的顺序排名依次为:上海、福建、广东、北京、山东、浙江、江苏、天津和河北。其中,地区总量生产率最高的是上海,TFP达到了8.23,位居全国第一,这表明上海的市场经济发达程度是最高的。其余8个省份的地区总量生产率在样本考察期间普遍都处于全国领先的水平。其次,中国地区总量生产率排名第二是中部地区。按照TFP的高低排名依次是湖北、安徽、湖南、江西和河南。其中,湖北和安徽的地区TFP最高,分别达到为7.44和7.41,可见湖北和安徽的市场经济发达程度在中部地区最高,而河南的TFP在中部地区是最低的,只有6.88,可见河南在中部地区经济发展是相对落后的。再次,中国地区总量生产率相对较低的是东北地区。其中,吉林的TFP相对较高,达到了7.11,可见吉林的经济发展水平在样本考察期间是东北地区经济相对比较发达的省份,其次较高的是辽宁,地区TFP为7.03;而黑龙江在东北地区经济发展水平相对较低,地区TFP只有6.61。最后,中国西南和西北地区各省份的总量生产率相对其他地区是最低的。生产率在西南和西北地区排名靠前的是山西、陕西、四川、海南和重庆,其中山西和陕西的TFP分别为7.58和7.56。而新疆和宁夏几乎排在了全国最末,地区TFP只有6.57和6.03。可见,西南和西北地区各省份之间的经济差距较大而且经济发展落后于中国其他地区。
3) 温度。当浸提温度<40℃时,随着温度升高火龙果果皮甜菜苷类色素提取量呈逐渐上升趋势;当温度增至40℃时提取量最高,为3.85 mg/100g;之后呈快速下降趋势,其原因可能是甜菜苷类色素对温度较敏感,过高的温度加速了甜菜苷类色素的分解[14]。因此,浸提温度以40℃最优。
从TFP增长率指标来看,可以发现2002-2014年中国地区总量TFP均出现上升的趋势,都有着较高TFP增长率。其中,经济相对落后的区域如西南和西北地区及东北地区生产率增长率相对较高,而经济相对发达的环渤海和东南地区生产率增长率放缓。这意味着中国工业企业在总体上存在着收敛的趋势,这和谢千里等(2008)使用参数方法测量TFP获得结果一致。

表1 2002-2014年中国31个省份的TFP水平值与增长率
四、中国跨地区全要素生产率差异原因分析
对于中国跨地区全要素生产率的差异的原因,可以从以下三个方面进行分析,包括知识进步、资源配置和政策因素。
(一)知识进步
新经济增长理论认为,知识进步是推动经济增长的一个重要因素。中国长期以来存在着“轻研发,重引进”的思想。在20世纪80年代,中国工业技术发展水平与发达国家的差距很大,因此通过引进国外先进技术可以促进生产率的增长。但是,随着这种差距的不断缩小,发达国家不愿意再向中国转让先进技术,因此,仅仅依靠技术的引进来提高生产力的效果会不断变差。而且中国引进先进技术是从发达的地区如环渤海和东北地区开始的,由于技术的流动存在着一些制约因素,因而导致了中国四大区域的技术水平产生差异。同时,由于东北、中部及西南和西北地区的科技成果向市场转化的程度也比较低,因此制约了这些地区的经济发展水平,从而表现为这三个区域的TFP相较于环渤海和东南地区的TFP较低。
(二)资源的配置效果,主要包括市场化、城市化和产业结构
市场化进程的关键在于:市场位于资源合理配置的主导地位、非国有经济发展加快、政府直接干预经济活动频率减少等。环渤海和东南地区位于中国改革开放的最为前沿的地带,拥有非常优越的地理位置和极为雄厚的经济实力,吸引了大量的人才(人力资本)和资金(物质资本)向该区域进行集聚,并且在2003年中国政府加大对环渤海和东南地区的政策优惠和提供更多的资源,使得该区域的市场经济更加发达,市场经济更加成熟,从而市场机制得以有效发挥,促使了该区域资源配置情况的大幅度改善,因而资源配置效果最好。而中部地区人口数量大,市场化程度明显低于环渤海和东南地区,主要表现在:非国有经济所占的比重小、政府直接干预经济活动和资源的配置范围比较广、对外开放水平低、引入外资程度低等,因而导致了生产要素和劳动力的大量流失,市场份额减少,所以资源误配置程度要高于环渤海和东南地区。但是在2003年中国提出“加强中部地区之崛起”的战略目标后,中部地区的市场化程度和开放度得到提高,资源误配置程度得到很大的改善,各地区TFP水平有所提高。而东北地区和西南和西北地区的国有企业和集体经济在经济中起着非常重要的作用,所占份额比重很高,导致了生产率较高的民营企业规模却不是较大的,反之生产率较低的国有企业规模却是很大的,因此影响了该地区的资源配置效果,使得TFP水平较低。在城市化方面,在改革开放初期阶段,国有企业因为体制的制约缺乏竞争力,而沿海地区的民营企业凭借着市场导向和较低的劳动力成本迅速占领市场。同时,首先快速发展起来的民营企业通过引进先进技术、人才和产权改制等改进了经营模式,在市场上占领了资源的优势,从而使得中国跨地区生产率发生了差异。而产业机构的调整对经济的增长也起了很大的推动作用。但是,不管是在20世纪80年代初期的中国工业结构转向了轻型化还是在90年代中国工业结构的重新转向重型化,都聚集发生在环渤海和东南地区的一些省份,中部、西部地区的一些省份在转换的程度上远远落后于环渤海和东南地区,因此导致了中国四大区域经济发展的差异。
(三)政策因素
中国改革实行的是从局部到整体的循序,并且政策向东部沿海地区倾斜,因此给环渤海和东南地区提供了更多政策支持和更多的自主权。同时,对投资、财政、计划、税收、价格、信贷、工资等各领域进行了全面的改革,逐步提高了市场机制在资源配置中的发挥作用。但是这种改革体制在客观上也造成了中国四大区域之间经济发展机会的不均等,从而使得跨地区生产率产生较大的差异。
五、结论与政策建议
本文利用2002-2014年中国工业企业水平的数据,采用LP半参数方法估算了中国各个区域和31个省份的全要素生产率,并在此基础上从知识进步、资源配置和政策因素等三个方面分析了跨地区生产率差异原因,结果表明中国跨地区生产率具有较大差异,其中环渤海和东南地区及中部的TFP均值最高,其次是东北地区,西南和西北地区TFP均值最低。这是因为环渤海和东南地区及中部地区位于改革开放的前言地带,经济体制改革最为彻底,市场化程度和城市化程度最高,并且中国引进先进技术是从该区域开始的,政策也向沿海地区倾斜,因此给环渤海和东南地区提供了更多政策支持和更多的自主权,所以该区域经济发展速度最快,而东北及西南和西北地区的TFP均值比较低,这是由于这两个区域技术引进水平不高,国有企业份额比重大,缺乏市场竞争力,并且产业结构调整和城市化建设相对较慢,因此导致了这两个区域TFP均值较小。要改善中国不同地区的生产率差异程度,中国政府的政策和制度安排需要从以下几个方面进行改善。
第一,全面实施创新驱动发展战略,加快各地区形成以创新为主要引领和支撑的发展模式,拓展发展新空间。政府相关部门要加大鼓励企业科技创新、产业创新、产品创新和市场创新,增加自主创新能力和自我学习意识,提高技术进步和技术效率,促进不同地区间的技术溢出效应,并鼓励发展产业集聚来提高企业和地区的经济效率。这不仅有利于应对新旧经济发展动力衔接,也有利于产业结构调整和转型升级。政府还要加快改造提升传统工业,将传统以资源和要素驱动的发展方式转向为以创新驱动和发展质量为中心,依靠科学技术和人力资本及管理创新的发展模式。进一步深入推进信息化与各产业的协同和融合,发挥城市群的辐射带动作用,引导构建产业技术创新联盟,推动跨领域跨行业协同创新,促进科技与经济深度融合,促进较发达地区形成“追赶效应”。
第二,加强对落后地区产业政策的完善和扶持力度,加快科技体制和金融市场化的改革进程,积极优化资源配置。政府要进一步加大对落后地区如西部地区的发展扶持力度,加大金融支持、人力资本、科学研究等要素投入和税收优惠力度,促进要素积累,提高要素边际生产率。进一步深入实施西部大开发,支持西部地区改善基础设施,发展特色优势产业。同时,政府相关部门要减少金融机构对非国有企业和中小企业的信贷歧视,并改变金融机构对集体企业和国有企业的信贷政策倾斜的现状,降低金融市场进入壁垒、放松政策限制,鼓励和引导非国有资本进入金融业,加速银行业的竞争,促进要素有序资源流动,提高资源配置效率和金融服务实体经济效率,从而从根本上缩小地区生产率差异。
第三,降低地区边界效应,打破技术转移壁垒。地区边界效应不仅包括地方保护政策和贸易壁垒,还包括体制障碍和技术壁垒。因此,政府不仅要不断完善地方政府的激励机制,进一步加强中国各地区的通信设施、交通运输和公共设施的建设,消除各地区的市场进入壁垒和垄断势力,制定更加合理的贸易政策,还要拓宽地区间技术扩散的广度和深度,打破地区间技术转移壁垒,提高对外开放程度,建立落后地区引进和学习先进地区技术的保障机制,通过提高企业竞争力来缩小地区生产率差异。
参考文献:
[1]Basu S,John G Fernald.Returns to Scale in US Production:Estimates and Implications[J].Journal of Political Econo⁃my,1997,105(2):249-283.
[2]Easterly W,Levine R.It is not Factor Accumulation:Styl⁃ized Facts and Growth Models[J].World Bank Economic Review,2001,15(2):177-219.
[3]Auer Raphael A.Human capital and the dynamic effects of trade[J].Journal of Development Economics,2015,117(7):105-118.
[4]Olley G Steven,Ariel Pakes.The Dynamics of Productivi⁃tyintheTelecommunicationsEquipmentIndustry[J]. Econometrica,1996,64(6):63-97.
[5]Levinsohn James,Amil Petrin.Estimating Production Func⁃ tions Using Inputs to Control for Unobservables[J].Review of Economic Studies,2003,70(4):317-341.
[6]李平,钟学义,王宏伟,等.生产率变化与经济增长源泉:1978~2010年[J].数量经济技术经济研究,2013(1):3-21.
[7]杨茜淋.我国工业分行业全要素生产率估计[J].商业时代,2013(16):115-117.
[8]张建升.省域全要素生产率地区差异的动态演进[J].经济经纬,2011(6):37-41.
[9]蒲勇健,余显兰,张勇.中国再生资源产业的技术效率及影响因素研究——基于随机前沿超越对数生产函数的分析[J].工业技术经济,2014(12):3-10.
[10]余泳泽,张妍.我国高技术产业地区效率差异与全要素生产率增长率分解——基于三投入随机前沿生产函数分析[J].产业经济研究,2012(1):44-53.
[11]段文斌,尹向飞.中国全要素生产率研究评述[J].南开经济研究,2009(2):130-140.
[12]孙庆兰.基于数据包络分析法的流通与制造业TFP交叉作用分析[J].商业经济研究,2015(2):15-16.
[13]石腾超,邹一南.我国制造业全要素生产率区域差异及其原因研究——基于制造业2003-2011年面板数据的实证分析[J].区域经济评论,2014(1):130-137.
[14]孙晓华,王昀,郑辉.R&D溢出对中国制造业全要素生产率的影响——基于产业间、国际贸易和FDI三种溢出渠道的实证检验[J].南开经济研究,2012(5):18-35.
[15]张杰,李勇,刘志彪.出口促进中国企业生产率提高吗?来自中国本土制造业企业的经验证据[J].管理世界,2009(12):11-26.
[16]余淼杰.中国的贸易自由化与制造业企业生产率[J].经济研究,2010(12):97-110.
[17]Paquet A,Robidoux B.Issues on the Measurement of the Solow Residual and the Testing of Its Exogeneity Evidence for Canada[J].Journal of Monetary Economics,2001,47:33-58.
[18]谢千里,罗斯基,张轶凡.中国工业生产率的增长与收敛[J].经济学(季刊),2008(3):45-56.
[19]聂辉华,松涛,王宇锋.创新企业规模和市场竞争——基于中国企业层面面板数据的证据[J].世界经济,2008,7(2):15-24.
[20]世界银行.中国政府治理、投资环境与和谐社会:中国120个城市竞争力的提高[C].杭州:第四届中国投资环境论坛论文集,2006.
[责任编辑:余志虎]
中图分类号:F061.5;F124
文献标志码:A
文章编号:1007-5097(2016)03-0050-07
收稿日期:2015-07-23
基金项目:国家社会科学基金项目(07BJY074);陕西省软科学研究计划项目(2013KRM12)
作者简介:张倩肖(1966-),女,陕西西安人,教授,博士生导师,研究方向:产业经济学,宏观经济学;李丹丹(1990-),女,河南济源人,博士研究生,研究方向:产业经济学。
A Study on the Transregional Total Factor Productivity in China Based on the Semi-parametric Method
ZHANG Qian-xiao,LI Dan-dan
(School of Economics and Finance,Xi’an Jiaotong University,Xi’an 710061,China)
Abstract:Based on the micro data of the level of China’s industrial enterprises from 2002 to 2014,this paper applies Levinsohn and Pertrin method(hereinafter referred to as LP method)systematically analyzes and measures the changes in the total factor productivity(TFP)of China’s 31 provincial-level administrative areas,and compares the differences in productivity between different areas and analyzes the reasons for the differences.The results show that the transregional total factor productivity in China has great differences,among them the TFP mean value is relatively high in Bohai Sea,the southeast and central regions,followed by the northeast region,and the southwest and northwest regions with the lowest mean TFP.Therefore,the government needs to make more efforts on fully implementing innovation driven development strategy,perfecting industrial policy,optimizing resource allocation,reducing regional boundary effect and so on,in order to improve the TFP differences between different regions in China.
Keywords:TFP;LPsemi-parametric method;regional differences

