飞翼布局无人机滑跑纠偏控制

王彦雄, 周洲, 邵壮, 祝小平



飞翼布局无人机滑跑纠偏控制

王彦雄1, 周洲2, 邵壮1, 祝小平3

摘要：针对滑跑纠偏控制律对良好鲁棒性的要求，以及飞翼布局无人机地面滑跑六自由度模型非线性、多变量的特点，提出了基于自抗扰控制理论的无人机非线性滑跑纠偏控制律；由于采用了前轮转向、阻力方向舵和主轮差动刹车联合纠偏，针对控制执行机构纠偏效率在滑跑过程中变化较大，以及阻力方向舵和刹车机构兼具减速和纠偏功能的特点，提出采用加权伪逆法对偏航力矩及阻力控制指令进行动态控制分配。结果表明，自抗扰滑跑纠偏控制律能够能有效观测并补偿跑道环境影响造成的强烈干扰及侧风干扰，加权伪逆法能够对偏航力矩和阻力指令进行动态分配，并使各执行机构使用量处于正常范围以内。

关键词：角速度；扰动补偿；无人机；飞翼布局；纠偏控制；自抗扰；伪逆法；复合控制

高空长航时大型飞翼布局无人机，多采用轮式起降方式。相对有人机而言无人机的机场条件比较简陋，而战时更可能会使用高速公路等作为起降跑道，因此无人机起降滑跑过程中不可避免地会受到跑道环境(如部分区域存在道面湿润、积水和积雪等情况)以及侧风等影响，而目前针对存在跑道环境影响的滑跑纠偏控制律研究较为少见。

文献[1]建立了包含起落架、刹车装置及跑道特性的无人机滑跑非线性全量数学模型，并利用遗传算法对主轮差动刹车和方向舵联合纠偏控制律参数进行设计。文献[2]提出采用方向舵、主轮差动刹车和前轮转向的联合纠偏控制方案，并采用经典控制理论设计纠偏控制律参数。但上述文献均在特定滑跑速度下对控制律参数进行整定，由于无人机滑跑模型较强的非线性特征，控制器很难满足高速与低速同时适用。文献[3]在经典PID控制器的基础上，分别设计不同速度下的控制律参数，然后设计模糊控制器使PID控制器能在不同速度下使用相匹配的参数，但该方法需对众多速度点设计参数使得调参工作较为繁琐。因此针对非线性较强的无人机滑跑模型可采用非线性控制理论设计滑跑纠偏控制律。

随着滑跑速度的变化，各种纠偏执行机构效率变化较大，文献[1-2]中使用离线整定的参数对控制指令进行分配的方式不能在着陆滑跑全过程中对执行机构进行充分有效的利用。因此有必要对以执行机构效率为依据的动态控制指令分配方法进行研究。Wayne[4]针对舵面分配提出了伪逆法，徐明兴等[5]将该方法应用于多螺旋桨太阳能无人机的推力分配，具有借鉴意义。

本文针对飞翼布局无人机地面滑跑六自由度非线性模型设计了基于自抗扰控制理论的非线性滑跑纠偏控制律，提出采用加权伪逆法对偏航力矩和阻力指令进行动态控制分配。最后以某大展弦比飞翼布局无人机为对象进行仿真，验证所设计控制系统对跑道环境影响和侧风干扰的抑制能力及动态控制分配的有效性。

1飞翼布局无人机滑跑模型及特点

1.1坐标系及坐标系间的转移矩阵

本文采用坐标系与文献[6]相同，为更方便研究轮胎与地面的作用力，还需定义一个新的坐标系。基于文献[6]并去除其无人机滑跑过程中滚转角φ为零的设定，定义稳定坐标系osxsyszs如下:取无人机质心为原点,osxs轴位于机体对称平面内并平行于地面指向前,oszs轴垂直于地面指向下,osys轴垂直于osxszs平面指向右。由稳定坐标系到机体坐标系间的转移矩阵如下

(1)

式中:θ为俯仰角;φ为滚转角。

1.2无人机滑跑动力学与运动学方程

文献[1]建立了无人机地面滑跑非线性全量数学模型,本文参照文献[1]推得无人机地面滑跑动力学与运动学方程如下

(2)

(3)

(4)

(5)

(6)

(7)

(8)

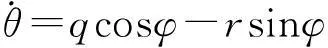
(9)

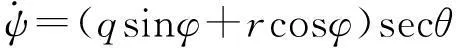
(10)

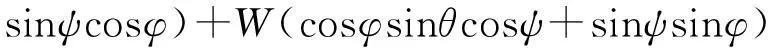
(11)

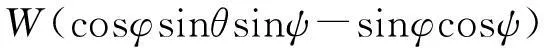
(12)

(13)

式中:U、V和W分别为无人机速度在机体轴系obxb、obyb和obzb3个方向的分量;p、q和r分别为无人机角速度在机体轴系obxb、obyb和obzb3个方向的分量;ψ为偏航角;α为迎角;β为侧滑角;xg、yg和zg分别为无人机在地轴系ogxg、ogyg和ogzg3个方向的位移;M为无人机质量;g为重力加速度;Ixx、Iyy和Izz分别为无人机绕机体轴系obxb、obyb和obzb三轴的转动惯量;Ixz为惯性积;D、Y和L分别为气动阻力、气动侧力和气动升力;T为推力;l、m和n分别为由气动力产生的滚转、俯仰和偏航力矩;Fx、Fy和Fz分别为地面对无人机的作用力在机体轴系3个方向的分量;Mx、My和Mz分别为地面对无人机的力矩在机体轴系3个方向的分量。

风干扰对无人机空速、迎角和侧滑角的影响和风梯度对气动力矩系数的影响详见文献[7],文中不再赘述。

1.3地面对无人机的作用力及力矩

无人机在滑跑过程中地面对无人机的作用力如图1所示。

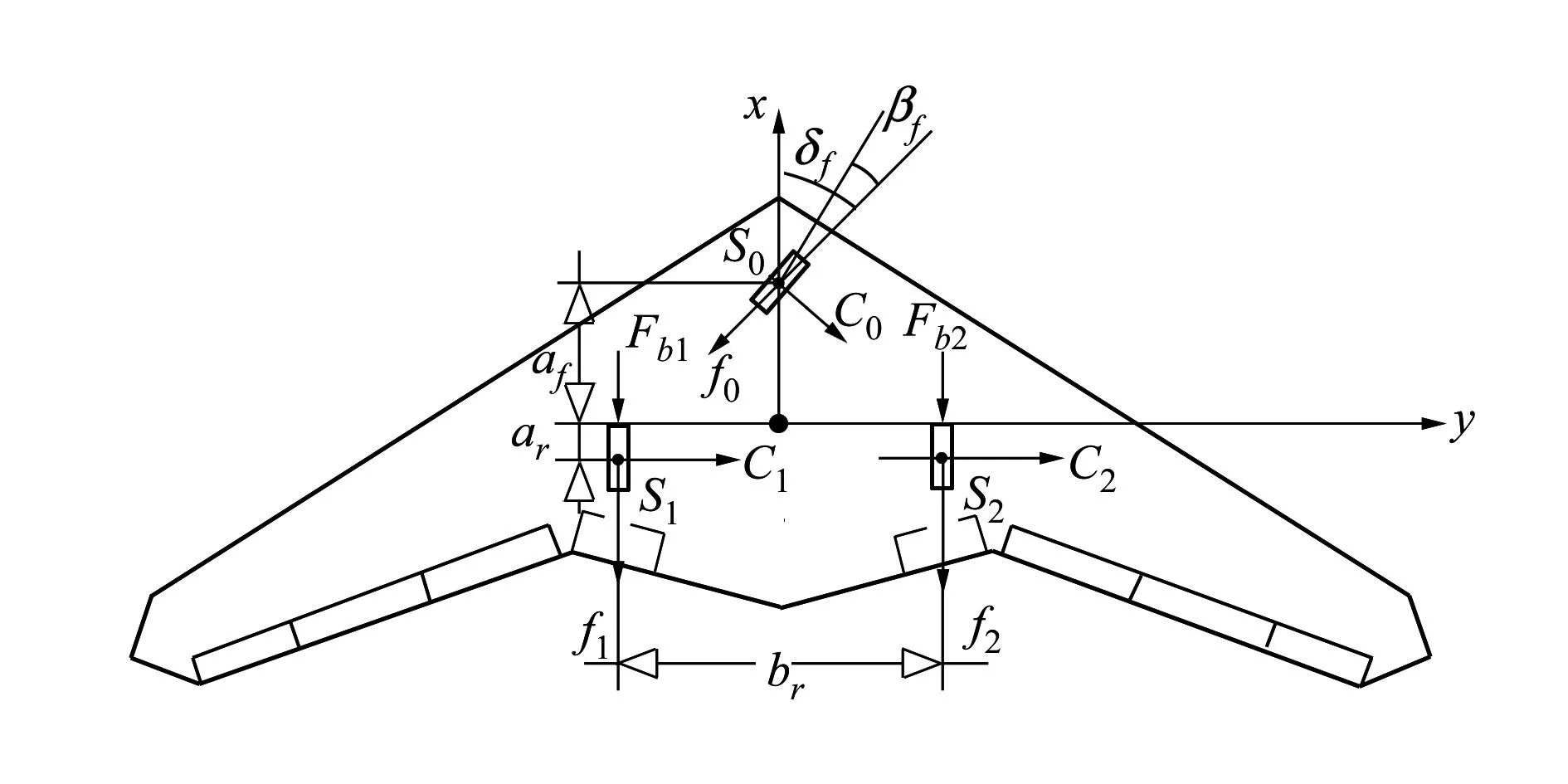
图1　地面对无人机的作用力

图1中:S0、S1和S2分别为地面对无人机前轮、左主轮和右主轮的支撑力(由各轮中黑点表示),方向近似垂直向上;C0、C1和C2分别为地面对前轮、左主轮和右主轮的侧向力;f0、f1和f2分别为前轮、左主轮和右主轮的滚动摩擦力;Fb1和Fb2分别为左主轮和右主轮轮胎与地面的结合力;δf为前轮与机体对称面的夹角;βf为前轮侧偏角;af和ar分别为前轮和主轮与无人机重心的纵向距离;br为主轮间距。将轮胎视为刚体,则S0、S1和S2与缓冲器压缩量及伸缩速度相关,将缓冲器简化为弹簧-阻尼系统则有

(14)

式中:Δl0、Δl1和Δl2分别为前、左和右起落架缓冲器的压缩量;Kf和Kr分别为前和主起落架缓冲器的等效弹簧刚度;Cf和Cr分别为前和主起落架缓冲器的等效阻尼系数。根据机身与起落架的几何关系可得

(15)

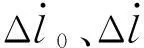
机轮的滚动摩擦力及主轮轮胎与地面的结合力表示如下

(16)

(17)

式中:μf和μr分别为前轮和主轮的滚动摩擦系数;μ1和μ2分别为左、右主轮轮胎与地面的结合系数。根据Burckhardt模型[8]结合系数可由如下公式得到

(18)

式中:Us为无人机速度在稳定坐标系osxs轴的分量;λ1为左主轮滑移率;系数c1至c3详见文献[8]。

结合系数μ与滑移率的关系曲线如图2所示。

(19)

式中:ω1为左主轮转速;R为主轮半径。

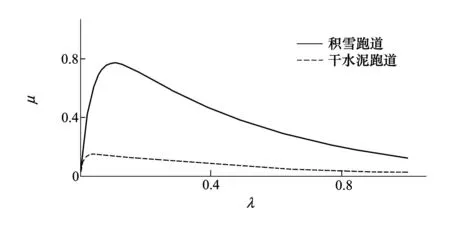
图2　μ-λ曲线

(20)

式中:Fy0为机体轴系obyb方向上除主轮侧向力外的其他地面力分量之和。

前轮侧向力C0由下式求得

(21)

(22)

式中:kbf为前轮侧偏刚度,θf为前轮速度方向与机体对称面的夹角,可由下式求得

(23)

式中:Vs为无人机速度在稳定坐标系osys轴的分量。当不使用前轮转向控制时δf与θf相等。

综上,地面对无人机的作用力及力矩在机体轴系三方向的分量可由下式求得

(24)

(25)

2基于自抗扰的非线性滑跑纠偏控制律

图3为滑跑纠偏控制系统结构框图,图中:下标c代表上级回路产生的虚拟指令;ntc和Dtc分别为期望偏航力矩指令和期望阻力指令;δrl和δrr分别为阻力方向舵左、右舵的舵偏;Mb1和Mb2分别为左右主轮刹车力矩。

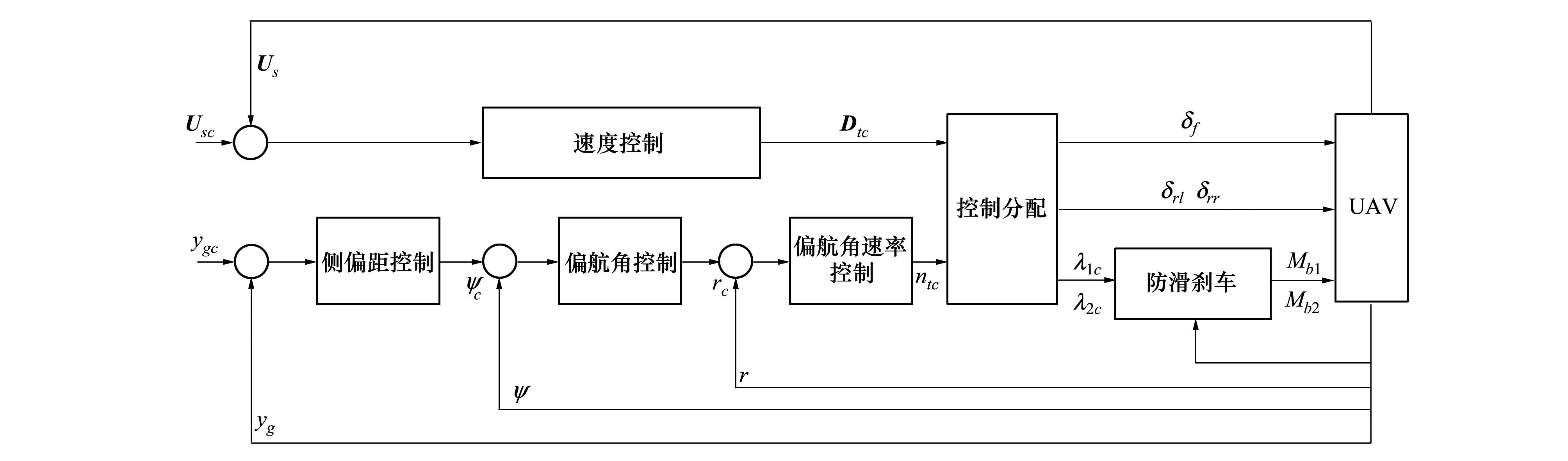
图3　滑跑纠偏控制系统结构框图

如图3所示,非线性滑跑纠偏控制律分为速度子系统控制律和位置子系统控制律,其中后者根据时标分离思想设计为三级一阶串级结构,并采用自抗扰控制技术[9]逐层设计虚拟指令。

第一级:当偏航角ψ较小时有sinψ≈ψ,(12)式可以表述为如下形式

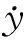
(26)

式中

式中:x代表无人机非线性全量模型中12个状态变量。

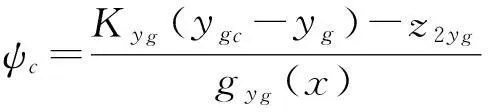
(29)

式中:Kyg为位置控制律增益。

第二级:(10)式可以表述为如下形式

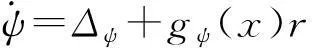
(30)

式中

Δψ=qsinφsecθ

(31)

gψ(x)=cosφsecθ

(32)

偏航角速率虚拟指令设计如下

(33)

式中:Kψ为姿态控制律增益;z2ψ为不确定项Δψ的估计值。

第三级:偏航角速率r的微分方程为动力学方程,其不确定项除模型已知部分fr(x)外,还包含由侧风引起的外扰以及建模误差之和dr(t),以及由跑道环境影响与执行机构效率非线性所导致的,执行机构产生的偏航力矩实际值与指令值间的误差Δn和gr(x)之积gr(x)Δn。因此不确定项Δr表示为Δr=fr(x)+gr(x)Δn+dr(t)

(34)

(35)

fr(x)为除去执行机构操纵力矩的剩余部分。

(36)

(37)

式中:z2r为不确定项Δr的估计值。

(38)

(39)

式中:uxi由一至三级回路依次为ψ、r、ntc;β1xi和β2xi为扩张状态观测器参数;z1xi和z2xi分别为扩张状态观测器对状态变量xi和不确定项Δxi的估计值。

(40)

只要选择合适的参数使得扩张状态观测器稳定,则稳态时有如下收敛关系z1xi→xi,z2xi→Δxi得到不确定项Δxi的估计值,将其代入(29)式、(33)式、(37)式所示控制律进行补偿,显然可以提高系统的鲁棒性，二阶扩张状态观测器参数整定详见文献[10]。

对于速度子系统控制律设计,采用动态逆控制理论。由无人机滑跑全量非线性数学模型和(1)式可推导无人机速度在稳定坐标系osxs轴分量的微分方程为

式中

速度控制虚拟指令如下

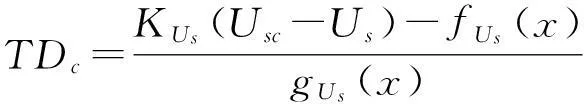
(45)

式中:KUs为速度控制律增益。

由于无人机滑跑过程中δf、φ、θ及α数值较小,且速度控制精度要求相对较低,根据(41)式并忽略小量后有

式中:Db为机体气动阻力。

由速度控制虚拟指令TDc可得到期望推力指令Tc和期望阻力Dtc指令。

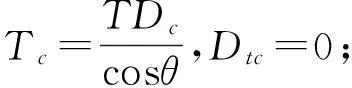
当TDc<0时,有Tc=0,Dtc=-TDc;

推力T和油门δt的关系曲线可由试验得到

T=f(δt,H,Ma)

(48)

根据期望的推力指令,由(48)式可得到油门指令δt。

3动态控制分配

本文采用前轮转向、阻力方向舵和主轮差动刹车作为联合纠偏执行机构,由此带来2个问题:①执行机构的纠偏效率会随滑跑速度的改变而发生较大的变化,其中前轮转向和主轮差动刹车的纠偏效率与机轮和地面的压力成正比,无人机滑跑速度较高时升力较大而压力相应减小,因此其纠偏效率随滑跑速度的增加而减小,阻力方向舵的纠偏效率与动压成正比,因而其纠偏效率随滑跑速度的增加而增大;②阻力方向舵和刹车机构兼具纠偏和减速功能,且减速效率也随速度变化而变化。因此应当采用一种控制分配方法,能够依据执行机构的效率对偏航力矩与阻力指令进行动态分配。

加权伪逆法实现简单、实时性好,在当前工程设计中具有重要的应用价值,本文采用该方法对控制指令进行动态控制分配。

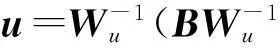
(49)

式中:Wu为m×m秩为m的加权矩阵，v为期偏航力矩阵与阻力向量；u为执行机构使用量。

(50)

式中

b11=-kbfafcosδfcosθcosφ

b14=-0.5brkλS1cosθcosφ

b15=0.5brkλS2cosθcosφ

b24=kλS1

b25=kλS2

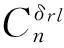
虚拟控制v设计为

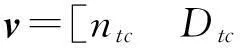
(51)

纠偏执行机构的使用量u设计为

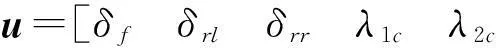
(52)

加权矩阵Wu设计为

式中:λ1c和λ2c分别为左、右主轮的期望滑移率;下标max代表执行机构使用量最大值;参数K1和K2可通过仿真进行整定。

当阻力指令较小时,根据加权伪逆法可能得到小于零的阻力方向舵舵偏或期望滑移率,由于上述2种执行机构不能执行小于零的使用量,因此需对执行机构使用量进行再分配。另外,由于阻力方向舵和主轮差动刹车的使用不可避免会产生阻力,且速度控制精度要求相对较低,因此再分配时仅将偏航力矩指令作为虚拟控制。

具体做法如下:

第1步:由(49)式求得各执行机构使用量;

第2步:判断是否存在δrl<0、δrr<0、λ1c<0、λ2c<0的结果,如果没有,则结束流程,如果有,则进行下一步;

第3步:判断是δrl<0或λ1c<0,还是δrr<0或λ2c<0,若为前者,则令i=1,若为后者,则令i=2,执行如图4所示流程,然后返回第2步。

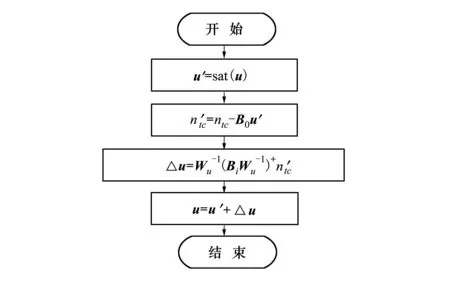
图4　再分配流程

图4中Bi设计如下

sat函数设计如下

(57)

式中:uj代表向量u第j位元素。值得注意的是,函数sat对u1即δf无效。

4仿真实验

对某型大展弦比高空长航时飞翼布局无人机进行滑跑仿真,假设防滑刹车能够理想地跟踪期望滑移率。控制律参数如表1所示。

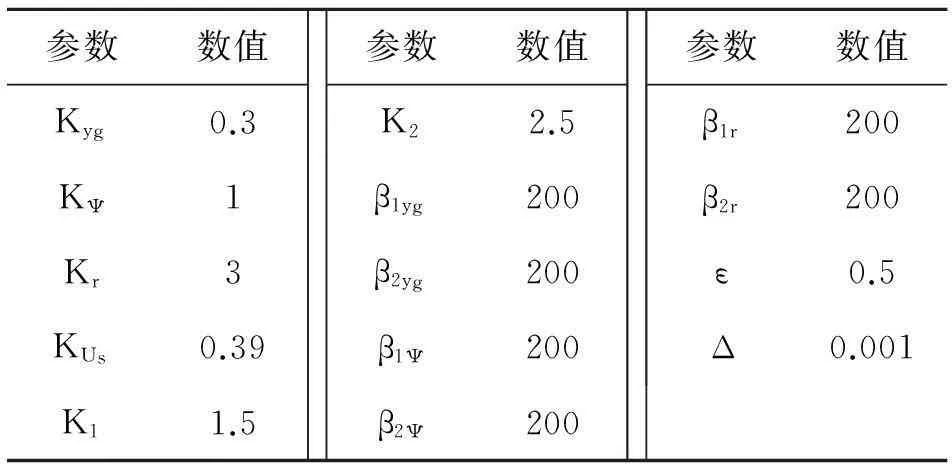
表1　控制律参数

仿真中将主要考虑2种扰动:

1)考虑侧风干扰,在仿真中加入最大风速为的10m/s半波长正侧风,其风速由0开始至xg=200m处达到最大值。

2)跑道部分区域可能出现道面湿润、积水、积雪以及积冰等情况。若无人机在着陆滑跑过程中,左、右主轮所处道面不同情况下进行刹车减速,由于μ-λ曲线的差异,不仅相同滑移率下两轮结合系数不同,而且在不同道面状况下的结合系数最大值也不相同,2轮结合力的不同就会导致航向干扰力矩产生,道面差异越大则干扰越强烈,并且即使防滑刹车能够有效跟踪期望滑移率,但由于μ-λ曲线的改变,使得期望的结合力得不到实现,那么由主轮差动刹车得到的偏航力矩与指令间就会存在误差,道面差异越大则该误差越大。上文中的航向干扰力矩也可以理解为刹车初始时刻偏航力矩实际值与指令值间的误差。

为验证所设计滑跑纠偏控制系统在跑道环境影响下抑制干扰的能力,仿真中设定部分跑道被积雪覆盖,无人机滑跑过程的前50m左主轮处于积雪道面,而右主轮处于干水泥道面。

无人机质量为5 500kg，稳定坐标系下无人机初始速度为60m/s,仿真结束条件为无人机减速至10m/s进入跑道滑行阶段。仿真步长1ms。

为比较自抗扰滑跑纠偏控制律及动态控制分配与传统控制方法的不同特点,下图中还给出了相同仿真环境下,PID滑跑纠偏控制律结合动态控制分配控制方法的仿真结果,其中PID控制律参数在不同速度段下进行整定,仿真中通过线性插值,使控制律在不同速度下的使用与该速度相匹配的参数。2种方法在图中分别以“ADRC”和“PID”表示。

首先对仅存在侧风干扰的情况进行仿真。

然后对部分跑道被积雪覆盖的情形进行仿真。

图5　无人机侧偏距变化曲线　　　　图6　无人机侧偏距变化曲线　　　　　　图7　无人机速度变化曲线

图8　偏航力矩变化曲线　　　　　　　图9　偏航力矩变化曲线　　　　　　图10　不确定项跟踪曲线

图8中，n1、n2、n3分别代表由阻力方向舵、主轮差动刹车和前轮偏转产生的偏航力矩。结合图7,仿真开始后由速度控制律给出阻力指令,无人机进行刹车减速,由于左主轮处于积雪道面而右主轮处于干水泥道面,刹车减速时右主轮结合系数迅速上升到0.72,但如图2所示,左主轮结合系数只能停留在0.16附近。图8给出了仿真开始2s内由纠偏执行机构实际产生的偏航力矩变化曲线,由于两主轮结合力之间的差距较大,由刹车造成的偏航力矩迅速上升到15 000N·m左右,使无人机受到了强烈的干扰力矩。

如图10所示,对于“ADRC”,受到干扰后扩张状态观测器迅速对不确定项Δr作出有效估计,偏航力矩指令值与实际值之差Δn与gr(x)的积为主要部分,通过对Δr估计值在控制律(37)中进行补偿,控制律将及时给出更大的负方向偏航力矩指令。从图8可以看出,受扰后由阻力方向舵和前轮产生了较“PID”更大的负方向偏航力矩,由图9,“ADRC”使得执行机构产生偏航力矩之和nt的正向增大很快得到抑制,并迅速减小。由图6可以看出,在自抗扰控制律的作用下,无人机始终维持在跑道中心线附近,最大偏离不到0.23m。

但对于“PID”,直到无人机偏离中心线后,控制律才会给出负向的偏航力矩指令,但由于“PID”控制律不能对指令值与实际值之差做出估计补偿,控制律给出的指令仅为两主轮均处于干水泥道面时,相同侧偏距误差下的数值,显然由于跑道环境影响,使得该指令得不到准确跟踪,实际产生的偏航力矩不足以使无人机维持在跑道中线附近。因此在图9中,实际偏航力矩之和nt在仿真开始后迅速增大到10 000N·m附近,使得偏航角迅速增大,如图6所示，无人机偏离跑道中线接近22m,参考我国民用机场45～60m的宽度,显然无人机已处于跑道边缘。

由此自抗扰滑跑纠偏控制系统的鲁棒性得到了验证。此外,对于“ADRC”,仿真过程中,阻力方向舵最大舵偏为72°,最大刹车力矩为2 650N·m,前轮最大舵偏为-4.4°。参考阻力方向舵的舵偏范围为0～90°,前轮偏转范围为-5～5°,刹车力矩可用范围为0～12 000N·m,显然各执行机构的使用量均在正常范围以内,说明了自抗扰滑跑纠偏控制律结合动态控制分配控制方法的合理性和可行性。

5结论

1) 基于自抗扰的非线性滑跑纠偏控制结合动态控制分配的控制方法能够有效抑制跑道环境影响造成的强烈干扰及侧风干扰，使无人机在着陆滑跑过程中，始终维持在跑道中心线附近；

2) 动态控制分配能够依据执行机构效率对偏航力矩和阻力指令进行有效分配，使得在着陆滑跑全过程中，各执行机构的使用量均处于正常范围以内。

参考文献：

[1]王勇,王英勋. 无人机滑跑纠偏控制[J]. 航空学报, 2008, 29(suppl1): 142-149

WangYong,WangYingxun.LateralDeviationCorrectionControlforUAVTaxiing[J].ActaAeronouticaetAstronauticaSinica, 2008, 29(suppl1): 142-149 (inChinese)

[2]郝现伟,杨业,贾志强,等. 无人机着陆滑跑数值模型与纠偏控制[J]. 电机与控制学报, 2014, 18(5): 85-92

HaoXianwei,YangYe,JiaZhiqiang,etal.MathematicModelandDeviation-CorrectionControlforUAVTaxiing[J].ElectricMachinesandControl, 2014, 18(5): 85-92 (inChinese)

[3]吴成富,闫冰,邵朋院. 基于模糊控制的无人机滑跑起飞控制方法研究[J]. 西北工业大学学报, 2015, 33(1): 33-39

WuCengfu,YanBei,ShaoPengyuan.ExploringTaxiingTake-OffControlforUnmannedAerialVehicle(UAV)BasedonFuzzyControl[J].JournalofNorthwesternPolytechnicalUniversity, 2015, 33(1): 33-39 (inChinese)

[4]WayneCD.ConstrainedControlAllocation[J].JournalofGuidance,Control,andDynamics, 1993, 16(4): 717-725

[5]徐明兴,祝小平,周洲,等. 多螺旋桨太阳能无人机推力分配方法研究[J]. 西北工业大学学报, 2013, 31(4): 505-510

XuMengxing,ZhuXiaopeng,ZhouZhou,etal.ExploringanEddectiveMethodofThrustAllocationforSolar-PoweredUAVwithMultiplePropellers[J].JournalofNorthwesternPolytechnicalUniversity, 2013, 31(4): 505-510 (inChinese)

[6]王鹏. 飞翼式长航时无人机轮式起降控制技术研究[D]. 西安: 西北工业大学, 2009

WangPeng.StudyonControlofTake-OffandLandingwithWheelsforFlying-WingLongEnduranceUAV[D].Xi′an,NorthwesternPolytechnicalUniversity, 2009 (inChinese)

[7]肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993: 78-84

XiaoYelou,JinChangjiang.FlightTheoryofAtmosphericDisturbance[M].Beijing,NationalDefenseIndustryPress, 1993: 78-84 (inChinese)

[8]刘国福. 基于滑移率的车辆防抱死制动系统研究[D]. 长沙: 国防科学技术大学, 2007

LiuGuofu.AnInvestigationofVehicleAnti-LockBrakingSystemBasedOnSlip-Ratio[D].Changsha,NationalUniversityofDefenseTechnology, 2007 (inChinese)

[9]韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2009: 183-280

HanJinqing.ActiveDisturbanceRejectionControlTechnique[M].Beijing,NationalDefenseIndustryPress, 2009: 183-280 (inChinese)

[10] 黄一, 韩京清. 非线性连续二阶扩张状态观测器的分析与设计[J]. 科学通报, 2000, 45(13): 1373-1379

HuangYi,HanJinqing.AnalysisandDesignforSecondOrderNonlinearContinuousExtendedStatesObserver[J].ChineseScienceBulletin, 2000, 45(13): 1373-1379 (inChinese)

[11] 史静平. 先进飞机多操纵面控制分配方法研究[D]. 西安: 西北工业大学, 2009

ShiJingping.ResearchonControlAllocationMethodsinTheAdvancedAircraft[D].Xi′an,NorthwesternPolytechnicalUniversity, 2009 (inChinese)

Lateral Deviation Correction Control for Flying-Wing UAV Taxiing

Wang Yanxiong1, Zhou Zhou2, Shao Zhuang1, Zhu Xiaoping3

1.National Key Laboratory of Special and Technology on UAV, Northwestern Polytechnical University, Xi′an 710065, China 2.College of Aeronautics, Northwestern Polytechnical University, Xi′an 710065, China 3.UAV Research Institute , Northwestern Polytechnical University, Xi′an 710065, China

Abstract:Due to good robustness requirement of the control law, and the nonlinearity of six degrees-of-freedom multivariable mathematical model of flying-wing UAV, a nonlinear lateral deviation correction control law based on active disturbance rejection control technique (ADRC) for UAV is proposed. A complex control scheme include front-wheel steering, drag rudder and main-wheel differential braking is used. Due to the efficiencies of lateral deviation correction control actuators vary in a large range during taxing, and drag rudder and braking having ability of both lateral deviation correction and speed reduction, weighted pseudo-inverse method is used to allot yaw moment order and drag order. Antiskid brake control law based on ADRC is designed. The simulated result show that lateral deviation correction control law based on ADRC could estimates and compensates the adverse impact of runway environment and crosswind disturbance. Weighted pseudo-inverse method could allot yaw moment order and drag order dynamically.

Keywords:angular velocity; disturbance rejection; unmanned aerial vehicle; flying-wing; lateral deviation correction control; active disturbance rejection control; pseudo-inverse method; complex control

收稿日期：2015-09-22

作者简介：王彦雄(1989—)，西北工业大学博士研究生，主要从事飞翼布局无人机起降控制研究。

中图分类号：V249

文献标志码：A

文章编号:1000-2758(2016)04-0593-09