基于空域相关去噪法在电机故障信号上的应用研究

李　贝

(山西省振东实业有限公司，山西 长治 046000)



基于空域相关去噪法在电机故障信号上的应用研究

李贝

(山西省振东实业有限公司，山西 长治 046000)

摘要：近年来以新兴的Hilbert-Huang变换(HHT)为核心的衍生技术已经应用到了各个工程领域，特别在做信号特征提取方面颇显优势。然而，HHT也有其自身的不足，这为其今后的发展设立了障碍。为了使其应用领域更为广阔，不少学者对HHT的缺陷进行了深入研究。本文提出了利用滤波稳定性较好的小波空域相关法对电机故障信号进行去噪处理，这样可以较好地保留故障信号中的边缘信息，以此来削弱噪声对EMD分解质量的影响，最后求解基本模态分量的包络谱，试验结果证明了该方法的可行性。

关键词：希尔伯特-黄变换；小波空域相关去噪；小波包络谱；故障提取；齿轮故障

机械故障诊断经历了傅立叶分析、窗口傅立叶分析、维戈纳分析再到后来的小波分析。其中小波分析[1，2]是时频分析在信号提取、识别上应用较为广泛的，理论体系也比较成熟。然而，小波基一旦确定，信号的频率分辨率也确定了，这在实际信号的应用分析中有极大的局限性。对于上述的关键问题，1998年美籍华人黄鄂提出了希尔伯特-黄变换(HHT)，该方法已经应用到了电机故障诊断领域，并且在处理某些故障时有良好的结果。在使用这种方法做故障提取时大多都忽略了信号中的噪声影响，然而在对实际信号中，噪声的存在是必然的，这势必将会对分析结果产生影响，这时的IMF分量已经不能完全地反映真正的物理过程。因为含噪信号的EMD分解结果中很难分析出高频信号的包络，这使得低层的IMF分量变得研究意义不大。本文采用了通过对信号进行小波空域相关法降噪处理，以往这种方法多用于图像、语音信号的处理上[3]，本文将其移置到处理故障信号上来，并且通过大量的数据分析证明了这样的处理可以提高信号特征提取的精度。

1经验模态分解(EMD)

EMD分解的目的是将非线性信号根据局部时间特征(连续两个极值点的时间长度)，按照频率的高低分解成有限个IMF之和，这里的IMF是窄带信号，满足了Hilbert变换的要求。对于信号X(t)，EMD分解算法为：

1) 找到X(t)所有的局部极值点。

2) 对极大值和极小值，利用样条插值的方法建立信号的极大值包络函数和极小值包络函数，并记为E1和E2。

3) 计算上包络函数和下包络函数的均值m1。

4) 计算信号X(t)与包络均值函数m1的差值函数h1=X(t)-m1。

5) 重复上述的过程，将h1看成待处理的数据，于是有：h11=h1-m11。

6) 再重复上述的过程k次，直到有h1k=c1，即h1k是第一个经验模态函数分量，则c1就是从原始信号中得到的第一个经验模态函数。

7) 从原始信号X(t)中将c1剔除后，即r1=X(t)-c1，再对r1继续重复从i到Ⅵ的过程可以得到：

r1-c2=r2，…，rn-1-cn=rn.

(1)

直到最终的结果rn符合停止准则，即rn为一单调函数。于是原信号可以表示成：

(2)

2小波空域相关法

空域相关主要是利用了小波变换后，各小波系数在各尺度上有较强的相关性，特别是在信号边缘附近的相关性更明显，而噪声的小波系数却没有这种相关性。由于空域相关去噪法是基于小波变换后各个尺度上小波系数的相关性去噪的，因此又称作尺度相关性去噪，简称SSNF(Spatially Selective Noise Filtration)方法。改进后的小波空域相关的具体算法为：

1) 对含噪信号进行小波变换，得到Wf(j,n)，Wf(j,n)表示尺度j上，位置在n点处的离散小波变换。

2) 求出各个尺度与相邻尺度的Corr2(j,n)定义相邻尺度的相关Corrl：

(3)

一般l=2，有：

Corr2(j,n)=Wf(j,n)Wf(j+1,n) .

(4)

上式表示在j尺度上点n处的相关系数。

3) 将Corr2(j,n)进行能量归一化处理，得到新的相关值NewCorr2(j,n)。

(5)

式中n=1,2,…,N。

4) 估计j=1尺度上的噪声方差，由(5)式中的j=1时可以得到：

(6)

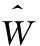
(7)

式中g是小波滤波器G第一尺度的单位脉冲响应，k为置零点数，N为信号长度。

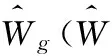
6) 重复步骤3)，5)，直到Pw(j)满足某一能量门限，即

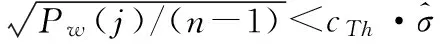
(8)

3仿真

实验信号选用频率是70 Hz的正弦信号对500 Hz的正弦信号进行频率调制，其中混有幅度为0.5的高斯白噪声，采样频率为1024 Hz， 采样点数为512，如图1所示。

图1　仿真信号

若不进行去噪，将原信号直接进行EMD分解，如图2所示。从IMF1中可以看出调频现象严重，并且其中混有噪声。使用本文的方法，先利用空域相关滤波将信号进行预处理，EMD分解层数明显减少，如图3所示。去噪后对第一个IMF做小波分解后的包络谱如图4所示，从图中可以看出70 Hz的调频信号清晰可见。

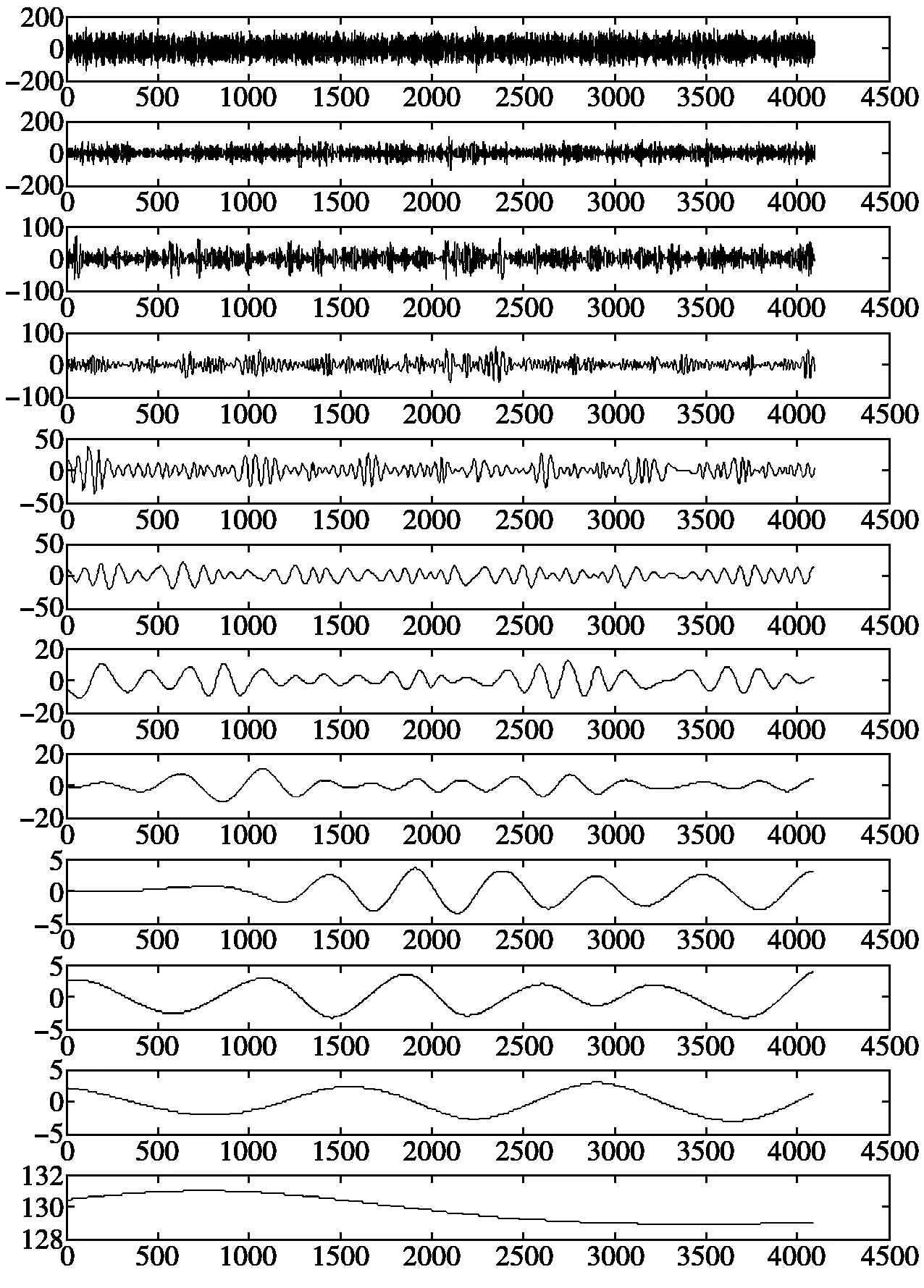
图2　去噪前EMD结果

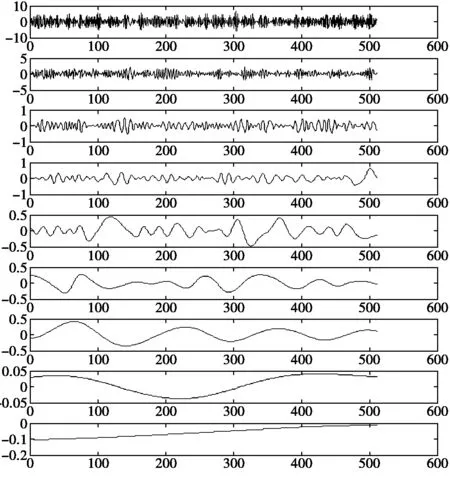
图3　去噪后EMD结果

图4　包络谱

4齿轮故障实例分析

数据来源：美国凯斯西储大学网站数据，轴承故障的直径为0.007英寸，在无负载情况下，转子速度是每分钟1 797转，采样频率为12 000 Hz，点数为2 048，经计算可得，无负载内圈故障频率为162 Hz。内圈故障的时域如图5，使用传统的EMD方法分解后，层数较多且后三层的IMF是没有意义的，只是在第一层IMF中有严重的调频调幅现象，并伴有明显的冲击，但是很难识别出故障频率。

图5　时域故障信号

使用本文方法，提取第一层IMF做小波分析，其包络谱如图6所示。

图6　第一层细节系数的包络

从图6中可以看出，161.1 Hz的谱线清晰可见。表1列出了在负载为1，2，3时(理论计算的故障频率分别是159.8 Hz，157.9 Hz和156.1Hz)使用本文方法提取轴承内圈故障的情况。

表1　使用本文方法提取内圈故障频率

3结论

从仿真试验中可以看出含噪信号在进行EMD分解时有多余的IMF分量存在，这说明噪声对EMD分解质量有很大的影响，并且发现随着层数的增加高频噪声的影响在减弱。在第一层IMF中调频调幅现象严重，这说明在原始信号含有丰富的高频分量。在研究去除高频分量的影响上，本文借鉴了处理语音、图像信号的经验,使用了空域相关法先对信号进行预处理，然后再EMD分解，再对分解得到的IMF做小波分析，得到小波包络谱。仿真及实例表明该方法可以较好地提出齿轮外圈故障频率，处理误差达到1%，满足工程需要，证明了方法的可行性。

参考文献

[1]Ling Jing,Qu Liang Sheng.Feature Extraction Based on Morlet Wavelet and Its Application for Mechanical Flaut Diagnosis[J].Journal of Sound and Vibration,2000,234(1):135-148.

[2]Peter W T,Peng Y H,Richard Y.Wavelet Analysis and Envelop Detection for Rolling Element Bearing Flaut Diagnosis-Their Effectiveand Flexibilities[J].Journal of Vibration and Acoustics,2000,123(3):303-310.

[3]孟晋丽，潘泉，张洪才.基于空域相关的小波域硬阈值滤波[J].2004(27):29-31.

[4]Huang N E,Shen Z,Long S R.The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J].Proc R Soc Lon A,1998(454):903-905.

[5]Huang N E,Shen Z,Long Steven R.A New View of Non-linear Water Waves:the Hilbert Spectrum[J].Annual Reviewof Fluid Mechanics,1999:417-457.

收稿日期：2016-01-12

作者简介：李贝(1989- )，男，山西长治人，硕士研究生，研究方向为计算机信息应用及信号与信息处理。

文章编号：1674- 4578(2016)02- 0038- 03

中图分类号：TP273.5；TN911.7

文献标识码：A

The Study and Application of Fault Extraction Based on the Time-frequency Analysis

Li Bei

(ShanxiZhendongCooperatesGroup,ChangzhiShanxi046000,China)

Abstract:Recently, some of derivative technology based on Hilbert-Huang transform (HHT) has been widely used in various engineering fields. Particularly, it has the significant advantage in the area of signal feature extraction. However, HHT also has its own shortcomings, which sets up the obstacles for its future development. In order to enable the wide application of HHT, so many scholars conduct an in-depth study in HHT’s Defects. For this purpose, the article uses the method of wavelet spatial correlation that with stable filtering to make denoising processes for motor fault signal, which can be better to retain the edge of the fault signal, and then, the signal after denoising makes empirical mode decomposition; the wavelet envelope spectrum of EMD named intrinsic mode function are extracted. The test shows that this method can extract fault single.

Key words:Hilbert-Huang transform; spatial correlation of wavelet denoising; wavelet envelope spectrum; fault extraction; gear fault