切换断路时间对非线性切换系统振荡特性的影响

陈章耀,王亚茗

(江苏大学 土木工程与力学学院，江苏 镇江 212013)



切换断路时间对非线性切换系统振荡特性的影响

陈章耀,王亚茗

(江苏大学 土木工程与力学学院，江苏 镇江 212013)

摘要：针对切换断路时间对非线性切换系统影响的问题，构建了非线性混合切换系统数学模型，并以广义Bohöffer-Vander Pol(BVP)切换电路为例，进一步画出了不同切换断路时间的切换系统分岔图。对分岔图的分析表明：切换断路时间对切换系统的各种振荡行为如混沌解和周期解等会产生不同程度的影响。另外，考虑切换断路时间情况下，切换系统还会产生一种特殊的倍周期分岔行为。

关键词：非线性动力系统；混合切换；切换断路时间；广义BVP系统

0引言

切换是工程中常见的控制方法，如电网控制[1]、飞行器导航[2]和汽车换挡[3]等都有切换系统的应用。其中，线性切换系统已有很多研究[4-5]，而非线性系统由于较为复杂，研究还相对较少。在非线性动力学领域，学者们已经构建了大量描述自然规律和工程现象的非线性系统模型，如Chua式电路[6]和Duffing方程[7]等，这些系统加入切换条件后会产生更为复杂的现象，因此，需要深入探讨具体切换系统的动力学演化过程，进而揭示其本质。

非线性切换系统按切换规则可以分为时间切换、状态切换和混合切换。关于时间切换系统的研究较多[8-10]，而状态切换和混合切换系统的相关研究则相对较少[11-12]，并且这些研究所用的模型都较为理想化，即在满足切换条件的时刻，切换系统瞬间从一个子系统切换到另一个子系统。在实际应用中，切换系统从一个子系统断开，切换到另一个子系统，会产生一段切换断路时间，关于该因素对切换系统造成的影响还鲜有报道。因此,本文以广义Bohöffer-Vander Pol(BVP)电路[13]为例，通过设置依赖于状态的切换条件，并考虑切换断路时间对切换系统的影响，研究具有复杂振荡行为的非线性切换系统，以期为实际应用提供理论依据。

1切换系统数学模型的建立

本文的切换断路时间是指切换系统在子系统之间切换时，由于切换装置的物理结构，从一个子系统切换到另一个子系统过程中，必然有一段切换所需要的时间，该段时间不受两个非线性子系统控制。而在该段时间内，电路会形成一个新的线性系统，把这个新的系统也看成一个子系统。考虑切换断路时新的线性子系统，切换系统一共有3个子系统，实质上是一个时间和状态的混合切换系统。其数学模型通常可简写为：

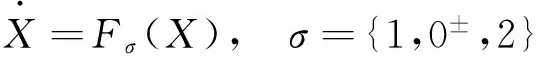
(1)

其中：X={x,y,z}T；Fσ为相应的子系统；σ表示相应的切换规律，数学定义为：

其中：τ0为切换断路时间;σ=1为切换系统受子系统1控制;σ=2为切换系统受子系统2控制；σ=0+为从子系统1切换到子系统2的中间过程；σ=0-为从子系统2切换到子系统1的中间过程；X=X01和X=X02为相应子系统的状态切换面，用∑1和∑2表示。这样就把切换断路问题转化成3个子系统的混合切换问题，通过调整切换断路时间T的值，来研究其对整个系统的影响。

模型(1)是广义的切换系统模型，具有概括性。为了分析更为具体的切换系统振荡行为，本文用一个具有复杂动力学行为的广义BVP振荡模型，通过一个双向开关构建了一个非线性切换电路系统，如图1所示。之所以引入电路系统，是因为实际中很多动力学模型的运动情况都可以通过传感器转化为电路信号，通过构建与实际数学模型对应的电路系统，就可以完全模拟实际振荡情况，大大方便对实际系统的分析。

图1　广义BVP切换电路

该电路系统由一个线性电阻r、两个电容C、一个电感L和两个不同的非线性电阻R1、R2组成。开关S随电压v1的不同,会在SW1和SW2之间切换。其切换规律为：假设开关位于SW1，在系统振荡过程中电压v1的值达到v1=vS2时，开关S离开SW1，并消耗时间T切换到SW2；当系统振荡过程中v1的值达到v1=vS1时，开关S离开SW2，消耗时间T回到SW1。当开关在SW1或SW2端时，均为一广义BVP系统，只是非线性电阻不同；当开关处于SW1和SW2之间，失去非线性电阻的线性电路构成子系统0。系统状态可以由如下方程描述：

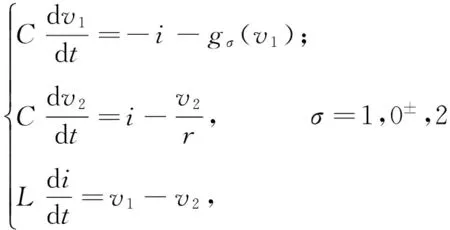
(2)其中：σ每取一个值，就对应一个方程组，σ=1时，开关S位于SW1，系统受子系统1控制；σ=2时，开关S位于SW2，系统受子系统2控制；σ=0±时，系统处于切换过程中，受新的线性子系统0控制。gσ(v1)=-aσv1-bσtanh(cσv1)表示非线性电阻的电压和电流特性，aσ、bσ和cσ为常数(σ=1,0±,2)，σ=0±时，a0=b0=0，即g0(v1)=0。

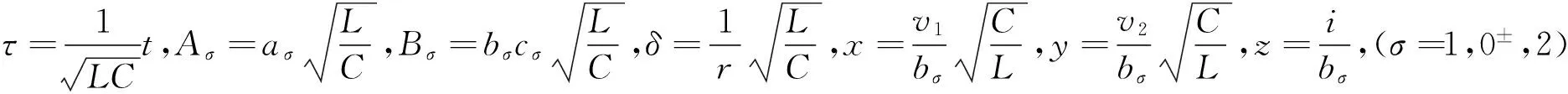
(3)

其中：x,y,z分别为图1中广义BVP切换电路的电压v1、v2和电流i无量纲化后的未知变量;Aσ、Bσ和δ都是和电路中电容电感相关的参数，当σ=0±时，A0=B0=0。由于式(3)中的所有变量和参数都是无因次量，因此没有单位。

2切换断路时间对切换系统振荡特性的影响

只要存在切换断路时间T，肯定会对切换系统造成影响，T越大对系统的影响也越大，T趋向于0时对系统影响最小。当T增大到一定程度，轨线会脱离切换条件控制落入子系统的其他吸引域，因此，本文选取一个尽量大但又不会使轨线脱离切换条件控制的T值范围进行研究，以便观察其对切换系统的影响。这里选0≤T≤0.22，并且令A1=B1=0.7，A2=B2=q，取状态切换面∑1∶x=0,∑2∶x=2，初始值为(0,0.665,0.124)，分别画出不考虑切换断路时间的理想状态和考虑切换断路时间的切换系统随q变化的分岔图，用以比较其振荡行为的差异。

在比较差异之前，首先简要说明该切换系统的运动规律。取q=0.67,T=0.22，对考虑切换断路时间的切换系统轨线路径进行分析，其相图和时间历程图如图2所示。从图2a中可以明显看出：这是一个周期一振荡，可以分为AB、BC、CD和DA这4个部分。首先，假设初始点为A，切换系统受子系统1控制沿图2a中箭头方向的粗实线运动。当运动到切换面∑2上的B点，满足切换条件发生切换，切换后开关需要时间T=0.22才能到达子系统2，在这段时间里轨线受新形成的子系统0控制沿细线BC运动。当经过时间0.22后轨线到达C点，开关切换到子系统2，因此，轨线受子系统2控制沿实线CD运动。当运动到切换面∑1上的D点，又满足切换条件产生切换，而切换过程同样需要时间T=0.22才能到达系统1，这段时间内同样受子系统0控制沿细线DA运动。最后经过时间T=0.22回到A点形成一个周期一振荡。从图2b中可以很清楚地看出q=0.67,T=0.22时切换系统在x方向随着时间变化的振荡行为，其中，A点、B点、C点和D点与图2a中的点相对应。

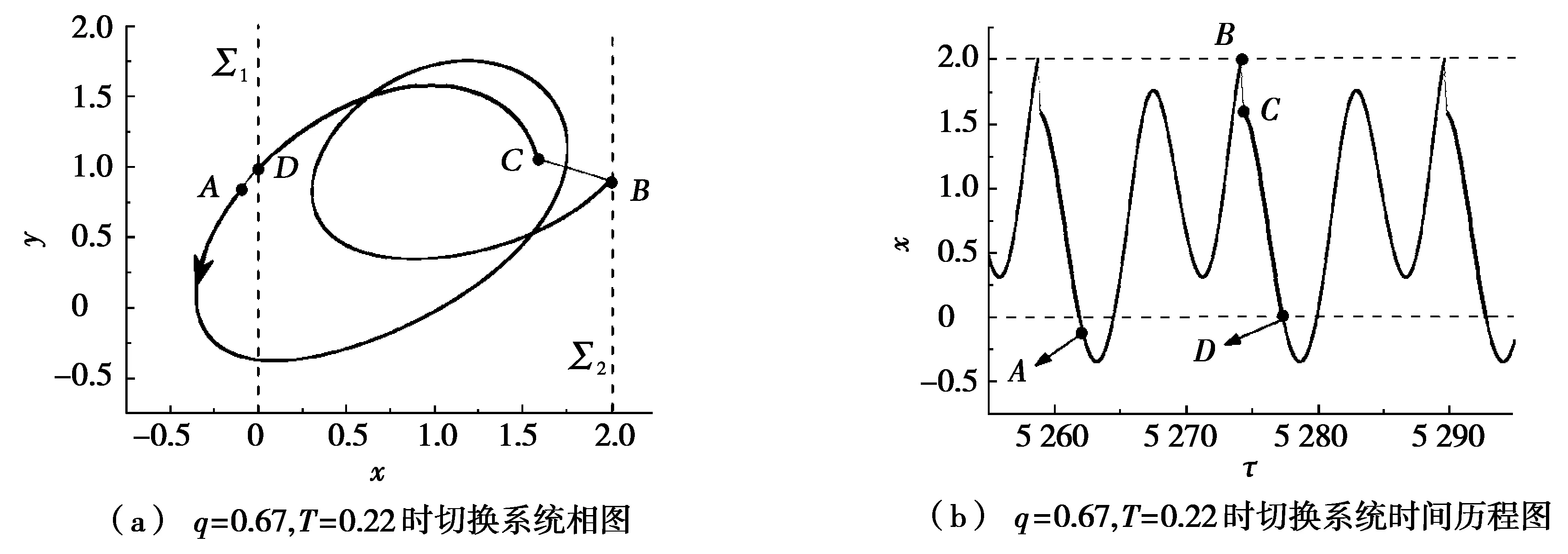
图2　q=0.67,T=0.22时切换系统振荡机理图

通常，画出切换系统随参数q变化的分岔图可以很好地表现其分岔特性，因此,取不同的切换断路时间T的值，画出切换系统随参数q变化的分岔图，并对这些图进行比较，观察不同的时间T对切换系统分岔图的影响，以便发现其规律。其中，分别取T=0和T=0.22，以∑1为Poincaré截面，画出参数q∈(0.664,0.900)切换系统的分岔图,如图3所示。

图3　不同切换断路时间T时切换系统随参数q变化的分岔图

由图3可以看出：随着T的增大，切换系统的动力学行为有很大改变。首先，不考虑切换时间的切换系统分岔图中参数为(0.775,0.894)的混沌区域，在考虑切换时间后随着时间的增大，大部分参数范围都变为周期振荡，局部参数范围还会产生新的混沌现象。另外，在图3a中，参数为q∈(0.664,0.775)的周期解区域，随着T的增大，大部分参数范围都变为混沌区域，少部分区域周期解的结构发生了改变。在不考虑切换时间时出现的如图3a周期解区域的周期突变现象，随着时间T的增大，会逐渐消失，在图3b中已经几乎看不到周期突变现象。

3切换断路导致新的分岔行为

图4　　　　T=0.22时切换系统在参数q为　　　(0.702 0,0.714 0)时的分岔图

当切换断路时间T增大到一定程度，如当T=0.22，还会产生一种特殊的倍周期分岔行为，图4为图3b在参数q为(0.702 0,0.714 0)的放大图，通过图4可以看出其分岔过程。

通常倍周期分岔都对应着通往混沌的路径，而在图4中，随着参数的变大，在参数q(0.703 7,0.707 7)时切换系统发生2次倍周期分岔，即从周期二解分岔为周期四解，又从周期四解分岔为周期八解。但是，该过程并没有形成概周期解或者通往混沌，而是又转化为周期四解。这里的倍周期分岔指的是相应切换面上切换点数目的成倍增长，其成倍增长的过程构成了其分岔序列。图5a和图5b分别是q=0.704 0和q=0.706 0时切换系统的相图，通过比较可以明显发现：图5b的周期数要比图5a的周期数多，在图5a中切换系统存在一个周期二解，其对应的每个子系统控制的轨线都存在两种运动，两种不同的运动循环构成了一个周期二解。在图5b中，切换系统存在一个周期八解，可以发现其振荡行为已经类似混沌，但还是周期解，随着参数的变大并没有变为混沌。

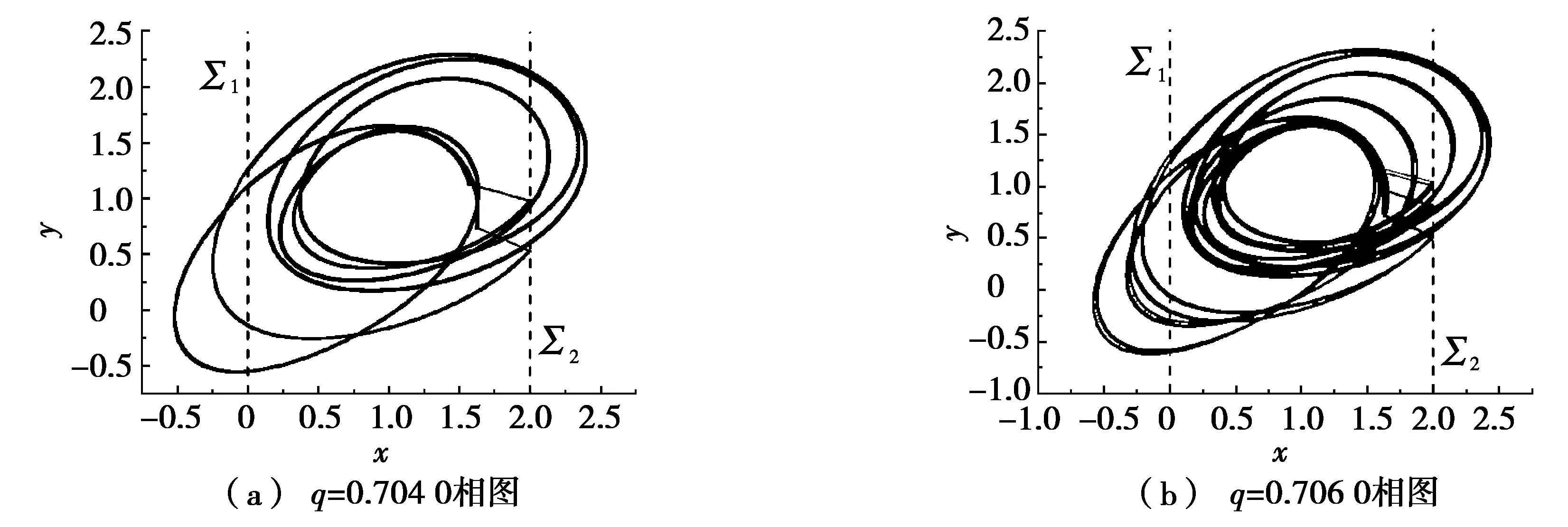
图5　T=0.22时切换系统的特殊倍周期分岔过程

4结论

考虑切换断路时间的状态切换系统，实质上是一个有3个子系统的时间状态混合切换系统。考虑切换断路时间后，随着断路时间T的变大，在相同参数和初始值下，原状态切换系统的混沌解会转化成周期解和不同类型的混沌解，而周期解的结构也会逐渐发生变化，并可能演化成混沌解。因此，实际应用中应综合考虑切换系统的动力学特性，把切换断路时间控制在一个合理的值。最后，考虑切换断路时间的切换系统还会产生与原切换系统不同的分岔行为，主要体现在倍周期分岔并没有通向混沌。

参考文献：

[1]王红燕,闫瑞杰.微电网并网和孤岛运行的无缝切换控制策略[J].河南科技大学学报(自然科学版),2014,35(5):50-54.

[2]OISHI M,MITCHELL I,BAYEN A M,et al.Hybrid verification of an interface for an automatic landing[C]//Decision and Control,Proceeding of the 41st IEEE.Las Vegas,Nevada USA,2002:1607-1613.

[3]BALLUCHI A,BENEDETTO M D D,PINELLO C,et al.Hybrid control in automotive application:the cut-off control[J].Automatica,1999,35(3):519-535.

[4]陆慧玲,李绍龙,张正娣.参数激励下分段线性两尺度系统的分岔[J].河南科技大学学报(自然科学版),2015,36(6):71-74.

[5]刘洪刚,付主木,高爱云.不确定切换时滞线性系统的状态反馈鲁棒H∞控制[J].河南科技大学学报(自然科学版),2008,29(4):69-72.

[6]陆安山,陆益民.忆阻蔡氏对偶混沌电路分析[J].河南科技大学学报(自然科学版),2015,36(2):92-95.

[7]李爽,李倩,李佼瑞.Duffing系统随机相位抑制混沌与随机共振并存现象的机理研究[J].物理学报,2015,64(10):1-7.

[8]CHEN Z Y,XUE Z H,ZHANG C,et al.Oscillation behaviors and mechanism of Rayleigh oscillator with periodic switches[J].Acta physica sinica,2014,63(1):1-8.

[9]LI H X,ZHANG C,YU Y,et al.Periodic switching oscillation and mechanism in a periodically switched BZ reaction[J].Science China,2012,55(10):2820-2828.

[10]GAO C,BI Q S,ZHANG Z D.The oscillation and bifurcation of a switching system composed of jump circuits[J].Acta physica sinica,2012,62(2):1-8.

[11]KOUSAKA T,UETA T,KAWAKAMI H.Bifurcation of switched nonlinear dynamical systems[J].IEEE transactions on circuits and systems,1999,46(7):878-885.

[12]张春.非线性切换系统的复杂动力学及其机理研究[D].镇江:江苏大学,2014.

[13]NISHIUCHI Y,UETA T,KAWAKAMI H.Stable torus and its bifurcation phenomena in a simple three-dimensional autonomous circuit[J].Chaos,solitons & fractals,2006,27(4):941-951.

基金项目：国家自然科学基金项目(11472115,11572141,11502091);镇江市科技攻关基金项目(GY2013032,GY2013052)

作者简介：陈章耀(1960-),男,江苏镇江人,副教授,博士,硕士生导师,主要从事非线性动力学方面的研究.

收稿日期：2016-03-08

文章编号：1672-6871(2016)05-0087-04

DOI:10.15926/j.cnki.issn1672-6871.2016.05.019

中图分类号：O322

文献标志码：A