基于D-S理论的多模型凝析气井流量算法研究

王艳芝，吴海浩，宫　敬

(中国石油大学(北京)油气管道输送安全国家工程实验室/城市油气输配技术北京市重点实验室，北京 102249)



基于D-S理论的多模型凝析气井流量算法研究

王艳芝，吴海浩，宫敬

(中国石油大学(北京)油气管道输送安全国家工程实验室/城市油气输配技术北京市重点实验室，北京 102249)

摘要：随着海洋油气开发走向深海，虚拟流量计逐渐成为水下油气井产量计量的一种重要方式，其核心是流量计算模型。介绍了虚拟流量计的井筒和油嘴模型，并基于跨接管的流动特点建立了跨接管流量计算模型。根据D-S证据理论建立了各流量模型的权重提取模型，并利用Dempster法则对各模型权重进行融合处理，最终得到基于D-S理论的凝析气井流量融合计算模型。结果表明，该融合模型在整体上有效提高了流量计算的精度和可靠性，且对短时间内的流量变化具有较好的预测能力，为水下虚拟流量计的研发提供了一种新的思路和方法。

关键词：D-S理论；气井；多模型；流量计算；虚拟流量计

随着我国海洋油气工业向深水进军，伴随其的水下生产系统应用也越来越多，由于传统水下多相仪表安装成本高，日常的校准和维护困难而使得水下油气井的产量计量成为难题。20世纪90年代初，虚拟流量计系统(Virtual Metering System，VMS)首次应用于油气田开发技术中[1]，该系统以管道沿线的各传感器采集的数据为基础，通过多模型组合计算得出各个井口的产量、含水率等生产参数，实现对系统生产虚拟计量的目的。虚拟流量计系统的核心是基于多模型的流量计算模块，其决定整个计量系统的精度。D-S证据理论中的Dempster组合规则能够对多个证据体进行融合得到一个新的证据体，即利用组合规则重新对各个证据源进行信度分配得到一个新的可信度分配，其能够反映出各信息源之间的联合作用，故可以将D-S理论应用在多模型的融合算法中。笔者对凝析气井单井流量计算的井筒模型和油嘴模型进行研究，并在其基础之上新建立和验证跨接管流量计算模型，此外，还主要针对单一流量计算模型在某些情况下由于其自身局限性计算偏差过大的情况，将D-S理论引入到虚拟流量计的多模型计算中，利用Dempster合成法则对3种模型的计算结果进行融合处理，得到单个模型在多模型融合计算中的权重，通过多模型数据融合削弱了单个模型自身局限性对计算结果的影响，可有效提高虚拟流量计的精度、稳定性及可靠性。

1流量计算模型

较为典型的水下气田流动系统如图1所示。

根据节点分析原理，从井底至采油平台的流动存在多种流动形式：井筒、油嘴及跨接管中的多相流动[2]。虚拟流量计技术中的单井流量计算模型正是依据上述流动过程建立的，主要包括井筒模型、油嘴模型及跨接管模型。

1.1井筒模型

对于井筒流量计算模型，首先估计该凝析气井的大致产量，然后基于该流动过程建立能量平衡方程和连续性方程来描述井筒的稳态流动，最后根据井筒的稳态流动算法及井筒两端的压力和温度迭代求解出单井流量[3-4]。

1.2油嘴模型

油嘴模型进行过油嘴多相流体质量流量计算源于20世纪90年代，早期的模型多为经验相关式模型，适用范围较窄，常用的经验相关式模型主要有Fortunati相关式模型[5]、Gilbert相关式模型[6]、Ashford-Pierce模型[7]等。目前，工业应用的模型多是半经验的理论模型，此类模型将实验与理论推导有机结合，在动量及能量守恒方程的基础上引入合理假设得到更具一般性的模型，如Sachdeva模型[8]、Perkins模型[9]、Hydro模型[10]等。在油嘴模型的实际运用中，由于各油气田产物和生产系统的特点不同，需要选用相对应的油嘴模型进行质量流量预测。此外，各油嘴模型在现场的实际运用环境和实验室建模时的条件会有一定程度差异，所以模型在使用时需要进行计算参数的变换和修正[11]。这里主要采用基于相关参数修正后的Sachdeva和Perkins 2种模型来进行油嘴质量流量的计算及预测。

1.3跨接管模型

增加流量计算模型可在一定程度上提高虚拟流量计的精度和可靠性。因此，在井筒和油嘴模型的基础之上，根据跨接管的特点和介质流动过程建立跨接管流量计算模型。从图1可知，跨接管为油嘴后与管汇间的一段管道，其大部分放置在海底，少部分管道因连接管汇而浸泡在海水中。其特点为长度短，压降小，在没有保温层的情况下温降会很大。随着跨接管在海底运行一段时间后，管道表面会被泥沙覆盖而对其传热造成很大的影响，因此需定期对其传热系数进行校正。

根据跨接管的特点并结合工程实际应用，忽略跨接管的压降，故仅需根据跨接管的热力计算来建立跨接管流量计算模型。这里跨接管的温降计算采用邓道明等[12]推导的天然气—凝析液混输管线温降计算公式:

(1)

在管段基础参数已知及忽略压降的情况下，将式(1)抽象为函数：

(2)

由管汇处的能量守恒可得：

(3)

给定每根跨接管1个流量的初始值及管汇处的温度值，流量的初始值根据井筒模型、油嘴模型或经验值确定，通过求解上述非线性方程即可得到每根跨接管的质量流量。

2D-S证据理论

2.1基本概念

证据理论(D-S理论)由A.P.Dempster和其学生G.Shafer共同创立[13]。由于D-S理论不受先验信息等因素的制约，故其可以通过和其他理论方法相结合来解决实际问题。

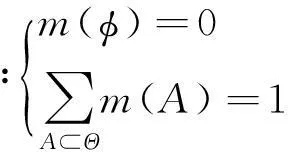
2.2Dempster合成法则

D-S证据理论的核心内容就是Dempster合成法则，通过合成法则可以把各信息源的证据的联合作用结果定量计算出来，最终得到联合作用下的决策[14]。

2个信度函数的Dempster合成法则：设Bel1、Bel2是同一识别框架Θ上的2个独立的信任函数，m1、m2是他们各自的BPA函数，焦元分别为A1，A2，…，Ak和B1，B2，…，Bk。由合成法则可求得新的概率分配函数：

(4)

多个信度函数的合成法则和2个信度函数的合成法则类似。

3基于D-S理论的数据融合模型

3.1基于Dempster合成法则流量融合模型的建立

基于Dempster合成法则的凝析气井流量计算融合模型的建立过程如图2所示。

融合模型建立过程为：

(1)根据管道沿线的温度、压力等基础数据，分别用井筒、油嘴、跨接管3种流量模型进行计算，通过各模型计算结果的相对误差计算出各模型所对应的权重f。

(2)将一段时间内各模型所占的权重数据按照Dempster合成法则进行融合，得到该段时间内流量样本数据的融合权重(f1，f2，f3)。

(3)应用融合权重对所测试时间段内3种流量模型的计算结果进行融合处理：W=f1W1+f2W2+f3W3，从而得到最终的计算结果。

3.2基于D-S理论的融合权重模型

3.2.1权重提取模型

在运用Dempster合成法则对权重融合处理之前，首先需要建立权重提取的数学模型。对多模型组合技术权重的确定方法有很多种，按其计算方法的不同可分为最优组合权重和非最优组合权重确定方法。最优组合权重确定方法是根据某种准则构造关于权重的目标函数，在一定约束下求得目标函数的最大值或最小值，从而求得各个模型的权重，一般情况下计算量较大，不适合工程应用。非最优组合权重确定方法就是根据各个单项预测模型预测误差的方差和其权系数成反比的基本原理，给出组合预测的权系数的计算公式，简便可行，适合工程应用。常见的非最优组合权重确定方法主要包括算术平均法、方差倒数法、均方倒数法、简单加权法、标准差法、二项式系数法等[15]。文献[16]所述的几种非最优组合权重确定方法中，方差倒数法所得到的组合模型精度相对较高，因此，笔者采用方差倒数法来确定各模型的权重。

假设井筒、油嘴、跨接管3种模型在一段时间内对气井总流量的计算值分别是W1，W2，W3，气井总流量的真实值为W，3种模型的预测相对误差分别为e1，e2，e3，则多模型组合的计算结果为：

(5)

由方差倒数法可得各模型权重为

(6)

其中，Di为误差ei(i=1，2，3)的平方和。

3.2.2基于D-S理论的权重融合模型

式(5)的权重约束条件与D-S理论中基本概率分配所满足的条件相似，故可通过类比的思想利用Dempster合成法则对多组权重进行融合。

在识别框架θ={W1，W2，W3}上建立基本概率分配m，其对应的值分别为：

(7)

对所测试时间段内的各模型流量数据进行分组，根据每组数据得到一组权重，其所对应的基本概率分配值分别为mj(Wi)(i=1，2，3)，其对应的信度函数为Belj(j=1，2，…，n)，采用Dempster合成法则首先对前2组信度函数进行融合，将融合结果所对应的基本概率分配值记为m，其融合过程为：

(8)

其中，K=m1(P1)m2(P2)+m1(P1)m2(P3)+m1(P2)m2(P1)+m1(P2)m2(P3)+m1(P3)m2(P1)+m1(P3)m2(P2)之后，再将合成的信度函数依次与后面的信度函数进行融合，最终融合后的权重值为mc(W1)，mc(W2)，mc(W3)，从而得到数据融合模型的计算结果：

(9)

4实例计算及结果分析

收集了我国南海某水下气田2口采气井2014年2～3月的总生产流量数据和该水下气田流动管线的基础数据，为了简化计算，每1 d分别选取1组生产流量数据，2月份一共提取28组生产数据，如表1所示。分别应用上述3种流量模型对该气田的产气量进行计算，计算结果如图3所示。从图3中可以看出，油嘴模型的计算效果整体上最差，跨接管模型的计算精度仅次于井筒模型，但2者计算结果均较为接近实际工况，且能较好地适应工况发生变化时的情况。

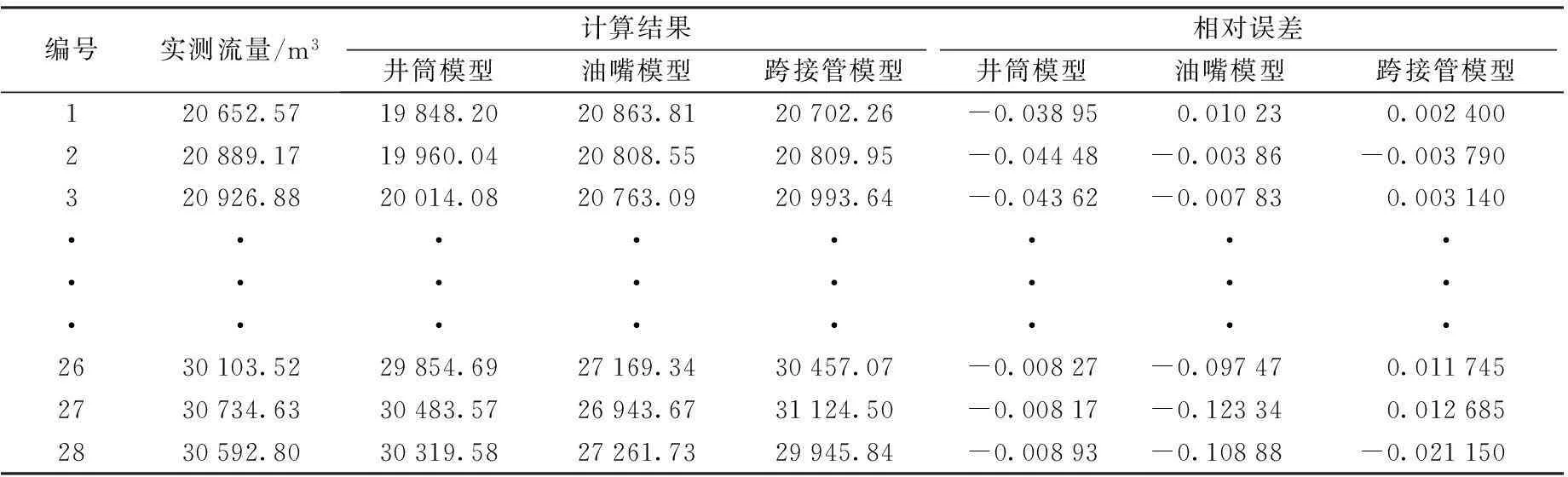
表1　各模型计算结果及误差

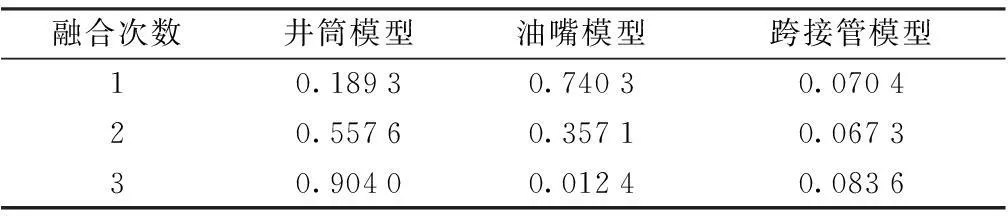
表2　权重逐重融合过程

利用D-S相关理论对3种模型的计算结果进行融合处理，其中每7组数据进行1次权重计算，得到4组权重，然后对权重进行融合计算，共进行3次融合，融合后的权重信息包含了当前所有数据点提供的权重信息，权重融合过程如表2所示。利用融合后的权重对各模型的计算结果进行数据融合，得到融合后及各单个模型的计算结果，如图3所示，平均绝对百分比误差(MAPE) 如图4所示。由图4中可看出，融合模型后的计算结果整体上优于单个模型的计算结果，且误差较小，平均绝对百分比误差仅为0.023，说明基于D-S理论的融合模型整体上提高了计算精度，使计算结果最大程度地接近误差最小的计算模型，且整体上又优于误差最小的模型，提高了整个虚拟流量计系统计算结果的可靠性，不会因某一模型的局部误差过大而影响系统的计算结果。

融合后的权重包含了当前1个月内数据对各单个模型计算准确性高低的信息，在实际工况不发生大的变化的情况下，应用该融合模型对未来短期内流量的变化具有较强的预测能力。应用上述融合权重建立融合流量模型对3月1～10日内流量变化进行预测，结果如图5所示，预测结果的平均绝对百分比误差如图6所示。从图5、图6中可以看出，在没有将这10 d的实测数据信息融合到权重信息中的情况下，融合模型的预测结果仍然较好，说明基于D-S理论的融合模型在短时间内具有较好的预测能力，在没有实测流量数据的情况下，可以为现场的生产提供一定的参考信息。如果后续的生产工况发生较大的变化，则需根据工况变化后各模型的计算数据及实测数据计算新的权重，并将新的权重信息和之前的融合权重进行融合，得到新的融合权重信息，然后再进行数据融合模型计算。

5结论

(1)给出了基于多相流动过程的水下凝析气井的井筒和油嘴流量模型，并针对水下生产装置跨接管的特点，建立了基于热力过程的跨接管流量计算模型。计算结果表明，跨接管模型的计算结果仅次于井筒模型，具有较高的准确性。

(2)介绍了D-S证据理论的基本原理和Dempster合成法则，并在此基础上提出了基于D-S理论的水下凝析气井多模型融合的流量计算方法。

(3)基于D-S理论的融合流量模型的计算结果整体上优于单个流量计算模型，可有效提高水下凝析气井流量计算的精度和可靠性，而且能较准确地预测未来一段时间内的流量变化，为水下虚拟流量计的研发提供了一种新的思路和方法。

参考文献

[1]Bergk Davalathj. Field Applications of I-dun Production Measurement System[C]. OTC 14007， 2002.

[2]张琪.采油工程原理与设计[M].山东:中国石油大学出版社，2006.

[3]王智，宫敬，尹铁男，等.天然气凝析液长距离管道稳态水力热力计算[J].东北石油大学学报，2013，37(4):60-66.

[4]王智.深海天然气集输系统在线模拟方法研究[D].北京:中国石油大学(北京)，2015．

[5]Fortunai F. Two-Phase Flow through Wellhead Chokes[C]. SPE European Spring Meeting， Amsterdam， Netherlands， May 16-18， 1972， SPE-3742.

[6]Gilbert W E. Flowing and Gas-Lift Well Performance[C]. Spring meeting of Pacific Coast District， Division of Production， Los Angeles， May 1954.

[7]Ashford F E， Pierce P E. Determining Multiphase Pressure Drops and Flow Capacities in Down-Hole Safety Valves[J]. J P T， 1975，27(9):1145-1152．

[8]Sachdeva R， Schmidt Z， Brill J P，et al. Two-Phase Flow Through Chokes[C]. SPE Annual Technical Conference and Exihibition， New Orleans， U.S.A， 1986， SPE-15657．

[9]Perkins T K. Critial and Subcritical Flow of Multiphase Mixtures through Chokes[J]. SPE Drilling & Completion， 1993，8(4):271-276．

[10]Slemer-Oslen S， Holm H， Haugen K，et al. Subsea Choke Flow Characteristics[C]. 7th International Conference on Multiphase Production Technology， Cannes， France， June 15-17， 1995．

[11]Schoppa W， Jayawardena S. Bonga-Flow Assurance Benchmarking via Field Surveillance[C]. Offshore Technology Conference held in Houston， Texas， USA.30 April-3 May， 2007．

[12]邓道明，宫敬.天然气-凝析液混输管线温降计算[J].工程热物理学报，2008，10(29):1691-1694．

[13]Dempster A P. Upper and lower probabilities induced by a multi-valued mapping[J]. The Annals of Mathematical Statistics， 1967，38(2):325-339.

[14]祝晓坤.Dempster-Shafer证据推理融合模型在遥感分类中的应用[D].武汉:武汉大学，2005.

[15]戴华娟.组合预测模型及其应用研究[D].长沙:中南大学，2007．

[16]毛开冀.关于组合预测中的权重确定及应用[D].成都:成都理工大学，2007.

Research on Flow Algorithm of Multi-Model Condensate Gas Wells Based on D-S Theory

WANG Yan-zhi, WU Hai-hao, GONG Jing

(National Engineering Laboratory for Pipeline Safety/Beijing Key Laboratory of Urban Oil and Gas Distribution Technology, China University of Petroleum-Beijing, Beijing 102249, China)

Abstract:With the development of offshore oil and gas into the deep sea, virtual flow meter has become an important measurement method of oil and gas well production, and the core algorithm is the flow calculation model. This paper introduced wellbore and nozzle flow calculation model of virtual flow metering system, and established the jumper flow calculation model based on the characteristics of cross pipe. This paper introduced D-S evidence theory, established the weight extraction model of multi-flow-model, employed Dempster’s rule to deal with the weight of each flow model, and finally attained the fusion flow calculation model of condensate gas wells. The results show that the fusion model can effectively improve the flow calculation accuracy and reliability on the whole, and predict the flow changes in the next period of time, which provides a new idea and method for the development of virtual flow meter.

Key words:D-S theory; condensate gas wells; multi-model; flow calculation; virtual flow meter

收稿日期:2016-02-25

基金项目：“十二五”国家科技重大专项(2011ZX05026-004-03)。

作者简介：王艳芝(1991—)，女，在读硕士，主要从事多相流及油气田集输技术方面的研究，E-mail：wangyanzhicup@163.com。

中图分类号：TE863

文献标志码：A