阴离子表面活性剂临界胶束浓度的QSPR研究

祁　凡，金　俏，张志红，何晓囡

(北京石油化工学院化学工程学院，北京 102617)



阴离子表面活性剂临界胶束浓度的QSPR研究

祁凡，金俏*，张志红，何晓囡

(北京石油化工学院化学工程学院，北京 102617)

摘要：以价分子连接指数(0χ，1χ，2χ)为自变量，临界胶束浓度(cmc)为因变量，采用QSPR方法和SPSS 21.0统计软件建立了样本数为40的数学模型。最佳模型为lg cmcobs=2.245-0.7252χ，复相关系数R2=0.864。从预测方程可看出临界胶束浓度与2χ呈负相关关系。筛选过程中发现，0χ，1χ与函数值之间线性关系微弱，与2χ共线性较强，确定了临界胶束浓度最重要影响因素为2阶价分子连接指数(2χ)。内部验证使用留一法(Leave-one-out)，得到的交叉验证系数q2=0.831，证明模型稳定性和预测性良好。残差频率分布直方图基本符合正态分布，实验预测值对比图中大部分样本点落在对角线附近，具有明显线性关系。从统计量及图表可证明，该方程可以用来预测阴离子表面活性剂的临界胶束浓度。

关键词：阴离子表面活性剂；QSPR；临界胶束浓度

表面活性剂是一种少量加入就能使溶液体系界面状态发生明显变化的物质，其分子由亲水基团和疏水基团组成，故在溶液表面能定向排列。表面活性剂溶解在溶液中于本体和表面层分布，其中部分分子排列在表面层，极大地减小了空气与溶液的接触面积，造成其表面张力的迅速衰减，当表面活性剂浓度升高到一定程度时，液面上形成一层一层定向排列的单分子膜，而在溶液本体中表面活性剂分子形成一定形状的胶束，开始形成胶束所需最低表面活性剂浓度称为临界胶束浓度(cmc)。表面活性剂能改变界面特性的这种性质使得其在环境、药物、化工领域都有广泛的应用[1-2]，而临界胶束浓度是其重要的特征数值之一。表面活性剂分为阴离子、阳离子、两性、非离子等，其中阴离子表面活性剂年产量和使用量相比其他种类表面活性剂大很多，对阴离子表面活性剂的QSPR研究近年也有一些进展，王正武等[3]对阴离子表面活性剂的临界胶束浓度建立了数学模型，但计算结果尚有欠缺。朱志臣等[4]对各类表面活性剂的临界胶束浓度的QSPR进行了研究，但是计算过程比较繁琐。

QSPR是由Hansch和Free-Wilson等[1]建立并发展的定量构效关系，该方法通过使用数学模型并用分子结构描述其性质，其基本假设是物质的某一性质P与描述符xi之间存在多元线性关系，其表达式为：

(1)

式中：a0为常数，ai为回归系数。

分子的结构、拓扑、电性、几何描述符，量子化学描述符和热力学描述符为描述符的3个大类，目前QSPR描述符数量已经达到数百种。

1数据来源

以40个硫酸盐和磺酸盐阴离子表面活性剂为样本，其lgcmcobs值见文献[5]，因cmc随温度和含盐量变化数据缺乏，故采用40 ℃下纯水中cmc值进行建模，cmc数值如表1所示。

2QSPR模型建立

2.1价分子连接指数

将被讨论的表面活性剂分子进行碎片化，得到点、一阶路径、二阶路径等碎片。每个原子都可以由其电子排布计算出价点价，将价点价进行累乘和累加运算可以求得该分子的各阶价分子连接指数。价点价和价分子连接指数公式为：

(2)

(3)

计算样本中40个阴离子表面活性剂的0χ，1χ，2χ，数据如表1所示。

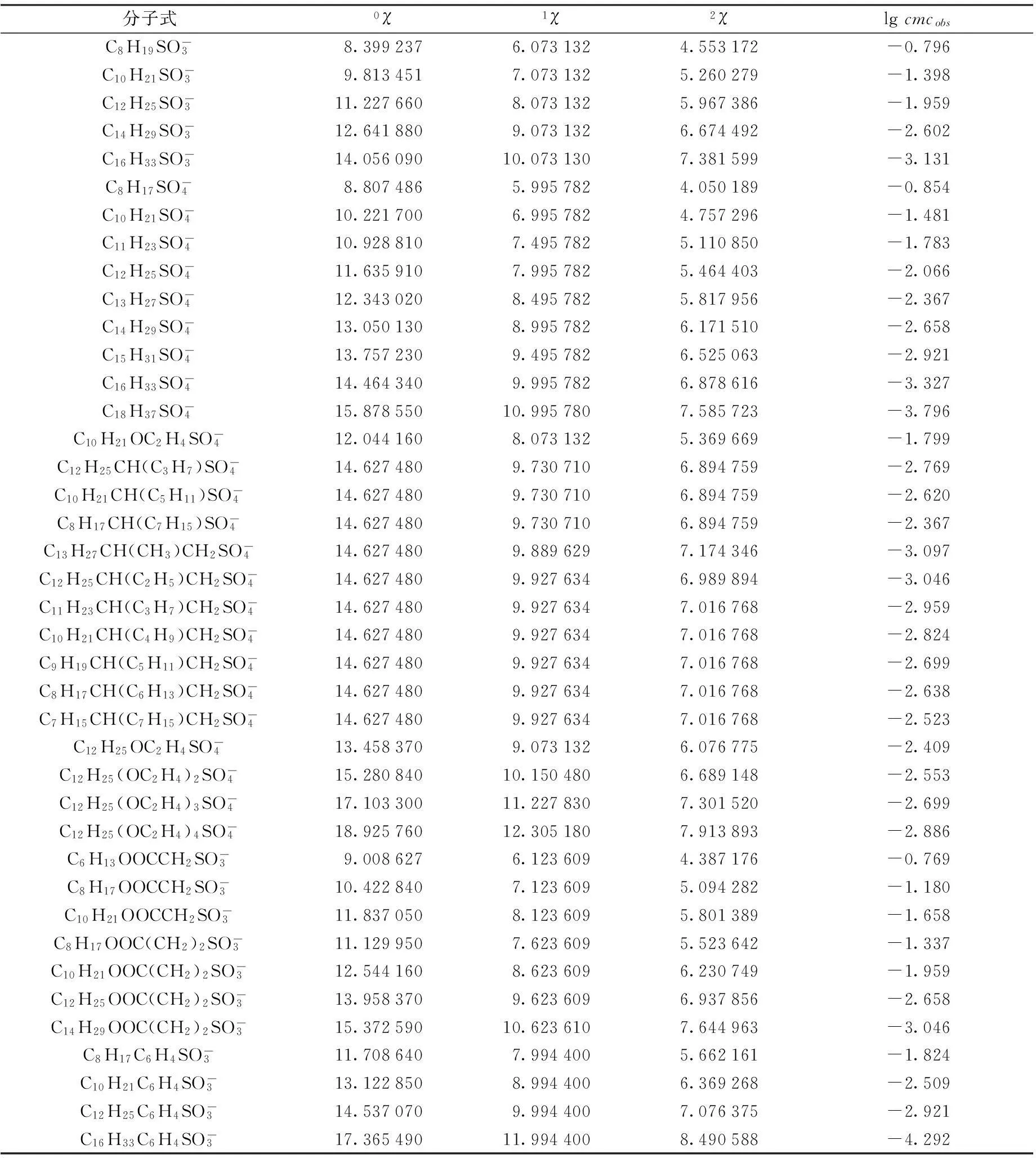
表1　阴离子表面活性剂价分子连接指数与cmc实验值

2.2多元线性回归

以0χ，1χ，2χ为自变量，lgcmcobs为因变量，利用SPSS 21.0进行多元线性回归分析，得到7个QSPR模型，统计量数据如表2所示。

经筛选得出稳定性最好的方程为：

(4)

R=0.930R2=0.864F=241.801SE=

0.295Sig=0.000

复相关系数R2=0.864代表86.4%的磺酸盐硫酸盐阴离子表面活性剂的临界胶束浓度可以由此模型表示。

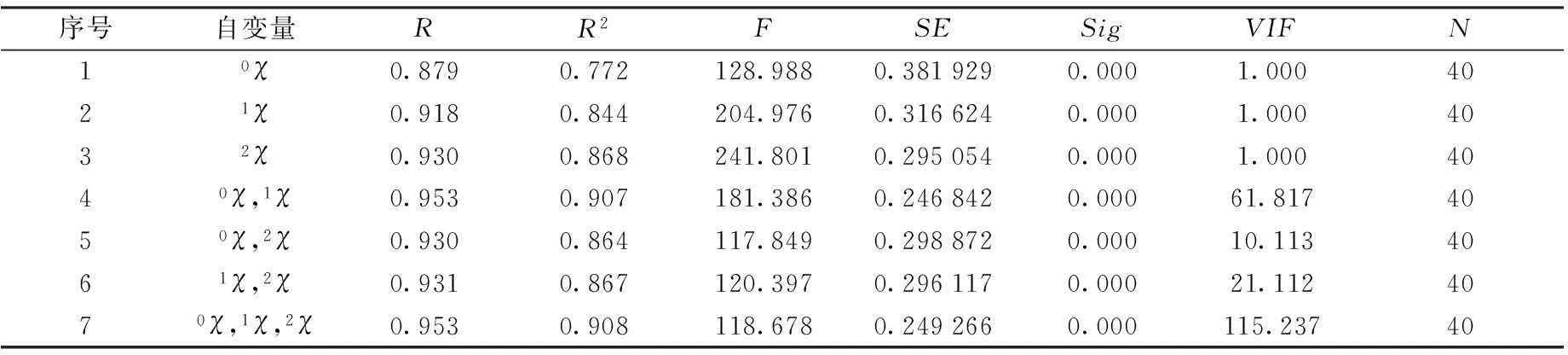
表2　QSPR模型优选

注：R为相关系数，R2为复相关系数，F为Fisher统计量，SE为标准偏差，Sig为显著性水平，VIF为变异膨胀因子。

3结果与讨论

3.1模型的内部检验

采用留一法(Leave-one-out)交叉验证进行内部检验[6]，将筛选得到的最优模型依次剔除1组数据进行建模，再将剔除的自变量2χ代入新生成的模型中求得预测值，与实验值相比较得到残差，计算得到交叉相关系数q2：

(5)

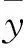
计算数据如表3所示。

表3　留一法交叉验证过程

由表3可以看出，q2>0.5说明模型具有稳健性和预测性，公式模型的q2=0.831，可以充分地认为该模型预测性良好。另外，该模型的R2-q2=0.037，该差值越小表明所建立的QSPR模型越能定量解释分子的构效关系。

3.2模型的外部验证

从样本中随机抽取了5、10、17号样本进行外部验证[6]，剔除这3组数据建模得到如下方程：

(6)

将5、10、17号样本代入进行检验，得残差值如表4所示。

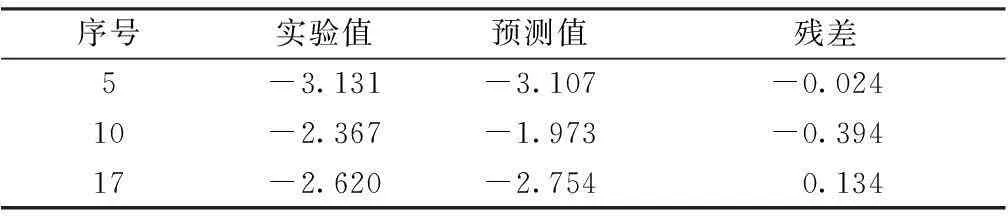
表4　随机外部验证

从样本中抽出的3组数据代入模型中，残差均较小，表明该模型基本能满足预测阴离子表面活性剂cmc的要求。

3.3模型残差分析

模型的残差越小，表明实验值和真实值越接近，证明所建立模型是成功的，用式(5)计算各组数据的残差，结果如表5所示。实验值与预测值残差频率直方图和分布图如图1所示。

表5　模型残差数据分析

由图1可以看出，实验值与预测值之间呈良好线性关系，大部分样本能比较好地分布在对角线上。此外，模型标准化残差频率分布直方图基本符合正态分布，表明建立的模型是成功的。

3.4分析方程

表面活性剂在界面定向排布，单分子层铺满整个界面后在溶液本体中才有规模地形成胶束，分子的体积(截面积)越大，铺满界面所需的分子浓度(数量)就越小。二阶价分子连接指数从一定程度上能代表分子的体积，得到的方程(4)中，2χ和函数值cmc之间呈负相关也验证了如上理论，证明该QSPR模型切合实际，有应用价值。

4结论

通过QSPR方法建立的模型方程可以预测大部分磺酸盐和硫酸盐类的阴离子表面活性剂的临界胶束浓度。方程包含了分子体积对cmc的影响程度，cmc与二阶价分子连接指数呈负相关关系，能较准确地预测cmc，而且分子连接指数计算相对简便。

参考文献

[1]纪彩虹.定量构效关系的原理方法及其研究进展[J].甘肃联合大学学报，2011，25(2):58-62.

[2]李婷婷.药物设计和研发中的定量构效关系研究进展[J].药学进展，2009，33(3):97-103．

[3]王正武，李干佐.定量结构-性质相关原理在阴离子表面活性剂临界胶束浓度预测中的应用[J].化学学报，2002，60(9):1548-1552．

[4]Zhu Z C. Quantitative structure-property relationship of the critical micelle concentration of different classes of surfactants[J].物理化学学报，2013，29(1):30-34.

[5]Rosen M J. In Surfactants and Interfacial Phenomena[M]. New York: John Wiley and Sons， Inc， 1987:33.

[6]覃礼堂，刘树深.QSAR模型内部和外部验证方法综述[J].环境化学，2013，32(7):1205-1211．

Quantitative Structure-Property Relationship of the Critical Micell Concentration of Anionic Surfactant

QI Fan, JIN Qiao, ZHANG Zhi-hong, HE Xiao-nan

(School of Chemical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, China)

Abstract:A 40-sample mathematical model derived from QSPR is built using Enter Method of SPSS 21.0 with molecular connectivityindex of rank zero to two as the independent variable and critical micell concentration as dependent variable. The best model is whose multiple correlation coefficients. It suggests that is negative correlation with the. The weak linear relationship between collining with strongly and function value is found in the screening process, so that the most important factor of is is made sure. Leave-one-out method is chosen for internal verification as a result of q2=0.831, confirming the good stability and predictability. Residuals frequency distribution histogram mainly conform to normal distribution, and with obvious linear relationship sample point in contrast diagram of experimental value and predicted value. It’s proved that this equation is able to predict the values of cationic surfactant through the statistics and statistical chart.

Key words:anionic surfactant； QSPR； critical micell concentration

收稿日期:2016-01-23

作者简介：祁凡(1995—)，男，本科生,E-mail:qifan@bipt.edu.cn；金俏(1971—)，女，博士，副教授，从事构效关系研究，通讯联系人，E-mail:jinqiao@bipt.edu.cn。

中图分类号：O6

文献标志码：A