滚动轴承故障诊断研究

王小龙

(成都大学 机械工程学院， 四川 成都　610106)



滚动轴承故障诊断研究

王小龙

(成都大学 机械工程学院， 四川 成都610106)

摘要：滚动轴承是机械工业的重要零部件，其好坏直接影响到机器最高性能的发挥，轴承在工作中承受冲击载荷与摩擦，内部结构易损坏失效，但轻微的故障极不容易发现.构建了一个故障诊断测试系统，利用MATLAB软件编程处理数据结合时域频域分析方法，最后应用BP神经网络进行模式识别故障诊断研究.

关键词：滚动轴承；MATLAB软件；BP神经网络；故障诊断

0引言

轴承广泛应用于矿山机械、农业装备、机械车辆、航空航天等领域，是国民经济的支柱产业，其发展水平的高低往往代表或制约着一个国家机械工业和其他相关产业的发展[1].滚动轴承的故障形式多样，而故障结果必然影响整个机械装置运行效率，甚至引发灾难性的后果.本研究运用现代监测方法以及信号处理分析方法，建立BP神经网络并对其进行训练，从而实现模式识别，提高滚动轴承故障诊断的正确率，具有一定的工程应用前景.

1故障诊断系统总体架构设计

滚动轴承故障状态监测诊断测试系统如图1所示.

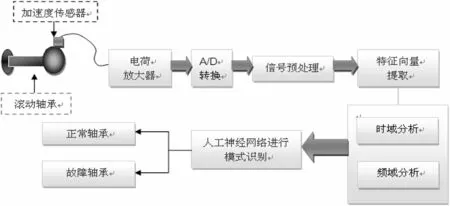
图1滚动轴承故障状态监测诊断测试系统示意图

本研究中，将加速度传感器置于轴承实验装置上，实时获取轴承的振动随机信号，电荷放大处理装置将传感器监测的振动随机信号进行放大处理，然后通过A/D转换器将轴承的模拟信号转换为计算机识别和便于处理的数字信号.转换后的数字信号通过系统信号预处理，应用MATLAB计算工具编程得到一段时间内的信号时域图，再进行傅里叶变换得到频谱图，运用反求有效特征向量的方法提取时域和频域特征值，最后，通过BP神经网络开展网络构建、误差分析.通过对以上数据进行模式识别，判断轴承是否失效，为实现滚动轴承快速化、智能化、数字化故障诊断提供一种方法，也为轴承失效模式研究和轴承长寿命设计奠定实验工程基础.

2数据导入零均值化处理

点击诊断测试系统载入故障数据中的Y2015，Workspace窗口出现轴承相关属性.载入数据成功，依次将其他数据载入，如图2所示.

图2轴承数据导入MATLAB

测试系统中，滚动轴承共有2种状态，即正常(Y)和故障(N).变频器在频率为20、25和30 Hz的工况条件下，2种状态各采集10组数据，共60组数据.选用采样频率10 kHz，采样点数为20 000，故采样时间为2 s.

信号的均值相当一个直流分量.该信号经过傅里叶变换后在ω=0处为冲激函数.若直接将其开展频谱分析，在ω=0处将出现一个较大的谱峰，并会影响在ω=0左右处的频谱曲线，使真正的故障点呈现误差，因此必须削掉均值.系统采用零均值化处理方式，消除指标量纲和数量的影响，能全面地反映原始数据中各指标的变异程度和相互影响程度.

设系统采样原始数据为Xn(n=1，2，…，N)，均值计算公式为，

(1)

零均值化处理计算公式为，

(2)

零均值化处理后，xn就变成一组均值为零的新随机信号un.以下分析以un数据为系统输入.

时域图形处理前后对比如图3所示.

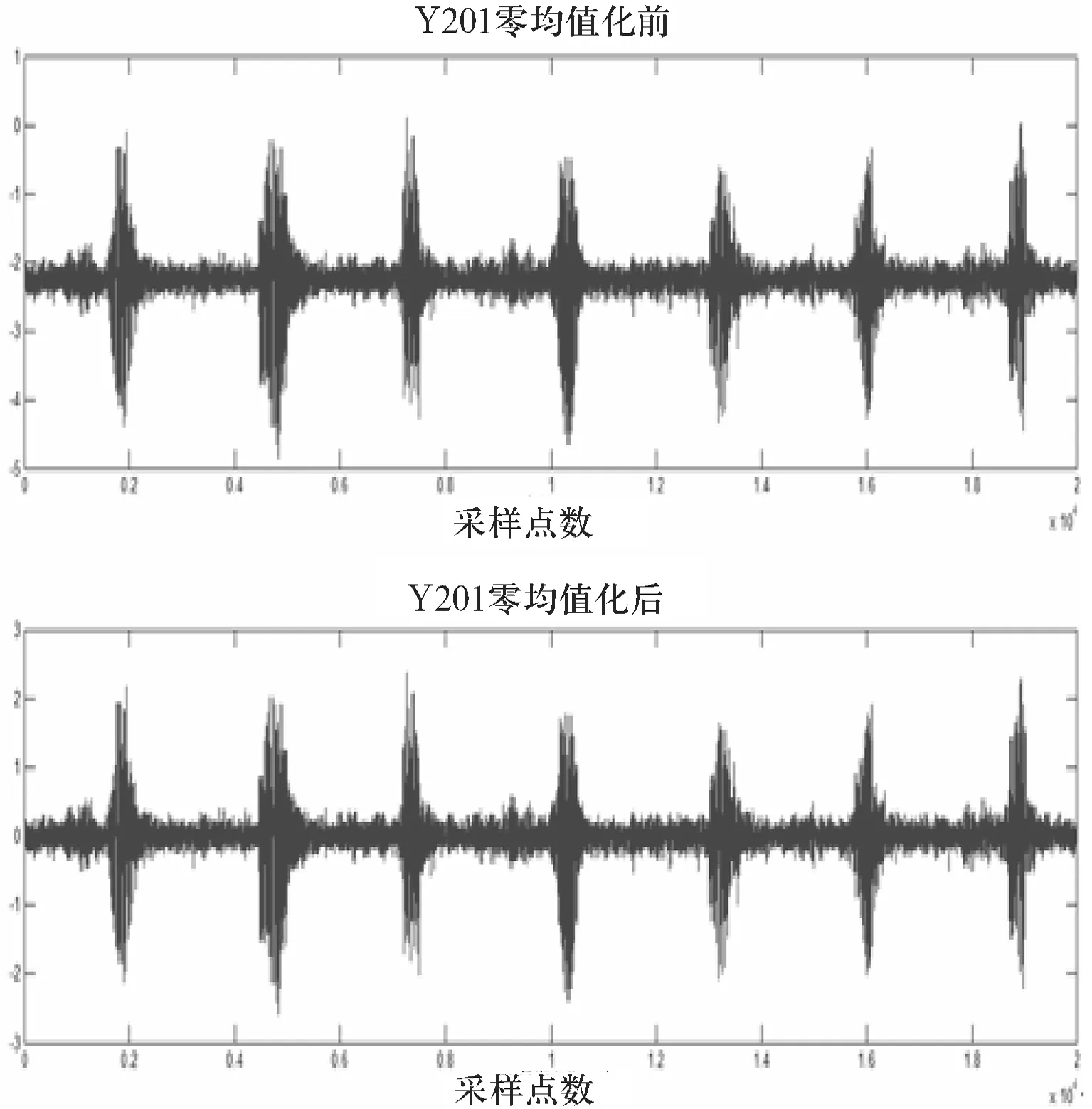
图3零均值化处理时域分析图

频域图形处理前后对比如图4所示.

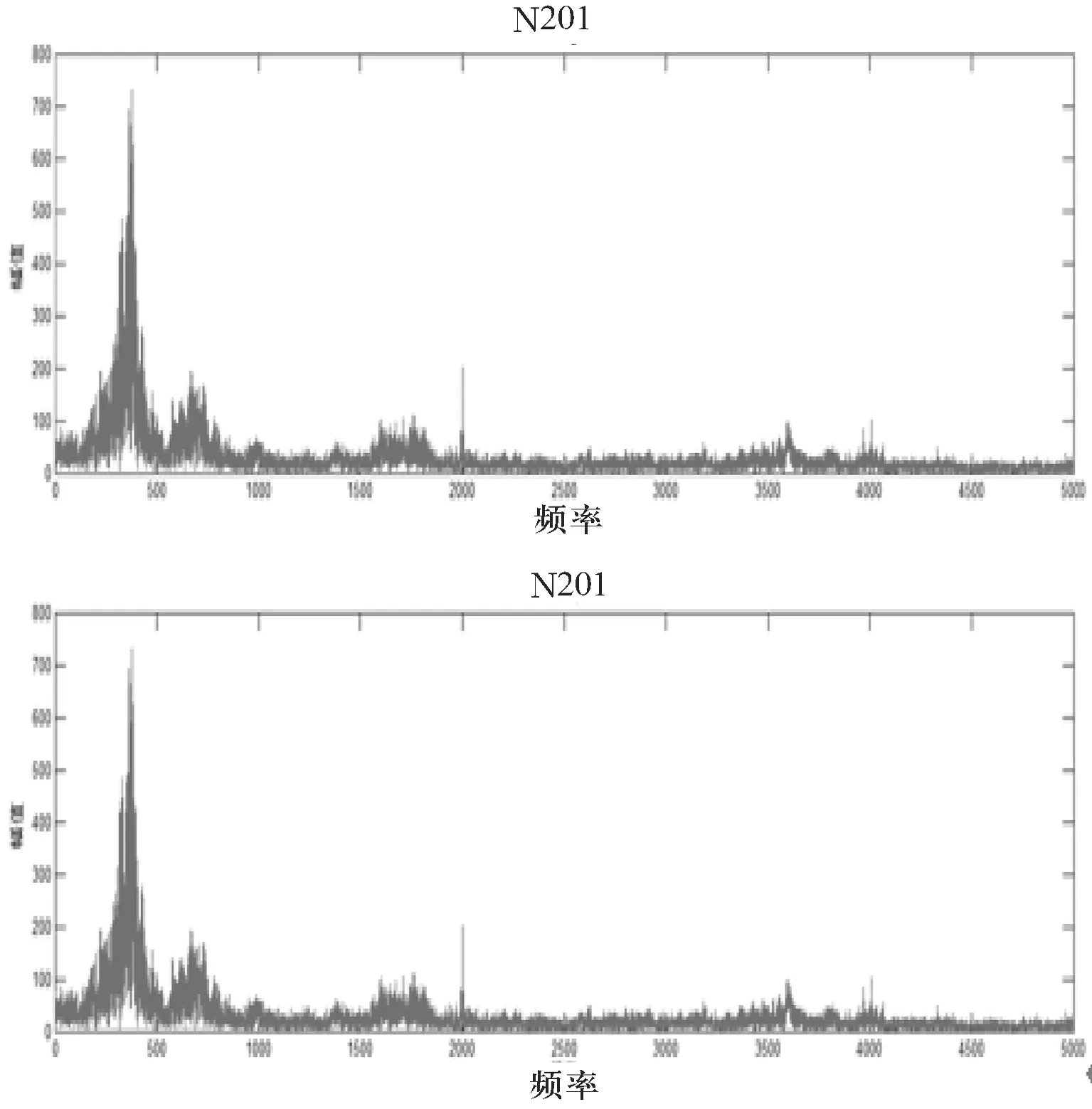
图4　零均值化处理频域分析图

从时域图形上看，波形整体向Y轴负方向平移约2个单位长度.但是从频域图可以明显看出，零均值化处理后消除了ω=0处出现的由直流分量产生的大谱峰(将近达到4.5×104)，避免了其对周围小峰值产生的负面影响，提高了数据的可靠性和真实性.

3时域分析与特征值提取

3.1时域分析方法

系统在时域分析中，设xi(i =1,2,…,N)为采集到的振动随机信号.时域分析中适用的有量纲量包括均值、方差、峰值和均方根值.适用的无量纲量有峰值因子、峭度和脉冲因子.

峰值因子(CrestFactor)，显示正常波形是否受到异常振动的冲击.它不受振动信号绝对水平影响，即使传感器的灵敏度发生变动，也不会有测量误差.

峭度(Kurtosis)，反映信号幅值分布特征的数值统计量，是归一化的4阶中心矩[2].计算公式为，

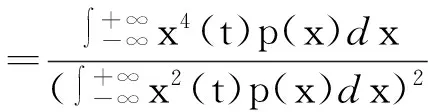
(3)

式(3)中，x(t)为去均值化后的瞬时幅值，p(x)为概率密度，σ为标准差.

通过峭度系数的计算式可以看出，分子是去均值化后的瞬时幅值的4次方，而分母为均方根值的平方，等效于分母是一个平均量.在一个随机振动时间内，必然导致分子的增长速率高于分母，若测试系统中K上升很快，表明轴承故障已显现.

脉冲因子(ImpulseFactor)，为信号峰值与信号绝对均值之比.脉冲因子对于冲击脉冲类缺陷非常敏感，特别是初期异常缺陷，脉冲因子信号有明显升高；当升高到一定程度后，随着缺陷程度的增加，信号却反向下降[3].

3.2振动信号时域特征提取

通过算例，正常轴承(Y)在运转过程中的特征信号为一个周期信号，其幅值和频率不变.仿真系统中通过先求出概论密度函数，再利用公式(3)直接计算，得出K=1.5.对于宽带高斯信号和窄带信号，通过MATLAB仿真，对不同频段的信号进行等间隔带通滤波分析，得到各频段峭度值，K窄略大于K高，约等于3.

通过算例，故障轴承(N)在运转过程中的故障特征信号为随机振动信号，没有固定的频率和周期，亦没有确定的函数表达式，也不能确定其幅值范围，但其信号服从正态分布，通过滤波处理方法，对离散信号计算各频段峭度值，得到K=42.35.故障轴承与正常轴承时域分析如图5所示.

图5故障轴承与正常轴承时域分析图

从图5可知，故障轴承的振幅大约为-5～0.5，正常轴承的振幅为-4～-0.5，即故障轴承的时域振动幅度较正常轴承大.峭度系数表征轴承接触表面出现疲劳故障时，接触面缺陷处产生的瞬时冲击幅值，疲劳故障越大，响应幅值越高，故障现象愈明显.峭度对轴承初期故障探测较敏感，轴承一旦出现故障，K值瞬时增大.

4频域分析与特征值提取

4.1频域分析方法

频域特征参数指标主要包括均方频率MSF、重心频率FC及频率方差VF.实际仿真计算时，频谱需要预先离散化处理，采样频率fs决定分析频率.利用傅立叶变换，实现滚动轴承的在线监测与诊断.上述3个参数的时域公式如下[4]，

(4)

(5)

YVF=YMSF-(YFC)2

(6)

4.2傅里叶频谱与特征提取

首先，分别比较故障轴承和正常轴承(N201、Y201)的FFT图形，如图6所示.

图6N201与Y201 FFT图

如图6所示，能够区分2个状态且能代表自身频谱的区域有：点(326，1)、区域(2560～3000)、点(3278，1)、区域(6310～6646)、区域(6850～7300).

对故障轴承数据随机抽取N202fft、N206fft、N207fft、N209fft数据对比图形如图7所示.

图7故障轴承重复性FFT谱

从图7可以看出，各个特征值的重复性较好.

对正常轴承数据随机抽取Y203fft、Y204fft、Y206fft、Y208fft数据对比图形如图8所示.

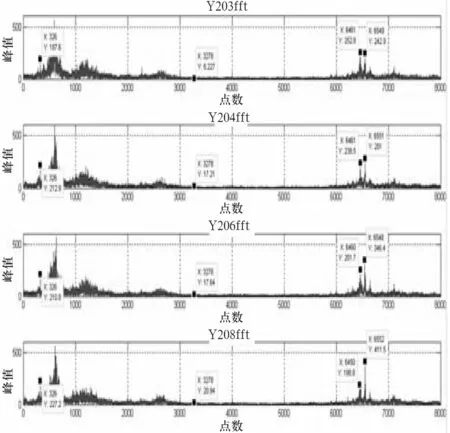
图8正常轴承重复性FFT谱

从图8可以看出，各个特征值的重复性较好.

5信号特征值归一化

为提取有效特征值，便于在不同样本之间对同一特征值进行分类比较，运用线性函数转换关系方程，将得到的所有特征值归一化到0～1区间，方程如下[4]，

Yo=(Xi-SampleMinValue)/(SampleMaxValue-

SampleMinValue)

(7)

式(7)中，Xi、Yo分别为转换前、转换后的值，SampleMaxValue、SampleMinValue分别为样本的最大值和最小值.

原始特征值归一化后数据结果如表1所示.正常轴承部分样本特征值归一化后结果如表2所示.

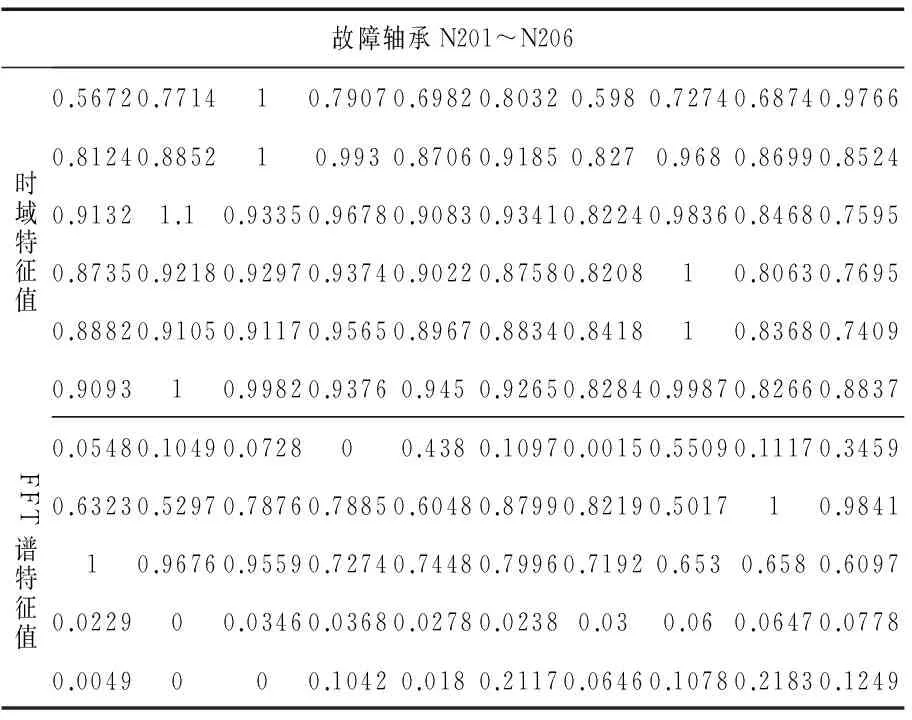
表1　故障轴承部分样本特征值归一化后结果

表2　正常轴承部分样本特征值归一化后结果

6BP神经网络模式识别

6.1输入、输出层和隐层开发

BP神经网络属于经典的前向网络，用特定的实验数据分析后提取的有效特征值作为输出矢量，将输入信号矢量联系起来，进行故障模式识别[5].依据实验样本数量，确定输入神经元个数为11，输出状态有2种，即正常轴承(Y)与故障轴承(N)，输出神经元为2.由于输入为11个神经元，输出为2个神经元，通过误差对比分析，设计一个隐层可以在一定范围内随意变化的隐层网络，隐层神经元数目在20～25之间.

6.2网络训练参数选择

设定网络的隐层神经元的传递函数为tansig[6]，输出层神经元的传递函数为logsig，结果误差为0.002，最大训练步数为1 000.结果如表3所示.

表3　隐层神经元训练误差

经过1 000次训练后，隐层神经元为21的BP网络对函数的逼近效果最好，因为它的误差最小.确定隐层的神经元数目为21.该样本BP网络的最终参数架构如表4所示.

表4　BP网络最终参数架构

6.3网络训练

训练误差为0.000 987 527，训练步数为53步.

图9网络训练误差分析

6.4网络测试

y=sim(net,测试数据)[7].

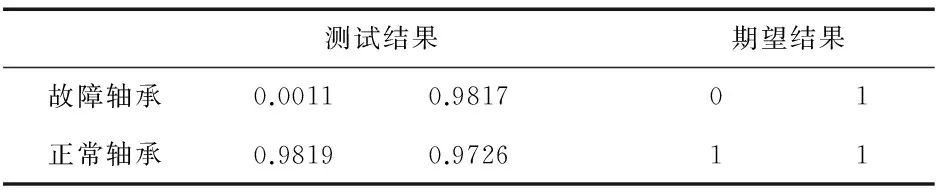
表5　网络测试结果与期望结果对比

根据表5的测试结果分析，样本数据的分类正确合理，本研究建立的BP前向神经网络模型，能够对轴承的正常状态进行识别.对于类似的故障诊断识别，可以将MATLAB测试系统测得的有效均值化数据输入到该网络，从而快速进行故障诊断识别.该网络误差小，测试结果准确可靠，具有工程应用推广价值.

7结语

本研究基于MATLAB软件进行滚动轴承故障诊断系统设计，运用数字信号分析中的零均值化、时域频域分析、特征值归一化处理思想，设计BP神经网络进行故障模式识别.通过网络训练、网络测试，确定系统误差在可控范围内.本轴承故障诊断识别系统准确率高，可以作为滚动轴承故障分析的参考依据，也为开展非接触式远程故障诊断提供了思路.

参考文献：

[1]郑德志，王黎钦，古乐，等．非平稳状态下高速滚动轴承的失效研究[J]．中国机械工程，2007，18(10)：1214-1217．

[2]张贤达．现代信号与处理[M]．北京：清华大学出版社，2002．

[3]丛玉良，王宏志．数字信号处理原理及其MATLAB实现[M]．北京：电子工业出版社，2009．

[4]杨晓明，晋玉剑，李永红．经典功率谱估计Welch法的MATLAB仿真分析[J]．电子测试，2011，18(7)：101-104．

[5]胡耀斌，厉善元，胡良斌．基于神经网络的滚动轴承故障诊断方法的研究[J]．机械设计与制造，2012，50(2)：187-189．

[6]周昌雄，陈迅，马国军．基于关联维数与BP神经网络的滚动轴承故障诊断[J]．轴承，2003，46(9)：32-34．

[7]TAN S C,LIM C P．Anensembleapplicationofconflict-resolvingART-Basedneuralnetworkstofaultdetectionanddiagnosis[J]．J Meas Sci Instr,2011，2(4)：371-377．

Research of Fault Diagnosis in Rolling Bearing

WANGXiaolong

(School of Mechanical Engineering, Chengdu University, Chengdu 610106, China)

Abstract:Rolling bearing is an important part in engineering industry which is known as the foundation of industry.Bearing quality directly affects the maximum performance of the machine.When it works,the internal structure easily becomes invalidated under the impact load and friction.However,it is not easy to find a slight fault.This paper builds a fault diagnosis system which can do fault diagnosis of pattern recognition research by using MATLAB software programming process data combined with time domain and frequency domain analysis method as well as by using the BP neural network.

Key words:rolling bearing;MATLAB software;BP neural network;troubleshooting

文章编号：1004-5422(2016)02-0178-05

收稿日期：2016-01-21.

基金项目：成都大学校青年基金(2015XJZ15)资助项目.

作者简介：王小龙(1985 — )， 男， 硕士， 汽车设计工程师， 从事汽车设计制造与车辆安全故障诊断技术研究.

中图分类号：TH133.33；TH165+.3

文献标志码：A