几乎中紧空间

罗景文， 王善荣

(1.成都理工大学 管理科学学院， 四川 成都　610059； 2.西南大学 数学与统计学院， 重庆　400715)



几乎中紧空间

罗景文1， 王善荣2

(1.成都理工大学 管理科学学院， 四川 成都610059； 2.西南大学 数学与统计学院， 重庆400715)

摘要：证明了：几乎中紧空间的闭子集是几乎中紧的；空间X是几乎中紧的当且仅当X的∀一单调开覆盖U，∃X的稠密子集D和U的一开加细U′，使得D中∀一紧集K，有(U′)K是有限集；如果Xα是|Λ|-仿紧空间，则X是几乎中紧空间⟺∀Xα是几乎中紧的；几乎中紧空间X，如果是T3空间且是可数紧空间，那么它也是紧空间.

关键词：闭子空间；几乎中紧空间；|Λ|-仿紧空间；紧有限

0引言

紧空间是一般拓扑领域内的一类非常重要的空间，通过对其性质的研究，极大地丰富了拓扑空间的内容，在拓扑学领域有着不容忽视的意义.自从1999年Grabner等[1]引入了几乎亚紧空间,并探讨了几乎亚紧空间的一些性质后，一些学者也不断对这类拓扑空间进行研究[2-7].在此基础上，本研究将meso(中)紧空间推广到几乎中紧空间，通过分析它的一些等价刻画和闭遗传性等性质，并得出一些结论.

1预备知识

本研究所述的空间均为拓扑空间，(V)K表示集族{V∈V∶V∩K≠⟩}，|A|表示集合A的势，[Λ]表示集族{F⊂Λ∶F是有限集}.

定义1[3]空间X称为是λ-仿紧的,如果X的每个势≤λ的开覆盖有一个局部有限的开加细.

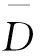
定义3[5]空间X的集族U称为紧有限的，如果X的每一紧集K仅与U中有限个元相交.

定义4[2]空间X称为几乎仿紧空间，若X的任意开覆盖U存在一开加细V和X的稠密子集D，使得V关于D是紧有限的.

定义5[4]空间X称为meso(中)紧空间，对X的任意开覆盖都存在紧有限的开加细覆盖.

定义6空间X称为几乎中紧空间，如果对X中的任意开覆盖U，存在开加细V和X的一个稠密子集D，使得V关于D是紧有限的.

2主要结论

定理1几乎中紧空间X的闭子集Y是几乎中紧的.

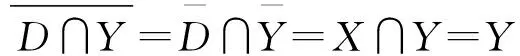
定理2空间X是几乎中紧的当且仅当X的∀一单调开覆盖U，∃X的稠密子集D和U的一开加细U′，使得D中一紧集K，有(U′)K是有限集.

证明设U是X的∀开覆盖，令U″={∪U′∶U′是U的一个有限集U∈U}，则U″是X一单调开覆盖.设V是U″的一个开加细， 且对X的稠密子集D上的∀一紧集K，有(V)K有限集.对∀V∈V，令H(V)是U的一个有限子集，有V⊆∪H(V)且W(V)={V∩U,U∈H(V)}，∵对∀V∈V，有V⊆∪W(V)，那么W=∪{W(V)∶V∈V}是U的一个开加细.令(V)K={V1,…，Vn}，则(W)K⊆W(V1)∪…∪W(Vn)且(W)K是紧有限的.∴W是U的一个开加细，且W在D上是紧有限的.得证.

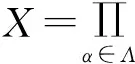
证明(⟸)∀F∈[Λ]，令，且πF∶X→YF表投射，πFE∶YE→YF表示YE到YF的映射，特别对于α∈Λ，令πα=π{α}，πα表示X到Xα的投影映射.设U是X的∀一开子集，GF(U)是YF中满足下列条件的开子集⊂U；(b)设VF是YF的∀一开子集，如果⊂U则有VF⊂GF(U).

则易知：

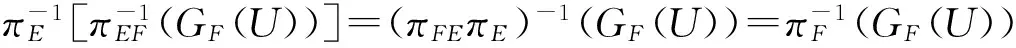
2)∀E，F∈[Λ]且F⊂E，则⊂此外，对于∀x∈U，存在F∈[Λ]和YF中的开子集VF，使得⊂U，从而VF⊂GF(U)，并且，故，

5)如果∀E，F∈[Λ]，当F⊂E时有WF⊂WE，

6)Y{WF∶F∈[Λ]}=X，从而{WF∶F∈[Λ]}是X的一个定向上升的开覆盖.故任意x∈X，∃F∈[Λ]使得x∈WF，由3)有WF=Y{}，因此存在E∈[Λ]使得).设B∈[Λ]且E⊂B，F⊂B，则⊂⊂，则，

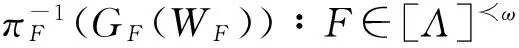
8)任意F∈[Λ]，GF(WF)⊂CF，∵AF={GF(Ua)∶a∈E}是YF的开覆盖，并且YF是几乎中紧的，则AF有一个开加细WF={WFa∶a∈E}，∃YF中的稠密子集DF，使得DF中∀紧集K，有(WF)K={WFa∈WF∶WFa∩K≠⟩}是有限集，并且任意a∈E，任意F∈[Λ]有WFa⊂GF(Ua)和⊂Y{WFa∶a∈E}，∀F∈[Λ]，∵πF是连续开映射，故是X的稠密子集，令H={}，则，

9)H是U的加细，事实上，任意a∈E，∀F∈[Λ]，WFa⊂GF(Ua)则⊂⊂Ua，

10)H是X的开覆盖，事实上任意x∈X，∵{WFa∶a∈E}是YF的开覆盖，∴∃a∈E，对任意F∈[Λ]使得xF=πF(x)∈WFa，即⊂，从而⊂，

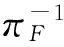
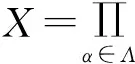
定理4几乎中紧空间X，如果是T3空间且是可数紧空间，那么它也是紧空间.

参考文献：

[1]GrabnerE,GrabnerG,VaughanJE.Nearly metacompact spaces[J].TopolAppl，1999,98(1-3):191-201.

[2]曹金文．几乎仿紧空间[J]．纯粹数学与应用数学，2003，19(1):57-60．

[3]蒋继光．一般拓扑学选讲[M]．成都:四川教育出版社，1991．

[4]高国士．拓扑空间论[M]．北京:科学出版社，2000．

[5]MancusoVJ.Mesocompactness and related properties[J].PacificJMath,1970,33(2):345-355.

[6]熊金诚.点集拓扑讲义[M].第3版.北京:高等教育出版社,2003.

[7]邓小琳．几乎弱θ加细空间[J]．南昌大学学报(理科版)，2007，31(2):128-132．

Nearly Mesocompact Spaces

LUOJingwen1,WANGShanrong2

(1.College of Management Science, Chengdu Univerisity of Technology, Chengdu 610059, China；2.School of Mathematics and Statistics，Southwest University，Chongqing 400715， China)

Abstract:This paper mainly proves the following points:(1)Every closed subspace of nearly mesocompact spaces is nearly mesocompact.(2)A space X is nearly mesocompact if and only if every monotone open cover U has an open refinement that is compact-finite on some dense subset of X.(3)Let Xαbe a |Λ|-paracompact space，then X is nearly mesocompact space if and only if Xαis nearly mesocompact for each F∈[Λ]ω．(4)nearly mesocompact spaces X,if T3-space is nearly mesocompact space,X is also mesocompact space.

Key words:closed subspace;nearly mesocompact spaces；|Λ|-paracompact space；compact-finite

文章编号：1004-5422(2016)02-0140-03

收稿日期：2016-05-16.

作者简介：罗景文(1992 — )， 男， 硕士研究生， 从事一般拓扑学研究.

中图分类号：O189.11

文献标志码：A