w-平坦模的一个注记

邢世奇， 张　勇

(成都大学 师范学院， 四川 成都　610106)



w-平坦模的一个注记

邢世奇， 张勇

(成都大学 师范学院， 四川 成都610106)

摘要：设M是R-模.如果对环R的任何极大w-理想p，Mp是自由模，并且rank(Mp)为一个固定的常数k,那么，称M有w-常秩k.w-常秩的w-有限型的w-平坦模是w-投射模.

关键词：w-投射模；w-平坦模；w-常秩

0引言

本研究约定所有的环R都是交换环，所有的模都是酉模.设M是R-模.按照文献[1]，如果对环R的任何素理想p，都有Mp是自由Rp-模，并且rank(Mp)是一个固定的常数m,那么称R-模M有常秩.众所周知，任何投射模是平坦模；反之，如果M是有常秩的平坦模，那么M是投射模[2].本研究证明具有w-常秩的w-有限型的w-平坦模是w-投射模.

下面利用文献[3]回顾w-模的一些相关背景.

设J是环R的理想.如果自然同态φ∶R→HomR(J,R)是同构，那么，称J是环R的Glaz-Vasconcelos理想，简称GV-理想.GV(R)记为环R的GV-理想的集合.

设M是R-模.令，

TorGV(M)={x∈M|存在J∈GV(R)使得

Jx=0}.

如果M=TorGV(M),那么称M是GV-挠模.如果对任何J∈GV(R)，x∈M且Jx=0总是可以推出x=0,那么称M是GV-无挠模.对任何GV-无挠模，其w-包络为，

Mw={x∈E(M)|Jx⊆M,j∈GV(R)}

1主要结果

设M是R-模，如果对环R的任何极大w-理想p,Mp是自由模，并且rank(Mp)为一个固定的常数k,那么，称M有w-常秩k.若M有常秩，则M显然有w-常秩.下面的例子表明反之未必成立.

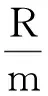
定理1设M是w-投射的R-模.如果M有w-常秩k，那么M是w-有限现型的.

证明由于M具有w-常秩k,故对R的任何极大w-理想m,Mm都是秩为k的自由Rm-模.对于给定R的任何极大w-理想m,可设，

Mm≅Rme1+…+Rmek=F

其中，{ei}是自由模F的基底.

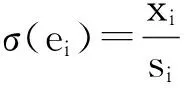
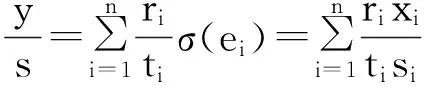
本研究拟用外幂的方法证明本研究的主要结果.

设M是R-模.记，

利用文献[1，7]中外幂的概念：设M、H是R-模，n是正整数，f∶xnM→H的交错多重线性映射.如果对任何R-模X，与任何交错多重线性映射g∶xnM→X都存在唯一的模同态h∶H→X使得下图可换，

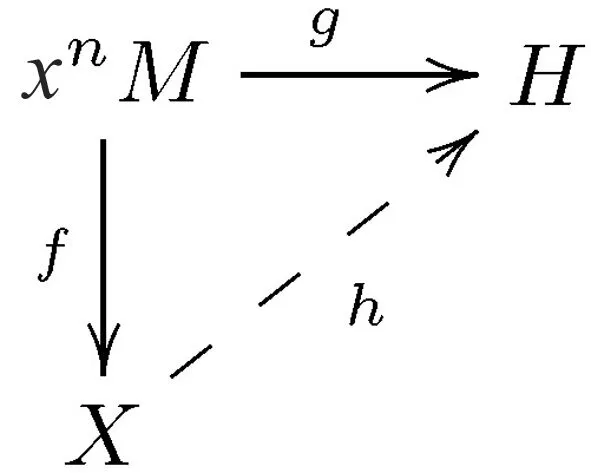
定理2设M是w-有限型的R-模.若M具有w-常秩k,则M是w-有限表现型的.

由此，可以获得w-平坦模与w-投射模的重要关系.

推论1设M是w-有限型的w-平坦的R-模.如果M具有w-常秩，那么M是w-投射模.

证明由定理2可知M是有限表现型R-模.由于M具有w-常秩，故对R的任何极大w-理想m都有Mm是自由的w-模.从而由文献[4]表明M是w-投射模.

推论2设R是整环.如果M是有限生成的平坦R-模，则M是投射模.

证明因为R是整环，故M有常秩.从而由定理2可知M是有限表现型的，当然是有限型的.因此，由文献[1，8]表明M是投射模.

参考文献：

[1]Wang F G.Commutativeringsandthetheoryofstar-operations[M].Beijing:Sicence Press,2006.

[2]Vasconcelos W V.Onfinitelygeneratedflatmodules[J].Trans Amer Math Soc,1969，138(2):505-512.

[3]Yin H Y,Wang X S,Zhu Y H,et al.w-modulesovercommutativerings[J].J Korean Math Soc,2011，48(1):146-151.

[4]Wang F G,Kim H.Twogeneralizationsofprojectivemodulesandtheirapplications[J].J Pure Appl Algebra,2015，219(6):2099-2123.

[5]Wang F G.Finitelypresentedtypemodulesandw-coherentrings[J].J Sichuan Normal Univ,2010，33(1):1-9.

[6]Kim H,Wang F G.OnLCM-stablemodules[J].J Algebra Appl,2014，13(4):1350133-1350150.

[7]Glaz S.Commutativecoherentrings[M].Berlin:Spriger-Verlag,1989.

[8]Zafrullah M.Flatnessandivertibilityofanideal[J].Comm Algebra,1990，18(7):2151-2158.

Note onw-Flat Module

XINShiqi，ZHANGYong

(Teachers School, Chengdu University, Chengdu 610106, China)

Abstract：Let M be a R-module.M is said to have w-constant k,if for any maximal w-ideal p of R,Mp is a free module of rank k.In this note,we prove that every w-flat module of w-finite type with w-constant rank is a w-projective module.

Key words:w-flat module;w-projective module;w-constant rank

文章编号：1004-5422(2016)02-0137-03

收稿日期：2016-05-15.

基金项目：成都大学人才引进计划(2081915061)资助项目.

作者简介：邢世奇(1983 — )， 男， 博士， 特聘副研究员， 从事交换代数与同调代数研究.

中图分类号：O153.3

文献标志码：A