注塑过程中注射保压阶段最小运行时间控制方法*

王立敏，朱城杰，于晶贤，高福荣

(1.辽宁石油化工大学理学院，辽宁抚顺 113001； 2.香港科技大学化学与生物分子工程系，中国香港)



注塑过程中注射保压阶段最小运行时间控制方法*

王立敏1，朱城杰1，于晶贤1，高福荣2

(1.辽宁石油化工大学理学院，辽宁抚顺 113001； 2.香港科技大学化学与生物分子工程系，中国香港)

摘要：针对注塑成型过程中的主要阶段注射段与保压段，提出了最小运行时间控制方法，在保证控制系统性能基础上使运行时间最小。考虑注射段与保压段系统模型维数不同，将注射段与保压段看做一个不同维切换系统并将其转化为等价二维系统。利用平均驻留时间方法，在二维系统理论框架内，研究系统指数稳定与最小运行时间问题。仿真结果证明所提出方法的有效性与实用价值。

关键词：注塑成型；不同维切换系统；迭代学习控制；平均驻留时间方法

联系人：王立敏，教授，主要从事间歇过程的先进控制、故障诊断与容错控制研究

注塑过程在每个批次内，一般需要经历合模、注射、保压、冷却及开模等五个阶段。其中注塑、保压两个相邻阶段对最终产品品质影响最大，且需要实现的控制策略及目标均不相同。在注射阶段，所需要控制的关键变量是注射速度；在保压阶段，其目标是控制保压压力。因而，称这两个阶段的切换为速度/压力切换。由于需要实现不同的控制策略及目标，这两个阶段将相互影响且两阶段模型维数不同。以往研究成果，仅考虑单一阶段的高精度控制[1–7]。单阶段的最优控制并不能保证全局最优和生产的整体高效运行。此外，在实际工业过程中，各阶段的运行时间多由实际经验或估计得到，这也在一定程度上延长了注塑过程实际运行所需要的时间，给注塑成型的高效运行带来了本质困难。为得到注射保压段最小运行时间寻求新的控制方法极其迫切。

在2008 年，Wang Youqing等[8]针对注塑过程相邻阶段就其切换条件与切换时间的控制问题做了初步研究，但此文研究的注塑过程阶段运行时间，只求得了注射阶段时间。为了解决上述问题，笔者提出了与系统状态相关的切换条件结合平均驻留时间方法，利用注塑过程本身具有的特性如重复性、二维特性等本质特性，设计混杂迭代学习控制律，确保系统运行时间最小，同时保证系统最优控制性能。

1　等价模型再描述

如文献[8]中描述，在注塑过程中，注射与保压两个阶段表示成切换系统模型，利用迭代学习控制方法，得到等价二维误差系统模型如下：

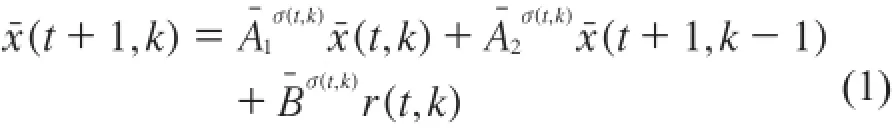
处阶段，表示的含义均如文献[8]所示。迭代学习更新律设计为：

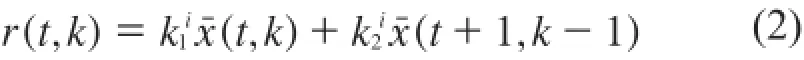
其中i∈{1，2}。

笔者主要考虑的问题是设计迭代学习更新律，使得上述两个阶段系统运行时间最小。笔者要考虑的问题均基于此模型。下面给出2D 条件下两个新的定义。

2　主要结果

2.1混杂迭代学习控制器设计

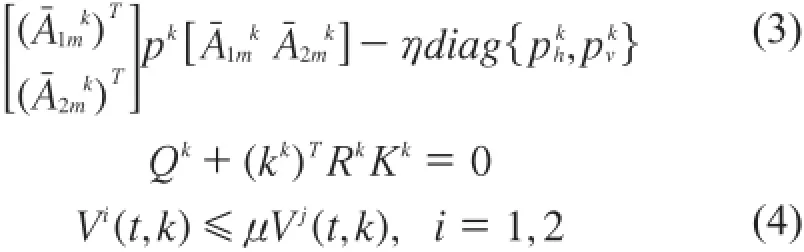
则对于满足式(1)的切换信号下，闭环系统稳定。

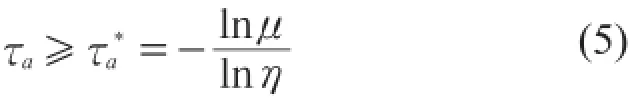
证明.假设第kth子系统被激活，对于kth子系统，选择如下的Lyapunov泛函：

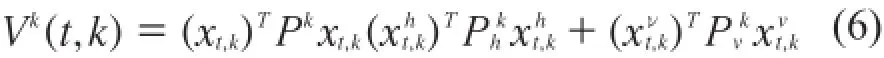
为待求的正定矩阵。

定义：

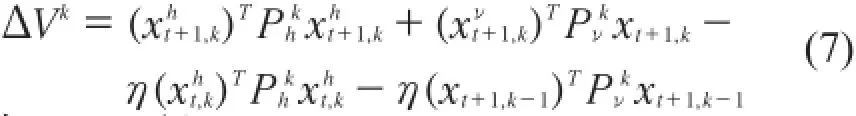
代入(3)，得：

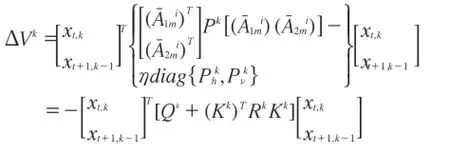
对于任意的非负整数D及D>max(z1，z2)，利用上式可得：

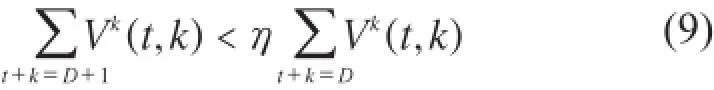
假设初始批次及结束批次分别为kk-υ+1，kk，定义对于D∈，有：

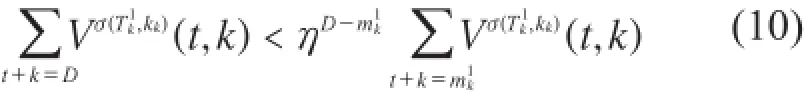
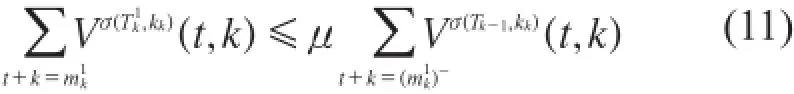
从定义2可知：

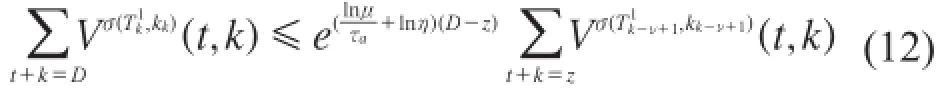
定义，下式成立：

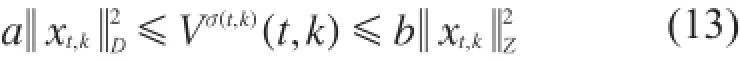
因此

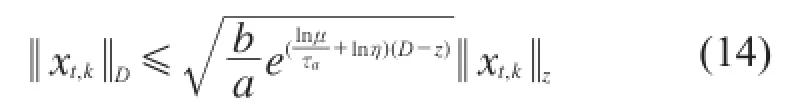
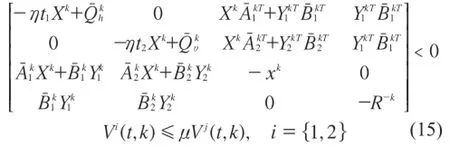
则对于满足式(15)的切换信号下，闭环系统经由控制器律(17)镇定。

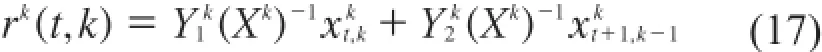
定理2的获得需将定理1转化不等式，然后利用矩阵转换便可得到，在此省略。

2.2最小运行时间计算

求解定理2，得到控制律增益为：

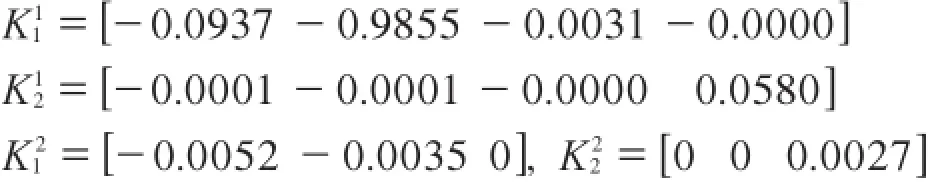
3　控制效果分析

由于运行环境复杂多变，在实际注塑过程中，扰动是不可避免的，在本部分将考虑重复扰动与非重复扰动两种情况，对笔者所提出方法的控制效果进行验证。为评价控制效果，引入如下评价指标：

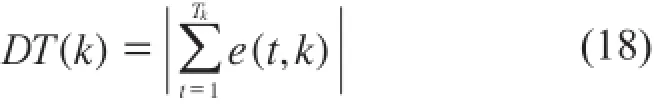
3.1重复扰动

在注射段扰动设为w=cos(t)×[0.1 0.2 0.3]T，在保压段，扰动设计为w=cos(t)×[0.1 0.2]T。图1～图3显示了控制效果。图1为所有批次评价指标与切换时间。图2为部分批次的输出曲线，图3为所有批次的输出结果。经过几个批次的不稳定运行，系统可以跟踪到设定值。

图1　各批次评价指标与切换时间

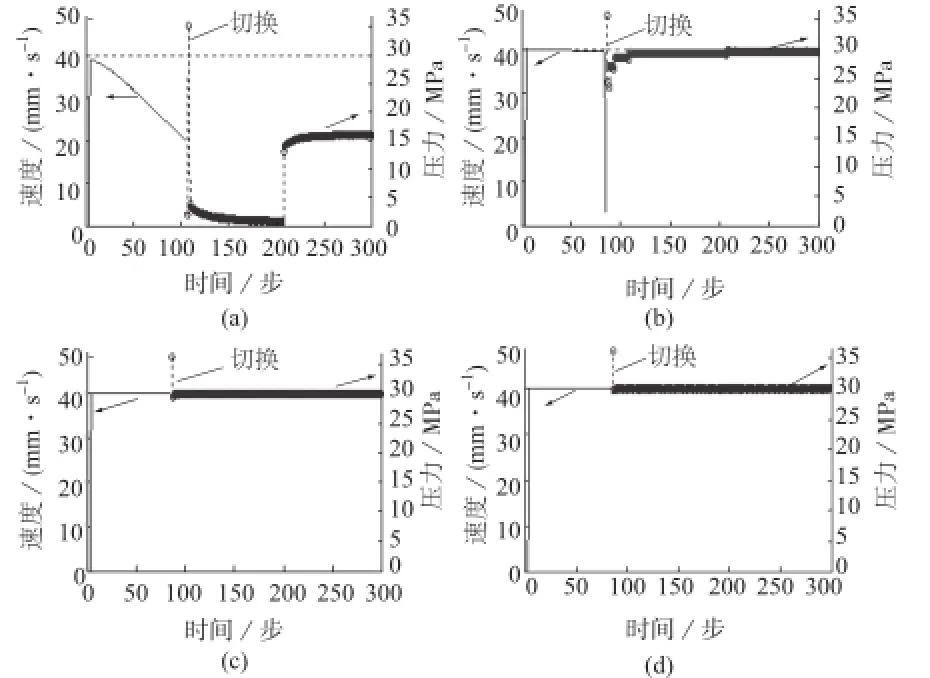
图2　部分批次输出曲线

图3　所有批次输出曲线

从图1可以看出，控制效果可很快收敛到设定值，且运行时间较根据经验得到的时间[6]大幅减小，验证了所提出方法的实用价值。

3.2非重复扰动

在这一部分，研究非重复扰动下系统控制性能。在注射段，扰动设计为w(t，k)=0.5×[Δ1Δ2Δ3]T；在保压段，扰动设计为w(t，k)=0.5×[Δ1Δ2]T，其中Δi(i=1，2，3)均为[0，1]内的随机数。图4为所有批次残差与切换时间，由于非重复扰动的影响，残差有所提高，这是可以接受的。而从控制效果看，系统可以达到满意的控制效果。由于扰动为非重复，因而切换时间会有小幅变化，这是可以理解的。图5为部分批次的输出曲线，图6为所有批次的输出结果。

图4　各批次评价指标与切换时间

图5　部分批次输出曲线

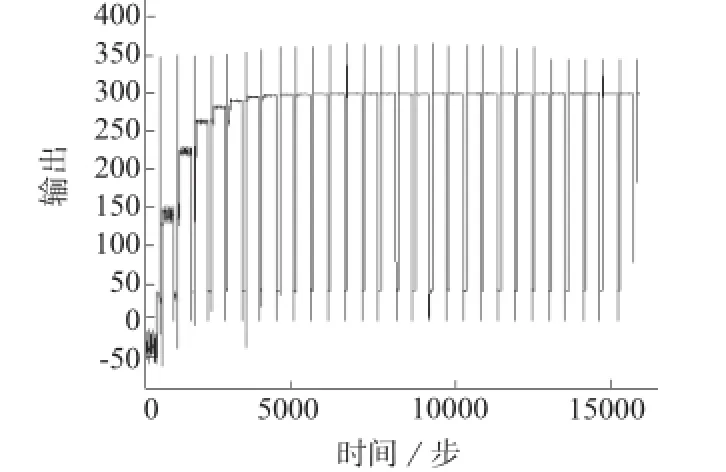
图6　所有批次输出曲线

4　结论

阶段运行直接影响批次时间，进而影响注塑成型工业的生产效率，笔者利用平均驻留时间方法，研究注射段与保压段这两个不同维系统的最小运行时间控制问题。在保证控制效果的前提下，相比于通过经验或给定方法，大幅减小了运行时间。为实际注塑成型过程提供了一种行之有效的方法，具有很好的使用价值。

参 考 文 献

[1] Mo Shengyong，Wang Limin，Yao Yuan，et al. Two-time dimensional dynamic matrix control for batch processes with convergence analysis against the 2D interval uncertainty[J]. Journal of Process Control，2012，22:899–914.

[2] Wang Limin，Mo Shengyong，Zhou Donghua，et al. Delay-rangedependent guaranteed cost control for batch processes with state delay[J]. AIChE Journal，2013，59(6):2 033–2 045.

[3] Wang Limin，Mo Shengyong，Zhou Donghua，et al. H∞ design of 2D controller for batch processes with uncertainties and interval time-varying delays[J]. Control Engineering Practice，2013，21:1 321–1 333.

[4] Wang Limin，Mo Shengyong，Zhou Donghua，et al.Delay-rangedependent robust 2D iterative learning control for batch processes with state delay and uncertainties[J]. Journal of Process Control，2013，23:715–730.

[5] Liu Tao，Gao Furong.Robust two-dimensional iterative learning control for batch processes with state delay and timevarying uncertainties[J].Chemical Engineering Science，2010，65:6 134–6 144.

[6] Wang Limin，Mo Shengyong，Zhou Donghua，et al. Robust delay dependent iterative learning fault-tolerant control for batch processes with state delay and actuator failures[J]. Journal of Process Control，2012，22:1 273–1 286.

[7] Wang Limin，Mo Shengyong，Zhou Donghua，et al. Delay-rangedependent method for iterative learning fault-tolerant guaranteed cost control for batch processes[J]. Industrial & Engineering Chemistry Research，2013，52: 2 661–2 671.

[8] Wang Youqing，Zhou Donghua，Gao Furong. Iterative learning model predictive control for multi-phase batch processes[J]. Journal of Process Control，2008，18:543–557.

Minimum Running Time Control Method for Filling and Packing Stages of Injecting Modeling

Wang Limin1， Zhu Chengjie1， Yu Jingxian1， Gao Furong2
(1. College of Sciences， Liaoning Shihua University， Fushun 113001， China； 2. Department of Chemical and Biomolecular Engineering，Hong Kong University of Science and Technology， Hong Kong， China)

Abstract：Aimed at the filling and packing-holding phase of injecting modeling，a novel minimum running time method was proposed，meanwhile，the control performance was guaranteed. The filling and packing-holding phase were treated as a different dimensional switched system considering that the model of the two phases are different dimensional and were transformed into an equivalent two-dimensional (2D)system. Under 2D system framework，the exponential stability and minimum running time problems were studied by using an average dwell time method. Simulation demonstrated the effectiveness and merits of the proposed method.

Keywords：injection molding；different dimensional switched system；iterative learning control；average dwell time method

中图分类号：TQ320.66

文献标识码：A

文章编号：1001-3539(2016)04-0053-04

doi:10.3969/j.issn.1001-3539.2016.04.012

收稿日期：2016-02-03

*国家自然科学基金项目(61227005)，中国博士后面上基金项目(2014M560972)，辽宁省高等学校优秀人才支持计划(LJQ2014039)，广东省科技计划项目(2013B011301012)