一种采用双目视觉加惯性测量的航天器组合相对导航方法*
赵逸伦 乔 兵 靳永强 郁 丰
1.南京航空航天大学,南京210000 2.上海宇航系统工程研究所,上海201100
一种采用双目视觉加惯性测量的航天器组合相对导航方法*
赵逸伦1乔 兵1靳永强2郁 丰1
1.南京航空航天大学,南京210000 2.上海宇航系统工程研究所,上海201100

以对偶四元数为数学工具,在机器视觉和惯性导航的基础上提出了一种新的航天器相对导航算法。介绍了对偶四元数的空间位姿模型,并基于共线投影原理建立了双目视觉的测量模型,为系统提供观测数据。根据航天器运动学模型推导其状态方程,并在此基础上设计了扩展卡尔曼滤波器。通过计算机仿真验证了该相对导航算法的有效性。仿真结果表明该方法对航天器的相对位置、姿态和速度均具有良好的估计精度,可以满足交会对接、航天器捕获等任务的精度需求。 关键词 双目视觉;组合相对导航;对偶四元数;卡尔曼滤波;航天器
两航天器间的相对位姿问题本质上可以归结为两不共点坐标系之间的螺旋变换问题[1]。目前用于描述两坐标系位姿的方法有很多,常见的有欧拉角,方向余弦矩阵以及哈密顿四元数。方向余弦矩阵的几何意义明确,但因其多达6个约束条件而影响其广泛使用[1]。欧拉角的物理意义比较直观,但运动学方程复杂不便于计算。四元数的引入,虽然弥补了旋转矩阵在计算时的溢出缺陷,但是仍将坐标系的旋转与平移(或者说是坐标系间的相对位置与姿态)分开处理。这种办法一方面会影响相对位置和姿态求解的精度,另一方面在位姿测控中,增加了系统的复杂性。
Chales定理表明[2]:任何刚体空间运动都可通过先绕某根轴旋转再沿同一根轴平移的螺旋运动来实现。基于Chales定理把旋转和平移统一考虑,产生了对偶四元数的概念。对偶四元数继承了四元数的很多性质和优点,能避免在大角度旋转时运算中的奇异性和姿态矩阵的正交性问题[3]。在计算机视觉[4]、机器人[5]及捷联惯性导航[6]等领域应用中显示出了其数学表达式直观、明了和计算效率高等优势。可见,对偶四元数是一种适用于航天器相对导航任务模型建立的数学工具。
在航天器交会对接、空间目标跟踪和在轨服务等多项空间任务中,通常采用光学敏感器作为观测手段,来测量目标航天器与追踪航天器间的相对位置及姿态[7]。一般的做法是在目标航天器上设置若干个光学特征点,由安装在追踪航天器上的CCD相机识别,并匹配这些光学特征点,根据成像信息解算相对位置及姿态。
但是对于传统的单目视觉测量方法,其测量方程为非线性方程,需要迭代求解[8],不仅需要较为精确的初始值,而且很可能会产生多值结果,对求解的速度精度都造成很大影响。此外,单一的光学导航方法亦存在一些缺点和不足:1)由于测量过程中需要对光学特征点进行检测和匹配,导致测量结果输出不够密集,更新速度较慢;2)光学敏感器只能输出单一的位置和姿态信息,对速度、角速度只能在位置和姿态测量结果的基础上做差分得到粗略估计;3)在近距离相对导航中光学测量单元可能会由于特征点遮挡出现输出中断的情况。与光学导航相比,惯性导航存在以下优势[4]: 1)不依赖于任何外界信息,可全天候工作; 2)能连续输出载体的加速度、角速度,输出的导航信息有很好的连续性; 3)数据更新率高,短期精度和稳定性较好。不过惯性元件由于存在初始误差、漂移和噪声等原因,长时间导航会产生较大累积误差。鉴于单目视觉测量和惯性导航存在的固有缺陷,本文提出一种双目摄像机加惯性原件的组合相对导航方法,可有效测量目标星和追踪星间的相对姿态,高精度的估计出追踪星的各类运动学参数,为多航天器协同任务的完成提供保障。
1 对偶四元数空间变换模型
1.1 对偶四元数
对偶数的概念由英国数学家Clifford于1873年首次提出[9],对偶四元数是实部和对偶部均为四元数的对偶数。限于篇幅,详情见文献[9]。
如果把空间三维向量看作实部为0的四元数,则对偶四元数可用于表示空间直线:设空间直线L的方向向量为l,关于参考坐标系原点的矩为m,则L可表示为
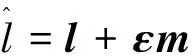
(1)
1.2 基于对偶四元数的空间位姿变换
限于篇幅,下面不加证明的给出基于四元数和对偶四元数的位姿变换模型。
若坐标系A绕n轴旋转θ角后与坐标系B重合,定义从A系至B系的转换四元数:
(2)
设向量a在A系和B系下的坐标分别为aA和aB,有:
aB=q*·aA·q
(3)
若坐标系A绕n轴旋转θ角,再平移t后与坐标系B重合,定义从A系至B系的转换对偶四元数:
(4)
其中,q的定义同式(2),tA,tB分别表示平移向量t在A系和B系下的坐标。
(5)
对比式(3)和(5),可以看到四元数坐标变换与对偶四元数坐标变换有完全相同的形式。事实上,四元数的大部分性质都被对偶四元数完全继承了。
2 双目视觉和惯性元件测量模型
2.1 视觉测量的坐标系定义
为便于分析建立如图1所示的像平面坐标系、相机坐标系和目标航天器坐标系,并分别定义如下:
1)像平面坐标系:原点O1位于像平面中心,即摄像机光轴与成像平面的交点,x轴和y轴分别与图像平面的两邻边平行,记为O1系;
2)摄像机坐标系:原点为摄像机光心Oc,Xc轴和Yc轴分别与图像坐标系的x轴和y轴平行,Zc轴为摄像机的光轴,与图像平面垂直,记为Oc系;
3)目标航天器本体坐标系:原点Oa位于目标航天器质心,x,y,z轴与航天器的3个惯量主轴重合,记为Oa系。
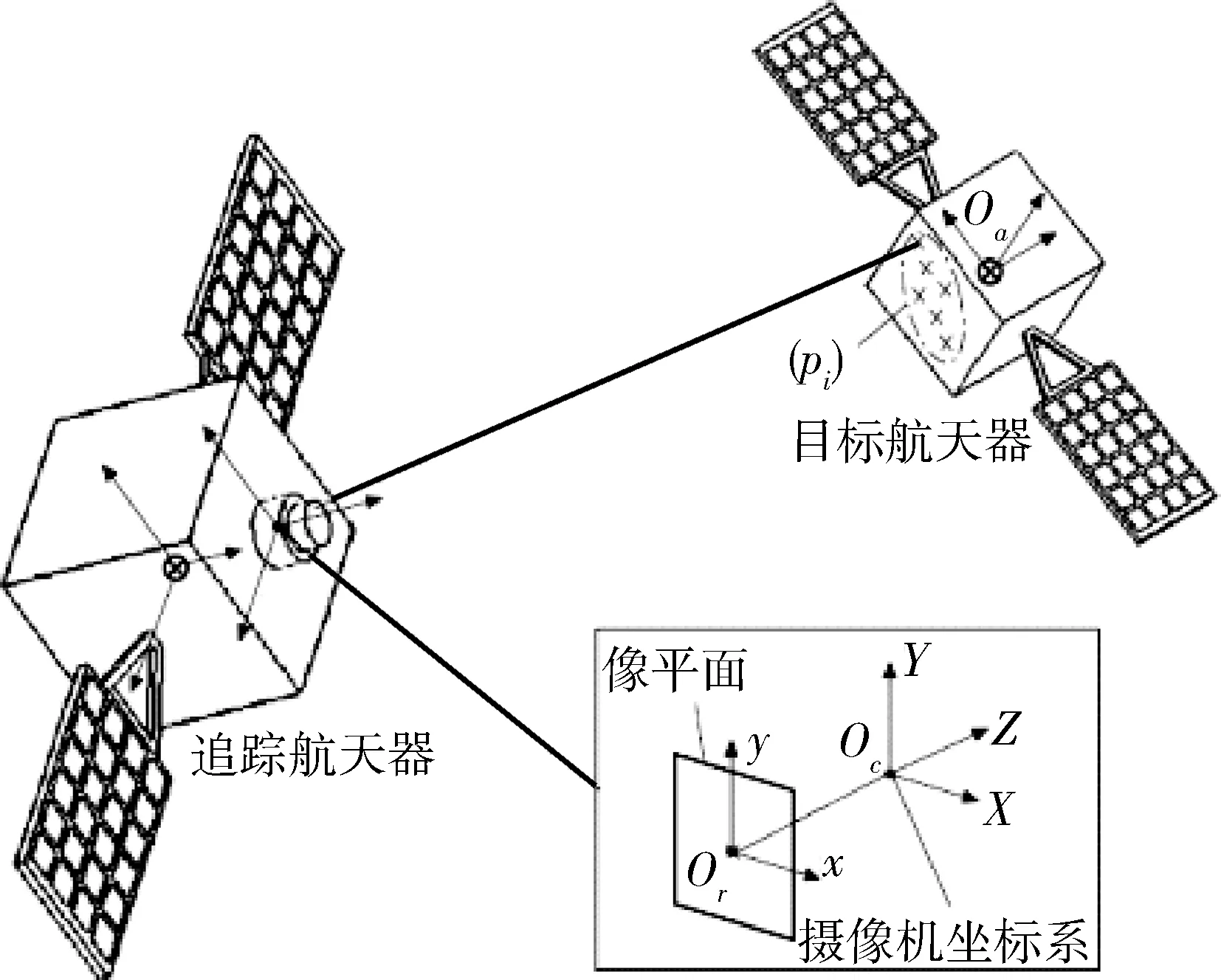
图1 坐标系定义示意图
2.2 双目视觉测量模型
所谓双目视觉,指的是同时用2台摄像机对同一目标拍摄2幅图像以确定物体空间方位的方法[10]。图2描绘了平行双目视觉成像系统的基本原理。
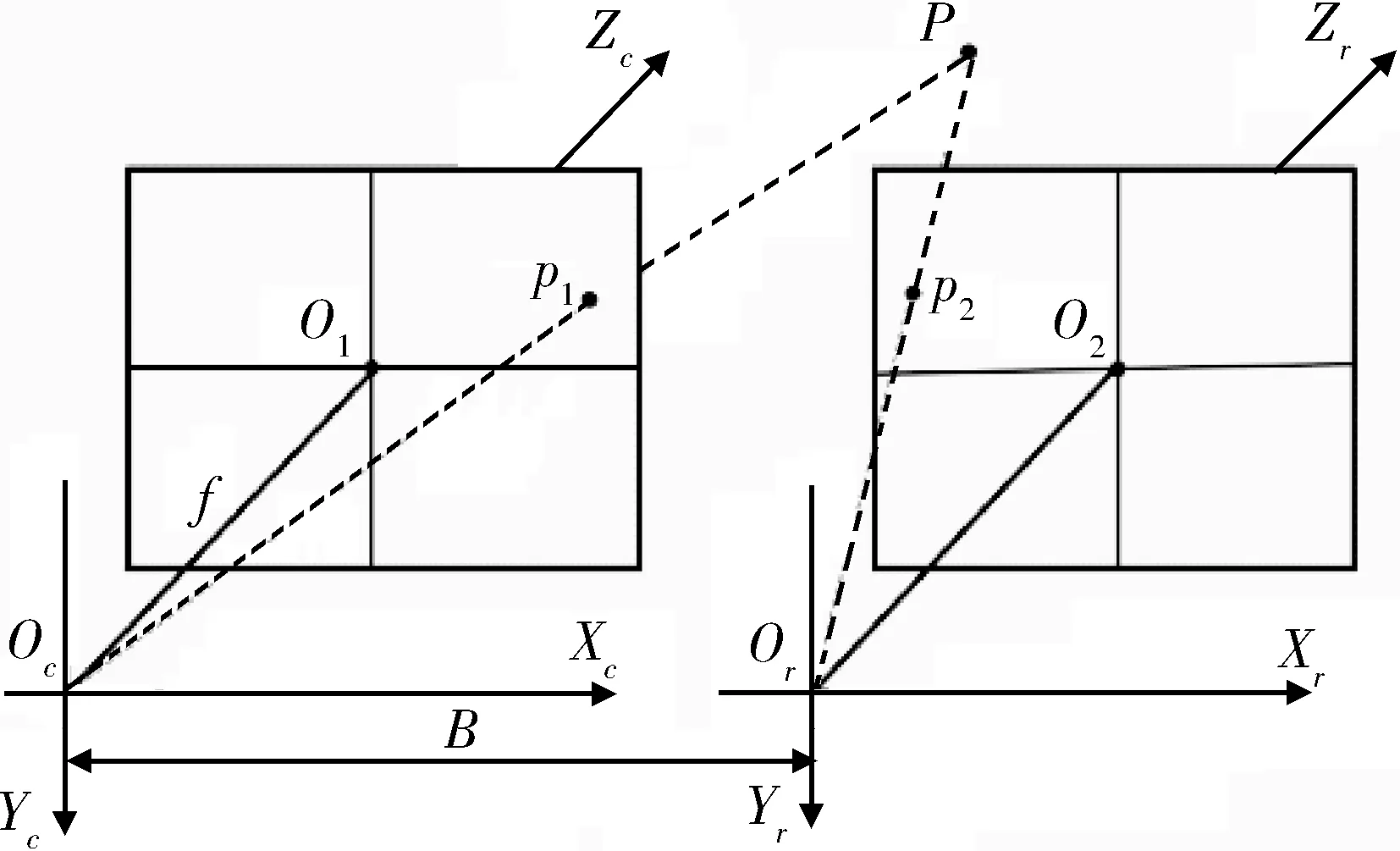
图2 平行双目视觉成像原理
左右摄像机的光心分别为Oc和Or,两光轴平行且分别交成像平面于O1和O2点。两摄像机的Z轴分别与各自的光轴重合,X轴则位于同一条直线上。左右摄像机光心的连线OcOr称为基线,定义线段OcOr的长度为基线距B。设P点在左右摄像机成像平面上投影的坐标分别为p1(x1,y1),p2(x2,y2),P点在左右摄像机坐标下的位置分别是(Xc,Yc,Zc),(Xr,Yr,Zr),由平行双目视觉系统的结构易知:Xc=Xr+B,Yc=Yr,Zc=Zr,y1=y2。再由投影原理可得如下关系式:
(6)
由此可算出P点在左摄像机下的坐标:
(7)
2.3 相对位姿参数的解算

(8)
将式(8)展开,可得:
(9)
即:
(10)
对式(10)等号两边同时左乘q并整理得到:
(11)
根据四元数乘法法则,将式(11)中第1式写为矩阵乘法的形式:
(12)

(13)
将式(13)带入式(11)中第2式,并写成矩阵乘法的形式,得:
(14)
解该非齐次线性方程组即得平移向量t。
2.4 惯性元件的测量模型
惯性测量元件中的加速度计和陀螺可分别测量航天器相对于惯性空间的加速度和角速度。对于捷联式惯性系统,输出的是载体相对于惯性系的非引力加速度和角速度在载体坐标系上的投影。在忽略安装误差和标定误差的情况下,加速度计的测量输出包括非引力加速度的真实值、加速度计漂移和量测噪声3个部分[11],即:
am=a+ba+ηa

(16)

与加速度计类似,陀螺的输出包括真实角速度、陀螺漂移和测量白噪声3个部分,即
ωm=ω+bω+ηω
(17)
式中,ηω和bω的定义同ηa和ba类似,不再赘述。
3 系统动态模型建立
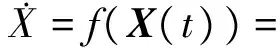
(18)
其中,A(q)代表与q对应的方向余弦矩阵,ωa为目标航天器相对惯性系的角速度在Oa系下的坐标,M,N是基于C-W方程得到的修正项,分别定义为:

G(t),w(t)分别为噪声驱动矩阵和噪声项。状态转移矩阵:
Φk/k-1=eFk/k-1·Δt
(19)
其中:
(20)
导航测量方程:
(21)
根据文献[1],双目摄像机对位置的估计精度与距离为负相关的关系,即距离越近对距离的测量精度越高;而对姿态的测量精度与距离无关。根据双目摄像机的测量特点,可对测量噪声的方差做合理近似。
4 仿真验证和分析
以两航天器交会对接的逼近段为任务背景进行仿真验证,下面以表格形式给出仿真所需的各类参数。

表1 仿真参数

图3 相对位置估计误差


图4 四元数估计误差

图5 四元数测量误差


图6 速度估计误差
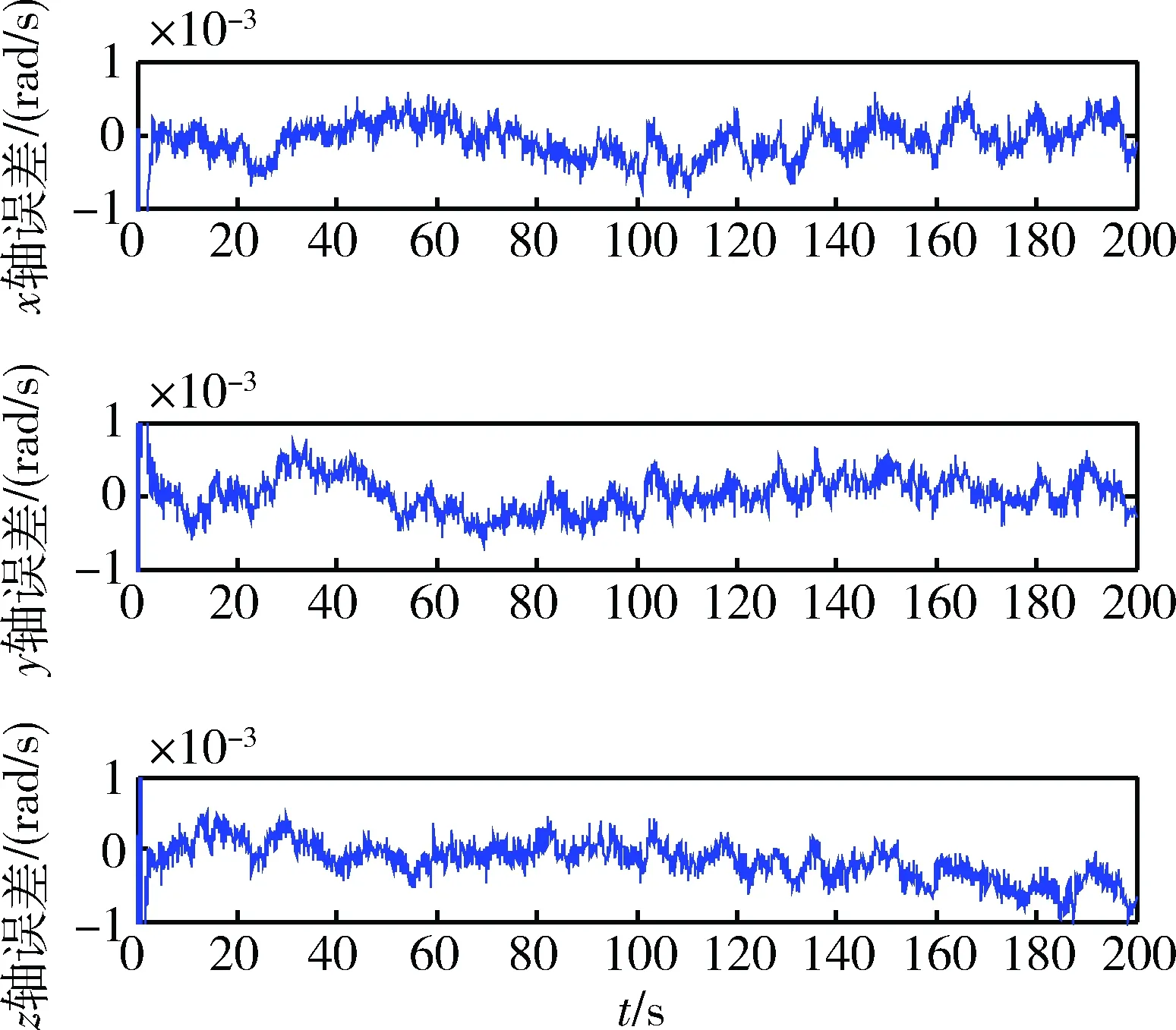
图7 角速度估计误差
5 总结与展望
提出了一种双目视觉加惯性元件的航天器组合相对导航方法,并在此基础上设计了卡尔曼滤波器。首先介绍了基于对偶四元数的空间变换方法,然后以此为数学工具给出了双目视觉条件下测量航天相对位姿的方法。最后以航天器交会对接逼近段为任务背景建立了系统的动态模型并进行了计算机仿真。仿真结果表明,该方法很好地发挥了视觉导航和惯性导航各自的优点而相互弥补了各自的不足,能够实时准确地估计航天器相对运动中的各类参数。该方法可为航天器捕获、航天器在轨维修等近地空间任务提供技术支持。
[1] 钱萍,王惠南. 基于对偶四元数的航天器交会对接位姿双目视觉测量算法 [J].宇航学报,2013,34(1):32-38.(QianPing,WangHuinan.ABinocularVisionAlgorithmBasedonDualQuaternionforRelativePositionandAttitudeDeterminationofRVDSpacecrafts[J].JournalofAstronautics,2013,34(1):32-38.)
[2] 武元新.对偶四元数导航算法与非线性高斯滤波研究[D].长沙:国防科学技术大学,2005.(WuYuanxin.ResearehonDualQuaternionNavigationAlgorithmandNonlinearGaussianFiltering[D].Changsha:NationalUniversityofDeefnseTechnolog,2005.)
[3] 崔本杰.基于对偶四元数的航天器相对导航方法研究[D].哈尔滨:哈尔滨工业大学,2009.(CuiBenjie.StudyOnRelativeNavigationMethodForSpacecraftBasedOnDualQuaternion[D].Harbin:HarbinInstituteofTechnology. 2009.)
[4]LadislavK,StevenC,CarolO.DualQuaternionsforRigidTransformationBlending[R].Ireland:DublinUniversity, 2006.
[5]DaniilidisK.Hand-eyeCalibrationUsingDualQuaternions[J].InternationalJournalofRoboticsResearch, 1999(18): 286-298.
[6]WuYuanxin,HuXiaoping,HuDewen.StrapdownInertialNavigationSystemAlgorithmsBasedonDualQuaternions[J].IEEETransactionsonAerospaceandElectronicSystems, 2005, 41(1): 110-132.
[7] 贺江涛.航天器近距离交会自主光学相对导航算法研究[D].南京:南京航空航天大学,2012.(HeJiangtao.AutonomousOpticalRelativeNavigationAlgorithmsforSpacecraftClose-rangeRendezvous[D].Nanjing:NanjingUniversityofAeronauticsandAstronautics,2012.)
[8]CaoXibin,ZhangShijie.AnIterativeMethodforVision-basedRelativePoseParametersofRVDSpacecraft[J].JournalofHarbinInstituteofTechnology,2005,37(8):691-694.
[9]JoanL,AnthonyN,ChrisJL,etal.AUnifiedMathematicalLanguageforPhysicsandEngineeringinthe21stCentury[J].PhilTrans:Mathematical,PhysicalandEngineeringSciences,2000,358(1765): 21-39.
[10] 李江游.双目视觉位姿估计算法研究[D].哈尔滨:黑龙江大学,2012.(LiJiangyou.StudyonBinocularVisionPositionandAttitudeEstimationAlgorithm[D].Harbin:HeilongjiangUniversity,2012.)
[11] 李爽.着陆小行星的视线测量自主光学相对导航算法及其可观性分析[D].哈尔滨:哈尔滨工业大学,2007.(LiShuang.StudyonOpticalMeasurementBasedRelativeNavigationandItsApplicationinPlanetaryLanding[D].Harbin:HarbinInstituteofTechnology. 2007. )
[12] 付梦印.Kalman滤波理论及其在导航系统中的应用[M]. 北京:科学出版社, 2010.
An Integrated Relative Navigation Algorithm for Spacecraft Based on Binocular Vision and Inertial Measurement
Zhao Yilun1,Qiao Bing1,Jin Yongqiang2,Yu Feng1
1. Nanjing University of Aeronautics and Astronautics,Nanjing 210000,China 2. Shanghai Institute of Aerospace System Engineering,Shanghai 201100,China
Bytakingthedualquaternionasamathematicaltool,anewrelativenavigationmethodforspacecraftbasedonmachinevisionandinertialnavigationispresented.Firstlythespacepositionandattitudemodelofdualquaternionisintroduced,andnextbinocularvisionmeasurementmodelisestablishedbasedoncollinearprojectionprincipletoprovideobservationdataforthesystem.Then,thestateequationofspacecraftisdeducedregardingthespacecraftkinematicsmodelandtheextendKalmanfilterisdesignedonward.Finally,thecomputersimulationisimplementedandtheresultsshowthattherelativeposition,attitudeandvelocityofthespacecraftarewellestimated.Therequirementsofspacemissionsuchasrendezvousanddockingandspacecraftcapturecanbemetbyusingthemethod.
Binocularvision;Integratedrelativenavigation;Dualquaternion; Kalmanfilter;Spacecraft
*上海航天创新基金资助项目(SAST201308);国家自然科学基金资助项目(61203197)
2015-10-10
赵逸伦(1991-),男,兰州人,硕士研究生,主要研究方向为空间在轨服务;乔 兵(1967-),男,江苏镇江人,副教授,主要研究方向为空间在轨服务;靳永强(1981-),男,山西榆次人,高级工程师,主要研究方向为空间安全;郁 丰(1980-),男,南京人,副研究员,主要研究方向为微小卫星导航与控制技术。
V448
A
1006-3242(2016)04-0047-06

