一种用于航天器交会任务的联合控制方法*

苏 晏 胡海霞 陈长青 王 敏

1.北京控制工程研究所, 北京 100190 2.空间智能控制技术国家级重点实验室，北京 100190



一种用于航天器交会任务的联合控制方法*

苏 晏1,2胡海霞1,2陈长青1,2王 敏1,2

1.北京控制工程研究所, 北京 100190 2.空间智能控制技术国家级重点实验室，北京 100190

空间交会轨迹设计是交会任务的重要内容。文中分析了变轨过程中轨道执行精度误差和姿态控制精度误差对控制效果产生的影响，综合考虑了相位调节燃料消耗和交会终端精度问题，给出了一种交会任务中特征点和Lambert多脉冲联合控制方法。通过两组不同初始轨道参数的联合控制仿真算例验证了该方法的有效性。 关键词 空间交会；控制误差；特征点变轨；Lambert变轨

空间交会和空间对接属于航天器轨道控制和姿态控制的范畴。空间交会是指目标航天器在不做机动的轨道上飞行，追踪航天器执行一系列轨道机动，与目标航天器在空间轨道上按预定轨道和时间相会的过程。交会的预定位置范围随空间交会目的的不同有不同规定，如以目标航天器为中心，若干公里为半径的球形范围[1]。空间拦截也是空间交会的一种任务形式。

空间交会技术是航天领域一个重要的研究和发展方向，具有较高的经济和战略价值。俄罗斯对交会对接模式已研究多年，其关键技术已在载货与载人飞船中实现应用。大距离空间拦截任务对交会时间、燃料消耗和交会精度提出了一系列条件约束。

交会路径规划指标主要体现在燃料消耗要求、交会时间要求和任务目标精度要求等几个方面。具体任务路径规划以任务编排规划初始条件和终端条件为边界输入条件，确定具体飞行阶段最优控制律，进行标称路径规划，并在实际飞行任务中修正实时路径。实际任务过程中考虑追踪器是空间交会任务的执行体，要充分考虑推进剂容量、发动机参数和分系统对太阳光照约束等追踪航天器系统性能和参数[2]。美国的DART计划在最后阶段失败正是由于交会操作消耗过多推进剂导致。

文献[3]基于摄动轨道动力学模型建立复杂条件约束下燃料最省调相轨道设计模型,得到调相轨道参数,实现小推力轨道设计。文献[4]针对航天器多冲量最优变轨问题给出一种遗传算法与序列二次规划算法结合的混合优化算法。文献[5]针对共面圆轨道目标大机动过程模型，分析在轨服务飞行器转移过程相位调整和能量需求，为接近目标机动策略选择提供参考。以上文献建立轨道模型，重点关注轨道调节过程中调相能力和燃料消耗，具有很高的参考价值。很多发射任务存在发射交会时间短，变轨任务调整空间小，对运载火箭的入轨误差敏感，对发射场和目标航天器间相位角要求高等问题，综合考虑燃料消耗、交会时间和交会终端精度等约束条件，本文提出特征点和兰伯特联合变轨交会方法[6-7]。

1 变轨精度影响分析

变轨过程中轨道执行精度误差、姿态控制精度误差都会对轨道控制效果产生影响，下文将分析影响误差的相关因素[8]。

1.1 发动机算法对半长轴精度变化的影响

实际轨道机动任务中需要根据轨道半长轴的增量需求确定轨道机动实施量级和实施方向，轨道机动计算过程中假设实施的机动为单点机动，实际轨道实施会引入一定执行误差[9]。

Fr沿卫星地心距方向，Ft在卫星的瞬时轨道平面内垂直于Fr指向卫星速度方向，卫星运行过程中处于三轴对地姿态稳定状态。半长轴变化量随推力变化如下：

(1)

近地点开机中，理想情况开机时刻集中在近地点：

(2)

真近点角度随相对近地点运行时间的展开函数如下：

(3)

对式(3)取第1项，分配到弧段时间内积分，并进行近似处理有：

(4)

定义比例因子为弧段时间内半长轴积分与理想开机情况半长轴增量比值如下：

(5)

选取Ft=1500，e=0.01，Δt=500，n=0.0012，第2项量级为e-004，量级很小。

对式(3)取前3项并进行近似处理有：

(6)

(7)

比例因子如下:

(8)

选取Ft=1500，e=0.01，Δt=500，n=0.001，第2项量级为e-004，量级很小。

由以上分析可知，由发动机弧段内开机引入的半长轴控制误差量级可以忽略。

1.2 姿态偏差对半长轴精度变化的影响

实际在轨轨道机动实施过程中姿态处于稳定状态，姿态控制和轨道控制同时进行，姿态控制精度会对轨道机动精度有一定影响。

轨道六要素与控制的关系如下：

(9)

假设变轨为理想近地点变轨，控制分量如下：

轨道面内半长轴要素变化如下：

(10)

取姿态控制在2°内，e=0.01，控制比例随真近地点角变化曲线如图1。

图1 控制比例变化图

由以上分析可知，姿态控制引入的半长轴控制误差量级可以忽略。

2 交会联合控制方法

2.1 交会技术

在交会对接的调相段需要基于摄动模型的非线性方程规划交会控制策略[10-11]。

交会对接调相阶段变轨目的是利用低轨道运动速度快的轨道特性减少2个航天器之间的相位角差，同时消除入轨时的轨道倾角偏差和升交点赤经偏差。调相变轨策略的选择在整个交会对接过程中有重要作用，控制精度影响最终交会任务的成败。

选取特征点变轨算法作为相对相位调节算法，迭代计算特征点轨道机动实施脉冲，相位调节过程中2个航天器轨道相互独立，轨道运行相位满足一定条件后引入Lambert多脉冲变轨策略，修正交会终端相对位置速度差。

2.2 特征点变轨

特征点变轨是共焦点椭圆轨道面内轨道转移能量最省的脉冲机动方式，轨道机动点一般在近地点、远地点、升交点和近拱点中综合选取。

远地点和近地点的选择不改变轨道平面和近拱点角距，速度增量能最大效能为轨道高度和偏心率做贡献，基于Kepler第三定律，半长轴决定轨道运行周期和轨道角速度，调整轨道高度可以调整追踪航天器和目标航天器相对相位角。升交点和近拱点的综合选取方式使速度增量能够最大效能为轨道倾角和升交点赤经的调整做出贡献。

由式(9)得到轨道倾角和升交点赤经调整公式如下：

(11)

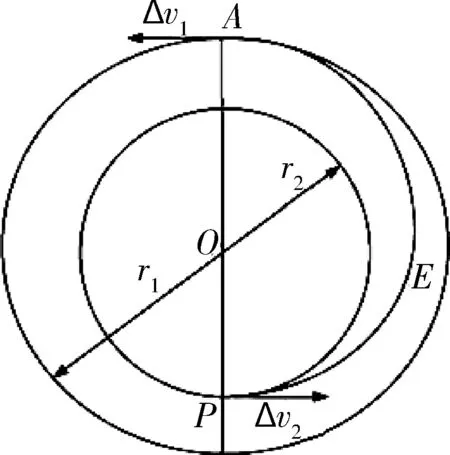
图2 特征点变轨示意图

特征点轨道机动包含n个轨道机动速度增量，选择设计变量、优化指标和约束条件如下：

(12)

式中，uf为追踪器和目标器期望达到的相位角差。

调相综合变轨算法如下：

1) 初值设定；

2) 仿真航天器运行到瞄准点，计算参考轨道和期望瞄准矢量Xaim；

3) 根据得到的速度增量仿真航天器到瞄准点X；

4) 得到仿真运行矢量和期望瞄准矢量误差脱靶量，设定边界条件，进入一定边界条件则退出循环，否则利用回到步骤3)进行迭代运算。

图3 算法流程图

2.3 Lambert变轨

由式(9)可以看出，特征点变轨机动对轨道要素的影响相互耦合，交会阶段后期引入Lambert多脉冲交会算法提高交会终端的相对位置速度精度[12-14]。

Lambert变轨是一个双脉冲问题，给定航天器初始时刻位置速度信息和终端时刻位置速度信息。给定转移时间，转移时间结束后航天器达到目标交会状态。模型测量误差、执行误差和轨道特性导致实际仿真过程中引入一定终端精度误差，采用多脉冲修正变轨算法进行修正。

Lambert问题本质是求解高斯问题，给定r1和r2，根据轨道特性选取转移时间t，由轨道特性得到追踪航天器初始速度信息，求解公式如下：

(13)

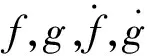
(14)

其中，u为目标器和追踪器真近点角差值。

建立如下方程，以ψ为迭代变量二分法求解方程。

(15)

考虑轨道特性，阶梯式选取Lambert脉冲实施点。

3 仿真算例分析

采用特征点变轨和Lambert多脉冲变轨联合算法策略，综合考虑时间和燃料消耗条件限制，机动脉冲设计选取过程中考虑轨道运行特性，选取两组目标器轨道参数算例，算例追踪时间不同，根据轨道特性设计脉冲实施时间。对2种工况进行仿真。轨道初始参数如表1。

表1 初始轨道参数

对2种工况进行特征点兰伯特联合变轨仿真，仿真过程中施加轨道机动速度增量如表2和3。

表2 工况1轨道机动惯性系下速度增量

表3 工况2轨道机动速度增量

仿真结束交会终端时刻相对位置速度误差如表4和5。

表4 交会终端相对位置状态

表5 交会终端相对速度状态

由仿真结果可以看出，特征点兰伯特联合变轨算法能在燃料消耗同时保证交会终端精度，变轨时刻点和变轨速度增量设计过程中需要充分考虑轨道特性和轨道约束情况。

4 结论

特征点变轨利用地轨道运动速度快的轨道特性减少2个航天器间的相位角，通过调节追踪器的轨道参数实现空间距离上的接近，特征点变轨以燃料消耗作为优化指标进行设计。Lambert变轨同时对轨道面内和轨道面外位置进行修正，以交会精度作为优化指标，交会时间和燃料消耗作为约束条件进行设计。

本文给出了特征点Lambert多脉冲联合变轨控制策略，以轨道特性为输入，任务燃料消耗、任务交会时间和任务交会精度为约束条件，实现了航天器高精度交会任务，为后续对接等任务需求提供高精度初始条件。

[1] 唐国金，罗亚中，张进. 空间交会对接任务规划[M].北京:科学出版社，2007.(Tang Guojin, Luo Yazhong, Zhang Jin. Space Rendezvous and Docking Mission Planning[M]. Beijing: Science Press, 2007.)

[2] 吴宏鑫，胡海霞，解永春，王颖. 自主交会对接若干问题[J]. 宇航学报, 2003,2(2):132-137.(Wu Hongxin, Hu Haixia, Xie Yongchun, Wang Ying.Several Questions on Autonomous Rendezvous Docking[J]. Journal of Astronautics,2003, 2(2): 132-137.)

[3] 王帅，尚海滨，崔平远，黄翔宇. 小推力地球卫星圆轨道同轨调相设计方法研究[J].宇航学报, 2013, 34(1) : 1-8.(Wang Shuai, Shang Haibin, Cui Pingyuan, Huang Xiangyu. Study on Method of Low-Thrust Phasing Maneuvers for Earth Circle-orbit Satellites[J]. Journal of Astronautics, 2013,34(1):1-8.)

[4] 付磊，安效民，覃曌华，徐敏. 基于混合遗传算法的多冲量最优变轨[J].航天控制, 2013, 31(3) : 15-19.(Fu Lei, An Xiaomin, Qin Zhaohua, Xu Min. The Optimal Multiple-impluse Orbit Transfer by Using Hybrid Genetic Algorithm[J].Aerospace control, 2013, 31(3): 15-19.)

[5] 李岩，姚静波，辛朝军，苏宪程. 在轨服务飞行器对共面圆轨道目标接近过程分析[J].航天控制, 2015, 33(4):1-11.(Li Yan, Yao Jingbo, Xin Chaojun, Su Xiancheng. The Approaching Process Analysis of On-Orbit Service Vehicle to Circular Coplanarity Orbit Target[J]. Aerospace control,2015, 33(4):1-11. )

[6] 周军. 面向制导律设计的目标信息估计方法研究[J]. 电子设计工程, 2014,22(14):164-167.(Zhou Jun. The Target Information Accurate Extraction for the Guidance Law Design[J]. Electronic Design Engineering,2014,22(14): 164-167.)

[7] Carson J M，Acikmese B ， Blackmore L， Wolf A A. Capabilities of convex Powered-Descent Guidance algorithms for pinpoint and precision landing[J]. IEEE Aerospace Conference, 2011, 83(6):1-8.

[8] Gergaud J, Haberkorn T. Orbital Transfer: Some Links Between the Low-thrust and the Impulse Cases[J]. Acta Astronautica, 2007, 60(8-9): 649-657.

[9] Senent J, Ocamp C Capella A. Low-thrust Variable-specific-impulse Transfers and Guidance to Unstable Periodic Orbits[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(2): 280-290.

[10] 佘志坤，薛白，丛源良，刘铁钢，郑志明. 最优双冲量交会问题的数学建模与数值求解[J]. 宇航学报, 2010, 1(1):155-161.(She Zhikun, Xue Bai, Cong Yuanliang, Liu Tiegang, Zheng Zhiming. Mathematical Modeling and Numerical Solving of the Optimal Two-Impulse Rendezvous Problem[J]. Journal of Astronautics, 2010, 1(1):155-161.)

[11] 李革非，宋军，刘成军. 交会对接任务轨道控制规划设计与实施[J]. 载人航天, 2014, 20(1):1-8.(Li Gefei, Song Jun, Liu Chengjun. Design and Implementation of Orbit Maneuver Programming in Rendezvous and Docking Missions[J]. Manned Spaceflight, 2014, 20(1):1-8.)

[12] Izzo D. Lambert′s Promble for Exponential Sinusoids[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(5): 1242-1245.

[13] 李生猛，朱战霞. 基于Lambert理论的多脉冲快速轨道交会研究[J].计算机仿真, 2009, 26(11): 80-83.(Li Shengmeng, Zhu Zhanxia. Research on Multiple-impulse Fast Orbital Rendezvous Based on Lamber Theory[J]. Computer Simulation, 2009, 26(11): 80-83.)

[14] 朱仁璋，蒙薇，胡锡婷. 航天器交会中的Lambet问题[J]. 中国空间科学技术, 2006, 12(6): 49-55.(Zhu Renzhang, Meng Wei, Hu Xiting. Lamert′s Problem in Spacecraft Rendezous[J]. Chinese Space Science and Technology， 2006, 12(6): 49-55.)

Combination Control Design for Rendezvous Task of Spacecraft

Su Yan1,2, Hu Haixia1,2, Chen Changqing1,2, Wang Min1,2

1. Beijing Institute of Control Engineering, Beijing 100190，China 2. National Laboratory of Space Intelligent Control，Beijing 100190，China

Thetrajectorydesignofspacerendezvousisanimportantcontentinspacerendezvoustask.Executionerrorduringorbitmaneuverandinfluenceofattitudecontrolerrorareanalyzed.Byconsideringseveralfactorsincludingfuelconsumptionduringphaseadjustmentandteminalprecision,multi-impulsecombinationcontroldesignisproposedforrendezvoustask.Thevalidityisshownbytwogroupsofdifferentinitialvaluesimulationsexamples.

Spacerendezvous;Controlerror;Special-pointmaneuvers; Lambertalgorithm

*国家自然科学基金资助项目(61304232，61403029)

2016-03-10

苏 晏(1987-)，女，河北人，硕士，工程师，主要研究方向为控制理论与控制工程；胡海霞(1977-), 女，河南人，硕士，高级工程师，主要研究方向为航天器控制与仿真技术；陈长青(1979-)，男，福建人，博士，高级工程师，主要研究方向为交会对接制导和控制；王 敏(1981-)，女，陕西人，博士，高级工程师，主要研究方向为航天器控制。

V526

A

1006-3242(2016)04-0042-05