卫星姿态控制系统的可重构性量化评价方法研究*
徐赫屿 王大轶 李文博
北京控制工程研究所,北京100190
卫星姿态控制系统的可重构性量化评价方法研究*
徐赫屿 王大轶 李文博
北京控制工程研究所,北京100190
控制可重构性本质上度量了不利条件下被控系统剩余的能控性。鉴于此,本文以卫星姿态控制系统为研究对象,研究了故障系统可重构性和剩余能控性之间的关系,提出了一种基于能控性格莱姆矩阵的可重构评价方法。首先,对标准能控性格莱姆矩阵的局限性进行了分析:由于该方法需要求解李雅普诺夫方程,故只适用于稳定系统或特征值和不为0的非稳定系统;然后,引入经验能控性格莱姆矩阵,不用直接求解李雅普诺夫方程即可获取格莱姆矩阵,使得该方法可扩展应用于卫星姿态控制系统;其次,考虑到经验格莱姆矩阵计算量大,采用精细积分方法提高了计算效率;最后,通过3个仿真算例,验证了本文所提方法的有效性和正确性。 关键词 卫星姿态控制系统;可重构性;经验格莱姆矩阵;精细积分
近年来,卫星在通信、对地观测、深空探测及军事等领域发挥着越来越重要的作用。随着空间技术的发展,对卫星姿态控制系统安全性和可靠性要求不断提高,故障重构方案的研究受到了广泛的重视。要实现对卫星控制系统的故障处理,首先系统自身必须是可重构的。可重构性的定义为[1]:在资源配置一定的情况下,系统发生故障后恢复全部或部分性能的能力。进行可重构性研究是提高卫星故障处理能力的根本所在。
目前,已有一些研究在理论上提出了控制可重构性的概念,并通过仿真算例验证其有效性和正确性。例如,文献[2]针对执行机构和传感机构的故障情况,将可重构性的概念引入卫星姿态控制系统,针对线性化的系统模型,利用能控性格莱姆矩阵的最小特征值给出了系统的可重构性度量指标;Frei等[3]研究了系统能控性和能观性格莱姆矩阵的行列式和线性定常系统可重构性的关系;Wu等[4]利用文献[5]提出的系统最小二阶模态值作为控制可重构性的度量指标,以此反映故障发生时故障系统的恢复能力,即控制可重构性通常可以由无故障系统的最小Hankel矩阵奇异值作为度量指标;Yang等[6-7]针对切换系统,定义了切换系统的格莱姆矩阵,并基于切换系统的格莱姆矩阵分析该故障系统的可重构性问题;Hoblos等[8]利用可恢复故障集的大小和不可恢复故障发生前的平均时间来评价故障系统的可重构性。
从现有文献中可以发现:目前研究多针对稳定系统和特征值和不为0的非稳定系统。这使得现有理论无法适用于卫星姿态控制系统。鉴于此,本文引入经验格莱姆矩阵。由于经验格莱姆矩阵不对系统矩阵的具体形式有要求,因此弥补了现有方法无法计算卫星控制系统能控性格莱姆矩阵的不足。为了简化计算,提高计算效率,提出利用精细积分计算系统的格莱姆矩阵的方法。本文分别对以上3种方法进行仿真验证并比较优缺点。即在已有理论研究的基础上,分析故障系统可重构性和剩余能控性之间的关系,给出了适用于卫星姿态控制系统的定量的可重构性评价方法。
1 问题的数学描述
考虑如下所求控制系统:
(1)
式中:A为系统矩阵;Bf(a)=[b1a1b2a2…
blal]T为系统故障后的控制矩阵,ai∈[0,1]为执行器失效因子,l为执行器个数;C为系统观测矩阵;x(t)为状态变量;u(t)为控制输入;y(t)为测量输出。
针对上述控制系统有如下命题和定义:
命题1 对于式(1)所示系统,若存在t1>t0,使得下式定义的能控性格莱姆矩阵
(2)
非奇异,则系统完全能控,反之亦然。其中,Φ(t0,t)为系统的状态转移矩阵。
定义1 定义性能指标
(3)
令:
J*=minJ(t1,x0,u(t)),J1=J(t1,x0,u1(t))
(4)
则控制能耗J*小于一个给定上界μ>0的一个充分条件是J1≤μ。

(5)

通过以上分析,可得到可重构性量化评价指标:
ρ=λmin(Wc)∈[0,+∞)
(6)
通过量化指标可以看出:可用ρ表征系统可重构性的大小,ρ越大,系统的可重构性越大,反之亦然。
2 基于格莱姆矩阵的可重构性评价
本节分析引入经验格莱姆矩阵,弥补了标准格莱姆矩阵方法存在的不足。同时,考虑到经验格莱姆矩阵计算量大,利用精细积分方法减小求解格莱姆矩阵的计算量,从而提高该方法的计算效率。
2.1 标准能控格莱姆矩阵的局限性分析
由可重构性指标ρ=λmin(Wc)的定义知,求得WC是得到可重构性指标的关键。又由式(1)所示系统能控性格莱姆矩阵的定义知:为得到能控性格莱姆矩阵WC,需求解李雅普诺夫方程[9]:
AWC+WCAT+BBT=0
(7)
换言之,求解标准格莱姆矩阵,即研究式(7)所示李雅普诺夫方程解的唯一性问题。
定理1 设A∈Rn×n,系统可重构性指标ρ=λmin(Wc)存在,即方程(7)存在唯一解,当且仅
λ(A)+λ(AT)≠0
(8)
其中,λ(A)为系统矩阵A的特征值。
证明:显然,σij=λi(A)+λj(AT),其中σij为[A⊗In]+[In⊗AT]的特征值。又方程(6)有解
⟺[A⊗In]+[In⊗AT]有唯一解
⟺[A⊗In]+[In⊗AT]非奇异⟺
σij=λi(A)+λj(AT)≠0。
证毕。
由定理1知,当系统含有和不为0的特征值时,可以直接通过系统能控性格莱姆矩阵的定义计算出系统能控性格莱姆矩阵,从而进一步研究系统基于能控性格莱姆矩阵的可重构性;反之则无法通过定义或求解李雅普诺夫方程(7)得到系统能控性格莱姆矩阵。
2.2 基于经验格莱姆矩阵的可重构性分析
针对2.1节标准格莱姆矩阵的局限性,本节引入经验格莱姆矩阵扩大了格莱姆矩阵适用范围,使得无论系统是否稳定,是否满足式(8)的要求,均可正确有效地计算系统能控性格莱姆矩阵,从而通过可重构性指标ρ对系统的可重构性进行评价与分析。
Lall[10]等人于1999年提出了经验格莱姆矩阵,并通过相应的数据即可完成系统能控性的计算[11],而对系统的线性/非线性属性和稳定/非稳定特性不做严格要求。
基本原理如下所述。首先,定义以下集合:
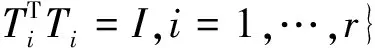
M={c1,…,cs│ci>0,i=1,…,s}
En={e1,…,ep}
(9)
式中:Tn为r个正交矩阵的集合;M是一个正常数集合;En为空间单位向量集合;r表示激励方向的矩阵数量;s表示在每个方向的不同激励大小的数量;p表示输入个数。
定义2[12]定义控制系统的经验能控格莱姆矩阵为:

(10)
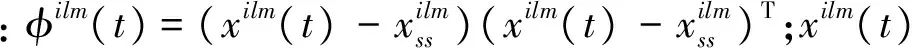
由定义2可以看出,经验格莱姆矩阵利用数值的方法正确有效地计算系统能控性格莱姆矩阵,从而避免了求解李雅普诺夫方程。
2.3 利用精细积分计算系统格莱姆矩阵
2.2节通过引入经验格莱姆矩阵,拓展了基于格莱姆矩阵的系统可重构性分析的适用范围。考虑到这种方法计算量大,计算效率降低,于是引入精细积分计算系统格莱姆矩阵[13-14]。该方法将精细积分的关键思想,即加法定理和增量存储直接应用于格莱姆矩阵的求解,给出了格莱姆矩阵的具体计算方法,高效地得到了其精确数值解。此外,这种方法不需要矩阵的求逆运算,当系统不稳定或者不满足式(8)时,同样可以高精度求解。
在计算如式(2)所示的能控性格莱姆矩阵时,将作用时间t分成时间步长为δ的一系列时间间隔。根据上式可得到任意时刻tk=kδ(k=0,1,2,…)和下一时刻tk+1=tk+δ的格莱姆矩阵之间,满足如下递推关系:
(11)
对式(11)中格莱姆矩阵的精细积分方法。首先根据精细积分的要点,推导其对应的加法定理,可得:


Wc(δ)+φ1(δ)Wc(δ)φ2(δ)
(12)
再将基本区段δ进行精细划分,设精细区段为ξ:ξ=δ/2N,然后合并得到结果。取N=20,当ξ非常小的时候,Wc(ξ),φ1(ξ)和φ2(ξ)用泰勒级数展开有限项进行近似。

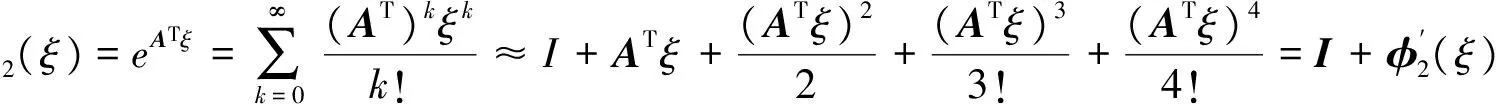

这样,在每一步的计算中,将主要注意力集中在增量,而不是全量上,避免了在合并时由于计算机的舍入操作引起的精度损失。
这一节内容具体阐述了用精细积分的方法计算系统的能控能性格莱姆矩阵,使得当系统不满足式(8)时,同样可以高精度求解。
3 仿真验证
下面分别用第2节提出的3种方法计算3类不同系统基于格莱姆矩阵的可重构性指标。
算例1:系统1的相关矩阵如下:


由计算结果知,该系统为稳定系统。下面分别用标准格莱姆矩阵、经验格莱姆矩阵和精细积分的方法计算该系统的可重构性,得到结果如图1~3所示。

图1 系统1的可重构性评价结果(标准格莱姆矩阵)
图2 系统1的可重构性评价结果(经验格莱姆矩阵)
图3 系统1的可重构性评价结果(精细积分)
图1~3横坐标分别表示执行机构a1和a2的故障情况,纵坐标表示了该故障系统随着执行机构a1和a2故障的变化,可重构性的变化情况。由图1~3知,随着执行机构故障模式的改变,系统的可重构性指标也将发生变化。3个仿真结果相同。
算例2:系统2的相关矩阵如下:


由计算结果可知,该系统为特征值和不为零的非稳定系统。分别用传统的标准格莱姆矩阵、经验格莱姆矩阵和精细积分的方法计算该系统的可重构性,得到结果如图4~6所示。

图4 系统2的可重构性评价结果(标准格莱姆矩阵)

图5 系统2的可重构性评价结果(经验格莱姆矩阵)

图6 系统2的可重构性评价结果(精细积分)
由图4~6可知,3个仿真结果重构结果相同。
算例3:以卫星姿态控制系统为例,该控制系统状态空方程如式(1)所示,式中,系数矩阵A3,B3f,C3分别为:
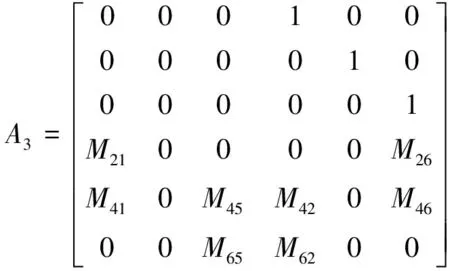
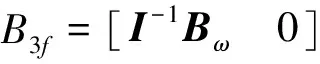

包含的计算公式为:
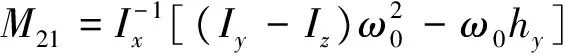


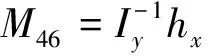


通过计算可知系统3为非稳定系统且含有和为0的特征值,故无法用传统的标准格莱姆矩阵计算系统的可重构性。分别经验格莱姆矩阵和精细积分的方法对该卫星姿态控制系统进行仿真,得到结果如图7和8所示。
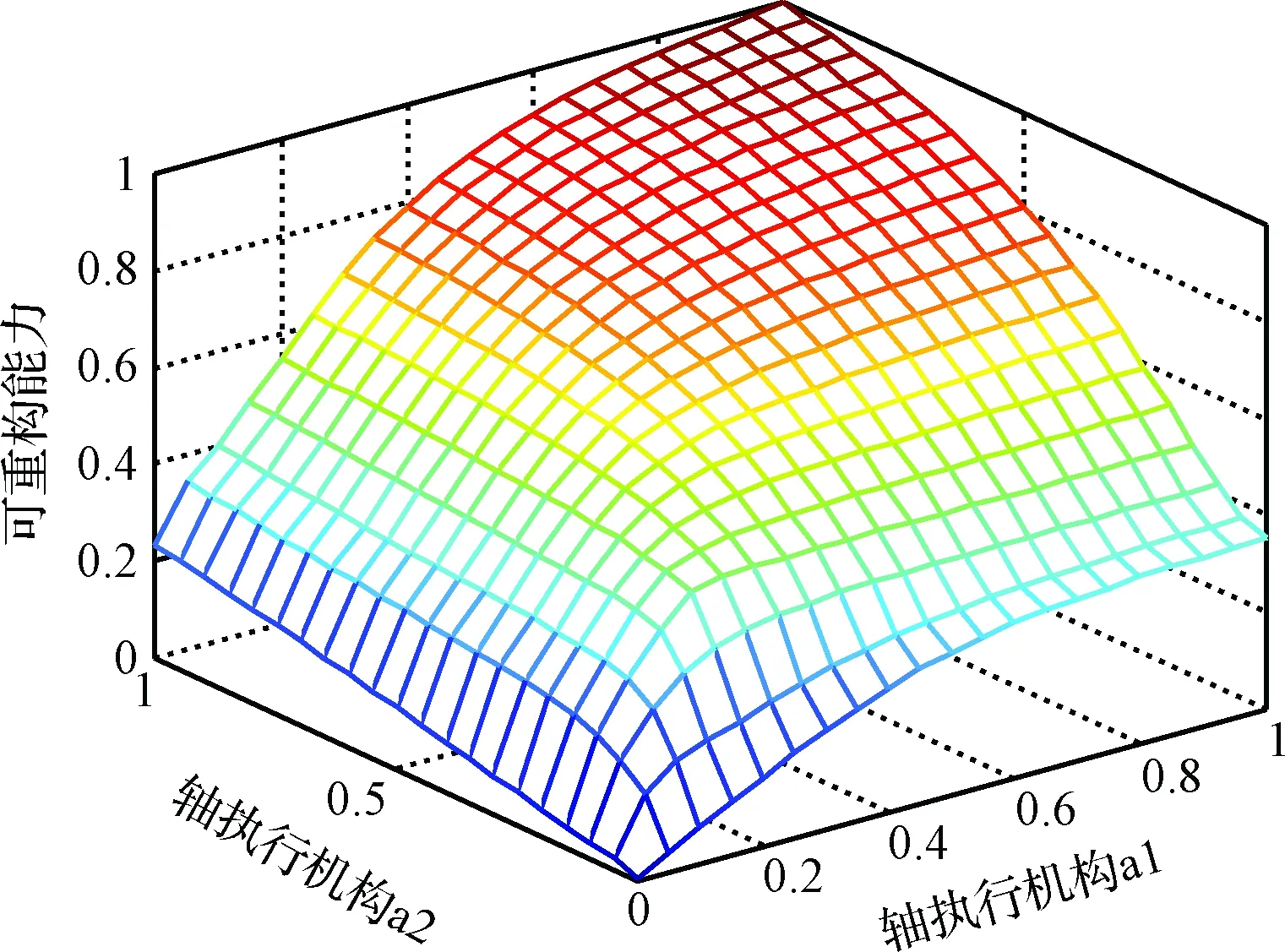
图7 系统3的可重构性评价结果(经验格莱姆矩阵)
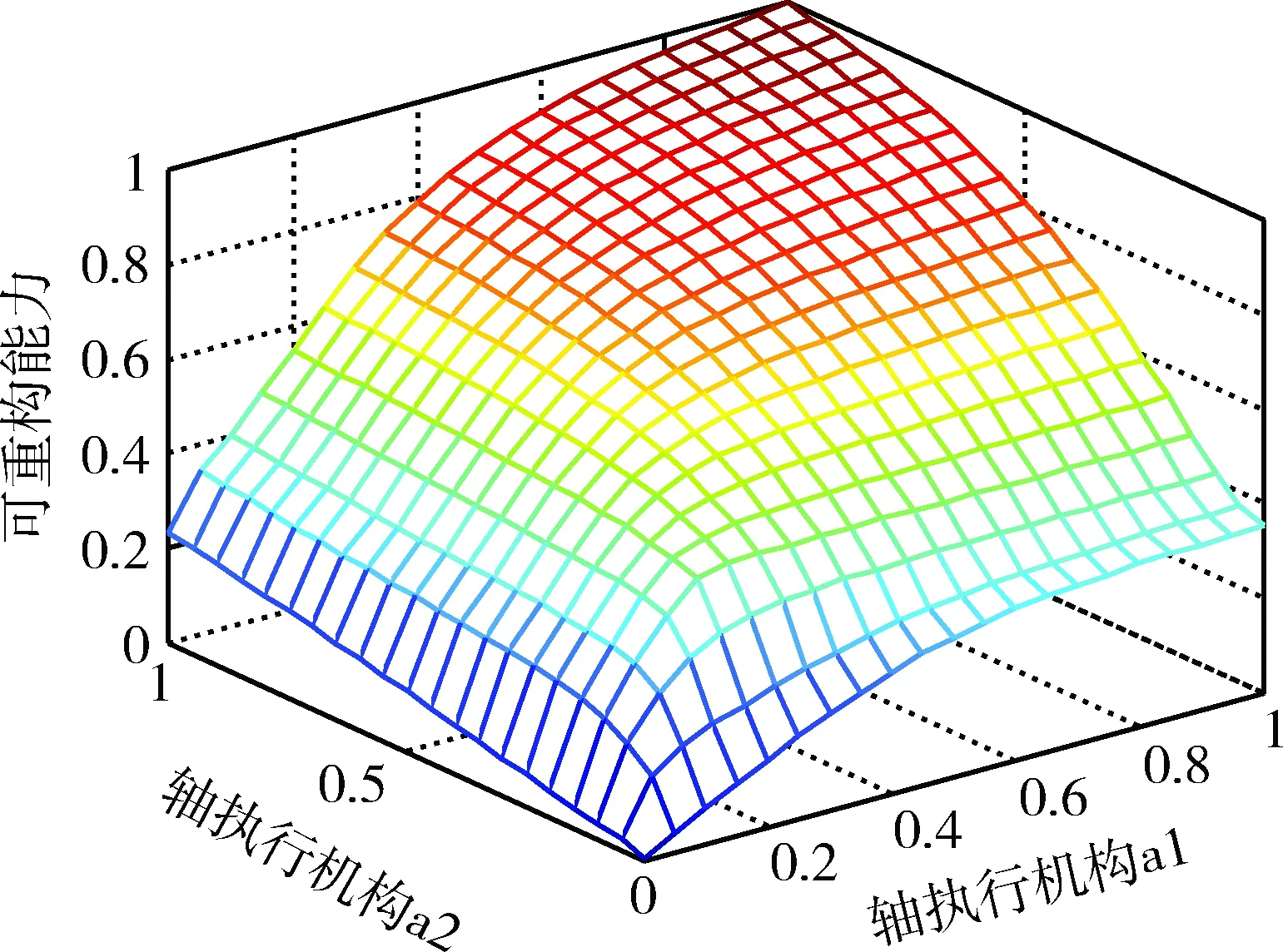
图8 系统3的可重构性评价结果(精细积分)
由图7~8可知,随着执行机构故障模式的改变,系统的可重构性指标也将发生变化。并且2个仿真结果重构结果相同。最后,统计3种方法计算基于系统能控性的可重构性所用时间如表1所示。

表1 三种基于系统能控格莱姆矩阵的可重构性评价方法所需时间
由表1可知,精细积分方法相对于标准格莱姆矩阵方法适用面广;相对于经验格莱姆矩阵方法计算时间短,计算效率大大提高,具有一定优越性。综上所述,3种基于系统能控格莱姆矩阵的可重构性评价方法优缺点比较如表2所示:

表2 三种基于系统能控格莱姆矩阵的可重构性
4 结论
解决了现有方法不适用于计算卫星控制系统的能控性格莱姆矩阵的问题。主要研究内容如下:
1)分析了故障系统的可重构性与剩余能控性之间的关系,给出了系统基于标准能控性格莱姆矩阵定量的可重构性评价的方法和该方法的局限性;
2)针对标准格莱姆矩阵的局限性,引入了经验格莱姆矩阵,突破了对系统线性性质、稳定性等的限制;
3)考虑到经验格莱姆矩阵计算量大,计算效率低,引入精细积分的方法简化了计算,提高了计算效率。
[1] Wu N E, Zhou K, Salomon G. Control Reconfigurability of Linear Time-invariant Systems[J].Automatica, 2002, 36(11):1767-1771.
[2] 樊雯, 程月华, 姜斌,等.卫星姿态控制系统的可重构性分析[J].宇航学报, 2014, 35(2):185-191.(Fan Wen, Cheng Yuehua, Jiang Bin, Liu Wenjing. Reconfigurability Analysis for Satellite Attitude Control Systems[J]. Journal of Astronautics, 2014, 35(2):185-191.)
[3] Frei C W, Kraus F J, Blanket M. Recoverability Viewed as a System Property[C]//European Control Conference. 1999.
[4] Wu N E, Zhou K, Salomon G. Control Reconfigurability of Linear Time-invariant Systems[J]. Automatica, 2000, 36(11):1767-1771.
[5] Moore B C. Principal Component Analysisi in Linear Systems: Controllability, Observability, and Model Reduction [J]. IEEE Transaction on Automatic Control, 1981, 26: 17-32.
[6] Staroswiecki M. On Fault Recoverability of a Class of Switched Systems[C]. The 29th Chinese Control Conference, Beijing, China, 2010: 4052-4056.
[7] Hao Yang, Bin Jiang, Marcel Staroswiecki. Fault Recoverability Analysis of Switched Systems [J]. International Journal of Systems Science, 2012, 43(43): 535-542.
[8] Hoblos G, Staroswiecki M, Aitouche A. Fault Tolerance with Respect to Actuator Failures in LTI Systems[C]//IFAC Safeprocess. 2000: 804-809.
[9] Zhou Kemin, Salomon Gregory, Wu Eva. Balanced Realization and Model Reduction for Unstable Systems [J]. International Journal of Robust & Nonlinear Control, 1999, 9(3):183-198.
[10] Lall S, Marsden J E, and Glavaski S.Empirical Model Reduction of Controlled nonlinear Systems[C]//in Peoc. 14th IFAC World Congr. Beijing, China, 1999: 473-478.
[11] Zhao H S, Xue N, Shi N. Nonlinear Dynamic Power System Model Reduction Analysis Using Balanced Empirical Gramian[J]. Applied Mechanics & Materials, 2013, 448-453:2368-2374.
[12] Zhao H, Xue N, Shi N. Empirical Gramian Balanced Reduction of Nonlinear Power System Model[J]. Electric Power Automation Equipment, 2014.
[13] 李素兰, 任元昊, 保宏,等. 时不变系统格莱姆矩阵的精细积分[J]. 西安电子科技大学学报:自然科学版, 2014, (06):106-110.(Li Sulan, Ren Yuanhao, Bao Hong, Zhang Wei. Precise Integration Method for the Gram Matrix of Time-invariant Systems[J]. Journal of Xidian University(Natural Science), 2014 (06):106-110.)
[14] 谭述君, 钟万勰. 基于精细积分的(最优)控制系统设计程序包[J]. 计算机应用与软件, 2007, 24(9):165-169. (Tan Shujun, Zhong Wanxie. Optimal Control System Design Toolbox Based on Precise Integration Method[J]. Computer Applications and Software, 2007, 24(9):165-169.)
[15] 胡宇桑, 王大轶, 刘成瑞. 卫星姿控系统可重构性综合评价方法研究[J]. 宇航学报, 2015, 36(5): 549-556.(Hu Yusang, Wang Dayi, Liu Chengrui. Reconfigurability Comprehensive Evaluation for Satellite Attitude Control System[J]. Journal of Astronautics, 2015, 36(5): 549-556.)
[16] Gonzalez B, Theilliol D, Sauter D D J. On-line Reconfigurability Evaluation for Actuator Faults Using Input/output Data[C]//Fault Detection, Supervision and Safety of Technical Processes. 2009: 674-679.
[17] 黄琳.系统与控制理论中的线性代数[M].北京:科学出版社,1984:606~682.
[18] Zhang J, Welch G, Bishop G, et al. Optimal PMU Placement Evaluation for Power System Dynamic State Estimation[C]// Innovative Smart Grid Technologies Conference Europe (ISGT Europe), 2010 IEEE PES. IEEE, 2010:1-7.
A Reconfigurability Evaluation Method for Satellite Control System Based on Gramian Matrix
Xu Heyu, Wang Dayi, Li Wenbo
Beijing Institute of Control Engineering, Beijing 100190,China
Thereconfigurabilitymeasuredresidualcontrollabilityundertheadverseconditionsinnature.Therefore,thispaperresearchestherelationshipbetweenreconfigurabilityandtheresidualcontrollabilityoffaultsystem.ThispaperaddressestheproblemofreconfigurabilityevaluationforsatellitecontrolsystemsbyGramianmatrix.Firstofall,weanalyzedthelimitationsofstandardcontrollabilityGramianmatrix.Thismethodisonlyapplicabletostablesystemandunstablesystemwithoutrootssumtozero.Second,inordernottosolvetheLyapunovequation,weintroducedempiricalGramianwhichmakeitcanbeappliedtosatellitecontrolsystemswithoutsolvingtheLyapunovequationandexpanditapplication.Andthen,becauseofthelargeamountofcalculationandlowefficiency,weproducepreciseintegrationmethodtoimprovetheefficiency.Finally,theefficacyoftheproposedmethodistestedthroughanumericalsimulation.
Satellitecontrolsystems;Reconfigurabilityevaluation;EmpiricalGramianmatix;Preciseintegration
*国家杰出青年科学基金(61525301);国家自然科学基金(61203093,61573060)
2016-04-25
徐赫屿(1990-),女,北京人,硕士研究生,主要研究方向为航天器可重构性评价;王大轶(1973-),男,黑龙江人,博士,研究员,主要研究方向为航天器制导、导航与控制,卫星可重构性及可诊断性评价与设计;李文博(1984-),男,天津人,博士,工程师,主要研究方向为航天器可诊断、可重构性评价与设计。
V448
A
1006-3242(2016)04-0029-07

