应用红外相机监测结果估计小型啮齿类物种的种群密度

李欣海, 于家捷, 张　鹏, 朴正吉, 肖治术

1 长白山科学研究院,延边朝鲜族自治州　133613 2 中国科学院动物研究所,北京　100101 3 东北林业大学野生动物资源学院, 哈尔滨　150040



应用红外相机监测结果估计小型啮齿类物种的种群密度

李欣海1,2,*, 于家捷2, 张鹏3, 朴正吉1, 肖治术2

1 长白山科学研究院,延边朝鲜族自治州133613 2 中国科学院动物研究所,北京100101 3 东北林业大学野生动物资源学院, 哈尔滨150040

摘要:红外相机(或称相机陷阱)技术可以提供物种组成、种群数量和行为等信息,广泛应用于野生动物的监测与管理。对于可以个体识别的物种,红外相机结合标志重捕法可准确估计其种群密度。但对于不可个体识别的动物,目前尚无成熟方法来估计其种群密度。建立了一个新方法,通过模拟个体运动并匹配红外相机监测数据来估计动物的种群密度。在长白山国家级自然保护区25hm2森林动态监测样地中,以每公顷一台的密度布设红外相机,调查小型啮齿动物的种群数量。在2011年和2012年冬季分别监测41d和40d。然后,设计模型模拟不同密度下啮齿类物种的运动过程,同时记录它们在25hm2的区域内被25台相机拍摄的次数。应用随机森林算法建立回归模型来匹配模拟结果与监测结果,估计啮齿类物种在样地内的密度及其置信区间。这是一种全新的利用红外相机监测数据估计种群密度的方法,可以填补对不可个体识别物种密度估计方法的空缺。

关键词：森林动态监测样地；红外相机；种群密度；运动模式；随机森林；啮齿类；长白山国家级自然保护区

近年来,红外相机技术在国内外野生动物监测研究中得到越来越广泛的应用[1- 4]。该技术可以直接提供动物在相机位点的种群密度信息。然而,要准确了解动物在一个区域的种群密度,需要建立模型进行估计。

目前有两种模型可以计算野生动物的种群密度：直接估计模型和间接估计模型。(1)直接估计模型：即根据监测结果(各位点的照片数)直接计算种群密度。标志重捕法是直接估计模型中最常用的方法,可准确估计可个体识别动物(如虎、豹等)的种群密度[5- 7]。对于难以个体识别的动物(如有蹄类物种、啮齿类物种等),目前还没有比较完善的方法来估计其种群密度[6,8]。(2)间接估计模型：即通过物种分布与环境变量的关系,利用物种分布模型估计物种在生境中的密度。物种的分布与植被、海拔、气候和人类干扰等因素密切相关。这些环境变量具有空间异质性,于是种群密度也具有相应的空间异质性。可以依据环境变量进行种群密度估计的物种分布模型很多,有广义线性模型(如逻辑斯蒂回归)、广义可加模型、分类树、神经网络、随机森林和占域模型(occupancy model)等[9-10]。这些模型的准确程度取决于物种对环境的依赖程度。对于狭域分布(只在特定海拔、植被等条件下分布)的物种,物种分布模型有时非常准确；对于广域分布、适合多种生境的物种,这些模型往往不很准确[9]。一般而言,直接估计方法不依赖于环境变量,可通过监测结果直接计算种群密度,比物种分布模型这种间接估计方法更适用。

目前最好的直接估计模型是Rowcliffe等设计的随机相遇模型(random encounter model)[6]。该模型假设动物像气体分子一样随机运动,并认为动物与相机的接触率(拍到的照片数)同动物的种群密度、运动速度、相机布设的时间、相机监测的面积呈正比。目前,该随机相遇模型已被其他学者采用来估计个体难以识别物种的种群密度[11-12]。然后,Rowcliffe等进一步估计了监测率同相机与动物间距离的关系,即量化了动物触发相机的概率随着距离的增加而降低的程度,进一步优化了随机相遇模型[13]。

随机相遇模型假设动物个体随机运动,并且同其他个体的运动无关[8,14]。这种理想化的假设往往与现实有较大的距离[8]。大多数动物主要在其家域内活动[15],动物个体之间的关系常十分密切。一些动物常集群活动,而另一些动物的个体之间存在竞争性地趋避行为。因此,动物的运动不是随机的,环境因素和个体(或群体)因素等都会影响到动物运动的方向和速度[16]。所以,对于大多数物种,随机相遇模型算出的种群密度并不可靠[8]。

近年来,许多调查人员已经积累了大量的红外相机监测照片。调查者经常面临的情况是有的相机重复拍摄了大量同一个体的照片,而有的相机没有拍到任何动物(虽然周围有明显的动物活动痕迹)。在这种情况下,Rowcliffe等的方法也是不适用的。缺乏可靠的种群密度估计方法,已经成为限制红外相机监测发挥更大作用的关键因素。

为了准确估计不可个体识别物种的种群密度,通过定义动物的运动模式(包括速度、活动范围和方向性等参数)来模拟不同密度下动物运动中被相机拍摄的过程,建立模型量化种群密度与照片数的关系；进而匹配模拟的照片数和野外红外相机的照片数,最后得到种群密度的估计值和置信区间。该模型考虑个体的领域范围和行为特征,真实反映动物的活动情况和被拍摄的概率,能够很好地区分反复被拍摄的个体和偶尔被拍摄的个体,将极大地提高种群密度估计的准确性,并有助于提高野生动物的监测和管理水平。

1研究方法

在长白山国家级自然保护区25hm2森林动态监测样地内,布设红外相机来调查啮齿动物和其它动物,汇总了每个相机拍摄到动物的照片数。然后模拟不同数量的动物个体在这个样地中的运动,获得模拟相机所拍摄到动物的照片数。通过建立一个机器学习模型比较实际监测和模拟数值,便可以估计动物在样地内的实际密度。

1.1红外相机监测

1.2对动物运动的模拟

通过定义一个个体的起始点、每次移动的方向、每次移动的步长和整个运动过程的步数模拟该个体的运动。起始点(时间t=0)是红外相机监测样方内任意选取的一点(X0,Y0)。第一步的运动方向为360°内的随机值θ。在时间t+1时动物的位置如下：

Xt+1=Xt+St+1×cox(θt+b)

Yt+1=Yt+St+1×sin(θt+b)

式中,S(t+1)为步长,是均值为M、标准差为σ1的正态分布的随机数；θ(t)为时间t时动物的运动方向。b为运动方向的偏转度数,是均值为0、标准差为σ2的正态分布的随机数。如果σ2接近于0,动物会直线运动；如果σ2较大,动物会进行随机游走(即布朗运动)。步数是一个与监测时间长度和物种活跃程度有关的常数,是时间t的最大值。

对于小型啮齿类物种,野外调查时发现了许多粪便、咬痕和足迹,对其活动范围和运动模式有粗浅的了解。模拟了不同参数时动物的活动轨迹(图1), 根据最接近的轨迹(图1左上的轨迹)确定了运动参数。参数值为：S=1m,σ1=0.1m,σ2=30°,步数为2000(假定每个个体每天在地面上运动50m,40d共2000m)。

借鉴Preisler等的理念[17],在研究区域内定义了一个量化生境适宜性高低的潜在曲面(potential surface)。假定起始点是该个体的巢穴洞口,该个体距洞口越远,越倾向于返回洞口,返回的概率为d/50。d为该个体到洞口的距离。当距离为50m时,该个体以100%的概率向洞口运动。

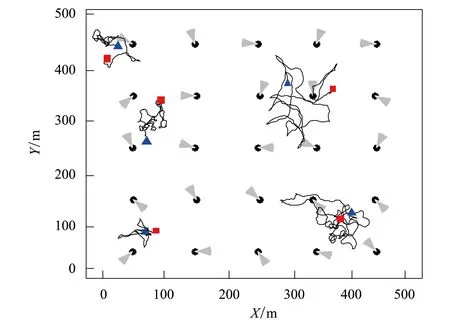
图1　在500米×500米的样方中模拟的红外相机监测区域(灰色面积)和5个动物的活动轨迹Fig.1　The monitoring areas (grey areas) and simulated movement tracks (five footprint chains) of five animals in the 500 m×500 m plot蓝色三角为起始点,红色正方形为终结点

1.3对相机监测的模拟

在模拟中,25台相机以100m间隔排成5行5列。每个相机有一个随机给定的监测方向。LTL5120相机的视角宽度为40 °。监测距离与动物的大小有关。对于花鼠(体长11—15cm),监测距离为5m；大林姬鼠体型较小(7—12cm),监测距离为3m。监测区域为一个锥形的区域,只有样方面积的0.0013% (大林姬鼠)和0.0035%(花鼠)(图1)。每当一个个体在一个相机的监测区域中出现时,该相机便增加一个记录。模拟了样方中有1—100个个体时25台相机的记录数。模拟次数为50次。

1.4匹配相机监测和模拟的结果

通过50次模拟的结果建立数据集,形成5000行×26列的表格,其中第一列为个体数量,取值为1—100,重复了50次；第2—26列为25个相机记录到的照片数。动物个体数量与25个相机的照片数呈正相关,但不是简单的线性关系,它受到动物个体的起始点位置、运动模式和相机朝向的影响。通过随机森林(random forest)的算法构建一个机器学习模型,用来建立动物个体数与相片数的关系。随机森林是一种基于分类树(classification tree)的算法[18]。同神经网络等其他机器学习模型相比,随机森林的算法高效(运算速度快),预测精度在诸多模型中名列前茅[19-20]。随机森林对多元公线性不敏感,结果对缺失数据和非平衡的数据比较稳健,被誉为当前最好的算法之一[19]。它可以很方便地处理回归和分类等多种问题[21]。

2结果

2011年和2012年冬季有效相机分别为23台和20台,共计1743捕获日,共计录到小型啮齿类305次,其中花鼠148次,大林姬鼠129次,黑线姬鼠8次,以及不可识别的啮齿类或食虫类20次(图2)。由于黑线姬鼠记录少,下面主要就花鼠和大林姬鼠的数据进行分析。

图2　2011至2012年在长白山森林动态监测样地内应用红外相机监测到的小型啮齿类的位置和数量Fig.2　The camera locations and the number of records in the Changbaishan forest dynamics plot in the winter of 2011 and 2012图中黑色三角表示相机位置； 灰色圆的大小表示该相机拍摄到该物种的记录数的大小；每条记录用彩色的圆圈表示,暖色表示监测阶段的前期(前20d),冷色表示后期(后20d)

本文中模拟了样方中有1—100只个体时所拍摄到的相片数。在50次模拟中,每次模拟的结果都不相同。图3是其中一次模拟的结果,显示个体数为10—60只时的照片数。由于监测面积只有样方面积的0.0013%—0.0035%,因此有些个体没有被监测到。小型啮齿类的运动速度不快,活动区域较小,有的个体被反复拍摄到,照片记录数较高。

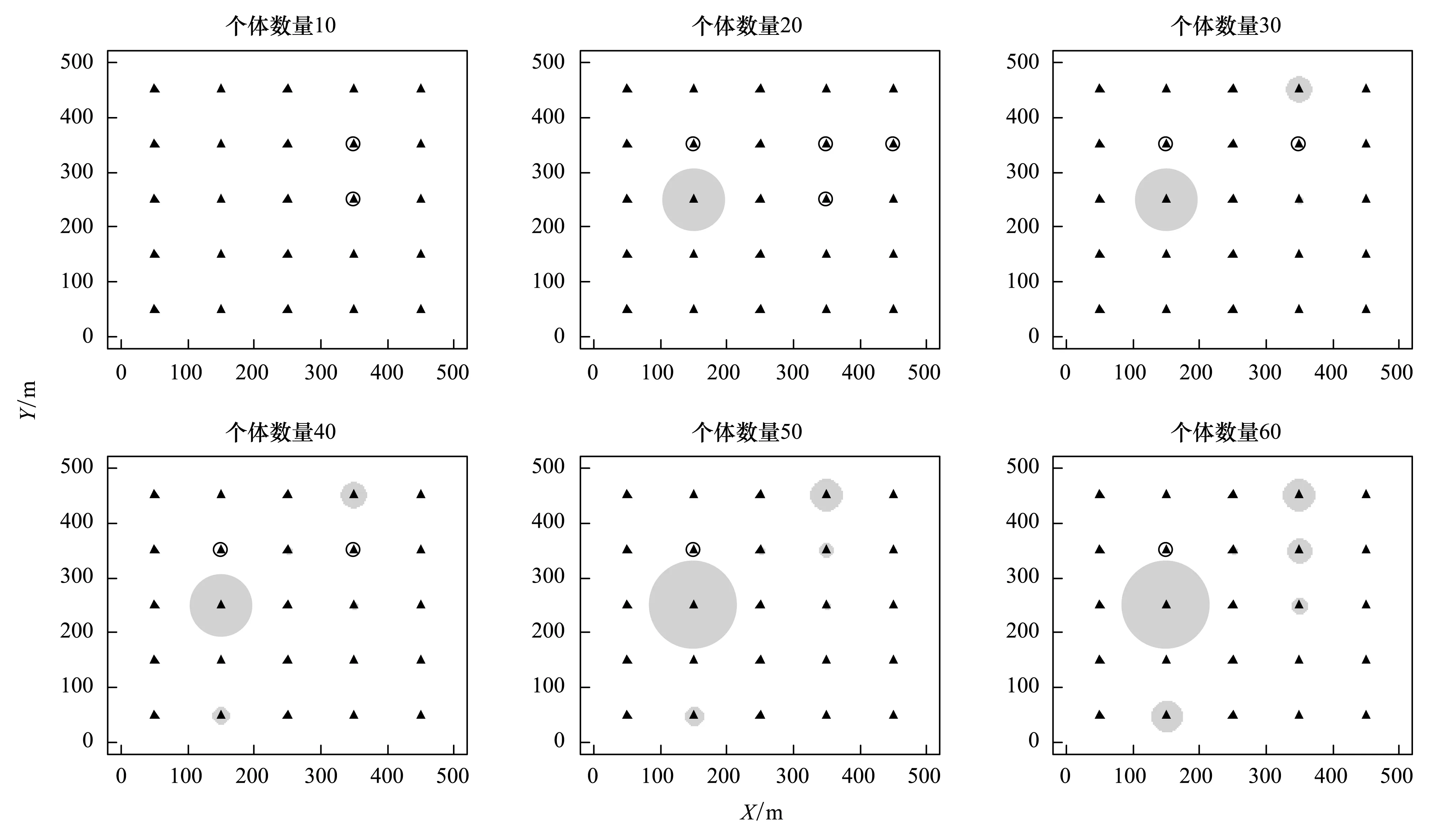
图3　随机模拟一个500m×500m的样地中监测到的花鼠的位置和数量Fig.3　The simulated camera trapping for Siberian chipmunk in a 500 m×500 m plot黑色三角表示相机位置；灰色圆的大小表示该相机拍摄到的物种记录数的大小；记录数小于3次(灰色圆的面积很小)时用圆圈表示

通过模拟1—100只动物随机运动时被相机拍摄的过程来建立数据集,汇总每个相机拍摄的照片数,并应用随机森林量化个体数同照片数的回归关系。该模型应用了1000个回归树,25个相机的照片数能够解释89.25%(对于花鼠)和91.3%(对于大林姬鼠)的种群密度(取值范围1—100),说明照片数和种群密度的对应性比较好。把实际监测数据(每个相机的照片数)(图2)带入模型,得到的估计结果如表1。2011年和2012年监测到的数量不同,花鼠的平均密度为1.96只/ hm2,大林姬鼠的平均密度是2.71只/ hm2。

3讨论

本文通过定义动物的运动模式(包括速度、活动范围和方向性等要素)来模拟不同密度时动物运动过程中被相机拍摄的频率,然后建立模型匹配模拟结果和红外相机的监测记录,进而得到种群密度的估计值和置信区间。该方法与以前通过红外相机估计种群密度的诸多方法都不相同。标志重捕法对于虎豹等可识别的物种非常有效,其密度估计的准确性取决于重捕率、个体的迁入和迁出率以及死亡率。对于不可识别的动物,Rowcliffe等的随机相遇模型[6,13]是简单易用的方法,在一些案例中是非常准确的[6]。然而,应用红外相机数据来估计某个物种种群密度的核心问题是如何区分反复被相机所拍摄的个体和偶尔被相机所拍摄的个体。我们的种群密度估计模型考虑到个体的领域范围和行为特征,是根据动物的行为学原理来估计密度的,能够很好地区分反复被拍摄的个体和偶尔被拍摄的个体。

表1通过红外相机和模拟动物运动相匹配的方法估计花鼠和大林姬鼠在长白山森林动态监测样地(25 hm2)内的数量

Table 1The Estimated abundance of Siberian chipmunk and Korean field mouse in the plot (25 hm2) for monitoring forest dynamics in the Changbai Mountain based on the movement simulation and camera trapping

年Year花鼠SiberianChipmunk/只大林姬鼠Koreanfieldmouse/只均值Mean置信区间Confidentinterval(95%)均值Mean置信区间Confidentinterval(95%)20116149—896549—9820123720—527161—90

基于运动模式和红外相机的密度估计方法需要的参数比较多。在本文中,主观地给定了动物的运动参数。研究者应该了解目标动物的行为特征(是在领域内随机运动,还是往返于觅食地和休息区等),领域大小、个体间的关系(单独或结群)、吸引和排斥动物的因素(食物资源、天敌、人为干扰等)；而本文只考虑了距离,即动物个体距离起始点(假定为洞口)越远,其返回的概率越大,由此保证动物个体只在其领域内活动。另外,假定花鼠和大林姬鼠有同样的领域范围和运动模式。随着研究的进展,将引入更多的参数,并对不同物种进行参数的细化。

红外相机的监测过程具有很高的不确定性。有的相机恰好布设在鼠洞口,记录到了大量的照片,而有的虽然也在动物的领域内,但由于偏离其活动轨迹,极少被拍摄到。应用本文的方法对动物种群密度进行估计,也有一定的随机性。本文给出的种群数量(表1)是多次模拟的平均值,并不一定是概率最高的值。比如在2011年长白山森林动态监测样地的监测中,估计的大林姬鼠数量为65只,然而数量为57只和71只的概率还要更高些(图4)。

图4　用个体运动模拟和红外相机监测相匹配的方法估计长白山森林动态监测样地内大林姬鼠的数量Fig.4　Estimating the abundance of Korean field mouse in the Changbaishan forest dynamics plot based on the movement simulation and camera trapping灰色曲线为大林姬鼠数量的概率密度函数,垂直实线为估计的数量,两侧的虚线为2.5%和97.5%分位数(表示95%的置信区间)

花鼠和大林姬鼠在不同的地区有不同的密度。在吉林省左家自然保护区的次生阔叶林生境中,花鼠的密度是29.78只/ hm2[22],这里花鼠是优势种,数量远高于其他鼠类[22]。长白山林区的花鼠密度比较低,只占鼠类总量的6.2%[23]。吉林省寒葱岭地区花鼠密度也比较低,占鼠类总量的15.85%[24]。长白山林区和吉林省寒葱岭地区大林姬鼠是优势物种[23-24]。在北京小龙门林场,花鼠的密度低于1.01只/hm2[25]。在监测的样方中,尽管花鼠和大林姬鼠是优势种,其密度都比较低。根据观察,样方内的鼠类密度低于周围样方外的鼠类密度。主要原因可能是该样方是森林动态监测样地,每年研究人员都进行大量的观测和调查,对动物造成了干扰。

本文的模拟和实际的监测还有许多不匹配的地方。在实际监测中,由于相机丢失和损坏,有数据的仅为23台(2011年)和20台(2012年),不足25台。另外,相机的位置与标准的等间距分布也不同。最重要的是相机的布设位点选择在动物痕迹多的地方,这样会过高地估计种群密度。另外。在40d的监测中,动物会有迁入、迁出和被捕食的情况。这些都会影响密度估计的结果。

用红外相机监测来估计动物种群大小,在空间范围上应该包含若干个个体(或群体)的领域。长白山森林动态监测样地500m×500m的空间范围,对于监测小型啮齿类比较合适。对于野猪、狍子等动物,需要3—10km2的监测范围才能比较准确地估计其种群密度。相机应该呈网格状布设,以便相对均衡地取样。有照片的和没有照片的相机信息都有价值,这些信息可以帮助我们估计动物的领域范围。

参考文献(References):

[1]Karanth K U. Estimating tigerPantheratigrispopulations from camera-trap data using capture-recapture models. Biological Conservation, 1995, 71(3): 333- 338.

[2]马世来, Harris R B. 自动感应照像系统在野生动物调查中的应用. 动物学研究, 1996, 17(4): 360- 360, 370- 370.

[3]马鸣, 徐峰, Chundawat R S, Jumabay K, 吴逸群, 艾则孜, 朱玛洪. 利用自动照相术获得天山雪豹拍摄率与个体数量. 动物学报, 2006, 52(4): 788- 793.

[4]李勤, 邬建国, 寇晓军, 冯利民. 相机陷阱在野生动物种群生态学中的应用. 应用生态学报, 2013, 24(4): 947- 955.

[5]Gardner B, Reppucci J, Lucherini M, Royle J A. Spatially explicit inference for open populations: estimating demographic parameters from camera-trap studies. Ecology, 2010, 91(11): 3376- 3383.

[6]Rowcliffe J M, Field J, Turvey S T, Carbone C. Estimating animal density using camera traps without the need for individual recognition. Journal of Applied Ecology, 2008, 45(4): 1228- 1236.

[7]Royle J A, Nichols J D, Karanth K U, Gopalaswamy A M. A hierarchical model for estimating density in camera-trap studies. Journal of Applied Ecology, 2009, 46(1): 118- 127.

[8]Foster R J, Harmsen B J. A critique of density estimation from camera-trap data. The Journal of Wildlife Management, 2012, 76(2): 224- 236.

[9]Li X H, Wang Y. Applying various algorithms for species distribution modelling. Integrative Zoology, 2013, 8(2): 124- 135.

[10]Guisan A, Zimmermann N E. Predictive habitat distribution models in ecology. Ecological Modelling, 2000, 135(2/3): 147- 186.

[11]Manzo E, Bartolommei P, Rowcliffe J M, Cozzolino R. Estimation of population density of European pine marten in central Italy using camera trapping. Acta Theriologica, 2012, 57(2): 165- 172.

[12]章书声, 鲍毅新, 王艳妮, 方平福, 叶彬. 红外相机技术在鼠类密度估算中的应用. 生态学报, 2013, 33(10): 3241- 3247.

[13]Rowcliffe J M, Carbone C, Jansen P A, Kays R, Kranstauber B. Quantifying the sensitivity of camera traps: an adapted distance sampling approach. Methods in Ecology and Evolution, 2011, 2(5): 464- 476.

[14]Rowcliffe J M, Kays R, Carbone C, Jansen P A. Clarifying assumptions behind the estimation of animal density from camera trap rates. The Journal of Wildlife Management, 2013, 77(5): 876- 876.

[15]Börger L, Dalziel B D, Fryxell J M. Are there general mechanisms of animal home range behaviour? A review and prospects for future research. Ecology Letters, 2008, 11(6): 637- 650.

[16]Avgar T, Mosser A, Brown G S, Fryxell J M. Environmental and individual drivers of animal movement patterns across a wide geographical gradient. Journal of Animal Ecology, 2013, 82(1): 96- 106.

[17]Preisler H K, Ager A A, Wisdom M J. Analyzing animal movement patterns using potential functions. Ecosphere, 2013, 4(3), doi: 10.1890/ES12-00286.1.

[18]Breiman L. Random forests. Machine Learning, 2001, 45(1): 5- 32.

[19]Iverson L R, Prasad A M, Matthews S N, Peters M. Estimating potential habitat for 134 eastern US tree species under six climate scenarios. Forest Ecology and Management, 2008, 254(3): 390- 406.

[20]Cutler D R, Edwards T C Jr, Beard K H, Cutler A, Hess K T, Gibson J, Lawler J J. Random forests for classification in ecology. Ecology, 2007, 88(11): 2783- 2792.

[21]李欣海. 随机森林模型在分类与回归分析中的应用. 应用昆虫学报, 2013, 50(4): 1190- 1197.

[22]张克勤, 陈玉梅, 冯军, 张振华, 张长明. 次生阔叶林花鼠的种群生态. 东北林业大学学报, 2008, 36(11): 77- 79.

[23]刘国平, 任清明, 王峰, 蔡增林, 周旭. 吉林省长白山地区鼠类的调查研究. 中华卫生杀虫药械, 2007, 13(1): 46- 47.

[24]孙帆, 张殿仁, 邹天顺. 吉林省寒葱岭地区森林鼠类调查. 动物学杂志, 1993, 28(6): 20- 23.

[25]宋杰, 毕中霖, 张正旺, 潘超, 郭冬生, 张雁云. 北京小龙门林场夏季啮齿类的群落结构及其年变化. 北京师范大学学报: 自然科学版, 2001, 37(2): 255- 259.

Estimating population density of small rodents using camera traps

LI Xinhai1, 2,*, YU Jiajie2, ZHANG Peng3, PIAO Zhengji1, XIAO Zhishu2

1ChangbaiMountainAcademyofSciences,YanbianKoreanautonomousprefecture133613,China2InstituteofZoology,ChineseAcademyofSciences,Beijing100101,China3CollegeofWildlifeResources,NortheastForestryUniversity,Harbin150040,China

Abstract：Using camera traps can provide valuable information for estimating wildlife density, and further contributes to conservation activities. For species that can be individually recognized, such as tigers and leopards, camera trapping combined with mark-recapture techniques can provide reliable estimates of population density. However, most species cannot be individually recognized, and no sophisticated models are available for accurate estimation of their densities. At present, the only available model is Rowcliffe et al.′s gas molecule movement model, which assumes animals behave like ideal gas particles, moving randomly and independently of one another. Such a model is not appropriate for either territorial or social species, or elusive species that usually move along trails. We developed a novel method to estimate the population density of animals that cannot be individually recognized. This method is based on the simulation of animal movement and pseudo camera trapping processes at a series of population densities. We matched results of real camera trapping with those of simulated camera trapping to estimate population density. The method was coded using the R language. We deployed 25 cameras (LTL5120) in the 25 hm2 forest dynamics plot in the Changbaishan National Nature Reserve, China for 41 days in the winter of 2011 and 40 days in the winter of 2012. The Siberian chipmunk (Eutamias sibiricus)and Korean field mouse (Apodemus peninsulae) are two dominant species in the plot. Animal movement was simulated by setting a starting location and a series of moving directions and step lengths. The starting location was a randomly selected point in the survey area. The direction of the first movement, θ, was also randomly selected from a range of 0—2π. The length and angle of deflection of subsequent movements followed normal distributions N (1 m, 0.1 m) and N (0, 30 degrees), respectively. We also defined a home range for each species by forcing the simulated animal to return to the starting location (assumed to be a mouse hole) at a rate of D/50, where D is the distance in meters between the current and original locations. The simulations of animal movement were run under a series of population densities. We matched the simulated results and the observed photo records using the random forest algorithm to estimate the population density and its confidence intervals. This analysis determined that the density of the Siberian chipmunk is 1.96hm2, and 2.71hm2 for the Korean field mouse. Our method has a number of limitations. First, the movement pattern of the target species must be known. In this study, we selected movement parameters (step length, angle of deflection, home range size, etc.) by visually checking the simulated footprint chains, which should be replaced by field tracking. Second, the cameras must be deployed in the field systematically, at regular intervals, so that virtual camera trapping can be simulated accordingly. In spite of the limitations, this method can provide reliable estimates for population density for animals that cannot be individually recognized. Our new method can be used for other camera trapping practices, as long as the movement pattern of the species is known.

Key Words:forest dynamics plots; camera trap; population density; movement pattern; random forest; rodents; Changbaishan National Nature Reserve

基金项目:国家自然科学基金项目(31572287)；长白山科学研究院科研开放基金资助项目

收稿日期:2014- 11- 02;

修订日期:2016- 01- 05

*通讯作者

Corresponding author.E-mail: lixh@ioz.ac.cn

DOI:10.5846/stxb201411022142

李欣海, 于家捷, 张鹏, 朴正吉, 肖治术.应用红外相机监测结果估计小型啮齿类物种的种群密度.生态学报,2016,36(8):2311- 2318.

Li X H, Yu J J, Zhang P, Piao Z J Xiao Z S.Estimating population density of small rodents using camera traps.Acta Ecologica Sinica,2016,36(8):2311- 2318.