不同偏心度的环空涡动流场特性

张晋凯李根生黄中伟田守嶒宋先知王海柱. 油气资源与探测国家重点实验室；2. 中国石化石油工程技术研究院

不同偏心度的环空涡动流场特性

张晋凯1，2李根生1黄中伟1田守嶒1宋先知1王海柱1
1. 油气资源与探测国家重点实验室；2. 中国石化石油工程技术研究院

为了深入研究环空涡动时的流场特性，根据流体力学理论，以连续性方程和N-S方程为控制方程，利用计算流体力学技术对钻柱涡动时环空赫巴流体的流动进行了系统的数值模拟，研究了不同公转方向下钻柱偏心度的变化对环空切向速度剖面与合速度剖面的影响。通过对模拟数据的对比分析，发现不同公转方向下环空流场分布截然不同，正向公转时切向速度在环空宽间隙处随着公转速度、自转速度和偏心度增大正向增大；反向公转时会出现二次流，切向速度在环空宽间隙处随偏心度的减小整体反向减小，同时二次流趋势越明显，摩阻压耗越大。合理应用这些规律有助于完善现有钻井水力学理论，更好地揭示井下环空流场特性，并为钻井水力参数优化设计提供有效的理论指导。

涡动；环空；赫巴流体；摩阻压耗；数值模拟；流场

钻进过程中钻柱在井筒内一般会出现涡动，即在地面转盘带动下顺时针自转的同时还绕井眼轴线公转。涡动的出现以及公转的半径（即涡动时钻柱的偏心度）和方向（顺时针方向、逆时针方向）就目前钻井水平而言无法控制且很难预测，通过实验难以揭示其内部规律，最可行的方法是借助数值模拟技术进行研究［1-5］。因此研究涡动时的偏心度对由自转旋流场、公转旋流场和轴向流场叠加而成的环空真实流场［6-12］的影响有助于完善现有钻井水力学理论，更好地揭示井下环空流场特性，并为钻井水力参数优化设计提供理论指导［13-16］。

1 环空流动的建模与模拟Model building and simulation of flows in annulus

1.1钻井液模型

Model for drilling fluids

为更好地描述非牛顿不可压缩流体的流变特性，采用了更为合理的赫巴流变模式，该模式也可看作修正的幂律模式，具体方程为［17］

式中，τ为剪切应力，Pa；τHB为该模式的屈服值，Pa；K为稠度系数，Pa·sn；n为流性指数，无因次；γ为剪切速率，s-1。屈服值是钻井液的实际动切力。根据文献［18-19］内的具体数据，采用其中的一种油基钻井液的数据，回归出相应的赫巴模式的具体参数

1.2几何模型

Geometric model

数值模拟所涉及到的几何尺寸均采用现场实际尺寸，钻柱外径139.7 mm，套管内径244.0 mm，环空长度15 m，其他参数见表1。选取15 m长的环空钻井液作为研究对象，采用基于交错网格的SIMPLEC算法对连续性方程和N-S方程进行离散化，动量方程的对流项进行离散化时为保证计算精度，采用二阶格式；建立的网格几何模型如图1。

表1　环空流动几何参数Table 1 Geometric parameters for flows in annulus

设置3类边界类型：速度入口边界，压力出口边界以及旋转壁面边界，设定该边界绕其自身轴线自转的同时绕井壁轴线公转，井壁为静止壁面，所有壁面都简化为无滑移水力光滑的壁面，且近壁面处的网格加密划分，采用柱坐标系，对称轴为z轴，按照速度分量方式设定速度入口值［20］。

图1　不同偏心度下环空流体区域的几何网格模型Fig.1 Geometric grid model for flowing zones in annulus with various eccentricities

1.3流动模型

Flow model

将流体视为不可压缩流体，且具有一定的黏度值和密度值，不考虑传热和重力的影响［21］。用连续性方程和N-S方程共同描述环空流动，基于有限体积法的思想进行离散。由于涡动时的环空流场属于复杂的旋流场，流体质点脉动程度较高，因此采用湍流两方程模型中的Realizable模型，该模型能够有效地将湍动黏度模型中的系数与应变率耦合起来，能够更为精确地描述包括旋转均匀剪切流、包含有射流和混合流的自由流、管道内流动、边界层流动以及带有分离的流动。因此文中采用Realizable模型［22］。

1.4环空流动的数值模拟

Numerical simulation for flows in annulus

涡动时自转和公转坐标系都遵循右手准则，规定转盘自转为顺时针方向，以此作为旋转正方向，钻柱在井眼内的公转根据已有研究的描述有顺时针和逆时针2个方向，当公转为顺时针时，与自转方向一致，根据右手准则，为正向涡动，反之为反向涡动。

为更好地研究不同偏心度下流场的变化规律，设置其余钻井参数在合理范围，如表2。

表2　钻柱涡动时环空流动数值模拟参数设置Table 2 Parameters for numerical simulation of flows in annulus during drill pipe vortex

取15 m长偏心环空钻井液距入口9 m处横截面上沿对称轴的剖面进行分析，横坐标0表示井筒中轴线。

2 钻柱涡动时环空流场特性分析Features of flow field in annulus during drill pipe vortex

设井筒圆心为O1，钻柱圆心为O2，井筒半径为R，钻柱半径为r，偏心距为h，公转速度为ω1，自转速度为ω2，P1为最宽间隙处对应的钻柱外壁面位置，P2为最窄间隙处对应的钻柱外壁面位置。设图2中时刻的自转线速度方向为正方向，根据分析可知：

当自转与公转同向，P1点和P2点的线速度（切向速度）分别为

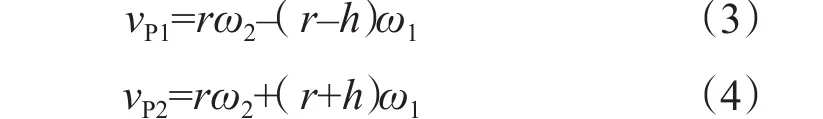
当自转与公转反向，P1点和P2点的线速度（切向速度）分别为

2.1偏心度对流速剖面的影响

Impacts of eccentricity on flow velocity profile

分析模拟数据发现，其他条件不变时，随轴向流速增大，环空内宽窄间隙处合速度剖面变化规律与一般环空流动相同，由于径向速度较小且变化不明显，本研究未作讨论。下面着重分析涡动时的偏心度及公转正反方向的变化对环空气场的影响。

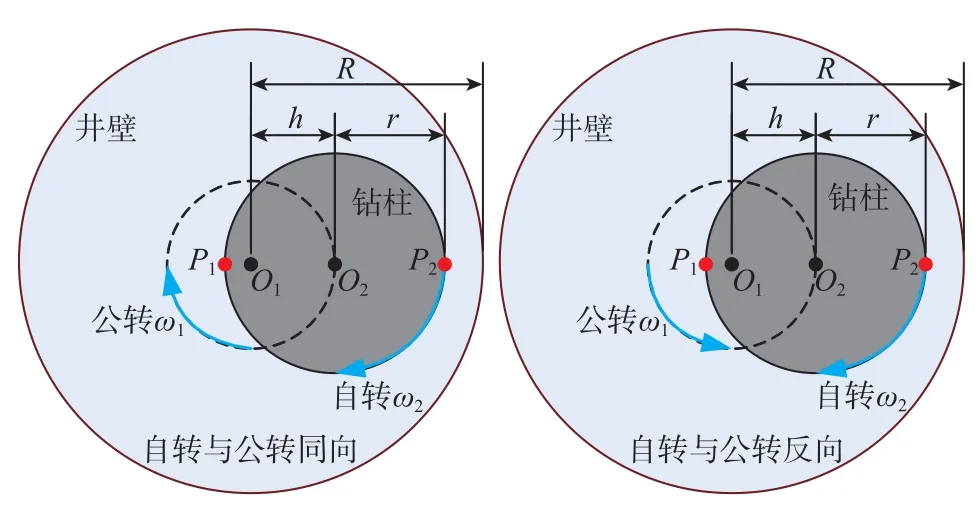
图2　钻柱涡动原理图Fig.2 Principles of drill pipe vortex

设定环空钻井液密度为1.0 g/cm3，轴向流速为2.0 m/s，公转速度为18.84 rad/s，自转速度为18.84 rad/s，考查偏心度分别为0.32、0.64、0.95时各流动参数剖面的变化规律。

切向速度剖面：偏心度增大，宽间隙处切向速度剖面变大变宽，窄间隙处的切向速度剖面整体增大，钻柱外壁面在宽间隙处根据式（3）的推导切向速度越小，在窄间隙处根据式（4）的推导切向速度越大，如图3a。合速度剖面：偏心度增大，宽间隙处合速度剖面整体增大，窄间隙处合速度剖面整体减小，钻柱外壁面在宽窄间隙处的变化规律同切向速度的变化规律，如图3b。

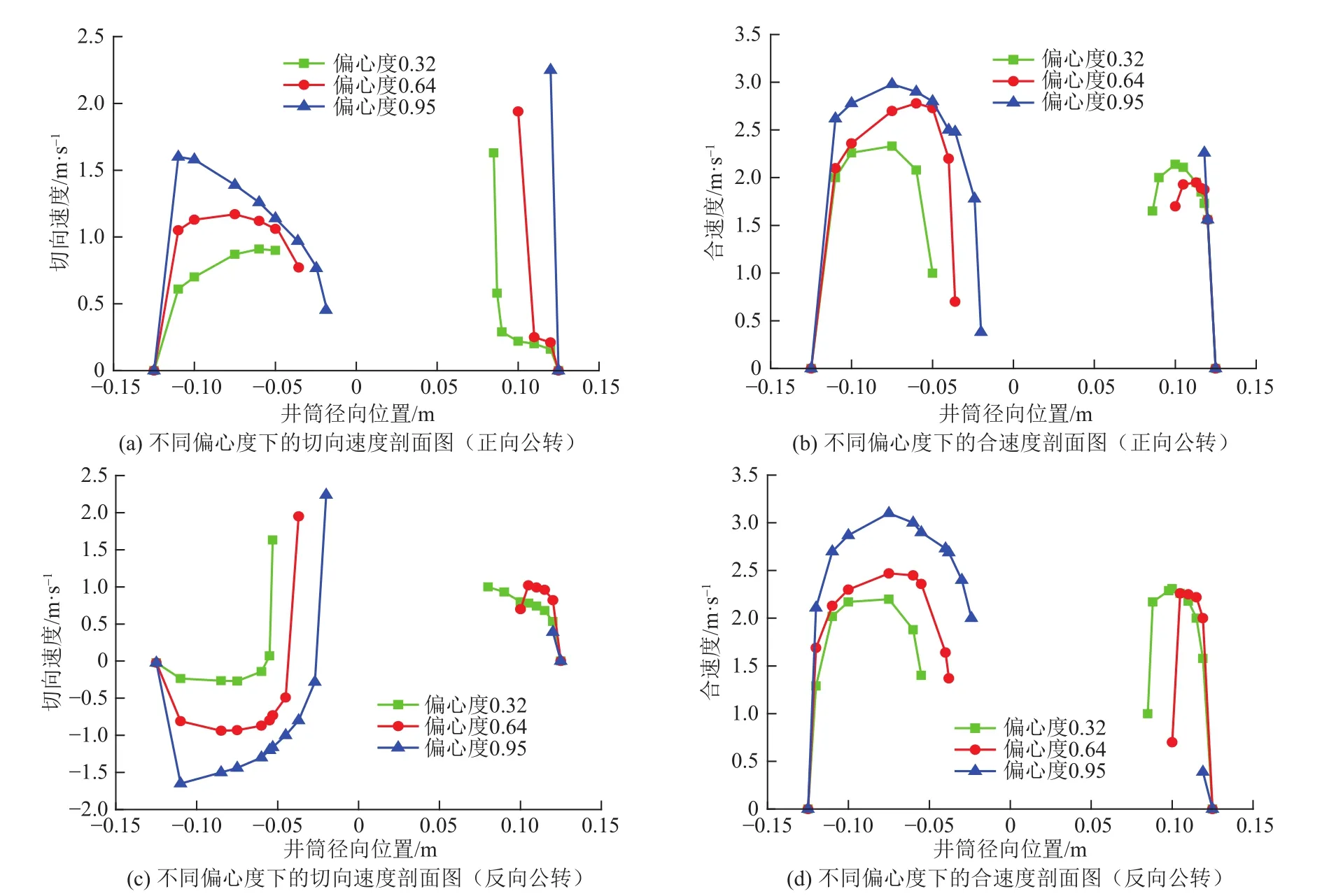
图3　偏心度对流场速度剖面的影响Fig.3 Impacts of eccentricity on flow field velocity profile

设定环空钻井液密度为1 000 kg/m3，轴向流速为2.0 m/s，公转速度为-18.84 rad/s，自转速度为18.84 rad/s，考查偏心度分别为0.32、0.64、0.95时各流动参数剖面的变化规律。

切向速度剖面：随偏心度增大，宽间隙处的切向速度剖面整体反向增大，窄间隙处的切向速度剖面先增大后减小，钻柱外壁面在宽间隙处根据式（5）的推导切向速度正向增大，在窄间隙处根据式（6）的推导切向速度减小，井壁处切向速度为0，如图3c。

合速度剖面：随偏心度增大，宽间隙处合速度剖面整体增大，窄间隙处的合速度剖面整体减小，钻柱外壁面宽窄间隙处的变化规律同切向速度的变化规律，如图3d。

2.2二次流的分析

Analysis for secondary flows

反向公转时，宽间隙钻柱外壁面附近的流体质点跟随钻柱自转呈正向旋转，此处的切向速度为正值，但在远离钻柱外壁面的区域，由于钻柱正向自转的趋势弱于反向公转的趋势，故此区域的流体质点跟随钻柱反向公转，所以此处切向速度为负值，如图3c所示。在宽间隙区域，同时出现正反2个方向的切向速度，两股不同方向的旋流在环空窄间隙的两侧分离与汇合，使得环空宽间隙处出现一个明显的大涡，环空窄间隙处由于钻柱旋转壁面带动的旋流将本应对应出现的另一个不对称的小涡淹没，最终形成了不对称的二次流，如图4所示。

图4　不同偏心度下的截面二次流矢量图（ρ=1 000 kg/m3，v=2.0 m/s，ω1=-18.84 rad/s，ω2=18.84 rad/s）Fig.4 Vector diagram for secondary flows under different eccentricities（ρ=1 000 kg/m3，v=2.0 m/s，ω1=-18.84 rad/s，ω2=18.84 rad/s）

反向公转时，其他参数不变，偏心度越大，越不容易出现二次流。宽间隙处二次流产生的大涡越靠近旋转钻柱外壁面，同时二次流的分离与汇合点越靠近窄间隙处，当偏心度大到一定程度后，钻柱的正向自转趋势被二次流在宽窄间隙处的反向流动趋势完全包裹且基本抵消掉，此时状态与偏心环空自转的螺旋流场（自转方向为反向，自转速度大小同公转）最为接近。二次流的明显出现使得环空流体质点的脉动趋势进一步加强，随着偏心度减小，钻柱正向自转趋势越不容易被抵消，二次流趋势越明显，偏心环空流动的摩阻压耗将进一步增大。

3 结论Conclusions

（1）偏心度对涡动流场的影响较为复杂，不能轻易忽略。宏观上不论公转方向如何，随偏心度增大，宽间隙处的合速度剖面整体增大，窄间隙处的合速度剖面整体减小，但当具体分析不同公转方向的环空流场时，又有各自截然不同的流动特性。

（2）正向公转时，钻柱的自转和公转共同增强了宽窄间隙处的正向旋流趋势，此时切向速度整体为正值，无二次流出现，偏心度增大，宽间隙处切向速度增大。

（3）反向公转时，切向速度同时出现正反向旋流趋势，钻柱的公转流场与自转流场出现相互抵消状态，环空截面呈现不对称的二次流。偏心度减小，宽间隙处切向速度反向越小，公转流场与自转流场相互抵消越小，二次流趋势越明显，摩阻压耗越大。

References：

［1］魏淑惠. 基于计算流体动力学的偏心环空流场数值模拟［J］.大庆石油学院学报，2007，31（6）：62-64.

WEI Shuhui. CFD numerical simulation of eccentric annuli flow field.［D］. Daqing： Dqing Petroleum Institute， 2007， 31（6）： 62-64.

［2］王常斌，陈皖，田迪，贾雪松，赵海燕.幂律流体偏心环空流场CFD模拟［J］. 钻井液与完井液，2009，26（3）：62-64.

WANG Changbin， CHEN Wan， TIAN Di， JIA Xuesong，ZHAO Haiyan. A CFD simulation of the flow field of a power law fluid in an eccentric annulus［J］. Drilling Fluid & Completion Fluid， 2009， 26（3）： 62-64.

［3］陈皖. 偏心环空流场的数值模拟［D］. 大庆： 大庆石油学院，2009：62-64.

CHEN Wan. Numerical simulation of flow field in eccentric annulus［D］. Daqing： Dqing Petroleum Institute， 2009： 62-64.

［4］朱云伟. 赫巴流体环空流动的CFD模拟［D］. 大庆：东北石油大学，2011：50-52.

ZHU Yunwei. CFD simulation of Herschel-Bulkley fluid flow in annulus［D］. Daqing： Northeast Petroleum University， 2011： 50-52.

［5］李子丰，梁尔国.钻柱力学研究现状及进展［J］.石油钻采工艺，2008，30（2）：1-9.

LI Zifeng， LIANG Erguo. Research and development of drill string mechanics［J］. Oil Drilling & Production Technology， 2008， 30（2）： 1-9.

［6］陈庭根，管志川，刘希圣.钻井工程理论与技术［M］.东营：石油大学出版社，2000.

CHEN Tinggen， GUAN Zhichuan， LIU Xisheng. Drilling engineering theory and technology［M］. Dongying：University of Petroleum Press， 2000.

［7］高德利.钻井科技发展的历史回顾现状分析与建议［J］.石油科技论坛，2004，23（2）：29-39.

GAO Deli. Analysis and suggestion on the history of the development of drilling technology［J］. Petroleum Science and Technology Forum， 2004， 23（2）： 29-39.

［8］高德利.油气井管柱力学与工程［M］.东营：中国石油大学出版社，2006.

GAO Deli. Down-hole tubular mechanics and its applications［M］. Dongying： University of Petroleum Press， 2006.

［9］章扬烈.钻柱运动学与动力学［M］.北京：石油工业出版社，2001.

ZHANG Yanglie. Drillstring kinematics and dynamics ［M］. Beijing： Petroleum Industry Press， 2001.

［10］狄勤丰，王文昌，胡以宝，张小柯.钻柱动力学研究及应用进展［J］.天然气工业，2006，26（4）：57-59.

DI Qinfeng， WANG Wenchang， HU Yibao， ZHANG Xiaoke. Study and application of Drilling string dynamics［J］. Natural Gas Industry， 2006， 26（4）： 57-59.

［11］《中国石油钻井》编辑委员会.中国石油钻井（综合卷）［M］.北京：石油工业出版社，2007.

CHINA PETROLEUM DRILLING editorial board. China petroleum drilling（comprehensive volume） ［M］. Beijing： Petroleum Industry Press， 2007.

［12］李子丰，王兆运，阳鑫军，田新民.钻柱涡动分析及防涡稳定器设计［J］. 石油钻采工艺，2008，30（3）：124-127.

LI Zifeng， WANG Zhaoyun， YANG Xinjun， TIAN Xinmin. Swirling analysis of drilling strings and antiwhirl stabilizers design［J］. Oil Drilling & Production Technology， 2008， 30（3）： 124-127.

［13］REHM B， SCHUBERT J， HAGHSHENAS A，PAKNEJAD A S. Managed pressure drilling［M］. Houston： Gulf Publishing Company， 2008.

［14］KOK M V. TERCAN E. Managed pressure drilling techniques， equipments， and applications［J］. Energy Sources Part A-Recovery Utilization and Environmental Effects. 2012， 34： 591.

［15］GODHAVN J M. Control requirements for automatic managed pressure drilling system［J］.SPE Drilling & Completion. 2010，25（3）： 336-338.

［16］ZHOU J， STAMNES O N， AAMO O M， KAASA G O. Switched control for pressure regulation and kick attenuation in a managed pressure drilling system［J］. IEEE Transactions on Control Systems Technology. 2011，19（2）： 337-379.

［17］HERSCHEL W H， BULKLEY R. Measurement of consistency as applied to rubber-benzene solutions：29th Annual Meeting of the American Society Testing Materials Atlantic City， June 1926 ［C］. Proc. ASTM，26 （II） ： 621-633.

［18］胡茂炎，尹文斌，郑秀华，夏柏如.钻井液流变参数计算方法的分析及流变模式的优选［J］.探矿工程：岩土钻掘工程，2004，（7）：41-45.

HU Maoyan， YIN Wenbin， ZHENG Xiuhua， XIA Boru. Analyses on calculation methods of rheological parameters of drilling fluid and optimization of rheological model［J］. Exploration Engineering：Drilling & Tunneling，2004，（7）： 41-45.

［19］韩洪升，魏兆胜，崔海青，李昌连.石油工程非牛顿流体力学［M］.哈尔滨：哈尔滨工业大学出版社，1993：116-145.

HAN Hongsheng， WEI Zhaosheng， CUI Haiqing， LI Changlian. Non-newtonian fluid mechanics in petroleum engineering［M］. Haerbin： Harbin Institute of Technology Press， 1993： 116-145.

［20］张晋凯，李根生，黄中伟，田守嶒，宋先知.连续油管螺旋段摩阻压耗数值模拟［J］.中国石油大学学报：自然科学版2012，36（2）：115-119.

ZHANG Jinkai， LI Gensheng， HUANG Zhongwei，TIAN Shouceng， SONG Xianzhi. Numerical simulation on friction pressure loss in helical coiled tubing［J］. Journal of China University of Petroleum： Edition of Natural Science， 2012， 36（2）： 115-119.

［21］高学平.高等流体力学［M］.天津：天津大学出版社，2005：16-28.

GAO Xueping. Advanced fluid mechanics［M］. Tianjin： Tianjin University Press， 2005： 16-28.

［22］王福军.计算流体动力学分析——CFD 软件原理与应用［M］.北京：清华大学出版社，2004：122-126.

WANG Fujun. Computational fluid dynamics analysis-Software principles and applications of CFD［M］. Beijing： Tsinghua University Press， 2004： 122-126.

（修改稿收到日期 2016-01-28）

〔编辑 薛改珍〕

Features of vortex flow fields in annuluses with different eccentricities

ZHANG Jinkai1，2， LI Gensheng1， HUANG Zhongwei1， TIAN Shouceng1， SONG Xianzhi1， WANG Haizhu1
1. State Key Laboratory of Petroleum Resources and Prospecting， Beijing 102249， China；2. SINOPEC Research Institute of Petroleum Engineering， Beijing 100101， China

To further understand features of flow field during vortex in annulus， impacts of eccentricity variations on tangential velocity profile and resultant velocity profile of annulus under different rotation directions were determined according to the fluid dynamics theories and with continuity equation and N-S equation as controlling equations. In this study， systematic numerical simulations were performed on flows of Hershel-Bulkley fluid in annulus during vortex of drill pipes by using fluid dynamics. Through comparison of simulation data， it is seen that distributions of flow fields in the annulus are significantly different in different rotation directions. During rotation in positive direction， tangential velocity increases with the increases of revolution speed， speed of autorotation and eccentricity around wide clearance of annulus. During rotation in negative position， secondary flows are observed， and tangential velocity decreases reversely with the decreases of eccentricity in wide clearance of the annulus. Moreover， more obvious the trends of secondary flows， higher the frictional pressure losses. Proper application of these patterns may improve existing hydraulic theories for drilling operations to highlight properties of flow fields in the annulus and to provide theoretical guidance for design and optimization of hydraulic parameters for drilling operations.

vortex； annulus； Hershel-Bulkley fluid； frictional pressure loss； numerical simulation； flow field

ZHANG Jinkai， LI Gensheng， HUANG Zhongwei， TIAN Shouceng， SONG Xianzhi， WANG Haizhu. Features of vortex flow fields in annuluses with different eccentricities［J］.Oil Drilling & Production Technology， 2016， 38（2）： 133-137.

TE21

A

1000 -7393（ 2016 ） 02 -0133-05

10.13639/j.odpt.2016.02.001

国家重点基础研究发展计划（973计划）“深井复杂地层安全高效钻井基础研究”（编号：2010CB226704）。

张晋凯（1980-），2013年毕业于中国石油大学（北京）油气井工程专业，现从事油气井流体力学与工程方面的研究。通讯地址：（100101）北京市朝阳区北辰东路8号北辰时代大厦10层。E-mail：bob33@163.com

李根生（1961-），中国工程院院士，教授，博士生导师，从事油气钻井和完井工程方面的研究和教学。通讯地址：（102249）北京市昌平区府学路18号中国石油大学（北京）石油工程学院。电话：010-89733935。E-mail：ligs@cup.edu.cn

引用格式：张晋凯，李根生，黄中伟，田守嶒，宋先知，王海柱.不同偏心度的环空涡动流场特性［J］.石油钻采工艺，2016，38（2）：133-137.