基于智能算法的铅带轧制过程负荷分配系数优化

蒋澄灿　芮延年　廖黎莉　管　淼　沈　铭

苏州大学, 苏州,215021



基于智能算法的铅带轧制过程负荷分配系数优化

蒋澄灿芮延年廖黎莉管淼沈铭

苏州大学, 苏州,215021

摘要：针对铅带连轧过程负荷分配优化问题，以均衡分配为目标，通过对遗传算法和变尺度(BFGS)混合优化算法的研究，提出了基于变尺度混合遗传算法(MSHGA)的铅带轧制过程负荷分配系数优化计算方法。通过仿真实验对算法的可行性进行了验证。结果表明，在保证铅带轧制板形、厚度、精度和性能指标参数不变的情况下，优化后的总轧制力较经验负荷算法的相应结果减小了10.7%。该技术方法的研究为铅带轧制节约电能提供了参考。

关键词：铅带连轧；智能算法；负荷分配优化；混合优化算法

0引言

高速宽铅带多辊连轧机(简称铅带连轧机)中轧制辊的负荷分配十分重要。合理的负荷分配策略可以有效降低能耗、提高轧制速度，保证产品质量。

负荷分配方法主要有经验法和能耗曲线法等。经验法是根据生产者的经验将轧制参数以数据库表格形式存储于计算机中，这种方法简便易行，但是过于依赖操作者的经验，轧制的板带厚度不易及时调整，容易导致各机架负荷不均[1]。能耗曲线法是从大量的生产数据中整理能耗与各机架轧制厚度之间的数量关系，绘制出单位能耗曲线，用来指导生产，能够克服各机架负荷不均匀现象。不足之处在于绘制能耗曲线需要大量的现场实测数据，针对性强，不适用多品种、多配方、小批量的铅带轧制生产[1]。

由于铅带连轧过程具有多变量、强耦合、非线性、多约束、强时变性等特征，故传统优化方法如Powell法、单纯形加速法等方法在实际生产应用中，存在着迭代过程计算量大、收敛速度慢等问题。

通过前期研究，本文结合遗传算法收敛性好、计算精度要求低、计算时间短、鲁棒性好的优点和变尺度算法适用于高维数计算的优点，提出基于变尺度混合遗传智能算法的铅带轧制过程负荷分配系数优化算法。受江苏三环实业有限公司的委托，以其研发的铅带连轧机为研究模型，开展研究工作。

1连轧数学模型

1.1经验负荷分配(厚度分配)模型

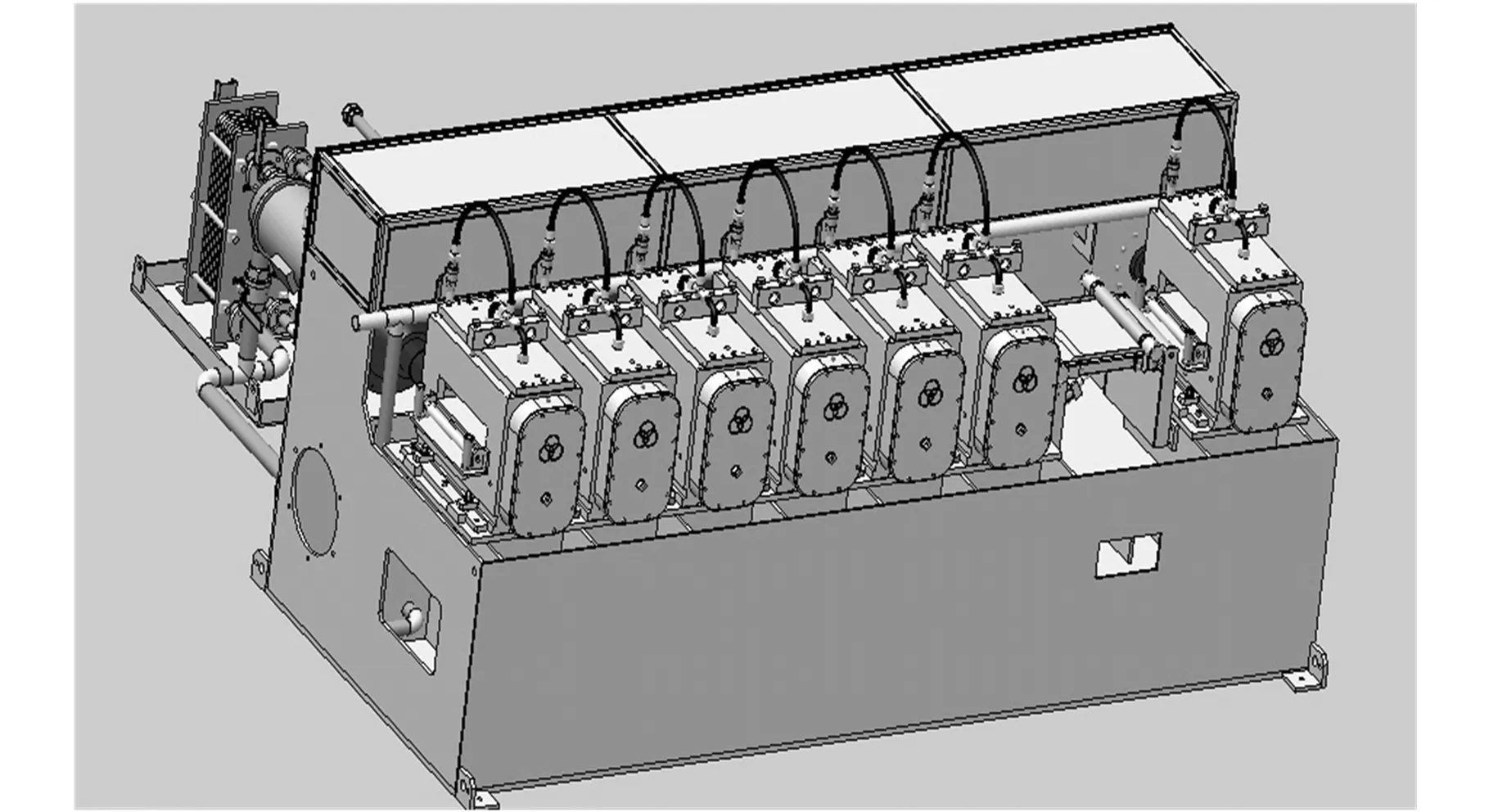
图1　铅带连轧机模型

铅带连轧机的模型如图1所示。铅带通过连轧机组，在各架轧机轧制力的作用下，将厚度为H的铅带轧制成厚度为hn的成品，其总压下量为

Δh=H-hn

(1)

根据实际生产数据，结合单位能耗和轧出厚度，经过统计计算，绘出一种以单位质量轧件消耗的能量为变量，轧件延伸率为自变量的能耗曲线。为了便于计算及应用，将此能耗曲线转换成负荷分配经验公式，公式为[2]

(2)

(3)

式中，B1、B2为累计轧制力的能耗系数；Pn为n个机架的总轧制力；βi为第i个机架的负荷分配比；hi为第i个机架出口铅带厚度(i=1，2，…，7)，mm。

1.2轧制力模型

目前最适用于铅带连轧机组轧制力模型的理论公式是基于OROWAN变形区力平衡理论的SIMS公式，其轧制力模型为[2]

(4)

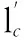
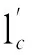
(5)

(6)

Δhi=hi-1-hi

(7)

式中，R′为压扁后轧辊半径，mm；R为轧辊半径，mm；Δhi为绝对压下量，mm；hi-1为第i个机架入口铅带厚度，mm。

外摩擦应力状态系数QP采用Hill公式计算：

(8)

(9)

(10)

式中，μ为接触弧摩擦因数；ε为压下率；α为润滑剂的种类与质量影响系数；v为轧件出口速度，m/s。

2目标函数

连轧机组的轧制过程分成三个阶段：第一个机架考虑到坯料的波动以及咬入的困难，可适当减小压下量，以保证连轧机组的顺利进行；第二、第三个机架轧制目标侧重于尽量充分发挥设备的能力，给予尽可能大的压下量，根据经验一般要求，第一个机架的轧制力F1尽量接近第二个机架的轧制力F2的0.9倍，即F1/F2=K1≈0.9，第二、第三个机架轧制力大约相等，即F2/F3=K2≈1；从第三个机架开始，轧制目标侧重于板形、厚度精度，轧制力应逐架递减。基于以上因素，将轧制过程的模型分为三个部分[3]。

第一阶段(机架1～2)：此阶段的目标是负荷分配是否均衡，第一个机架适当保留机架的轧制能力，第二个机架则充分发挥轧制能力，以最大的压下量轧制，以达到高产的目的。此阶段目标函数为

J1=min((F1-K1F2)2)

(11)

第二阶段(机架2～3)：此阶段的目标依然是负荷分配是否均衡，为了充分利用设备能力，第二、第三个机架应尽量保持轧制力相等，该阶段以等压力分配作为优化的目标函数,即

J2=min((F2-K2F3)2)

(12)

第三阶段(机架4～7)：此阶段产品已接近成形，轧制目标应为板形最优，以保证生产质量，各机架轧制力依次递减，此阶段目标函数为

(13)

式中，Ci/hi为(机架4～7)的相对凸度；Cn/hn为相对应成品铅带的相对凸度。

综上所述可以看出，连轧机组的7个机架工艺条件各不相同，机架轧制速度呈非线性变化。其最优的综合目标函数为

J=J1+J2+J3=

(14)

3约束条件

根据铅带冷连轧机组的特点，设定限制条件如下[4-6]：

(1)设备强度能力的限制。施加在各机架上的轧制力应小于其最大允许值。

(2) 板形限制。为了保持良好板形，除了正确设计辊形外，应合理安排后机架的压下量，使其相应的轧制力之间有一定的比例，即

(15)

4混合算法

遗传算法是一种基于生物自然选择的算法。它具有收敛性好、计算精度要求低、计算时间短、鲁棒性好等优点。理论和实践已经证明遗传算法容易产生早熟和局部寻优能力较差等问题。利用变尺度算法适用于高维数计算的优点，并与铅带连轧结合起来，构成了基于变尺度混合遗传智能算法的铅带轧制过程负荷分配系数优化算法。

对于铅带连轧机组，传统模式负荷分配要求各机架的轧制力满足如下关系式[7]：

(16)

式中，Fi为第i机架轧制力；αi为第i机架目标负荷分配系数；n为铅带连轧机组机架数目(n=7)。

式(16)可写成另外一种形式的非线性方程组：

(17)

将方程组式(17)写成向量形式后作Taylor展开，展开后得到矩阵方程[8-9]：

(18)

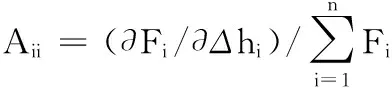
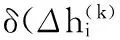
变尺度混合遗传算法计算流程如图2所示[10-13]。

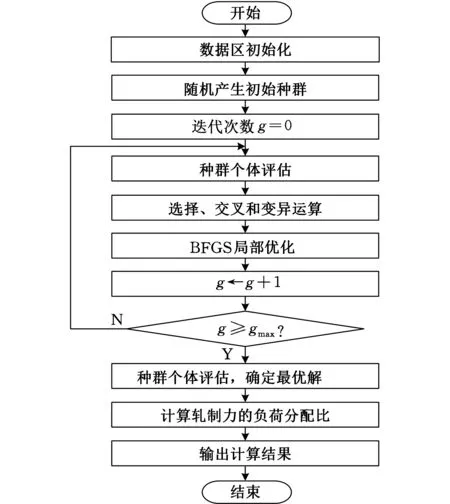
图2　变尺度混合遗传算法计算流程

5仿真试验

本文选取课题组与江苏三环有限公司共同开发的铅带连轧机为研究对象，来料宽度B=315 mm，来料厚度H=8 mm，成品厚度h=1 mm，机架数为7。本文所涉及的铅带连轧机组的一些主要设备机械及工艺参数见表1。试验中分别得出经验负荷分配值和变尺度混合遗传算法优化后的负荷分配值，试验结果如表2、表3所示。

结合表2和表3，分别给出出口厚度、压下率和轧制力三种分配方式的对比曲线，如图3～图5所示。

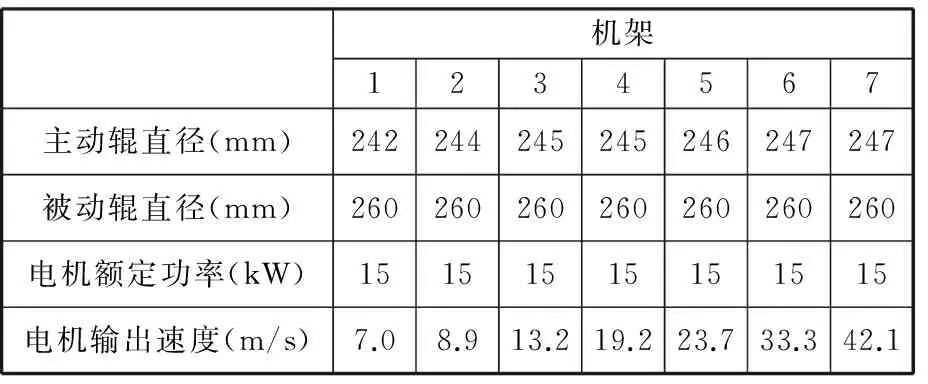
表1　铅带连轧机组主要工艺参数

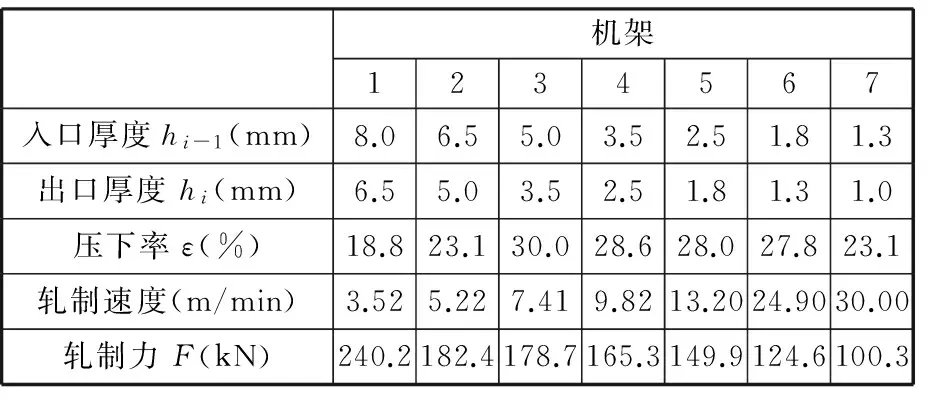
表2　各机架经验负荷分配结果

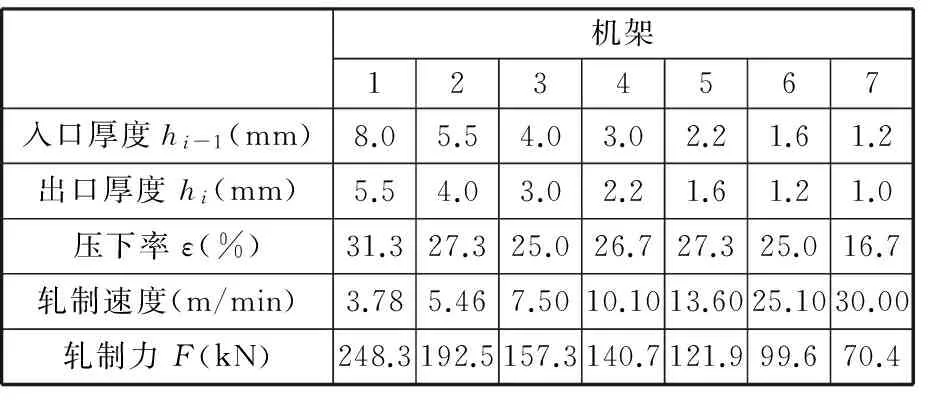
表3　变尺度混合遗传算法优化后各机架负荷分配结果

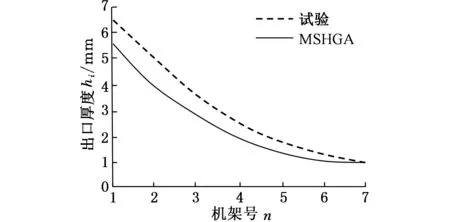
图3　各机机架号架出口厚度对比图

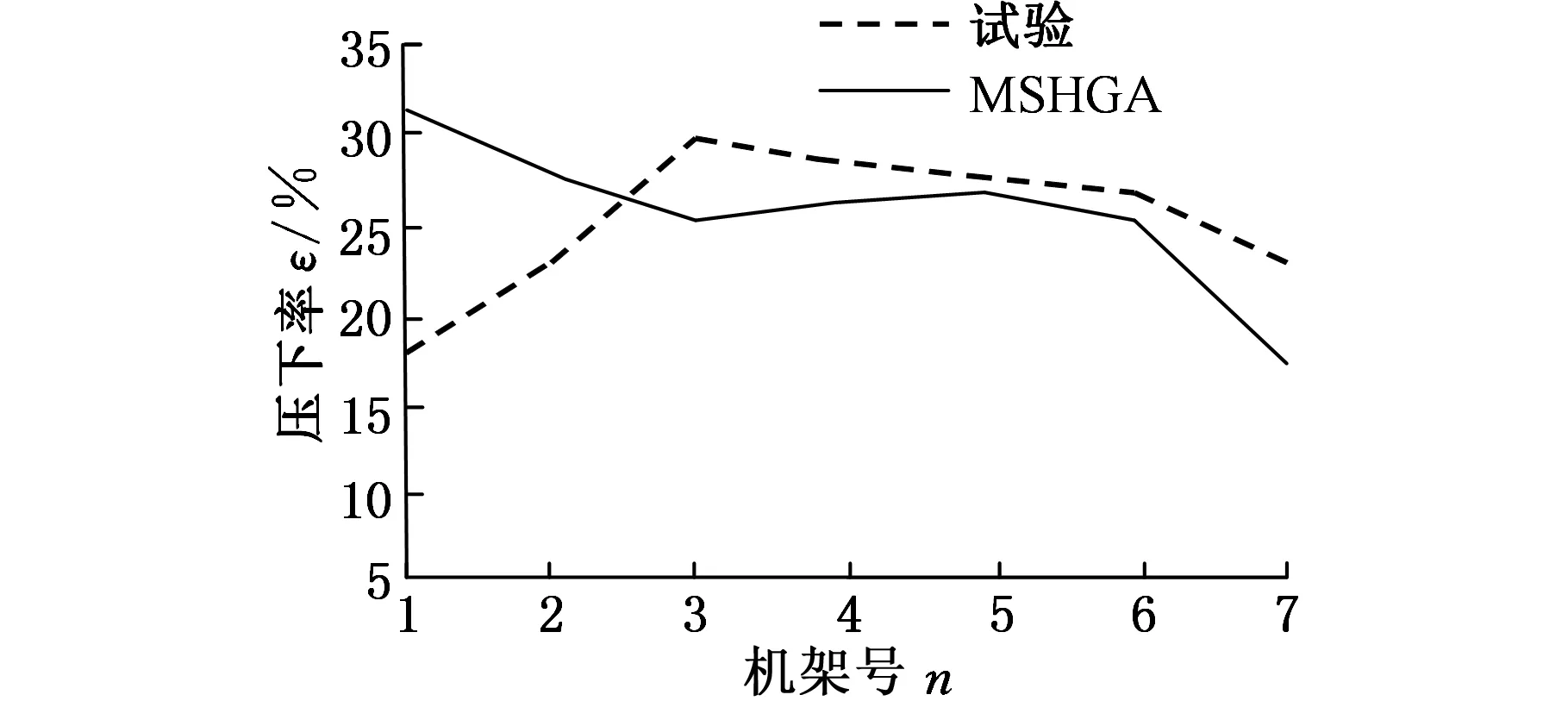
图4　各机架压下率对比图

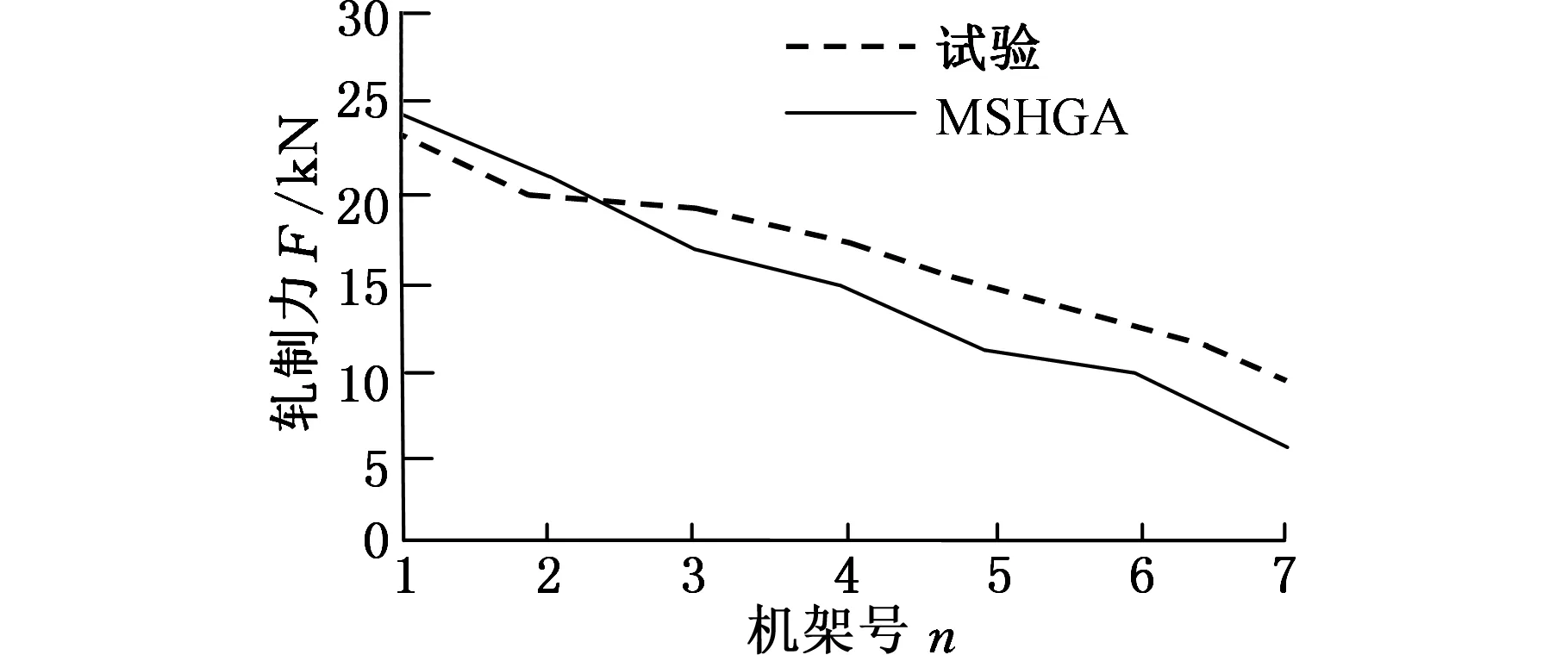
图5　各机架轧制力对比图

从图3～图5可以看出，采用MSHGA优化方法之后，上游机架充分利用铅带的高温特性，尽可能实现了最大压下量，下游机架轧制力逐渐减小，这有利于保证铅带板形、厚度精度和性能指标的要求。根据经验负荷分配的总轧制力为1141.4 kN；而采用本文所构建的基于变尺度混合遗传智能算法的铅带轧制过程负荷分配系数优化算法，总轧制力为1030.7 kN。相比之下，在保证轧制需要的前提下，总轧制力减小了10.7%。

综合以上分析，经验负荷分配的轧制力分布没有达到负荷均衡最优的目标，但是经过MSHGA优化后的负荷分配，很好地完成了对经验负荷分配的优化，轧制力分配更加合理，同时又保证了铅带轧制过程的最优，取得了很好的效果。

参考文献：

[1]姜万录,张生. 改进的量子遗传算法在冷连轧机负荷分配中的应用研究[J]. 燕山大学学报,2013，37(1):8-14.JiangWanlu,ZhangSheng.ApplicationResearchonImporvedQuantumGeneticAlgorithmforLoadDistributionOptimizationofTandemColdRollingMill[J].JournalofYanshanUniversity, 2013，37(1):8-14.

[2]孙一康. 冷热轧板带轧机的模型与控制[M]. 北京:冶金工业出版社,2010.

[3]万馨. 基于智能算法的带钢轧制过程负荷分配技术的研究[D]. 苏州:苏州大学,2014.

[4]NezhadAM,ShandizRA,JahromiAE.AParticleSwarm-BFGSAlgorithmforNonlinearProgrammingProblems[J].Computers&OperationsResearch, 2013，40(4):963-972.

[5]LiuHui,TianHongqi,LiangXifeng,etal.NewWindSpeedForecastingApproachesUsingFastEnsembleEmpiricalModelDecomposition,GeneticAlgorithm,MindEvolutionaryAlgorithmandArtificialNeuralNetworks[J].RenewableEnergy, 2015，83:1066-1075.

[6]AltinkayaH,OrakM,EsenI.ArtificialNeuralNetworkApplicationforModelingtheRailRollingProcess[J].ExpertSystemswithApplications, 2014，41(16):7135-7146.

[7]李维刚, 张健明. 带钢热连轧轧制力模式负荷分配的改进算法[J]. 宝钢技术,2012(4):6-10.LiWeigang,ZhangJianming.ImprovedAlgorithmforLoadDistributionintheRollingForceModeforHotStripMills[J].BaosteelTechnology, 2012(4):6-10.

[8]张进之,吴增强. 热连轧生产过程负荷分配分析[J]. 世界钢铁,2013，13(1):48-53.

ZhangJinzhi,WuZengqiang.AnalysisontheLoadDistributionofHotRollingMill[J].WorldIron&Stell, 2013，13(1):48-53.

[9]李维刚,刘相华. 热连轧机轧制力成比例负荷分配的CLAD算法[J]. 东北大学学报(自然科学版),2012，23(3):352-356.

LiWeigang,LiuXianghua.CLADAlgorithmofRollingRatioLoadDistributiononHotStripMill[J].JournalofNortheasternUniversity(NaturalScience), 2012，23(3):352-356.

[10]PoursinaM,DehkordiNT,FattahiA,etal.ApplicationofGeneticAlgorithmstoOptimizationofRollingSchedulesBasedonDamageMechanics[J].SimulationModellingPracticeandTheory, 2012,22(3):61-73.

[11]WangPengfei,PengYan,LiuHongmin,etal.ActuatorEfficiencyAdaptiveFlatnessControlModelandItsApplicationin1250mmReversibleColdStripMill[J].JournalofIronandSteelResearch,International, 2013,20(6):13-20.

[12]HirtG,SengeS.SelectedProcessesandModelingTechniquesforRolledProducts[J].ProcediaEngineering, 2014,81:18-27.

[13]PericaroGA,SantosSR,RibeiroAA,etal.HLRF-BFGSOptimizationAlgorithmforStructuralReliability[J].AppliedMathematicalModelling, 2015,39(7):2025-2035.

(编辑袁兴玲)

收稿日期：2015-08-24

基金项目：国家高技术研究发展计划(863计划)资助项目(2012AA063506)；苏州市科技支撑项目(ss201344)

中图分类号：TG249.7；TF812

DOI：10.3969/j.issn.1004-132X.2016.12.021

作者简介：蒋澄灿，男，1988年生。苏州大学机电学院博士研究生。主要研究方向为先进制造技术、绿色蓄电池装备技术、机电一体化产品创新技术。芮延年，男，1951年生。苏州大学机电学院教授、博士研究生导师。廖黎莉，女，1981年生。苏州大学机电学院博士研究生。管淼，男，1979年生。苏州大学机电学院博士研究生。沈铭，男，1981年生。苏州大学机电学院博士研究生。

OptimizationofLoadDistributionforLeadwithRollingProcessesBasedonIntelligentAlgorithm

JiangChengcanRuiYannianLiaoLiliGuanMiaoShenMing

SoochowUniversity,Suzhou,Jiangsu,215021

Abstract:Aiming at equilibrium and based on genetic algorithm and BFGS algorithm, the new optimization method was called mutative scale hybrid genetic algorithm(MSHGA), which was used for load distribution of lead with rolling processes and was verified the feasibility through the simulation experiments. The experimental results show that the optimized total rolling force is down 10.7% from empirical load algorithm under the conditions of invariable parameters in rolling strip shape of lead, thickness, precision and performance indicators. The research lays a theoretical basis on save power of lead with rolling.

Key words:lead with rolling; intelligent algorithm; optimization of load distribution; hybrid optimization algorithm