带落角约束的自适应滑模变结构导引律*
张宽桥,杨锁昌,陈鹏,王刚
(军械工程学院 导弹工程系,河北 石家庄 050003)
带落角约束的自适应滑模变结构导引律*
张宽桥,杨锁昌,陈鹏,王刚
(军械工程学院 导弹工程系,河北 石家庄050003)
摘要:针对某些制导武器在精确命中目标的同时还要满足落角约束的要求,基于滑模变结构理论,提出一种带落角约束的自适应滑模变结构导引律。考虑末端弹目视线角速率变化剧烈和变结构抖振现象的问题,选取相对速度偏角作为滑模面,引入落角约束项;将目标机动视为有界干扰,利用Lyapunov理论进行了稳定性分析;采用变开关系数法和饱和函数法相结合的方法,大大削弱了变结构的抖振现象。最后,将该导引律应用于导弹实际模型中进行对比仿真,结果表明所提导引律针对固定目标和机动目标,相比传统方法,都能以更小的脱靶量和落角误差命中目标。
关键词:导引律;落角约束;滑模变结构;相对速度偏角;有限时间收敛;自适应趋近律
0引言
在现代战争中,如何提高制导武器的命中精度和毁伤效能,一直是许多国内外学者研究的热点问题。对于很多制导武器而言,如反坦克导弹、反舰导弹等, 不仅希望能够以较高的精度准确命中目标,还希望能以一定的落角击中目标,以大大增加战斗部的毁伤效能。因此,在设计导引律时,落角约束就成了必须考虑的问题[1]。
鉴于滑模变结构控制对于参数摄动和外界干扰具有很强的自适应性和鲁棒性,再加上其控制算法较为简单,很多文献基于变结构控制理论,通过将终端角度约束条件纳入滑动模态从而推导出具有落角约束的变结构导引律[2-8]。文献[2]在比例导引方法的基础上,基于变结构控制理论提出了一种带落角约束的变结构导引律,并对机动目标具有很好的鲁棒性;文献[3]针对机动目标,在球坐标系下构建了弹目三维相对运动模型,基于滑模控制理论,设计了一种能够实现垂直击中机动目标,且对目标机动加速度的变化有很强的鲁棒性和适应能力的带攻击角度约束的三维制导律;文献[4]在考虑落角约束的同时,还加入了对攻击时间的约束,但是这两种变结构导引律形式都过于复杂;文献[6]将滑模控制方法用于解决导弹对目标拦截时的攻击角度约束问题,并采用饱和函数法代替符号函数,用以削弱滑模面抖振现象;文献[8]针对无动力再入飞行器的末制导问题,提出了以滑模控制理论为基础的导引律,保证命中精度的同时满足落角要求。上述这些文献基本都以弹目视线角速率或弹目相对距离与视线角速率的乘积作为滑模面,同时引入终端角度约束,但视线角速率随弹目相对距离的减小会剧烈变化,使得制导武器在末端姿态变化较大,稳定性较差。针对这个问题,文献[9-10]选取相对速度偏角作为滑模面,设计了基于零化相对速度偏角的变结构末制导律,但是没有对落角约束、抖振削弱问题和有限时间收敛特性进行分析和研究。
本文在文献[10]的基础上,基于变结构理论,设计了针对固定目标和机动目标的带落角约束的自适应滑模变结构导引律,并对其制导性能进行了分析。导引律选取相对速度偏角和落角约束项作为滑模面,采用自适应指数趋近律,能够自适应的调节趋向滑模面的速率,将目标运动信息视为有界干扰;运用Lyapunov稳定性理论对其稳定性进行了分析,同时对滑模面有限时间可达性进行了证明;综合采用变开关系数法和饱和函数法对其抖振现象进行了抑制。最后,将该引入到导弹的实际模型中进行对比仿真分析,结果表明,所提导引律能够很好满足制导精度和落角约束的要求,能以更小的脱靶量和落角误差精确命中目标,验证了所提导引律的有效性和优越性,且所设计导引律形式简单,易于工程实现。
1弹目相对运动模型
在进行导引律设计前,首先以纵向平面为例,建立弹目相对运动模型,如图1所示。在建模过程中,作出如下假设:
(1) 导弹和目标视为质点;
(2) 导弹和目标的加速度矢量方向与速度矢量方向垂直,即施加在导弹和目标上的加速度只改变速度的方向,不改变速度的大小。
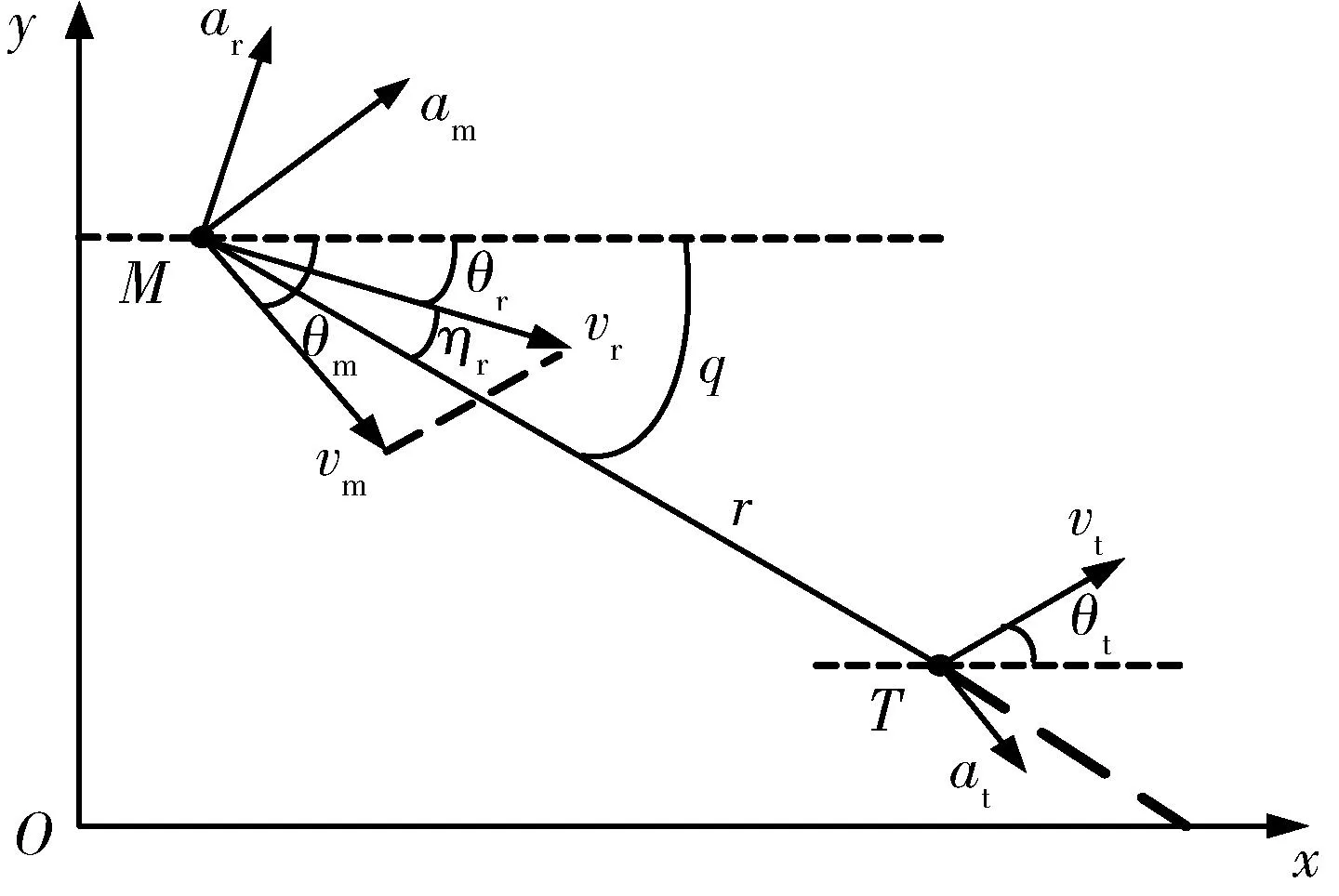
图1 纵向平面内弹目相对运动模型Fig.1 Missile to target motion model in longitudinal plane
在图1中,M表示导弹,T表示目标,vm为导弹速度,θm为导弹弹道倾角,am为导弹加速度,vt为目标速度,θt为目标航迹倾角,at为目标加速度,r为弹目之间相对距离,q为弹目视线角,vr为弹目相对速度,即vr=vm-vt,ar为弹目相对加速度,ηr为弹目相对速度偏角,即弹目相对速度方向与弹目视线之间的夹角。规定所有角度逆时针方向为正,反之为负。
基于上述假设及弹目相对运动关系,可以得出弹目相对运动关系方程组:
(1)
2俯仰通道导引律设计与分析
2.1带落角约束的滑模导引律的推导
从图1可以看出ηr=q-θr,当q=θr时,即ηr=0,能够保证导弹命中目标,并且制导末端ηr不会像q那样随着弹目相对距离的减小而急剧增大,因此选择ηr作为滑模面,不仅能够解决q在制导末端剧烈变化的问题,还能以准平行接近法对目标进行攻击,弹道更平滑,对控制系统的要求相对较低,同时考虑到末端角度约束的问题,因此选取的滑模面切换函数为
s1=ηr+k1(q-qd),
(2)
式中:k1>0;qd为期望落角。切换函数的第1项使弹目相对速度偏角趋近于0,保证导弹能够命中目标,第2项保证终端落角约束要求。
为保证有限时间到达滑模面,可对系统进入滑模动态前的过程(趋近律)进行设计[11]。对于趋近律的选择,常用的主要有等速趋近律、指数趋近律、幂次趋近律等,为保证到达条件和良好的动态性能,以及考虑控制系统的时变性,选取一种对时变参数具有自适应能力的指数趋近律[12],其形式如下:
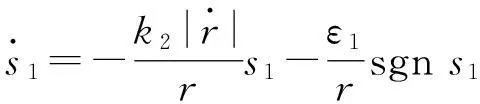
(3)
式中:k2>0,ε1>0。该趋近律的自适应性主要体现在滑模面切换函数向滑模面运动的速率随着r的变化进行自适应调整。在末制导开始阶段,r值较大,趋近速率较慢,产生的制导指令较为适度,能够有效避免制导指令出现饱和,同时减小弹上各部件的负担,不至于产生较大的过载,随着r逐渐减小趋近于零,趋近速率迅速增大,促使s1收敛到0避免发散。正是趋近律函数的自适应性,使得设计的导引律具有了自适应性,并且当s1趋近于零时,趋近速率约为ε1/r,能够保证有限时间到达滑模面。
由图1可得
ar=amcos(q-ηr-θm)-atcos(q-ηr-θt),
(4)
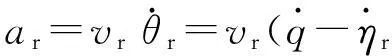
(5)
综合式(4)和式(5)可得:
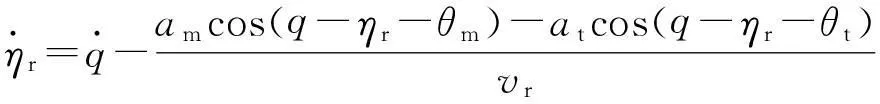
(6)
对式(2)进行微分可得
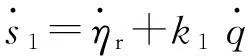
(7)
将式(6)带入式(7),然后结合式(3)可得
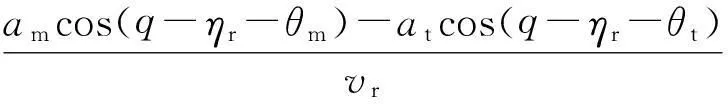
(8)
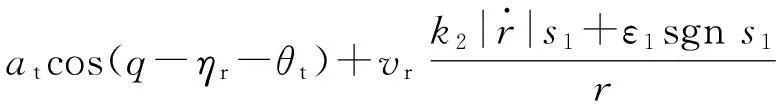
(9)
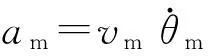
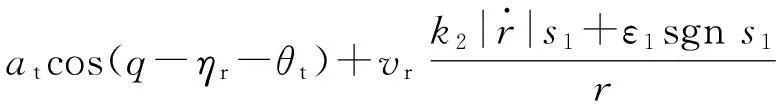
(10)
在导弹实际制导控制过程中,对于目标的运动加速度以及方位信息是很难获得的,通常通过卡尔曼滤波技术进行在线估计,但可能会存在很大的误差,所以式(10)中的atcos(q-ηr-θt)项很难进行计算。在实际交战过程中,目标的速度和机动能力远小于导弹,且目标的机动有一定的范围,假设 |at| ≤M,其中M为目标可能的最大机动加速度值,则有atcos(q-ηr-θt)≤M。基于变结构控制对外界干扰的鲁棒性,可将目标的机动项视为有界干扰,对式(10)进行简化可以得到带落角约束的自适应滑模变结构导引律形式为
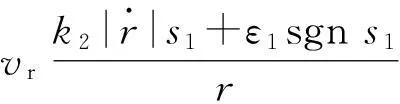
(11)
由图2弹目相对速度关系可以得到:
(12)
从而得到弹目相对速度以及弹目相对速度偏角的表达式:
(13)
2.2非奇异性分析
从式(11)可以看出所设计的导引律中存在三角函数分母项vmcos(q-ηr-θm),需要对其非奇异性进行证明。
由图1知:
vrcosηr=vmcos(q-θm)-vtcos(q-θt),
(14)
vrsinηr=vmsin(q-θm)-vtsin(q-θt).
(15)
将式(14)和式(15)左右两边分别乘以cosηr和sinηr,然后两式相加得
vr=vmcos(q-θm)cosηr+vmsin(q-θm)sinηr-
vtcos(q-θt)cosηr-vtsin(q-θt)sinηr=
vmcos(q-θm-ηr)-vtcos(q-θt-ηr).
(16)
从而可以得到:
vmcos(q-θm-ηr)=vr+vtcos(q-θt-ηr)≥vr-vt.
(17)
在导弹对目标进行攻击的过程中,导弹的速度远大于目标的速度,因此,弹目相对运动速度要大于目标的速度,即vr-vt>0,则由式(17)可得vmcos(q-θm-ηr)>0,从而证明了式(11)所得的导引律方程是非奇异的。
2.3稳定性分析
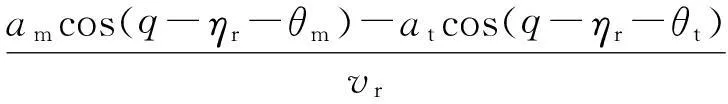
(18)
将式(9)带入式(18)得
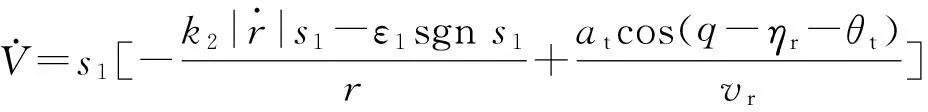
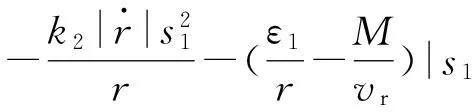
(19)
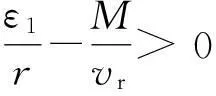
对于制导武器而言,末制导时间是有限的,因此必须保证有限时间内系统状态到达滑模面。所以必须对滑模面有限时间可达性进行证明,保证末制导系统的稳定性。本文基于有限时间稳定性理论[13]对滑模面有限时间可达性进行如下证明:
由式(19)可得
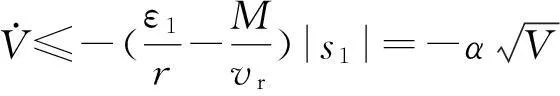
(20)
对式(20)进行积分求解可得
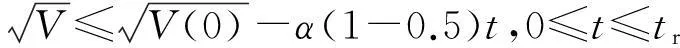
(21)
V=0,t≥tr,
(22)
令V(0) = 0,即可得到系统状态完成趋近过程到达滑模面所用时间为
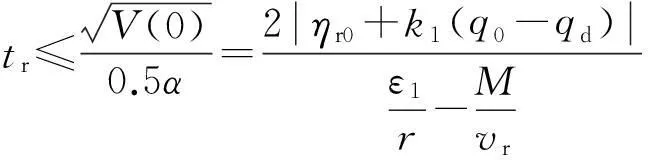
(23)
从式(23)可以看出,到达滑模面所需时间与制导参数成正比关系,与ε1成反比关系,因此通过增大k1减小ε1的值,可以有效减小到达滑模面所需时间,因此可以保证在末制导段内系统到达滑模面。
2.4削弱抖振
虽然变结构控制具有对控制系统的参数摄动和外部干扰的强鲁棒性,但却是以控制量的高频抖振为代价来换取的。抖振现象是变结构控制本身固有的,它不仅会降低系统控制精度,而且还会破坏系统性能,因此,如何大大降低抖振的影响,就成为了提高变结构导引律的关键问题[14]。为削弱抖振,很多学者进行了相应的研究,目前较为常用的方法有饱和函数法、变开关系数法、双曲正切函数法等,本文将变开关系数法和饱和函数法进行结合,并应用于制导律的设计中以削弱抖振。
饱和函数法是将不连续的符号函数进行连续化,将符号函数用式(24)替换:
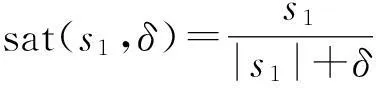
(24)
式中:δ>0,为一较小数,一般称为边界厚度,也称为消颤因子[15]。由式(24)结合导引律形式,可以看出δ与制导控制指令的大小成反比关系,较小的δ能够增强控制效果,但是取值过小会增大抖振。因此需要根据实际情况选取适当的δ值,达到消弱抖振同时不影响控制效果。
变开关系数法主要通过改进ε1的形式,增加其自适应性,从而达到降低抖振的目的。一般的趋近律将ε1设为定值,若取值较小,趋近滑模面的速率较慢,能有效降低抖振,若取值过小,会导致趋近滑模面的时间很长,滑模变结构控制就失去了意义。针对这个问题,本文对ε1的形式进行改进,使其随着r的变化自适应调整,其具体形式如下:
ε1=a1r+b1,
(25)
式中:a1>0,b1>0,其取值与ε1的上下限和r的初值有关。
当r逐渐趋于0时,可由ε1的下限确定b的值,保证制导系统处在滑模控制下;在末制导段,根据r的最大值和ε1的上限,可以确定a1的取值,在保证系统较快的趋近滑模面的同时降低抖振幅值。
利用式(24)代替符号函数,并将式(25)带入式(11)中可得改进后的导引律形式为
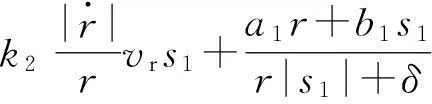
(26)
3偏航通道导引律设计
在水平面内建立弹目相对运动模型,如图2所示。
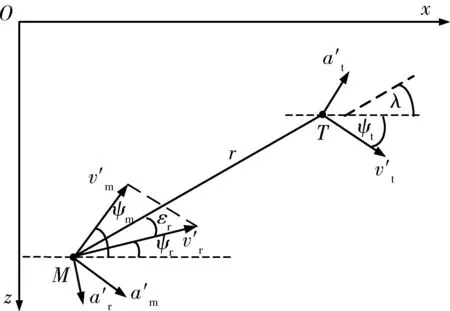
图2 水平面内弹目相对运动模型Fig.2 Missile to target motion model in lateral plane
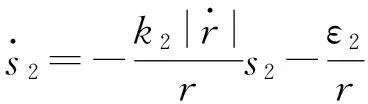
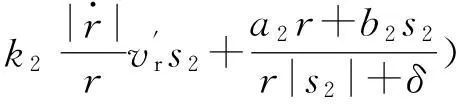
(27)
(28)
4仿真分析
为验证所设计的导引律的有效性和优越性,将所设计的带落角约束的自适应滑模变结构导引律(VSG)引入某型反坦克导弹实际数学模型中进行对比仿真分析。在地面惯性坐标系下,选取发射点为坐标原点,导弹初始位置为xm0=ym0=zm0=0m,初始速度为0,目标初始位置为xt0= 2 000 m,yt0=zt0=0m,当导弹发射后在Ox轴方向运动距离为800 m时,开始进入末制导段,并规定此时刻为仿真零时刻,即t= 0。将本文设计的导引律与带落角约束的比例导引律(BPN)进行对比仿真,比例导引律的表达形式如下:
(29)
式中:θ和ψ分别为弹道倾角和弹道偏角;q和λ分别为纵向平面和水平面内弹目视线角;Kq和Kλ为比例导引系数;qd为期望落角;tgo为剩余飞行时间;Rr和vr为弹目距离和相对速度;Rrx和Rry为x轴和y轴上弹目之间距离。
下面根据目标运动状态以及期望落角不同分为3种场景进行仿真分析。
仿真场景1:目标为固定目标,设定的期望落角为-50°。
仿真结果如表1和图3~5所示。表1为针对固定目标,2种导引律制导性能的仿真结果对比。图3为2种不同制导体制下,导弹和目标在空间中的运动轨迹,由于导弹在末制导段前为程序控制段,因此导弹运动轨迹在前半段重合;由于采用自适应指数趋近律,在末制导初段弹目距离较大,趋近速率较慢,控制指令较为适度,所以末制导初段VSG弹道较高,随着弹目距离减小,滑模面趋近速率增大,控制指令也相应增加,所以末制导段后期VSG和BPN的弹道高度基本一致,验证了VSG算法的自适应性。图4为导弹姿态角的变化曲线,图5为导弹在弹体坐标系下所受过载曲线。

表1 场景1制导仿真结果
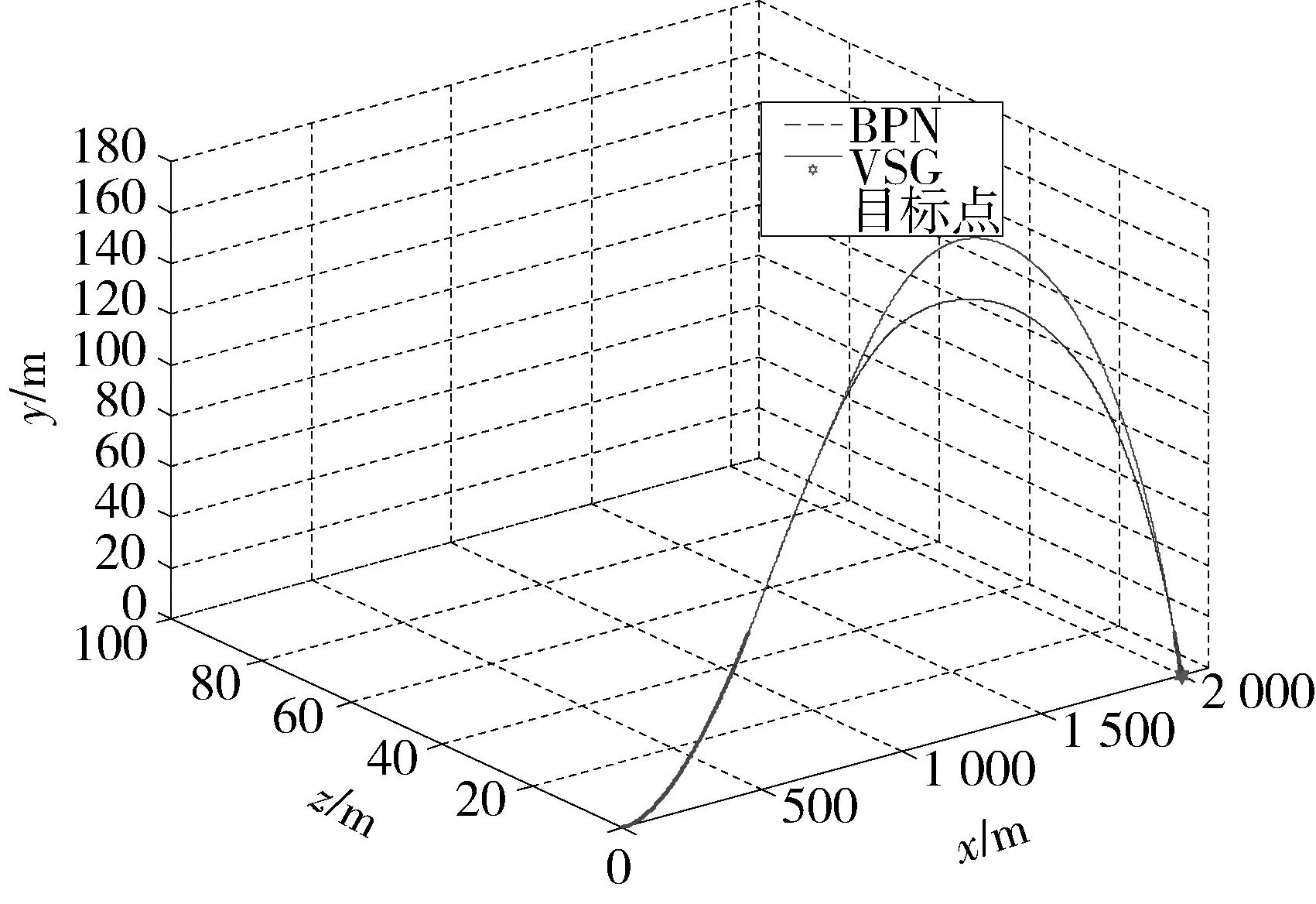
图3 导弹和目标相对运动轨迹Fig.3 Trajectory of missile and target
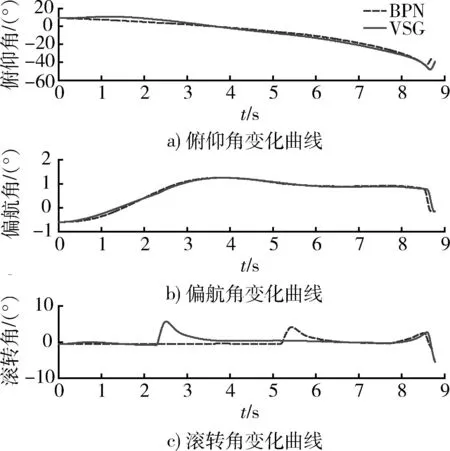
图4 导弹俯仰角、偏航角、滚转角变化曲线Fig.4 Changing of pitching angle, yaw angle, rolling angle
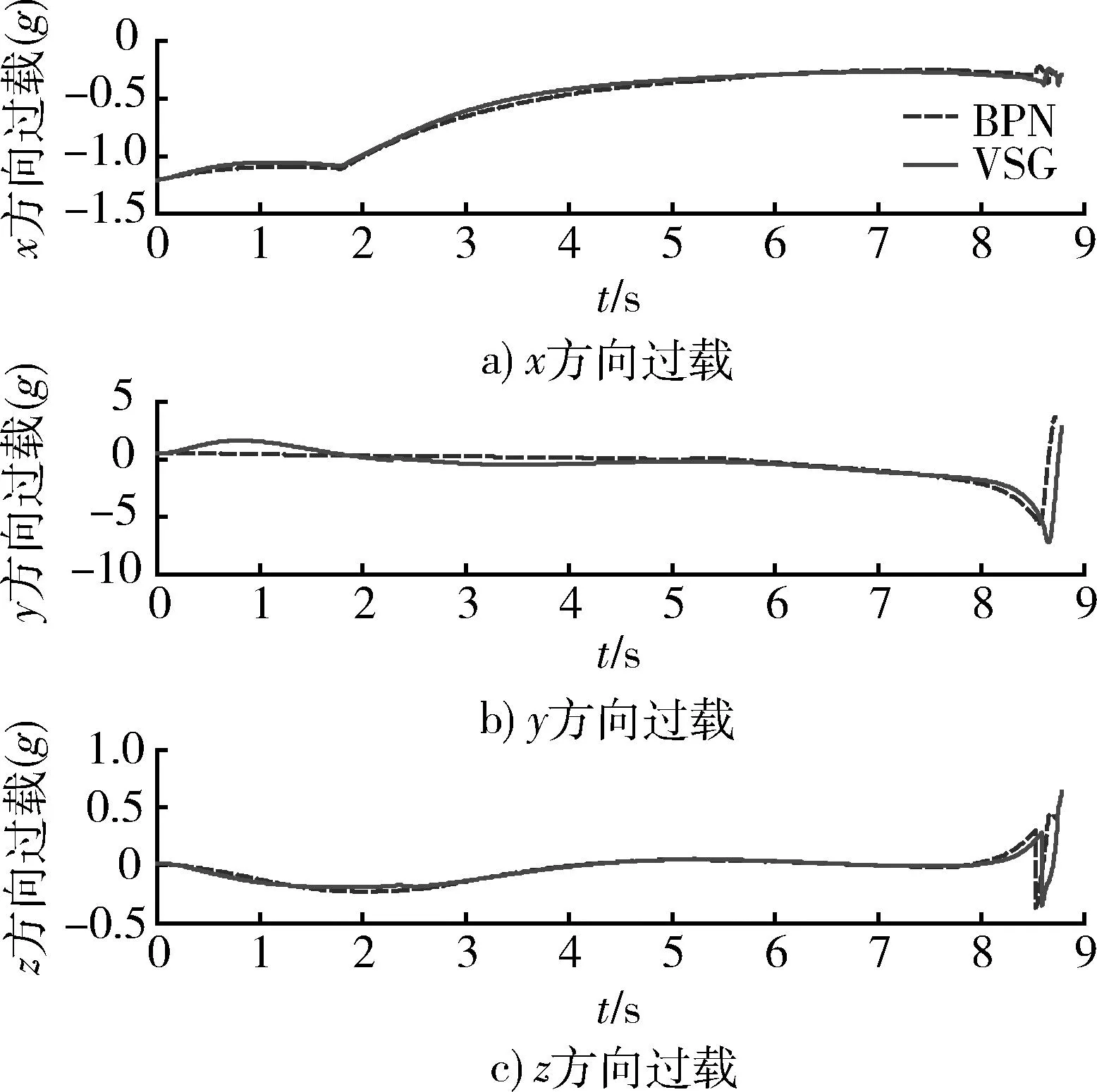
图5 导弹过载变化曲线Fig.5 Changing of missile overload
仿真场景2:目标为机动目标,在水平面内作蛇形机动;目标以20 m/s的速度沿Oz方向运动,沿Ox方向的加速度为atn=10 costm/s2,设定期望落角为 -50°。
其仿真结果如表2和图6~8所示。表2为针对机动目标,2种导引律算法制导性能的仿真结果对比。图6为导弹和目标在空间内的运动轨迹,目标沿z轴方向作蛇形机动。图7为导弹姿态角变化曲线,图8为导弹过载曲线,针对机动目标,VSG的末端过载相比BPN较大。

表2 场景2制导仿真结果
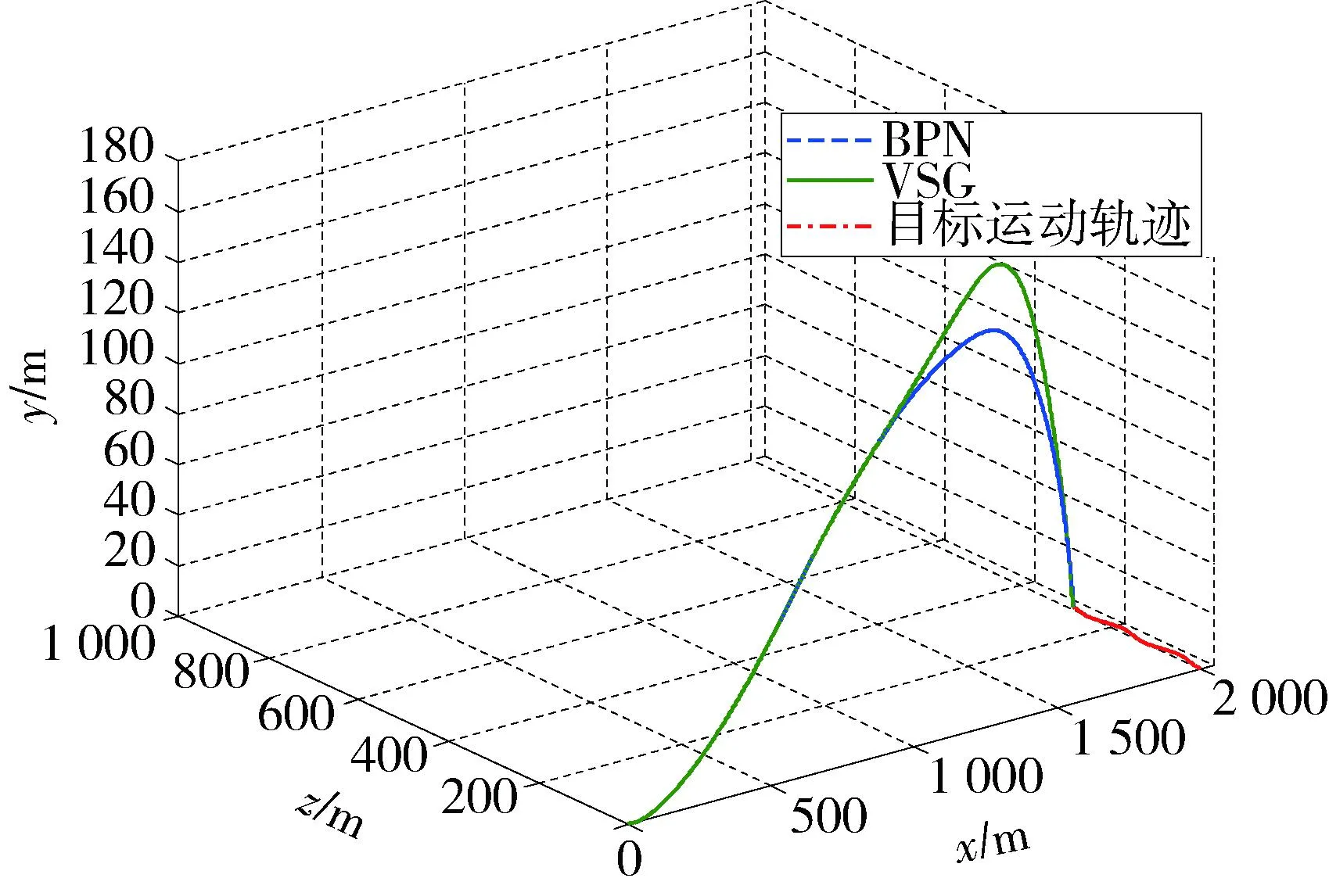
图6 导弹和目标相对运动轨迹Fig.6 Trajectory of missile and target
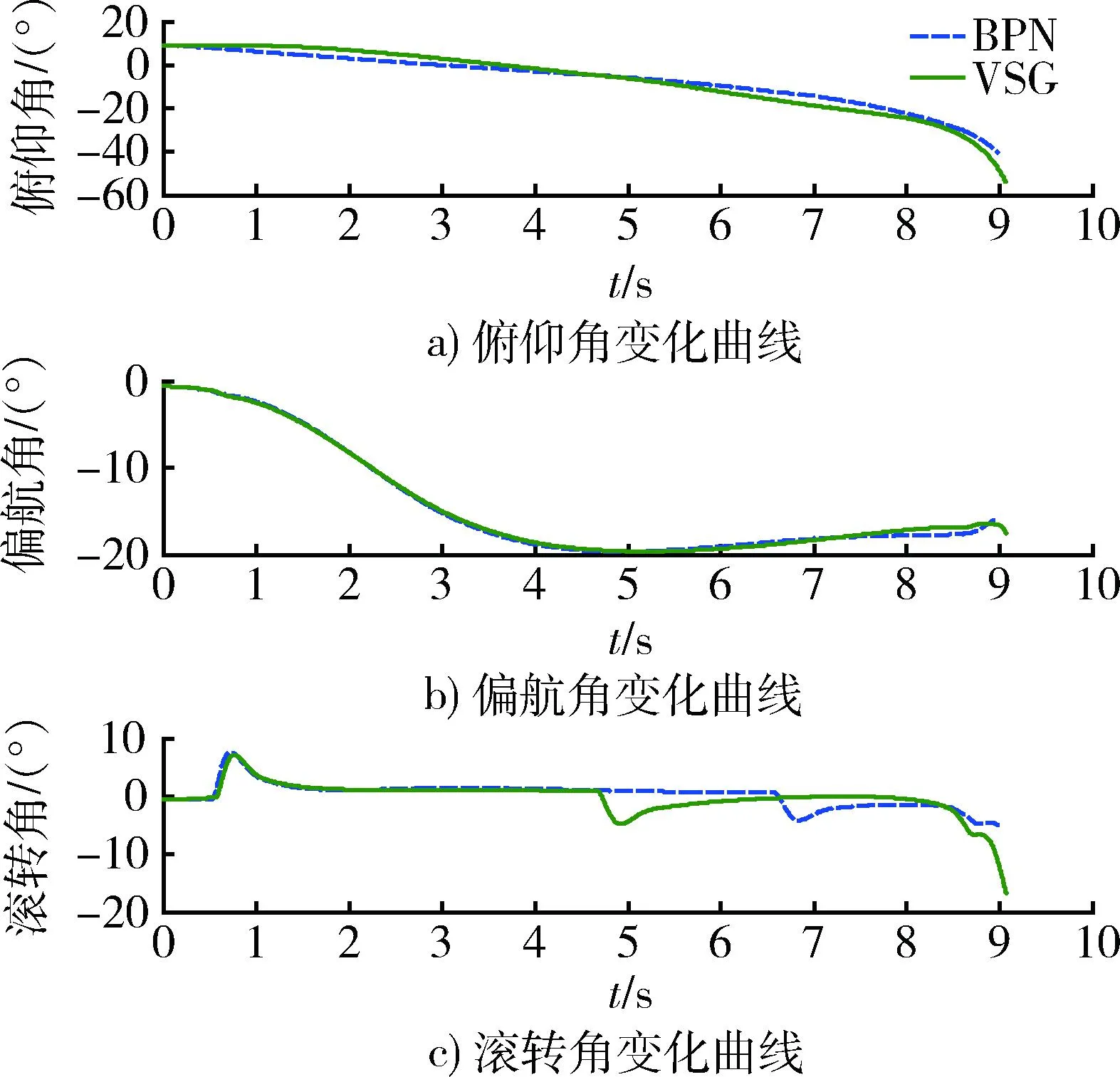
图7 导弹俯仰角、偏航角、滚转角变化曲线Fig.7 Changing of pitching angle, yaw angle, rolling angle
仿真场景3:目标为固定目标,期望落角分别为-30°,-50°,-70°,-80°。
仿真结果如表3所示。表3为针对固定目标,导弹在不同期望落角下,2种不同导引律作用时,产生的脱靶量、实际落角以及末制导时间等性能指标的对比仿真结果,可以看出,两者末制导时间基本一样,脱靶量和实际落角相差较大。
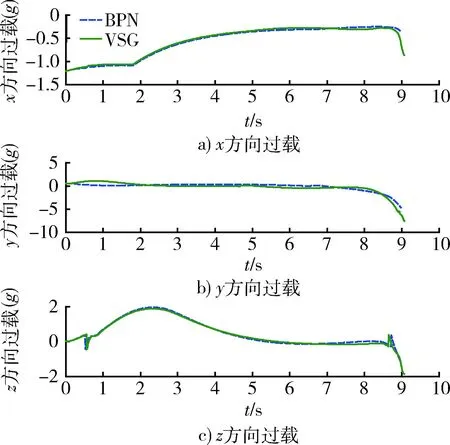
图8 导弹过载变化曲线Fig.8 Changing of missile overload

期望落角/(°)导引律脱靶量/m实际落角/(°)末制导时间/s-30BPN1.2332-28.77218.566VSG0.4195-30.74428.540-50BPN2.4382-43.56928.716VSG0.7595-48.33798.784-70BPN4.1829-60.75518.942VSG1.2954-69.05019.182-80BPN5.0846-69.14259.092VSG1.4941-77.98979.374
综合以上3种场景的对比仿真结果可以发现采用VSG和采用BPN制导过程所用时间基本一样,时间相差最大的也仅是VSG比BPN多用了0.28 s,因此VSG能够满足制导过程时间限定的要求。从图3和图6以及表1可以看出,采用VSG导弹的脱靶量最小为0.419 5 m,最大为1.494 1 m,对于反坦克导弹等精确命中打击武器而言,VSG能够很好满足导弹的命中精度要求。在相同的仿真环境下,采用BPN其脱靶量最小为1.233 2 m,最大为5.084 6 m,对于反坦克导弹等精确打击武器所打击目标的特征长度而言,此脱靶量明显很大,基本不能达到对目标的直接命中打击的目的。因此,无论对于固定目标和机动目标以及不同落角要求,VSG的制导精度明显优于BPN,同时也体现出了VSG对不同制导环境的适应性。
从图4和图7以及表1可以看出,在相同落角要求下,采用VSG得到的实际落角相比BPN更加接近期望落角,其落角误差明显更小,即使在期望大落角80°的情况下,依然能够满足落角约束要求,且仅相差2°。从图5和图8可以看出,采用VSG其对导弹的过载要求相比BPN基本一样,在末端略大于BPN,同时抖振现象得到了很好的抑制,因此,不需要对导弹性能提出更高要求。
通过3种场景的仿真实验结果可知,所提导引律对于固定和机动目标,都能以期望的落角命中目标,对机动目标具有很好的鲁棒性。
5结束语
本文选取相对速度偏角和落角约束条件作为滑模面,基于变结构控制理论提出了一种带落角约束的滑模变结构导引律,并证明了其稳定性,同时对其抖振进行了削弱,通过将其引入导弹实际模型进行对比仿真,结果表明,在不需提高导弹性能的前提下,针对固定目标和机动目标,其制导精度、落角约束和鲁棒性方面远优于比例导引律,能够大幅提高制导武器的制导性能,具制导律形式简单,具有很好的工程适用性。
参考文献:
[1]蔡洪,胡正东,曹渊. 具有终端角度约束的导引律综述[J]. 宇航学报,2010, 31(2):345-323.
CAI Hong, HU Zheng-dong, CAO Yuan. A Survey of Guidance Law with Terminal Impact Angle Constraints[J]. Journal of Astronautics, 2010, 31(2):345-323.
[2]KIM B S, LEE J G. Homing Guidance with Terminal Angular Constraint Against Non-Maneuvering and Maneuvering Target[R]. AIAA 1997-3474.
[3]Nathan Har, BALAKRISHNAN S N. Impact Time and Angle Guidance with Sliding Mode Control[R]. AIAA 2009-5897.
[4]尹永鑫,杨明,吴鹏. 针对机动目标带攻击角约束的三维制导律[J]. 固体火箭技术,2010, 33(3):237-241.
YIN Yong-xin, YANG Ming, WU Peng. Three-Dimensional Guidance Law with Attack Angle Constraint for Maneuverable Target[J]. Journal of Solid Rocker Technology, 2010, 33(3):237-241.
[5]WU Peng, YANG Ming. Integrated Guidance and Control Design for Missile with Terminal Impact Angle Constraint Based on Sliding Mode Control[J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 623-628.
[6]SHIMA T. Intercept-Angle Guidance[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 484-493.
[7]SHASHI R K, SACHIT R, DEBASISH G. Sliding-Mode Guidance and Control for All-Aspect Imterceptors with Terminal Angle Constraints[J]. Journal of Guidance, Control and Dynamics, 2012, 35(4): 1230-1246.
[8]ZHAO Yao, SHENG Yong-zhi. Sliding Mode Control Based Guidance Law with Impact Angle Constraint [J]. Chinese Journal of Aeronautics, 2014, 27(1): 145-152.
[9]郭鸿武,林维松,刘明俊. 基于相对速度偏角的变结构导引律[J]. 宇航学报,2001, 22(3):33-37.
GUO Hong-wu, LIN Wei-song, LIU Ming-jun. A Variable Structure Guidance Law Based on Relative Velocity Deflection Angle[J]. Journal of Astronautics, 2001, 22(3):33-37.
[10]林嘉新,赵永涛,胡云安. 基于零化相对速度偏角的变结构末制导律设计[J]. 海军工程学院学报,2009, 24(6):646-650.
LIN Jia-xin, ZHAO Yong-tao, HU Yun-an. Design of a Variable Structure Terminal Guidance Law Based on Relative Velocity Deflection Angle[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24(6):646-650.
[11]高为炳. 变结构控制的理论及设计方法[M]. 北京:科学出版社,1996.
GAO Wei-bing.Variable Structure Control Theony Design Method[M].Beijing:Science Press,1996.
[12]高峰,唐胜景,师娇,等. 一种改进的自适应滑模变结构导引律[J]. 弹道学报,2013, 25(3):18-23.
GAO Feng, TANG Sheng-jing, SHI Jiao, et al. An Improved Adaptive Sliding-Mode Navigation Guidance Law with Variable Structure[J]. Journal of Ballistics, 2013, 25(3): 18-23.
[13]张运喜,孙明玮,陈增强. 滑模变结构有限时间收敛制导律[J]. 控制理论与应用,2012, 29(11):1413-1418.
ZHANG Yun-xi, SUN Ming-wei, CHEN Zeng-qiang. Sliding-Mode Variable Structure Finite-Time Convergence Guidance Law[J]. Control Theory & Applications, 2012, 29(11):1413-1418.
[14]LEVANT A. Chattering Analysis[J]. IEEE Transactions on Automatic Control, 2010, 55(6):1380-1389.
[15]贾庆忠,刘永善,刘澡珍. 电视制导侵彻炸弹落角约束变结构反演制导律设计[J]. 宇航学报,2008, 29(1): 280-214.
JIA Qing-zhong, LIU Yong-shan, LIU Zao-zhen. Variable-Structure Back Stepping Guidance Law with Terminal Angular Constraint for Video Guided Penetrating Bomb[J]. Journal of Astronautics, 2008, 29(1): 280-214.
Adaptive Sliding Mode Variable Structure Guidance Law with Impact Angle Constraint
ZHANG Kuan-qiao, YANG Suo-chang, CHEN Peng, WANG Gang
(Ordnance Engineering College,Departmen of Missile Engineering,Hebei Shijiazhuang 050003, China)
Abstract:Aiming at the requirements of some guided weapons with attack accuracy and impact angle constraint, an adaptive sliding mode variable structure guidance law with impact angle constraint is proposed based on sliding mode variable structure control theory. Considering the rapid change of terminal line of missile-target sight angle sequence and the chattering phenomenon of variable structure, this guidance law chooses relative velocity deflection angle as the sliding mode, introduces the angular constraint, regards the target maneuvering as limited disturbance, and the stability of the guidance law is analyzed by using Lyapunov theory. Meanwhile, the chattering phenomenon is substantially weakened by the combination of variable switching term and saturation function. Finally, the simulation is made by applying the guidance law to the missile real model, and the results show that compared with traditional algorithm, the designed guidance law can hit the target with less miss distance and impact angle
Key words:guidance law; impact angle confinement; sliding-mode variable structure; relative velocity deflection angle; finite time convergence; adaptive approach law
*收稿日期:2015-01-26;修回日期:2015-06-25
作者简介:张宽桥(1992-),男,安徽蚌埠人。硕士生,主要研究方向为精确制导理论与技术。
通信地址:050003河北省石家庄市和平西路97号研3队E-mail:zkuanqiao@163.com
doi:10.3969/j.issn.1009-086x.2016.03.008
中图分类号:TJ765;TP202;TP391.9
文献标志码:A
文章编号:1009-086X(2016)-03-0044-08
导航、制导与控制

