一种基于卡尔曼滤波的动态相对位置解算算法*
孙海文,欧阳中辉
(海军航空工程学院 兵器科学与技术系,山东 烟台 264001)
一种基于卡尔曼滤波的动态相对位置解算算法*
孙海文,欧阳中辉
(海军航空工程学院 兵器科学与技术系,山东 烟台264001)
摘要:在舰船海上校飞过程中,测量解算飞机相对舰船的位置会产生一定的误差。采用直接算法在解算中没有对粗大误差和GPS信号缺失进行处理,解算结果误差较大。提出了一种改进的相对位置解算算法。通过仿真实验,从方位角、俯仰角和距离3个方面,对改进算法的解算精度和直接算法的解算精度进行分析比较,仿真结果表明,改进算法能很好的提高相对位置解算精度。
关键词:差分GPS;载波相位;动态相对定位;直接算法;基于卡尔曼滤波的相对位置解算算法;测量精度
0引言
在GPS定位研究的发展初期,主要使用C/A码伪距和P码伪距进行定位,其数学原理简单,定位速度可达到实时水平,但其定位精度不高。使用载波相位相对定位技术,因其高精度的定位能力,在国际上得到广泛的研究[1-4]。
在进行海上动态校飞真值获取时,不关心飞机在大地坐标系下的绝对位置,我们只关心飞机用户站待定坐标点相对于舰船基准站已知坐标点的位置,同时还要保证测量的高精度,这里使用载波相位相对定位技术进行坐标点位置获取,然后对目标相对位置的方位角、俯仰角及相对距离进行解算,采用传统的直接算法进行解算,不能处理粗大误差和GPS信号短暂缺失的问题,因此本文提出了一种基于卡尔曼滤波的动态相对位置解算算法。
1载波相位相对定位分析
利用载波相位DGPS进行相对定位的原理是:通过单点精密定位获取基准站的坐标,基准站将采集的载波相位观测值传送给用户站,然后进行双差解算获取用户站的坐标[5-8]。
如图1所示A,B为GPS的2个接收天线,把连接这2个天线的线段称为基线,称这个带有方向的基线为基线向量,记作P。在GPS姿态测量系统中,基线长度一般为几米到十几千米,而接收机与GPS卫星的距离约为20 000 km,所以由天线A和B指向同一颗GPS卫星的单位矢量可以看作是相同的,记为e。于是GPS信号的波前可以看作平面波。
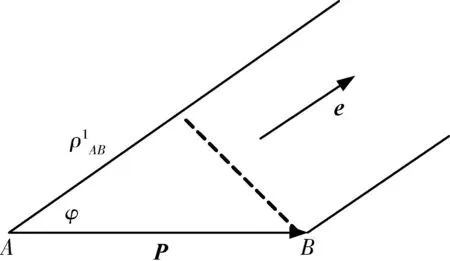
图1 姿态测量示意图Fig.1 Sketch map of attitude determination
从图1中的矢量三角形可以看出:
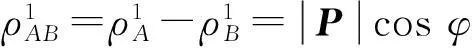
(1)
基准站首先把测得的GPS信号载波相位广播出来,用户接收到之后,和自己测得的对同一颗卫星的信号进行作差得
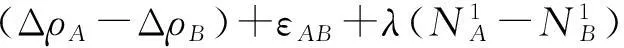
(2)
由于接收机A和B的距离相对于站星距来说很近,从卫星1发射出的电磁波到达接收机A与到达接收机B的传播环境是一样的,所受的电离层和对流层延迟也是相同的,进而式(2)可以简写为
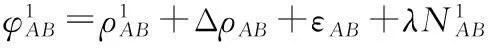
(3)
同理,对于GPS卫星2有如下等式:
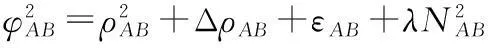
(4)
如果GPS接收机A和B能同时观测到的卫星数目大于或等于5颗(这里取5颗星,设为卫星1,2,3,4,5),同时设卫星1为主星,如果在用户接收机内把不同卫星的单差结果相互之间求差一次,便形成所谓的双差[10],则可以得到由4个载波相位双差方程组成的方程组,忽略残差的影响并写成矩阵的形式有

(5)
2坐标转换

以用户站天线坐标为例
(6)
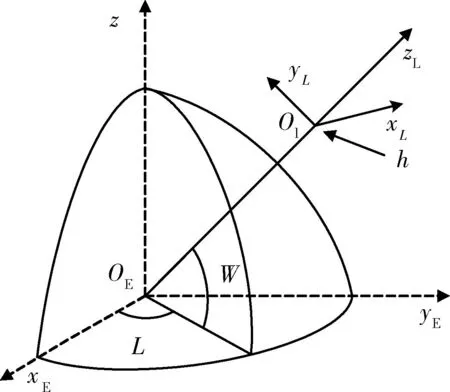
图2 转换关系示意图Fig.2 Sketch map of transformation relationship
(7)
式中:

(8)
3基于卡尔曼滤波的动态相对位置解算
建立水平坐标系,假设在舰船艉部架设基准站天线1,设为坐标原点,飞机上架设用户站天线2,建立如图3所示坐标系。
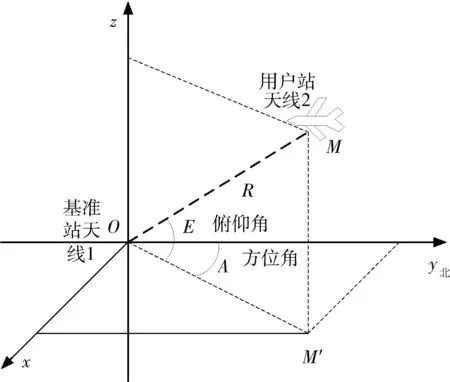
图3 水平坐标系下相对位置示意图Fig.3 Sketch map of horizontal coordinates relative position
利用载波相位DGPS进行动态相对定位解算时,采用直接法无法解决GPS信号缺失且不能反映出连续观测时各历元之间的关系,采用卡尔曼滤波[13-15]通过系统的状态转移方程可以反映出各历元之间在观测数据上的关系,并能解决GPS信号缺失问题。具体步骤如下:
假设飞机匀速飞行,建立卡尔曼滤波器基本模型,设状态向量为
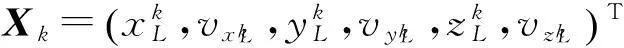
状态方程:Xk=Φk|k-1Xk-1+Γk-1Wk-1,
(9)
观测方程:Zk=HkXk+Vk,
(10)
状态转移矩阵Φk|k-1为

(11)
干扰矩阵Γk-1为
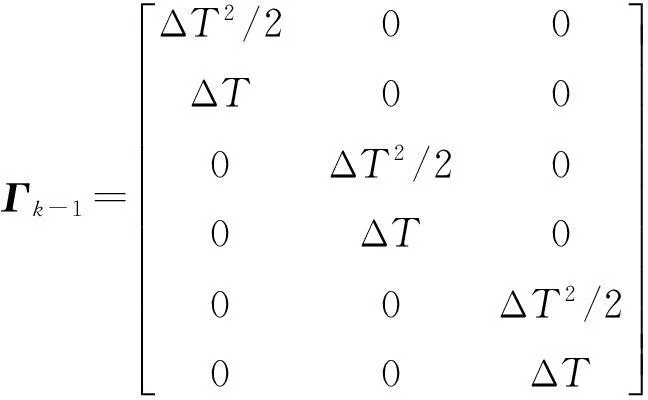
(12)
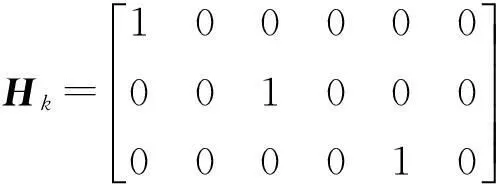
(13)
式中:ΔT为观测历元的时间间隔;Wk-1和Vk分别为系统激励噪声序列和系统噪声驱动序列,它们的特性为
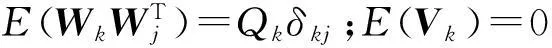
(14)
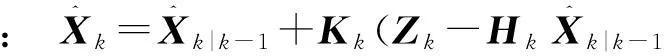
(15)
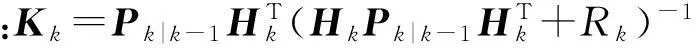
(16)
误差协方差预测方程:
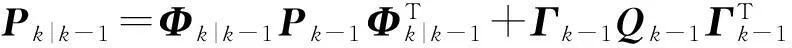
(17)
估计误差协方差方程:
Pk=(I-KkHk)Pk|k-1.
(18)
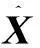
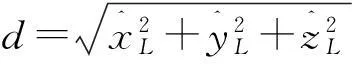
(19)
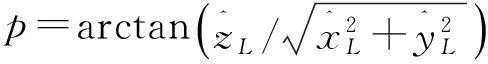
(20)
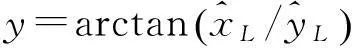
(21)
4仿真试验
4.1仿真条件建立
已知基准站和用户站的初始位置分别为(E37.941 694 44,N121.698 888 9,h15.134 256 72)、用户站为(E37.943 333 33,N121.730 833 3,h263.726 856 5),假设在水平坐标系下飞机相对舰船的速度(单位:m/s)在x,y和z轴上为
(22)
式中:T1和T2,T3和T4,T5和T6分别控制飞机相对舰船的速度在各坐标轴的变化周期。
4.2基于卡尔曼滤波的相对定位解算算法仿真结果分析
飞机与舰船相对位置随时间的关系如图4所示。从图4中可以看出10 s内飞机相对舰船俯仰角、方位角和距离的变化情况。
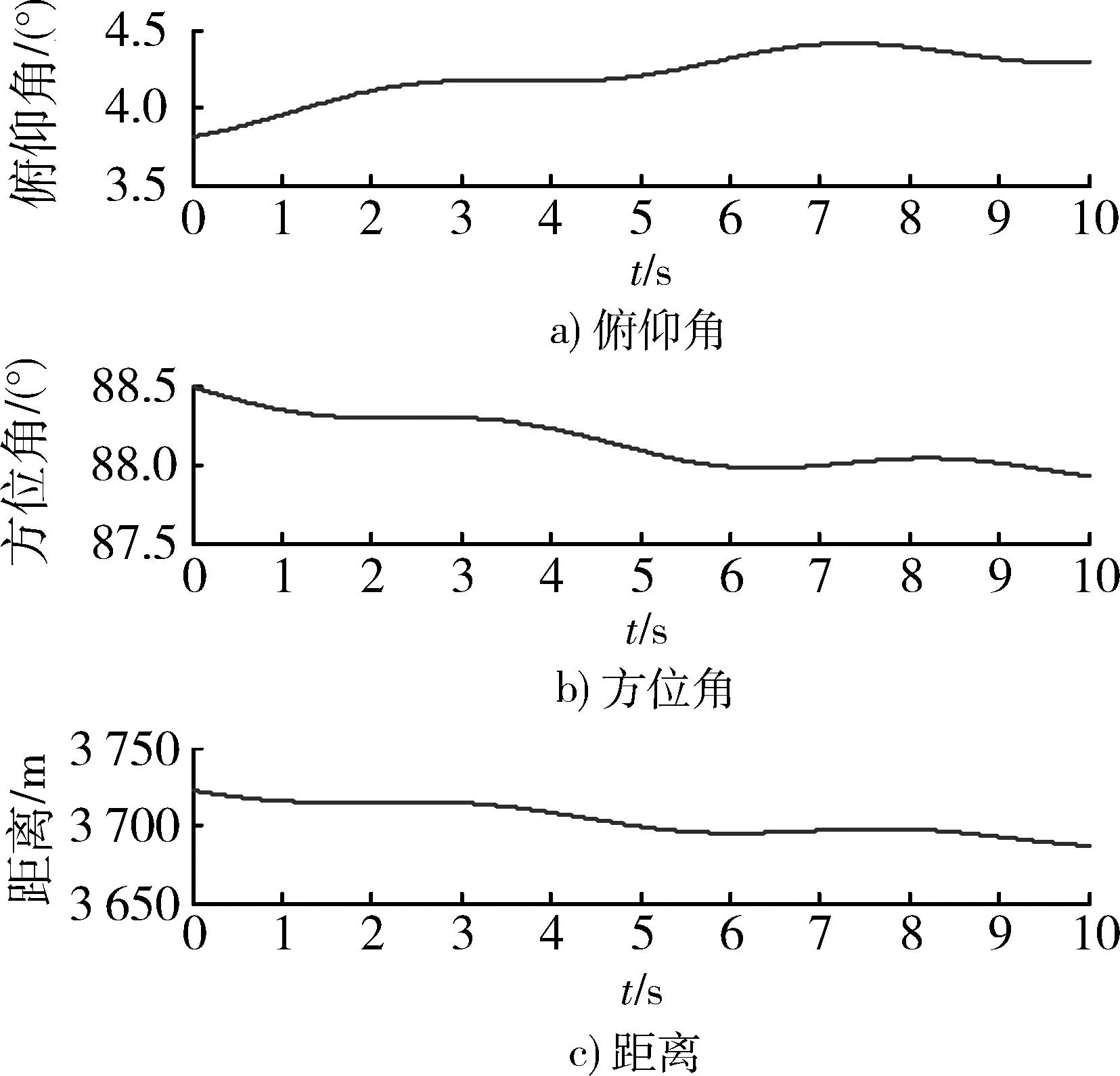
图4 飞机与舰船相对位置随时间的关系Fig.4 Relationship between the relative positionof aircraft and ships with time
从图4中可知,由于飞机相对舰船运动速度时刻不规则变化,因此得到的俯仰角、方位角和距离的变化存在不规则性。
引入随机噪声后用直接算法解算动态相对位置与基于卡尔曼滤波的动态相对位置解算法比较仿真结果如图5所示。
定性分析:从图5可见,基于卡尔曼滤波的动态相对位置解算算法能很好地消除粗大误差并能很好的补偿缺失数据,测量的相对位置精度明显提高。从图5a),5b)可知俯仰角和方位角时刻变化;从图5c)可知飞机正在接近舰船。
定量分析:从图6可见,直接算法计算出的方位角、俯仰角和距离的误差标准差分别为0.032,0.033,1.868;基于卡尔曼滤波的姿态解算算法计算出的方位角、俯仰角和距离的误差标准差分别为0.011,0.012,0.643。可以看出,基于卡尔曼滤波的动态相对位置解算精度明显优于直接法解算的精度。
利用Monte Carlo仿真方法,在随机噪声下进行1 000次仿真试验,分别得到改进法和直接法的方位角、俯仰角和距离的误差统计分布图,如图7所示。
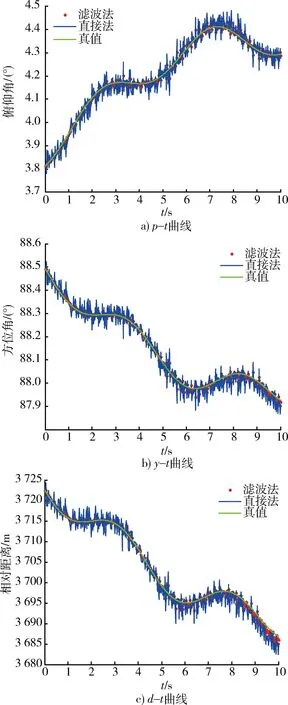
图5 2种算法动态相对位置仿真曲线图Fig.5 Curve map of dynamic relative position on two kinds of algorithm

图6 2种方法误差仿真曲线图Fig.6 Curve map of error of two methods
从图7可见,在多次仿真试验中,滤波法的解算误差明显小于直接法的解算误差,由此可知基于卡尔曼滤波的姿态解算算法能很好地提高解算精度。
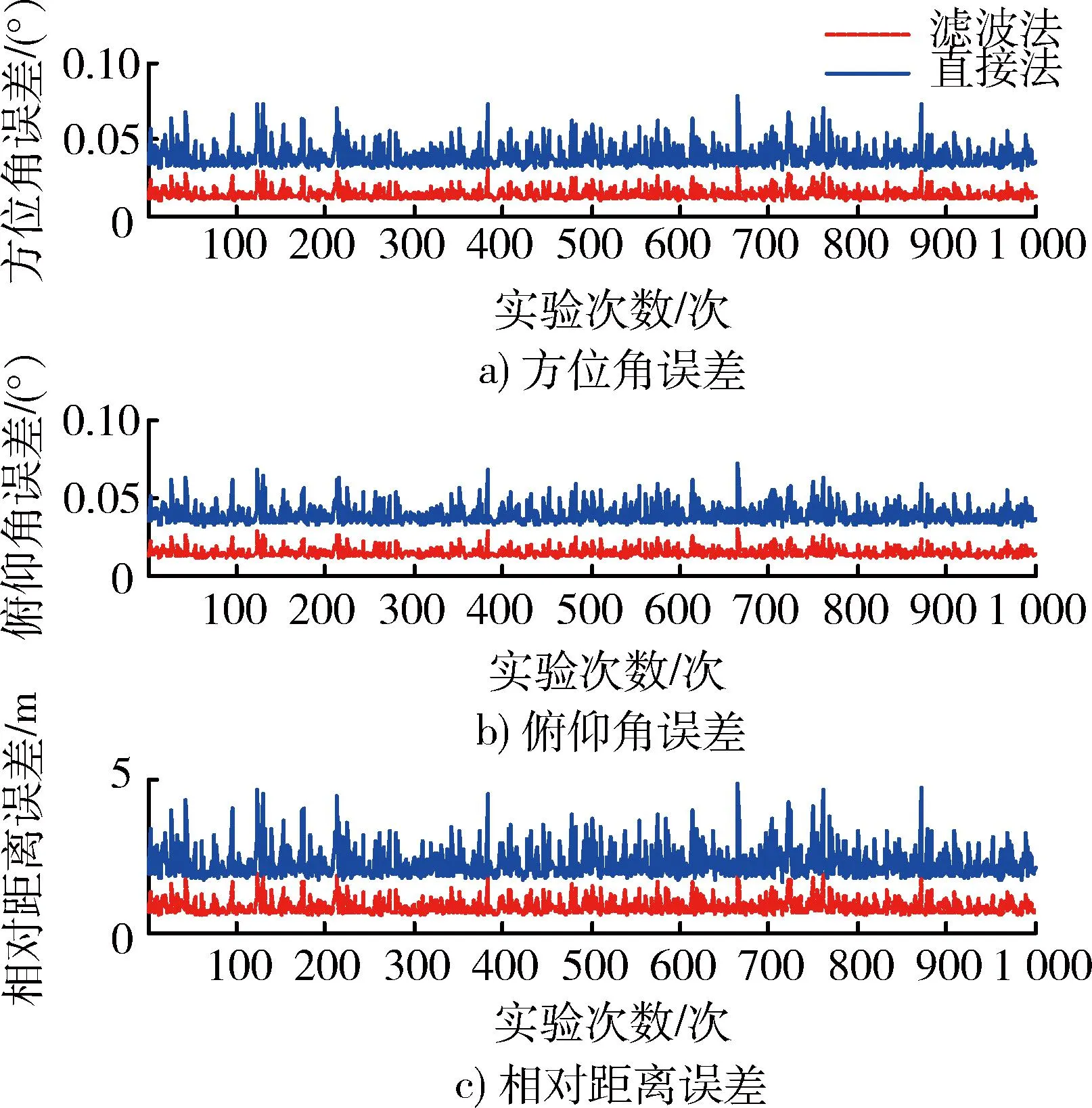
图7 2种方法误差统计分布图Fig.7 Statistics chart of error distribution of two methods
5结束语
本文对载波相位相对定位技术的原理进行阐述,再此基础上对获取的两GPS接收机的坐标点进行算法解算,这里提出了一种改进的动态相对位置解算算法即基于卡尔曼滤波的动态相对位置解算算法,它能消除粗大误差并且受GPS信号缺失的影响。通过仿真试验分析比较直接法与改进算法的测量精度,仿真结果表明改进算法比直接算法的解算精度高,解算效果好。
参考文献:
[1]刘大杰,施一民,过静珺.全球定位系统(GPS)的原理与数据处理[M].上海:同济大学出版社,1996:78-143.
LIU Da-jie,SHI Yi-min,GUO Jing-jun.The Global Positioning System (GPS) Theory and Data Processing [M].Shanghai:Tongji University Press,1996:78-143.
[2]周忠谟,易杰军,周琪.GPS卫星测量原理与应用 [M].修订版.北京:测绘出版社,1997:90-165.
ZHOU Zhong-mo,YI Jie-jun,ZHOU Qi. Measurement Principle and Application of GPS[M].Revised ed.Beijing:Surveying and Mapping Press,1997:90-165.
[3]张勤,李家权.GPS测量原理及应用[M].北京:科学出版社,2005.
ZHANG Qin,LI Jia-quan.Principle and Application of GPS Measurement [M].Beijing:Science Press,2005.
[4]胡伍生,高成发.GPS测量原理及其应用[M].北京:人民交通出版社,2002:75-78.
HU Wu-sheng,GAO Cheng-fa.GPS Measurement Principle and Application [M].Beijing:China Communications Press,2002:75-78.
[5]刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2003:216-317.LIU Ji-yu.GPS Satellite Navigation and Positioning Principle and Method [M].Beijing:Science Press,2003:216-317.
[6]李天文.GPS原理及应用[M].北京:科学出版社,2003:229-238.
LI Tian-wen.GPS Principle and Application [M].Beijing:Science Press,2003:229-238.
[7]王爱朝,张琰.GPS动态定位的初始化[J].测绘通报,1994,15(6):3-6.
WANG Ai-zhao,ZHANG Yan.GPS Dynamic Positioning to Initialize [J].Bulletin of Surveying and Mapping,1994,15(6):3-6.
[8]王仁谦.GPS动态定位的理论研究[D].长沙:中南大学,2004:7-10.
WANG Ren-qian.Theoretical Study of GPS Dynamic Positioning [D].Changsha:Central South Univercity,2004:7-10.
[9]李跃,邱致和.导航与定位[M].北京:国防工业出版社,2008:193.
LI Yue,QIU Zhi-he.The Navigation and Location [M].Beijing:National Defence Industry Press,2008:193.
[10]张守信.GPS技术与应用[M].北京:国防工业出版社,2004:101-120.
ZHANG Shou-xin.GPS Technology and Application [M].Beijing:National Defence Industry Press,2004:101-120.
[11]叶晓清.机载GPS实时精密定位技术研究[D].西安:西北工业大学,2004:4-8.
YE Xiao-qing.Research on Real Time Precise Positioning Technology of Airborne GPS [D].Xian Northwestern Polytechnical University,2004:4-8.
[12]程鹏飞,蔡艳辉,文汉江,等.全球卫星导航系统GPS,GLONASS,Galileo及其他系统[M].北京:测绘出版社,2007:209-211.
CHENG Peng-fei,CAI Yan-hui,WEN Han-jiang,et al.Global Navigation System GPS,GLONASS,Galileo and Other Systems[M].Beijing: Mapping Press,2007:209-211.
[13]KALMAN R E.A New Approach to Linear Filtering and Prediction Problems[J].Transaction of the ASME-Journal of Basic Engineering,1960,9(4):35-45.
[14]傅梦印.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.
FU Meng-yin.Kalman Filtering Theory and Its Application in Navigation System[M].Beijing:Science Press,2003.
[15]柳响林,刘经南,杜道生.卡尔曼滤波可靠性分析及其在动态GPS定位中的应用[J].武汉测绘科技大学学报,1997,22(3):234-237.
LIU Xiang-lin,LIU Jing-nan,DU Dao-sheng.Reliability Analysis of Calman Filter and Its Application in the Dynamic GPS Positioning[J].Journal of Wuhan University of Science and Technology of Surveying and Mapping,1997,22 (3):234-237.
An Algorithm of Dynamic Relative Position Based on Calman Filtering
SUN Hai-wen,OU-YANG Zhong-hui
(Naval Aeronautical and Astronautical University,Department of Ordnance Science and Technology,Shandong Yantai 264001,China)
Abstract:In the process of ship flying school, to compute the relative position of aircraft and ships will have a certain error. Direct algorithm of gross error and loss of GPS signaling processing make error in the calculation results. A relative position improved algorithm is proposed. Through the simulation experiment, for the three aspects of the azimuth angle, pitching angle and distance, the precision of calculation accuracy and direct algorithm improved algorithm are analyzed and compared. The simulation results show that, the improved algorithm can improve the relative position accuracy very much.
Key words:DGPS;carrier phase;dynamic relative positioning;direct method;algorithm of dynamic relative position based on calman filtering;measurement accuracy
*收稿日期:2015-05-04;修回日期:2015-07-07
作者简介:孙海文(1990-),男,山东烟台人。硕士生,研究方向为GPS标校。
通信地址:264001山东烟台芝罘区二马路188号二系1007室E-mail:m15666156198@163.com
doi:10.3969/j.issn.1009-086x.2016.03.006
中图分类号:TN967.1;TN713;TP312
文献标志码:A
文章编号:1009-086X(2016)-03-0032-06
导航、制导与控制

