临空高速目标模糊机动检测的IMM-EKPF算法*

付强，王刚，刘昌云，郭相科

(空军工程大学 防空反导学院，陕西 西安　710051)



探测跟踪技术

临空高速目标模糊机动检测的IMM-EKPF算法*

付强，王刚，刘昌云，郭相科

(空军工程大学 防空反导学院，陕西 西安710051)

摘要：针对临空高速目标运动状态多变，跟踪困难的问题，将扩展卡尔曼粒子滤波与交互多模算法相结合，提出IMM-EKPF算法，该算法不需要计算雅可比矩阵，能有效求解非线性非高斯环境的机动目标跟踪问题。在此基础上，有效结合模糊机动检测，可以在目标机动和非机动之间转换跟踪算法，以提高跟踪精度，减少计算量。仿真验证该方法在临空高速目标运动状态多变的情况下跟踪效果较好。

关键词：临空高速目标；信号融合；交互多模型算法；扩展卡尔曼粒子滤波；模糊机动检测；目标跟踪

0引言

临空高速目标的运动状态不固定，在机动与非机动之间不确定的变换，对稳定跟踪技术提出巨大挑战。扩展卡尔曼滤波(extended Kalman filter, EKF)在接近线性的模型中被经常使用，但在机动目标跟踪中，系统及观测模型是非高斯及非线性的，EKF算法效果不令人满意。粒子滤波(particle filter, PF)思想是用样本形式来描述先验及后验信息[1-2]，随着样本的增加，粒子滤波估计接近最优贝叶斯估计，但存在退化现象，一种改进的方法是选择合理的建议分布函数[3]。在研究建议分布函数构造的基础上，Freitas提出扩展卡尔曼粒子滤波算法[4](extended Kalman particle filter, EKPF)，可利用EKF算法，使粒子分布接近后验概率分布，同时减少粒子的使用个数。与滤波模型一样，机动模型的选择也是机动目标跟踪难题，交互多模型(interactive multiple model, IMM)算法使用马尔可夫过程描述模型之间的切换[5]。

本文将EKPF和IMM算法相结合，提出交互多模型扩展卡尔曼粒子滤波算法(interactive multiple model-extended Kalman particle filter, IMM-EKPF)，由于不需要计算雅可比矩阵，针对非线性非高斯环境的机动目标具有很好的跟踪效果。IMM-EKPF与EKF相比计算量过大，当临空高速目标处于非机动时，EKF能够在保证跟踪精度的条件下减少计算量。既而提出结合模糊机动检测，其思想是首先对残差进行平滑，消除随机误差影响，再对平滑残差及残差变化值进行模糊化处理，推理目标发生机动的概率。设置机动门限，当机动概率大于门限值时，认定目标发生机动，使用IMM-EKPF，反之，使用EKF。

本文方法能够在确保跟踪精度的前提下减少计算量，针对临空高速目标有很好的适用性。

1EKPF算法

标准的粒子滤波最常见的问题就是粒子退化问题，避免退化的方法主要是重采样算法[6]。这里采用粒子滤波和扩展卡尔曼结合的算法，即考虑到最近观测信息的影响。

EKPF依据蒙特卡罗方法，通过使用一定的加权粒子来拟合状态空间中状态向量服从的概率密度函数，并且通过贝叶斯理论使用观测值修正加权粒子的权值，最优状态估计值为粒子的加权求和，把方差和最优估计值传给扩展卡尔曼滤波方程完成处理，对滤波精度有整体的提高[7]。

设初始状态变量x0服从p(x0)分布，EKPF算法流程如下：

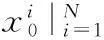
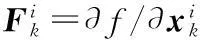
(1)

(2)

(3)

(4)

(5)

Step 3： 根据公式计算N个粒子对应的权值，并且将这些粒子的权值做归一化处理；

Step 4： 通过重采样计算得出重采样后的粒子和权值；

Step 5： 分别计算每个粒子相应的方差矩阵和状态变量的最优估计；

Step 6： 将Step 4中完成重采样的粒子及Step 5中计算得出的方差阵代入到Step 2中完成迭代运算。

2IMM-EKPF算法

在机动目标跟踪算法中，交互多模型算法是一种性能较好的算法，因为多种模型的交互作用，使得目标在做不同形式的运动时，可以更好的符合其真实状态。将扩展卡尔曼粒子滤波与交互多模算法相结合，可以适应于非线性非高斯环境的机动目标跟踪。算法循环包括：交互运算、滤波、更新模型概率以及融合输出等[8]。

(1) 交互运算

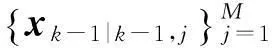
(6)

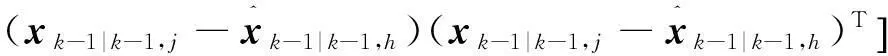
(7)

(2) 滤波

粒子预测

(8)

(9)

(10)

计算残差

(11)

(3) 模型概率更新

计算模型的似然函数

Sk,j=

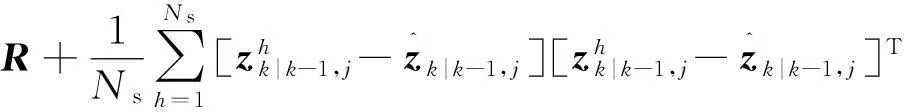
(12)

(13)

各模型概率更新

(14)

(4) 融合输出

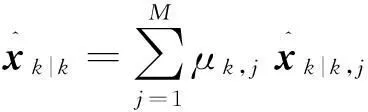
(15)

3基于平滑残差的模糊机动检测

临空高速目标实际运动状态在机动及非机动2种模式之间变化，一般可以用多个机动模型和一个非机动模型来描述，如图1所示。通常滤波算法的跟踪性能与使用的模型和实际运动状态的匹配程度有很大关系。

图1　改进算法示意图Fig.1　Schematic diagram of improved algorithm

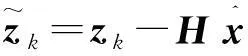
图2某一机动目标跟踪中各个时刻的残差值加权。由于参数及系统噪声等不确定性因素的影响，使得原始残差值波动范围较大，导致机动检测有很多误判断。

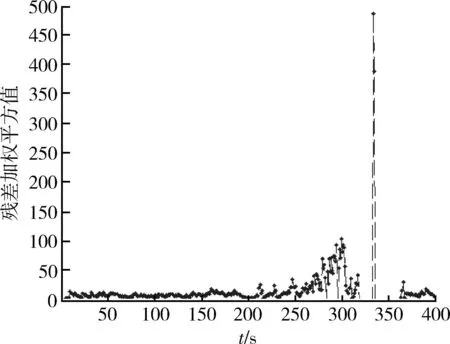
图2　加权平方后的残差值Fig.2　Residual value of the weighted square

图3　平滑残差值Fig.3　Smoothed residuals

图4为残差平滑前及平滑后的比较。可见，平滑方法能够较好的消除了随机误差带来的影响，可以较好的体现机动特性。

图4　残差平滑前后值比较Fig.4　Comparison of residual smoothing

对于平滑残差，能够较好避免随机检测的错误，然而普遍存在比较明显的滞后效应，即目标发生机动一段时间后，残差值才超过门限值。这一点影响了跟踪性能，当目标进行强机动时，较大的延时通常会使丢失目标[11]。

通过平滑残差曲线能够看出，目标在发生机动之前，数值较为稳定的随机波动，当目标机动时，平滑残差值在不断增加，直到大于门限。虽然需要一段时间平滑残差值才能超过门限，但在机动开始后，平滑残差值是一直增加的且变化规律较为稳定[12]。

若在算法中将此判断信息引入，对提高机动跟踪的准确性和实时性有明显帮助，这一思想可以通过模糊推理过程来实现。

在整个算法中，用模糊推理来进行机动跟踪，依据当前残差变化和平滑残差值，算出该时刻使用IMM-EKPF的概率，当此概率大于设定的门限时，使用IMM-EKPF，否则使用EKF。

3.1模糊化平滑残差

首先将输入变量完成模糊化，算法中输入包括当前平滑残差ek以及平滑残差的变化dek。平滑残差ek可以通过计算移动窗口的平均残差值得到[13]， dek=ek-ek-1为平滑残差变化值，dek如图5所示。将平滑残差变化值以及平滑残差做模糊化处理，残差变化值的模糊集合定义为：负、零、正；平滑残差值的模糊集合定义为：小，中，大。隶属度函数为梯形，如图6所示。

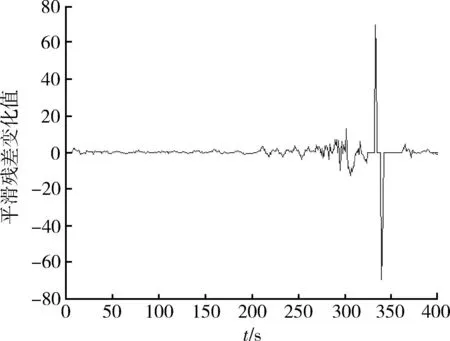
图5　平滑残差变化值图Fig.5　Smoothed residual variation chart

图6　梯形隶属度函数Fig.6　Trapezoidal membership function

3.2模糊推理与解模糊

模糊推理采用TS方法，对于2输入1输出系统的模糊控制规则，其基本形式为

ifekisAand dekisB,thenp=C

平滑残差以及残差变化值的模糊集合分别为A,B，目标机动的概率值为C。

显而易见，当平滑残差的模糊变量为“大”并且残差变化的模糊变量为“正”时，机动的概率最大，可设为1，其他情况可以此逻辑类推。通过输入的残差、残差变化量和隶属函数可以得到如表1所示的模糊推理规则，P(k)为目标机动的概率。

表1　模糊推理规则

4带模糊机动检测的跟踪算法

使用模糊机动检测，使得跟踪算法可以在机动和非机动之间转换，检测到机动时，使用IMM-EKPF算法，以提高机动时的跟踪精度；而非机动时，采用普通的EKF算法，在保证跟踪精度的情况下，尽量减少计算量。算法的整体流程图如图7所示。

图7　算法流程图Fig.7　Algorithm flow chart

为了验证滤波跟踪算法的有效性，现使用Matlab对其进行仿真。假设算法中采用的量测方程和状态方程为

(16)

设采样周期T为2，检测机动的有效窗口长度为5，门限值Th为0.6[15]，粒子数目为50，进行50次蒙特卡罗仿真。本文的仿真选取弱机动和机动的情况进行仿真实验。首先假设目标的运动状态如表2所示。目标的初始位置是(2 000，10 000)，进行匀速运动和匀加速运动的交替运动，速度和加速度都很小，机动性较弱。

由以上假设进行仿真，其中图8表示目标的真实轨迹与观测轨迹，图9表示残差值、残差平滑的对比，图10表示平滑残差值的变化值，图11表示每个时刻模糊推理得到的机动概率结果，图12表示目标真实轨迹与50次滤波轨迹的比较结果。

由目标的运动状态可知，在采样时间为200时，目标加速机动，在之后的时间段内，都处于机动状态，直到时间为330左右，才恢复匀速运动。由模糊机动检测得到的机动概率值在目标加速时有所体现，但是值不大，表明目标正在进行的是弱机动，由图11模糊推理结果可知，本文算法得到的机动检测结果是可信的。

表2　目标真实运动状态

图8　真实轨迹与观测轨迹Fig.8　True trajectory and observation trajectory

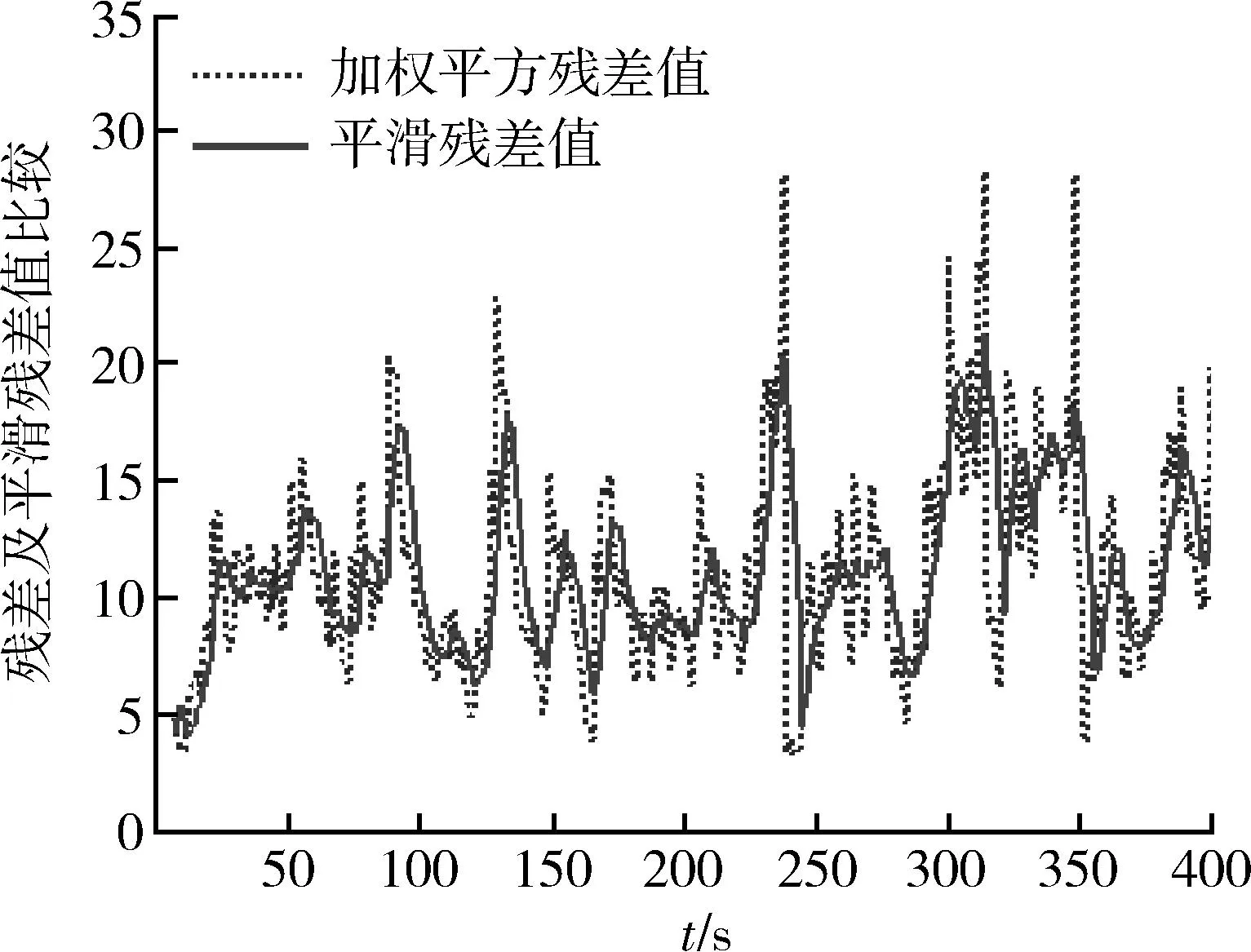
图9　加权平方残差及平滑残差值比较Fig.9　Comparison of weighted squared residuals and smoothed residuals

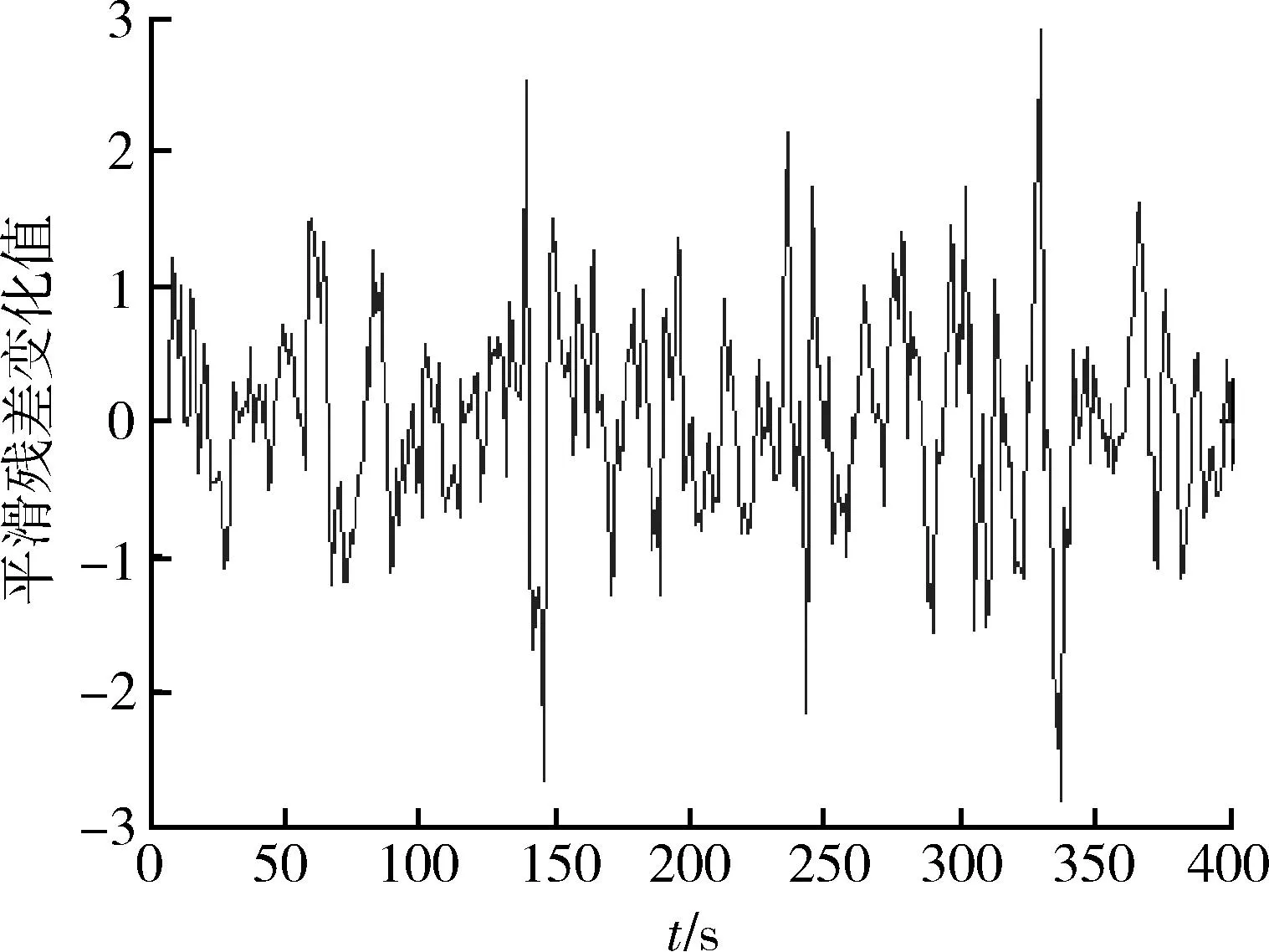
图10　平滑残差变化值Fig.10　Smoothed residual variation

图11　任意时刻模糊推理结果Fig.11　Fuzzy reasoning results at any time

由图12可以看出本文方法适用性较好，在目标强机动时滤波轨迹会产生一定偏差，但很快就与真实轨迹拟合。

图12　真实轨迹与滤波轨迹比较Fig.12　Comparison between real and filtered navigation

本文选取做转弯机动的目标进行对机动情况滤波效果的检测。假设目标运动状态如表3所示，进行仿真。本例的目标状态相对上例，机动性较强。图13表示残差值、残差平滑值，图14表示平滑残差值的变化值，图15表示x和y坐标的滤波误差均值曲线及标准差曲线，图16表示真实轨迹与50次滤波轨迹的比较。

表3　目标真实运动状态

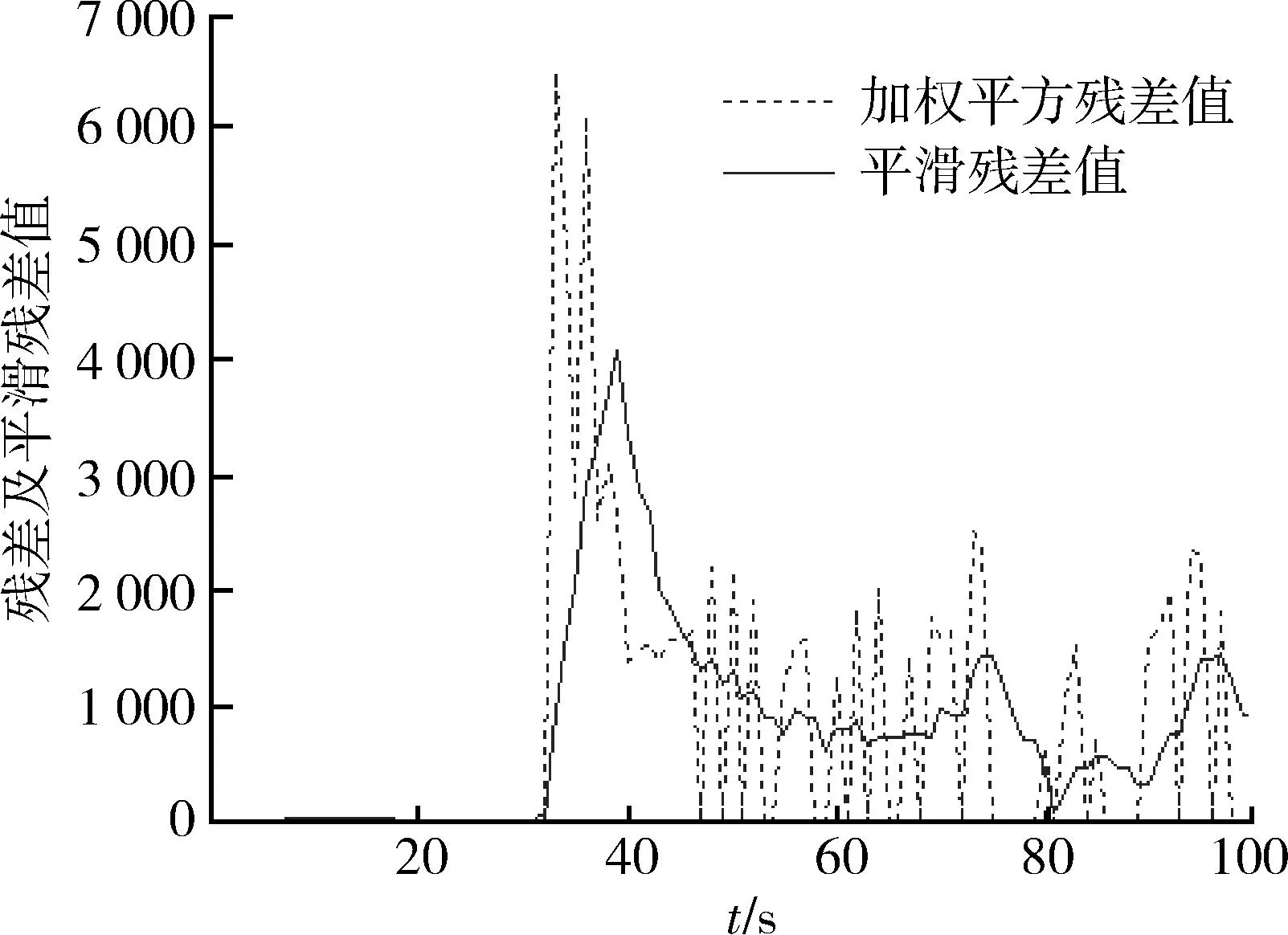
图13　残差及平滑残差值Fig.13　Residuals and smoothed residuals

图14　平滑残差变化值Fig.14　Smoothed residual variation

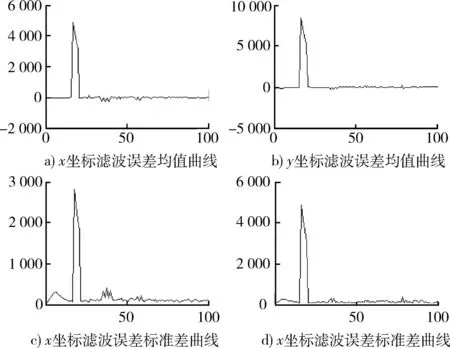
图15　x和y坐标滤波误差均值及标准差曲线Fig.15　x and y coordinates of the filter error mean and standard deviation curve

图16　真实轨迹与滤波轨迹比较Fig.16　Comparison between real trajectory and filter trajectory

由图16可以看出，经过50次滤波后的轨迹与真实轨迹非常逼近，目标匀速转弯时能够稳定跟踪，有效验证了结合模糊机动的IMM-EKPF算法在临空高速目标跟踪中具有很好的性能。

5结束语

本文首先将平滑残差进行模糊推理，判定目标是否机动。当目标机动时，提出IMM-EKFP算法，该算法能有效解决非高斯非线性环境下目标跟踪问题，目标不机动时，运用传统EKF算法，保证跟踪性能的前提下减少计算量。最终通过真实航迹与滤波航迹的比较，验证该方法针对临空高速目标跟踪效果显著。

参考文献：

[1]WANG X, CHEN J F, SHI Z G, et al. Fuzzy-Control-Based Particle Filter for Maneuvering Target Tracking[J]. Progress In Electromagnetics Research,2011, 118(3): 1-15.

[2]FARAHMAND S, ROUMELIOTIS S I, GIANNAKIS G B. Set-Membership Constrained Particle Filter: Distributed Adaptation for Sensor Networks [J].IEEE Transactions on Signal Processing, 2011, 59(9): 4122-4138.

[3]HUANG Jin-wang，FENG Jiu-chao. Signal Reconstruction in Wireless Sensor Networks Based on a Cubature Kalman Particle Filter[J]. Chinese Physics B, 2014, 36(7): 1213-1216.

[4]李锋, 解少飞, 毕志献. 高超声速飞行器中若干气动难题的实验研究[J]. 现代防御技术, 2014, 42(5): 369-375.LI Feng,XIE Shao-feng,BI Zhi-xian. Experimental Study on Aerodynamic Problems of High-Speed Vehicle[J].Modern Defense Technology,2014, 42(5):369-375.

[5]LIAO T, STUTZLE T, de Oca M A M. A Unified Ant Colony Optimization Algorithm for Continuous Optimization[J]. European Journal of Operational Research, 2014, 234(3):597-609.

[6]LI X R, JILKOV V P. A Survey of Maneuvering Target Tracking Part V: Multiple-Model Methods[J].IEEE Trans. on Aerospace and Electronic Systems,2005, 41(4): 1255-1321.

[7]侯静, 景占荣, 羊彦. 远距离干扰环境下目标跟踪的扩展卡尔曼粒子滤波算法[J].电子与信息学报, 2013, 35(7): 1587-1592.

HOU Jing,JING Zhan-rong,YANG Yan. Extended Kalman Particle Filter Algorithm for Target Tracking in Stand-off Jammer[J].Journal of Electronics & Information Technology, 2013, 35(7): 1587-1592.

[8]王华剑. 基于改进扩展卡尔曼粒子滤波的目标跟踪算法[J].计算机应用研究, 2011, 28(5): 1634-1639.

WANG Hua-jian. Target Tracking Algorithm Based on Improved Extend Kalman Particle Filter[J]. Application Research of Computers, 2013, 35(7): 1587-1592.

[9]江宝安,万群. 基于UKF-IMM的双红外机动目标跟踪算法[J]. 系统工程与电子技术, 2008, 30(8): 1454-1459.

JIANG Bao-an,WAN Qun. Maneuvering Target Passive Tracking with Dual Inferred Observer Using IMM Algorithm Based on UKF[J]. Systems Engineering and Electronics, 2008, 30(8): 1454-1459.

[10]MOHAMMADI A, ASIF A. Consensus-Based Distributed Unscented Particle Filter[C]∥IEEE Statistical Signal Processing Workshop (SSP), Nice, 2011: 237-240.

[11]YANG W, FU Y W, LI X. Joint Target Tracking and Classification Via RFS-Based Multiple Model Filtering [J].Information Fusion, 2013, 18(3), 101-106.

[12]徐洋, 徐松涛, 罗文涛. 基于虚拟检测函数下的IMM-UKF机动目标跟踪[J]. 火力与指挥控制, 2015, 40(1): 37-41.

XU Yang,XU Song-tao,LUO Wen-tao.IMM-UKF Maneuvering Target Tracking Based on Virtual Detection Function[J]. Fire and Command Control, 2015, 40(1): 37-41.

[13]EN F, WEI X X, ZONG X L. Maneuvering Target Tracking Using Fuzzy Logic-Based Recursive Least Squares Filter [J]. EURASIP Journal on Advances in Signal Processing, 2014, 53(1):1-9.

[14]Ahmadreza, Amirzadeh, Ali Karimpour. An Interacting Fuzzy-Fading-Memory-Based Augmented Kalman Filtering Method for Maneuvering Target Tracking[J]. Digital Signal Processing,2013, 23(5): 1678-1685.

[15]DONG L P, YUN F G. Fuzzy-Logic Adaptive Variable Structure Multiple-Model Algorithm for Tracking a High Maneuvering Target[J]. Journal of the Franklin Institute，2013, 21(9)：11-21.

Near Space High-Speed Targets Fuzzy Maneuvering Detection with IMM-EKPF Algorithm

FU Qiang, WANG Gang, LIU Chang-yun, GUO Xiang-ke

(AFEU, Air and Missile Defense College, Shaanxi Xi’an 710051, China)

Abstract:Aiming at the issue that it is difficult to trace variable motion states of near space high-speed targets, the extend Kalman particle filter (EKPF) and interaction multiple model (IMM) are combined to develop an interaction multiple model-extend Kalman particle filter (IMM-EKPF) algorithm. The algorithm needs not to calculate the Jacobi matrix, and it can effectively solve non Gauss and non-linear target trace. On this basis, combined with fuzzy maneuvering detection, rack algorithm is transitioned between maneuvering and non-maneuvering to improve the tracking accuracy and reduce the amount of calculation. Results demonstrate the feasibility of this method.

Key words:near space high-speed target; signal fusion; interaction multiple model; extend Kalman particle filter; fuzzy maneuvering detection; target trace

*收稿日期：2015-04-20；修回日期：2015-07-07

基金项目：国家自然科学基金项目(61272011); 国家自然科学青年基金(61102109)

作者简介：付强(1988-)，男，陕西西安人。博士生，主要研究方向为智能信息处理。

通信地址：710051陕西省西安市长乐东路空军工程大学防空反导学院E-mail：fuqiang_66688@163.com

doi:10.3969/j.issn.1009-086x.2016.02.023

中图分类号：TN957.51；TP391.9

文献标志码：A

文章编号：1009-086X(2016)-02-0143-08