基于阵列天线的归一化变步长抗干扰算法研究*

袁鑫，吴荣刚，孙武，蒋清富

(北京遥感设备研究所,北京　100854)



基于阵列天线的归一化变步长抗干扰算法研究*

袁鑫，吴荣刚，孙武，蒋清富

(北京遥感设备研究所,北京100854)

摘要：针对阵列天线的自适应抗干扰方法，研究了线性约束最小方差(LCMV)算法，并对其收敛性进行分析，提出归一化变步长线性约束最小方差(LCMV)算法。该方法解决了定步长自适应算法收敛速度和稳态误差不能同时满足的难题，避免了协方差矩阵求逆运算，减小了运算量，便于工程实现。通过仿真和实验表明，该算法收敛速度快，能在干扰方向上形成很深零陷，干扰抑制效果好。

关键词：自适应；阵列天线；收敛速度；稳态误差；线性约束最小方差；抗干扰

0引言

近年来，自适应阵列天线技术广泛的应用在卫星导航领域，用于对抗敌方人为的干扰，从而提高军事武器的精确打击能力。该技术根据信号和干扰的实际环境灵活地控制各个天线阵元的加权参数，自动调节天线方向图的形状，在不影响有用信号增益的前提下，对干扰进行有效的调零抑制。而自适应抗干扰算法是整个自适应天线技术的核心内容，成为大家普遍关注的重点[1-2]。

基于阵列天线的空域自适应处理是有效的自适应抗干扰算法，但是由于空域处理本身自由度的限制，当存在大量宽带干扰和窄带干扰时，采用空域处理需要更多的天线阵列，花费太大。空时自适应处理[3](space-time adaptive processing,STAP)联合空域处理和时域处理的优点，在不增加天线阵元的情况下，通过时间抽头来增加阵列天线自适应处理的自由度以抑制大量窄带干扰，宽带干扰和色散多径干扰[4]，但是这种处理方法需要求解协方差矩阵的逆，抽头数越多，矩阵维数越大，逆运算复杂度越高，实时性很难保证。因此一系列不需要数据存储，计算量小的递推算法[5]应运而生。

常用的自适应算法有最小均方误差(LMS)算法[6-7]和递推最小二乘(RLS)算法[8]。RLS算法直接对协方差矩阵的逆进行递推估计更新，收敛速度快，但是计算复杂度高，存储量大，不利于实时实现；LMS算法结构简单，鲁棒性强，计算量小，但是收敛速度慢，稳定性差。本文在线性约束最小方差LCMV算法的基础上分析算法性能，提出归一化变步长LCMV算法，提高其收敛速度，减小稳态误差，实施性强，并模拟真实干扰进行仿真验证。

1LCMV算法

空时自适应算法处理结构[9-10]如图1所示。天线阵共有M个阵元，每个阵元通道后有一个N阶FIR滤波器，FIR滤波器各抽头输入信号如图1所示。

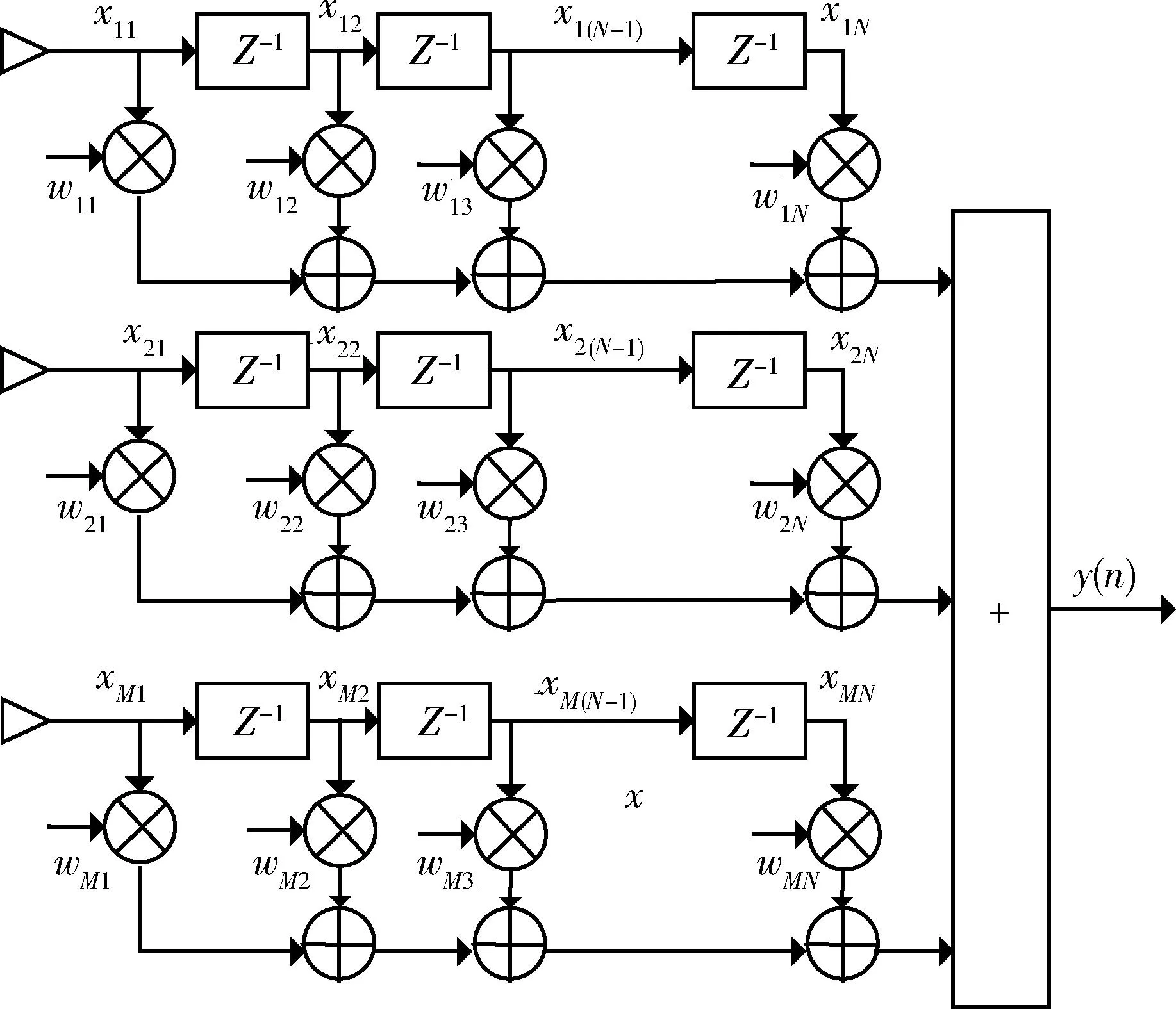
图1　空时自适应算法处理结构图Fig.1　Functional block diagram of adaptive pace-ime processing

用x表示输入信号矩阵为

x=(x11,x12,…,x1N,x21,x22,…,x2N,…,xM1,xM2,…,xMN)T.

(1)

用MN×1维向量w表示处理器权矢量，则

w=(w11,w12,…,w1N,w21,…,w2N,…,wM1,…,wMN)T.

(2)

空时滤波器的输出值为

y=wHx.

(3)

各阵元接收数据的协方差矩阵可表示为R=E[xxH](MN×MN维)，由线性约束最小方差准则，该处理器可以描述为如式(4)的最优化问题

(4)

在约束条件下求得权向量的第一阵元的加权系数w11=w12=…=w1N=1，利用拉格朗日乘子法可以推导出最优空时处理器的解为

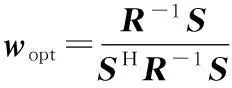
(5)

为了避免求逆过程带来运算量大的问题，首先预设一个初值w(0)，使得w从w(0)开始沿着pout减小的方向自适应的调整到wopt。pout减小的最快方向是其负梯度方向，结合约束条件wHS=1，可以得到递推式:

(6)

式中：μ为步长因子；▽pout为输出功率梯度，调整a为了满足wH(n+1)S=1成立，因此

[w(n)-μ▽wpout+aS]TS=1，

(7)

(8)

将式(8)带入式(6)可以得到递推表达式为

(9)

结合最小均方误差(LMS)算法则有

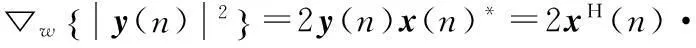
w(n)x(n).

(10)

最后可以得到基于线性约束最小方差LCMV准则的最优权值递推表达式

(11)

公式(11)中只有一个参数μ，必须选择合适的μ否则算法的收敛性不能得到保证。下面对其收敛特性进行分析。

2LCMV收敛性分析

衡量LCMV算法性能指标主要有算法的收敛性，收敛速度和稳态误差[11-12]。首先分析收敛性，它是实现其自适应功能的根本保证。定义权值误差矢量

v(n)=w0-w(n).

(12)

将式(12)代入权值更新公式，取期望利用归纳递推可得

E{v(n+1)}=(I-μR)E{v(n)}.

(13)

对R进行特征值分解R=QΛQT，并令v′(n)=QTv(n)，则式(13)可变换为

E{v′(n+1)}=(I-2μΛ)nE{v′(0)}.

(14)

当n→∞，I-2μΛ→0，此时权系数的期望值才能收敛到最优权矢量。因此要使LCMV算法收敛于均值，必须使步长因子μ满足

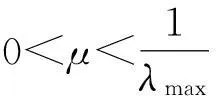
(15)

式中：λmax是协方差矩阵R的最大特征值，当迭代次数接近于无穷大时，自适应滤波器系数矢量近似等于最佳维纳解wopt。由于协方差矩阵是正定性Hermite矩阵，因此

(16)

式中：tr[R]为R的迹，等于R的对角线元素之和，也等于输入信号的总功率。

因此将(16)代入(15)，可以把收敛条件进一步严格为式(17)。因此如果阵元数固定，已知输入信号功率和滤波器阶数，通过式(17)选择合适的步长因子，可以控制自适应算法的收敛性。

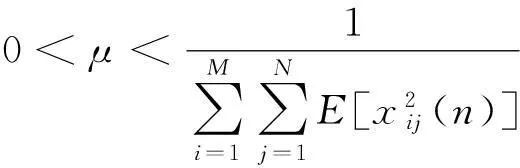
(17)

其次分析算法的收敛速度，需要引入时间常数参数。当步长参数μ比较小时，时间常数近似为

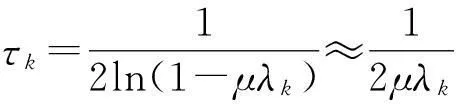
(18)

由式(18)可知，时间常数与迭代步长μ成反比，步长μ越小，算法收敛速率越慢，步长μ越大，算法收敛速率越快。如图2所示，不同的μ收敛速度不同，μ=0.005时，迭代次数在500点之后才开始收敛，而μ=0.01时，迭代次数在200点之后就收敛了。

图2　不同步长参数的输出收敛曲线图Fig.2　Convergence diagram of different step size parameters

为了进一步分析衡量算法收敛速度的指标，定义最大时间常数为

(19)

当输入信号相同时，最大时间常数下界可写为

(20)

由式(20)可以看出，最快收敛速度的大小由输入信号协方差矩阵R特征值的分散程度决定。而协方差矩阵R的特征值在一定程度上可以反映干扰的强度和个数，因此当没有干扰时，R特征值的分散度最小，收敛最快；当存在干扰时，如果输入阵列的信号功率谱密度具有很大的动态时，就会难以收敛。

最后分析稳态误差。在图2中，当曲线趋于稳定时，纵轴所对应的数值就是该自适应算法的稳态失调。假设没有噪声，那么在自适应迭代过程中，LCMV算法的滤波器权系数矢量就会收敛于一个稳态解，这个解为均方误差性能曲线表面的最小点，此时式(12)中的v的协方差为0，均方误差等于ξmin。然而实际过程中因为存在噪声，会引起稳态权矢量解随机地围绕最小点发生变化，产生超量均方误差，即ξ的稳态值将会大于ξmin。定义超量均方误差，反映真实性能与最佳性能在时间平均上差别的量度[13]：

EMSE=E[ξn-ξmin]≈μξmintr[R].

(21)

稳态失调定义为超量均方误差与最小均方误差的比值，它是自适应算法实际性能和最佳性能在时间平均上的差别的一个量度，表达式如下：

(22)

式(22)表现了梯度估值噪声引起的自适应系统的性能与最佳维纳解性能之间的差异。可以看出失调M正比于步长μ。因此μ是一个控制收敛速度和稳态误差的常量[14]：选择大的μ可以很快收敛，但是当收敛到wopt附近后将在一个较大的邻域内抖动而无法进一步收敛；选择较小的步长可以收敛到wopt附近很小的邻域，但是收敛速度非常缓慢。

3归一化变步长LCMV算法

比较归一化LCMV算法的递归表达式与传统的LCMV算法的递归表达式，可以看出归一化LCMV算法可以看作是一种特殊的变步长的LCMV算法，通过除以信号功率进而消除由于输入权向量过大而导致的噪声增加。同时，也增大了算法的动态输入范围，提高算法的收敛速度，因此比传统的LCMV算法收敛性能更佳。

xH(n)w(n).

(24)

如图3所示，归一化LCMV算法在1 000次迭代后收敛到最小均方误差，而LCMV算法在5 000次迭代后才收敛到最小均方误差。可见，由于变步长的原因使得归一化LCMV算法具有更快的收敛速度，另外归一化LCMV算法的收敛条件与输入信号的特征值无关，并且计算量与LCMV算法相当，因此归一化LCMV算法在实际中比LCMV算法应用更为广泛。

图3　归一化LCMV和LCMV的稳态误差输出值比较Fig.3　Comparison diagram of static error between normalized LCMV and LCMV

4性能仿真

本仿真实验采用四元圆形天线阵，每个阵元的延迟数为N=3。接收机处理带宽为B=4 MBZ，中频f=46 MBZ，采样率fs=62 MBZ。噪声功率设置为-80 dBW。干扰设置情况如表1所示。

表1　干扰参数表

为了更好的反映干扰在空间中的位置信息，如图4所示，x轴为俯仰角，y轴为方位角，通过music算法得到5个干扰的空间谱峰图，与表1给出的干扰信息一致。通过采用归一化变步长LCMV自适应抗干扰算法得到自适应的权系数，利用该权系数得到抗干扰零陷图，如图5所示，零陷深度基本都在-70 dB以下，说明能够对抗该场景下的多个宽带干扰。

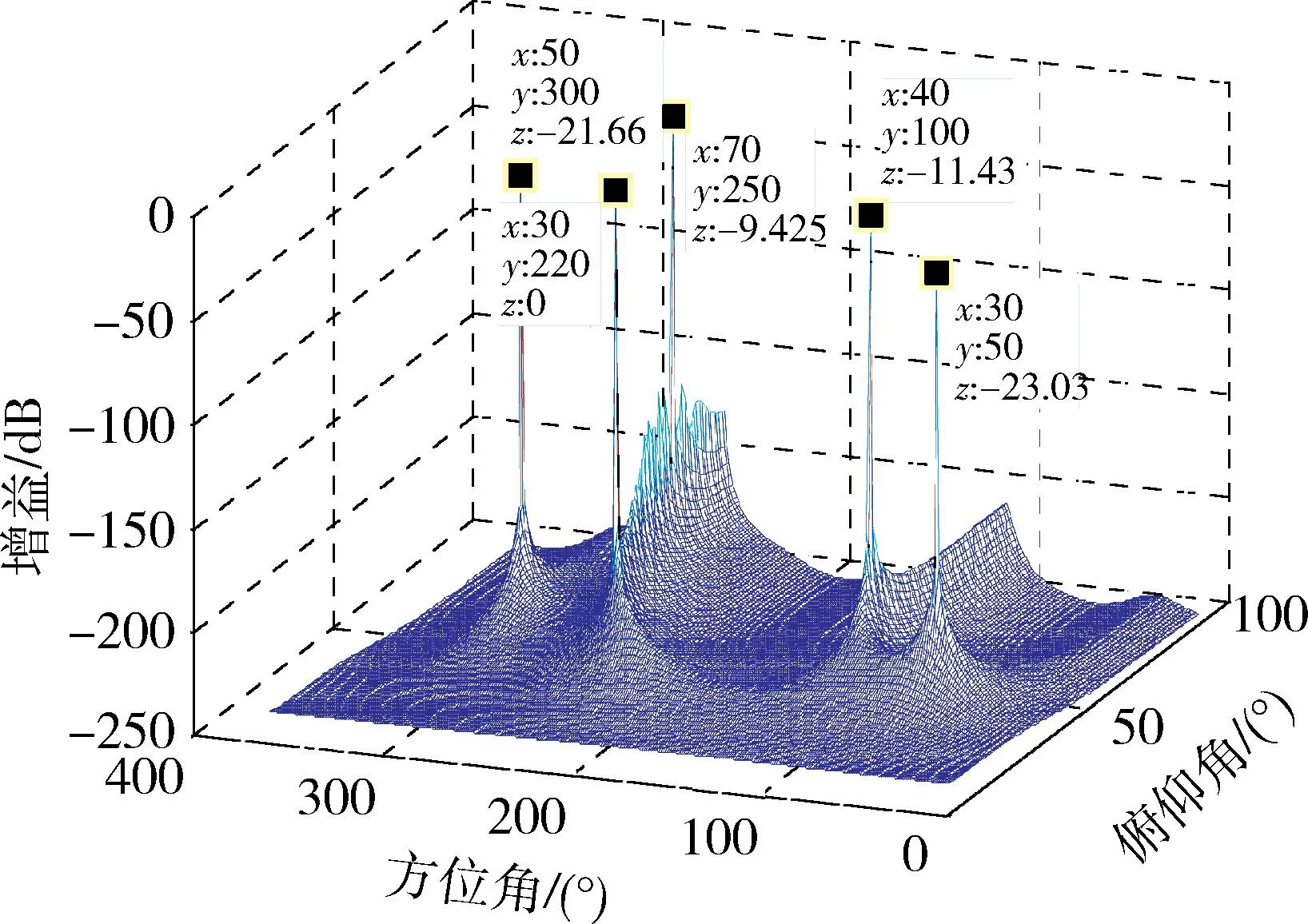
图4　干扰分布图Fig.4　Distribution diagram of interferences

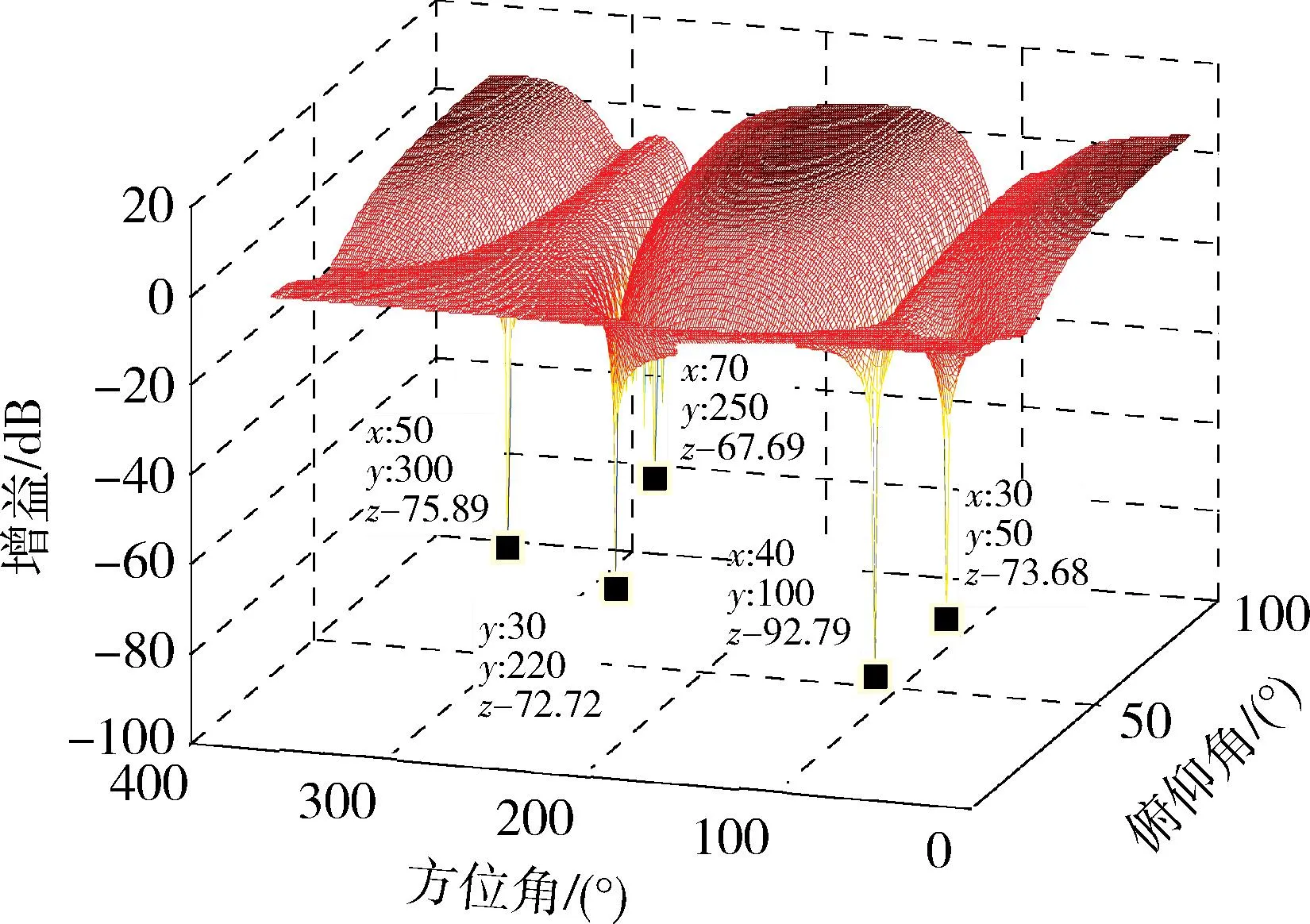
图5　自适应抗干扰零陷图Fig.5　Null steering diagram of adaptive antijamming

图6为自适应抗干扰处理收敛图，可以看出，当迭代运算在8 000点以后权值收敛，收敛时间大约为120 μs，收敛速度很快。图7为抗干扰处理前后频谱对比图，红色为抗干扰前5个宽带干扰在4 MBZ频谱内的叠加，蓝色为抗干扰后输出的噪声谱，说明自适应算法能很好地抑制干扰信号到噪声门限以下。

图6　自适应抗干扰处理收敛图Fig.6　Convergence diagram of adaptive antijamming

图7　自适应抗干扰处理前后频谱图Fig.7　Frequency spectrum diagram of adaptive antijamming

5结束语

归一化变步长LCMV算法解决了定步长算法的收敛速度和稳态误差不能同时满足的问题，该算法应用于阵列天线抗干扰方向，能很好的解决空时自适应滤波协方差矩阵求逆运算量大的问题，通过迭代运算可以达到和求逆运算一样的抗干扰效果，便于工程实现。经实验仿真表明，对大于阵元个数的多个宽带干扰，算法收敛快速，能在干扰方向上形成很深零陷，将干扰抑制到噪声门限以下。

参考文献：

[1]王永良，丁前军，李荣锋.自适应阵列处理[M].北京：清华大学出版社，2009：73-80.

WANG Yong-liang, DING Qian-jun, LI Rong-feng. Adaptive Array Processing[M].Beijing : Tsinghua University Press,2009:73-80.

[2]Li Jow Hsin. Study of Adaptive Antenna Array for GPS Interference Mitigation[D].Master’s thesis, National Cheng Kung University，2005.

[3]郭艺.GPS接收机空时抗干扰理论与实现关键技术研究[D].长沙：国防科学技术大学，2007.

GUO Yi. The Theory and Key Realization Technologies of Space-Time Interference Suppression for GPS Receiver[D].Changsha: National University of Defense Technology,2007.

[4]FANTE R L, VACCRO J J. Wideband Cancellation of Interference in a GPS Receive Array[J]. IEEE Trans on AES,2000,36(2):549-564.

[5]REED C W, VAN WECHEL R, JOHNSTON I, et al. FaSTAPTM: A Scalable Anti-Jam Architecture for GPS[C]∥ Position Location and Navigation Symposium, 2004:496-502.

[6]张全普，邱丽原. LMS自适应滤波器干扰方法[J]. 电子科技，2012，25(7):86-88.

ZHANG Quan-pu, QIU Li-yuan. Research on Jamming Methods Against the LMS Adaptive Filter[J]. Electronic Sci.&Tech.,2012,25(7):86-88.

[7]徐绍档，唐世军.一种变步长LMS自适应滤波算法研究[J].测试技术学报，2004,18(zl):81-84.

XU Shao-dang, TANG Shi-jun. Study of A Variable Step Size LMS Adaptive Filtering Algorithm[J].Journal of Test and Measurement Technology, 2004,18(zl),81-84.

[8]CIOFFI J M, KAILATH T. Windowed Fast Transversal Filters for Recursive Least Squares Adaptive Filtering[J]. IEEE Trans. on ASSP，1985,33(3):607-625.

[9]宋文武. GPS接收机空时抗干扰滤波技术研究[J]. 舰船科学技术，2010，32(7)：77-80.

SONG Wen-wu. Research on Space Time Anti-Jam Filtering Technology for GPS Receiver[J].Ship Sci.&Tech.,2010,32(7):77-80.

[10]孙晓昶，黄甫堪，陈强，等.GPS接收机抗干扰空时自适应滤波方法[J].系统工程与电子技术，2004，25(8):168-173.

SUN Xiao-chang, HUANG Fu-kan, CHEN Qiang, et al. Joint Space-Time Adaptive Filtering for GPS Anti-Jamming Receiver[J]. Journal of China Institute of Communications, 2004,25(8):168-173.

[11]BILCU R C, KUOSMANEN P，EGIAZARIAN K. A Transform Domain LMS Adaptive Filter with Variable Step-Size[J]. IEEE Signal Processing Letters，2002,9(2):51-53.

[12]CHAN S C, ZHOU Y. Improved Generalized-Proportionate Step Size LMS Algorithms and Performance Analysis[C]∥ ISCAS, 2006:2325-2328.

[13]POOR H V. An Introduction to Signal Detection and Estimation [M]. 2nd ed.New York: Springer-Verlag,1994.

[14]谷源涛，唐昆.新的变步长归一化最小均方算法[J].清华大学学报:自然科学版，2002,42(1):15-18.

GU Yuan-tao, TANG Kun. Novel Variable Step Size NLMS Algorithm[J]. Tsinghua Univ:Sci&Teched,2002,42(1):15-18.

[15]DOUGLAS S C, Analysis and Implementation of the Max-NLMS Adaptive Filter[C]∥The 29th Asilomar Conference on Signals, Systems and Computers, vol.1, Pacific Grove, CA,1995:659-663.

Normalized Variable Step Size Adaptive Interference Suppression on Array Antenna

YUAN Xin, WU Rong-gang, SUN Wu, JIANG Qing-fu

(Beijing Institute of Remote Sensing Equipment, Beijing 100854,China)

Abstract:Aimed at the adaptive interference suppression method on array antenna, the method and convergence of linearly constrained minimum variance (LCMV) is discussed. A normalized variable step size adaptive algorithm based on LCMV is proposed. This algorithm not only can resolve the contradiction between convergent speed and static error but also reduce the computational burden of covariance matrix inverse algorithm. It can decrease the computational amount and be realized easily. Both simulation and testing results demonstrate that the algorithm can provide faster convergence, generate deeper null steering in the direction of interferences and effectively suppress them.

Key words:adaptive； array antenna; convergent speed; static error; linearly constrained minimum variance(LCMV); antijamming

*收稿日期：2015-04-16；修回日期：2015-07-08

基金项目：有

作者简介：袁鑫(1986-)，女，陕西宝鸡人。工程师，硕士，主要研究方向为北斗导航和阵列抗干扰技术。

通信地址：100854北京市142信箱205分箱1号转十一室E-mail：yx.tiger@163.com

doi:10.3969/j.issn.1009-086x.2016.02.012

中图分类号：TN82；TN973.3；TP301.6

文献标志码：A

文章编号：1009-086X(2016)-02-0074-06

导航、制导与控制