公路高陡边坡稳定性模糊评判

陈　强， 王　东, 彭艾鑫， 周　群

(1. 四川省交通运输厅公路规划勘察设计研究院，四川成都 610041； 2. 上海大学土木工程系，上海 200072)



公路高陡边坡稳定性模糊评判

陈强1， 王东1, 彭艾鑫2， 周群2

(1. 四川省交通运输厅公路规划勘察设计研究院，四川成都 610041； 2. 上海大学土木工程系，上海 200072)

【摘要】在分析影响雅康路高陡边坡稳定性因素的基础上，确定了高陡边坡稳定性评价指标，运用模糊数学综合评判方法建立了高陡边坡稳定性评价的模糊层次分析模型，对边坡的稳定性进行了综合评判，并采用Matlab程序编制了高陡边坡稳定性快速分级系统，实现边坡稳定性判定的可视化。实例表明，模糊理论评价结果较真实的反映了边坡所处的稳定状态，评判程序简便可行，实现了高陡边坡稳定性的快速评判。

【关键词】高陡边坡；评价指标；Matlab程序；模糊评判；稳定性

确保边坡的稳定性具有十分重要的工程意义，一直是岩土工程界研究的热门课题[1-2]。边坡的稳定性目前常采用极限平衡法、可靠度理论评价法、有限元法、灰色聚类评价法、神经网络评价法等方法进行分析，鉴于影响边坡稳定性的影响因素[3-5]较多,导致所建立的平衡方程不是十分精确或者算法过于复杂，可操作性不强。因此，根据具体的边坡地质条件，合理选取边坡的评价指标和相适应的评价方法快速评判边坡的稳定性是值得深思的问题。

本文在对四川雅康路线两边边坡进行调研分析的基础上，对影响边坡稳定性的地质条件、地形地貌特征以及其他因素进行了综合分析，将层次分析法和模糊数学方法结合起来建立了高陡边坡稳定性模糊层次分析模型，并采用Matlab程序进行编程，建立高陡边坡稳定性评价图形用户界面，实现高陡边坡稳定性判定的快速化、可视化。

1建立高陡边坡稳定性模糊综合层次评判模型

1.1构建高陡边坡稳定性评价指标体系

遵照构建边坡稳定性评价指标体系的可操作性、层次性和系统性的原则，在查阅国家行业规范和大量文献的基础上进行综合分析，影响边坡稳定性的影响因素较多，在已有研究成果[6-9]的基础上，结合雅康高速公路高陡边坡的特点，确定出分析高速公路高陡边坡稳定性的主要因素为A1地形地貌、A2工程地质因素、A3气象水文地质因素和A4其他因素的4个一级指标。其中，地形地貌又包括B1自然坡高、B2自然坡角、B3坡面形态、B4植被覆盖率4个二级指标；工程地质因素包括B5岩体结构类型、B6岩体风化程度、B7结构面发育程度、B8岩性及岩性组合4个二级指标；气象水文地质因素包括B9多年平均降雨量、B10岩层透水性(渗透系数)、B11地下水、B12降雨的冲刷作用4个二级指标；其他因素包括B13开挖方式和B14地震烈度2个二级指标。根据研究指标建立的高陡边坡稳定性模糊层次评价体系如图1所示。

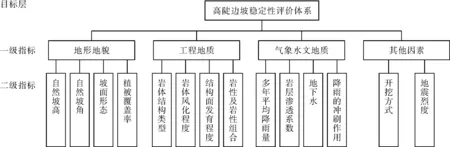
图1　高陡边坡稳定性层次评价体系

1.2确定评价指标的权重

判断矩阵是将各层次的因子与上一级的评价指标的相对重要性进行两两比较，确定各因子之间的相对优越度，构建各自的判断矩阵M。采用1～9度的量化标度来反应同一层次评价指标的相对重要性(表1)。评价指标之间的相对重要性对模糊综合评价结果有重要的影响，必须按照评价指标的重要性及他们对稳定性的影响程度进行客观的评价。

确定评价指标的权重需要计算每一个判断矩阵的权向量，进而组成判断整个判断矩阵的权向量，从而为科学评判高陡边坡的稳定性提供依据。对于任意一个判断矩阵M，首先要算出该矩阵的最大特征值λmax，进而求出矩阵的特征向量W，即MW=λmaxW，对W进行归一化，满足∑Wi=1，此时W中的各个分量即为对应评价指标的相应权重。

表1　标度值的含义与重要等级

注：(2，4，6，8)表示重要性介于上述标度中值

确定评价指标的权重步骤如下：

(1)根据表1中的量化标度对各层次的指标评判权重，构建判断矩阵M。

(2)计算矩阵M的最大特征值λmax和特征向量W。

①计算判断矩阵Mi每行评价指标的几何平均，即Mi的各指标按行相乘并开n次方：

(1)

②将Wi进行归一化为权重向量Wi：

(2)

③计算判断矩阵M最大特征值λmax：

(3)

(3) 一致性检验。

当判断矩阵的评价指标较多时，构造出的判断矩阵可能有悖常理，需要进行一致性检验：

(4)

式中：CI为一致性指标；RI为平均随机一致性指标。若n<3时，矩阵具有完全一致性，CI=0；若n≥3时，RI可根据表2按照矩阵的阶数查取。若一致性指标CR=0，则表示判断完全一致，一般只要满足CR<0.1即可(表2)。

表2　平均一致性指标RI

据此，可得出高陡边坡稳定性评价的一级指标A和二级指标B的各评价指标的相对权重计算结果(表3)。

1.3评价指标隶属度的确定

隶属度是用来描述各评价指标与评价所属等级之间的模糊关系。根据影响边坡稳定性的各评价指标的特点，将评价指标分为定性和定量两类，前者属于离散型变量，后者属于连续型变量。根据隶属度建立的原则，在对本次边坡稳定性评价过程中，针对评价指标(表4)的不同类型，分别采用了专家评定法和公式法两种方式建立相应评价指标的隶属度[10]。

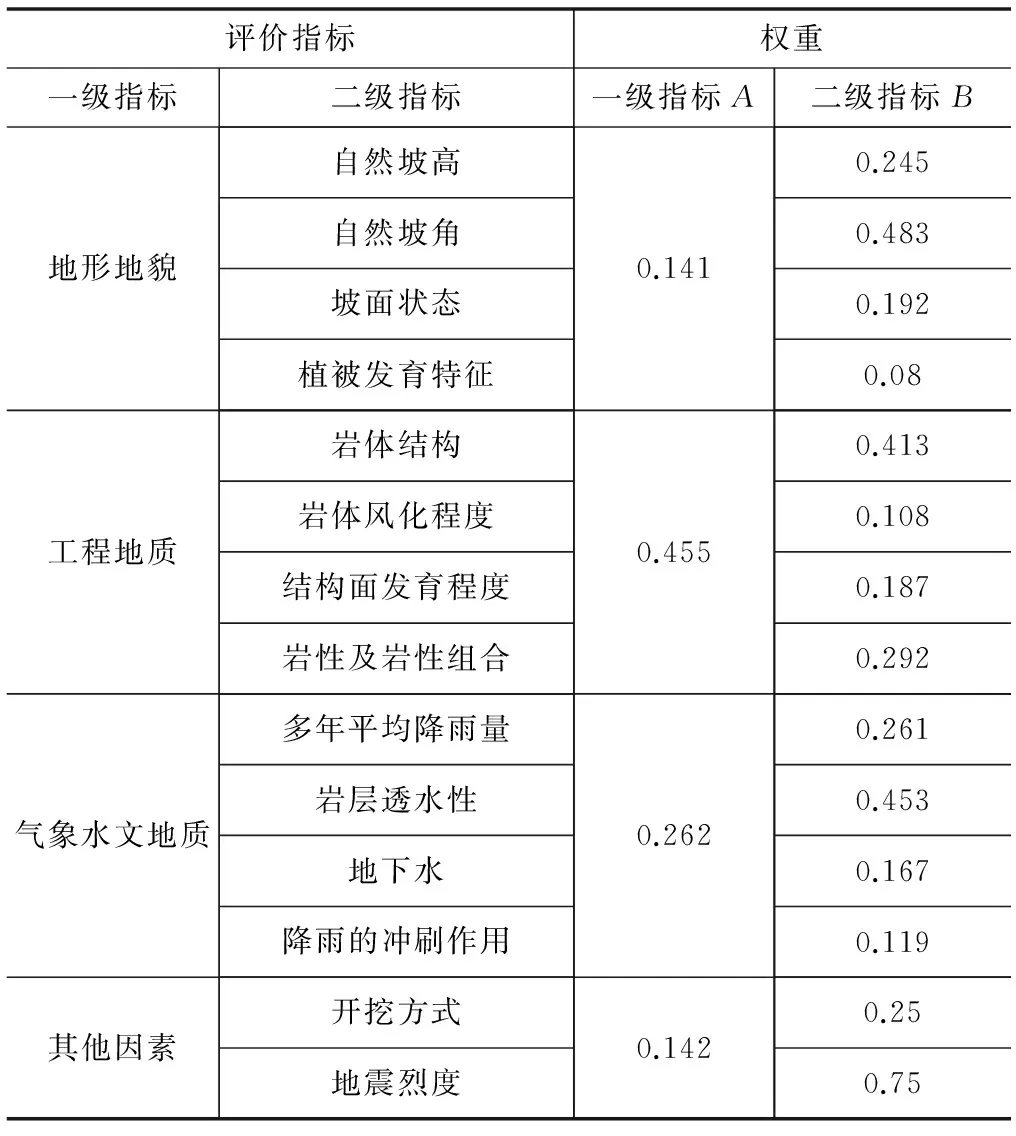
表3　高陡边坡各评价指标权重

1.3.1离散型指标隶属度

对表4中坡面形态、植被覆盖率、岩体结构类型、岩性及岩性组合、地下水、开挖方式6个离散型指标，根据国内类似研究[11]，其隶属度采用专家评定法确定，其值见表5。

1.3.2连续型指标隶属度

对表4中的自然坡高、自然坡角、岩体风化程度、结构面发育程度、多年平均降雨量、岩层渗透系数、降雨的冲刷作用、地震烈度等连续性指标采用公式法确定其隶属度。用于确定隶属度与指标取值之间的函数关系，即为隶属函数。隶属函数种类很多，本文综合各指标数据的分布特征，采用“降半梯形”分布描述连续性指标的隶属函数，计算公式如下：

(5)

(6)

(7)

(8)

(9)

式中： S1～S5分别为边坡稳定性分级的5级标准值；x为边坡评价指标的实测值。

1.4确立指标评判集

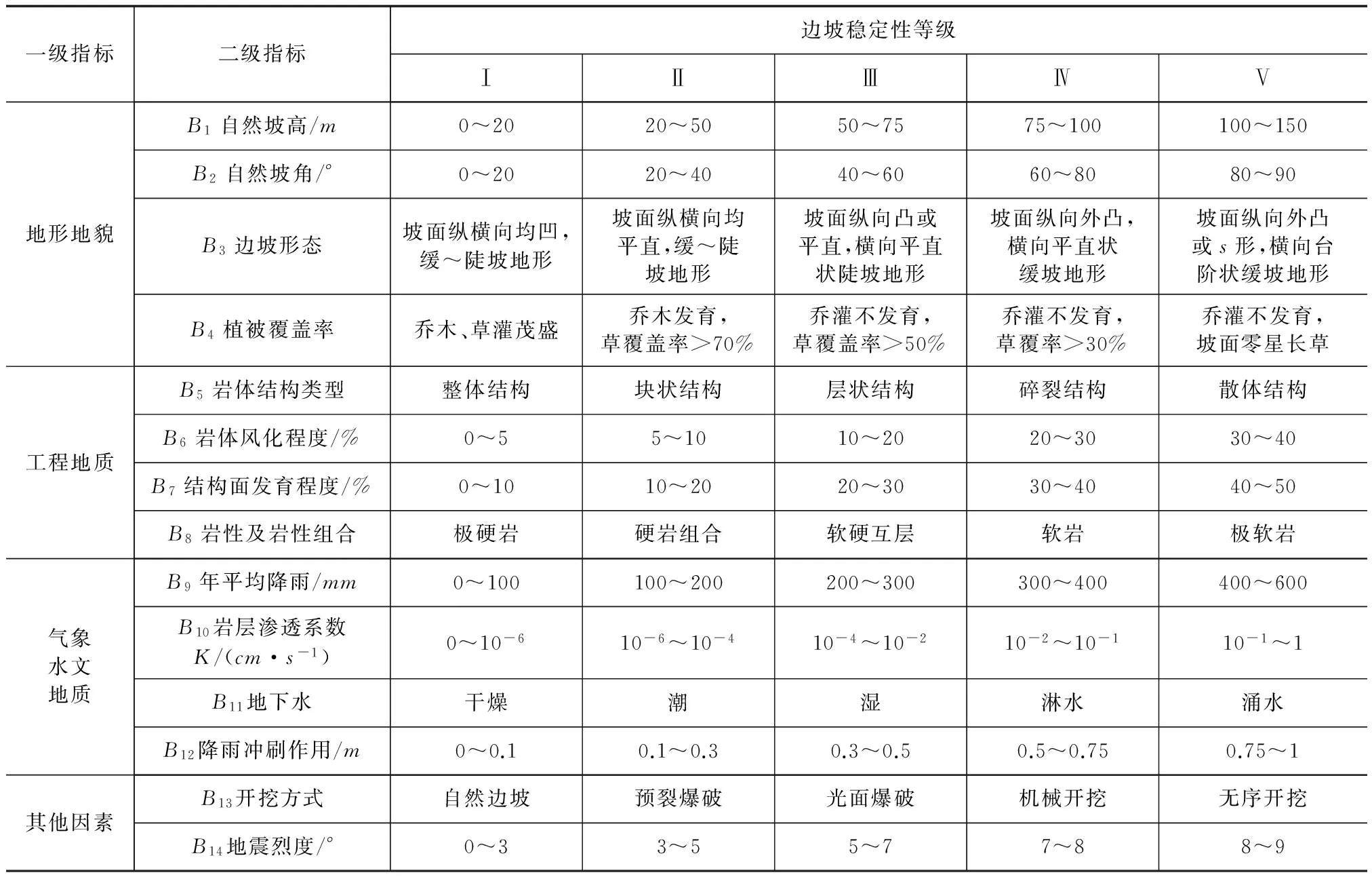
结合雅康高速公路高陡边坡的特点，考虑相关资料收集的方便和易操作性，参照相关规范分类标准[12]，将高陡边坡的稳定性分为5个等级，即稳定(Ⅰ级)、基本稳定(Ⅱ级)、局部稳定性差(Ⅲ级)、不稳定(Ⅳ级)、极不稳定(Ⅴ级)。具体的分级标准如表6所示，对于不同的边坡稳定状态提供了相应的防控对策。

1.5高陡边坡模糊层次综合评判

对高陡边坡建立的模糊层次评判模型首先应对二级指标进行评判，然后将评判结果作为新的评判因素构成评判矩阵，进行模糊层次总评判。

(1)根据评价指标选取合理的隶属函数，采用隶属函数对二级指标进行量化处理，进而求得二级指标的隶属度，将二级指标的计算结果进行组合得到各单因素的评判矩阵Ri：

(10)

其中：n表示研究对象各指标取评价集中第n个等级的可能性；m表示研究对象的第m个因素所对应评判矩阵各等级的隶属度。

(2)由二级指标权重向量Bi和单因素的评判矩阵Ri确定一级模糊评判矩阵Ci:

(11)

式中：i=1,2,3,4,5；模糊算子°选择为M(·，+)，考虑各评判指标所起的作用。

(3)将一级指标权重向量A和一级模糊评判矩阵Ci得到二级模糊综合评判向量B:

(12)

1.6评价指标的处理

将向量B中各具体的值乘以模糊综合评价结果对应的评价等级，加权平均得到一个点值。则模糊综合评价向量可单值化为:

(13)

式中：F为加权平均数；n为评价集中向量的个数；Bi为评价集中的向量；Mi为评价等级所属的值；K为待定系数

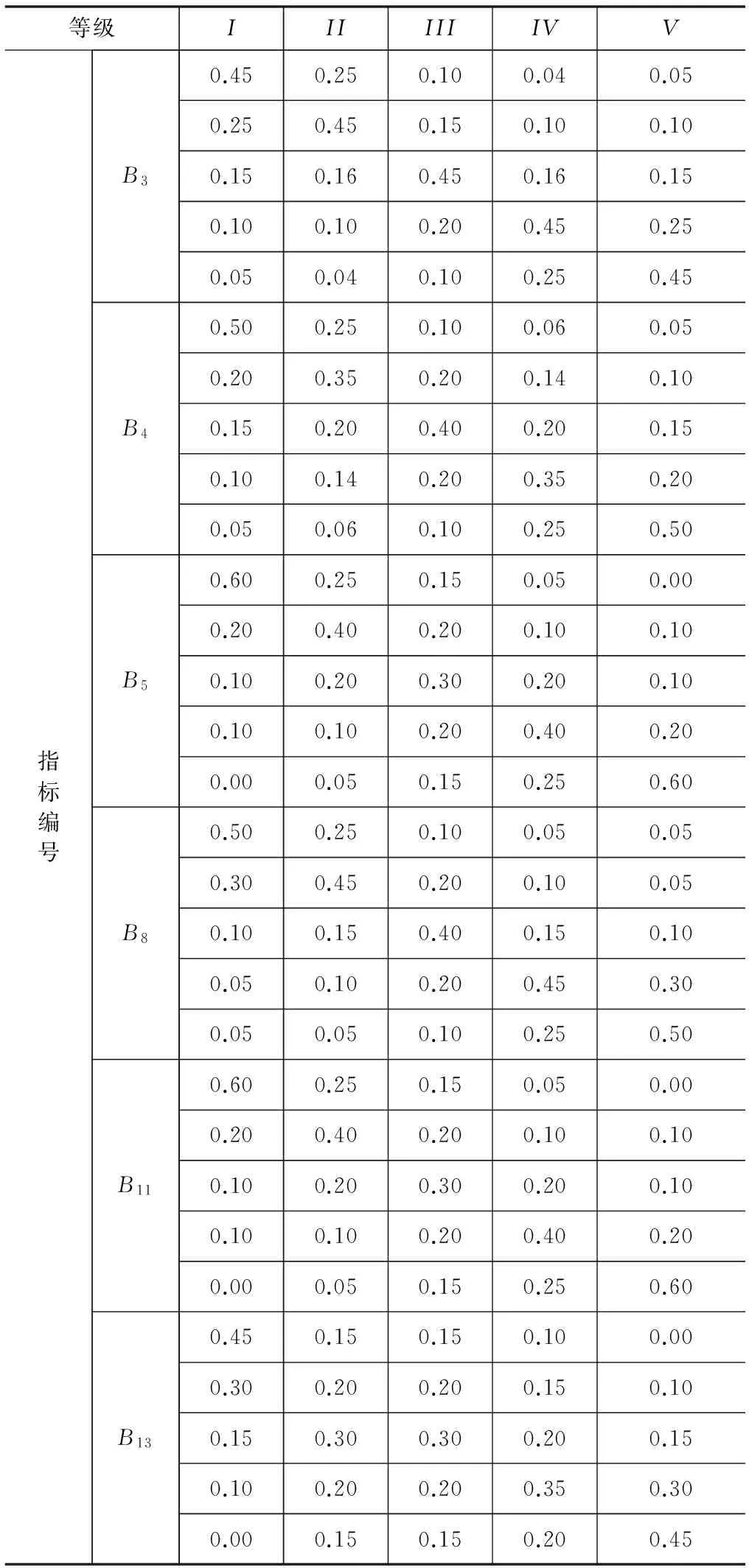
表5　离散型指标隶属度取值

表6　高陡边坡稳定性分级标准

(一般取1或2)。

高陡边坡模糊层次综合评判的安全等级量化见表7。

2建立高陡边坡稳定性快速分级系统

采用MATLAB程序依据高陡边坡稳定性判断层次分析理论进行GUI编程设计，包括对象的回调函数、程序的一般结构、对象属性的访问、对象间数据传递、GUI与M文件的数据交互以及GUI与Simulink仿真的数据交互等，编成图形用户界面，界面菜单包括文件、设置、结果、帮助和退出5个部分，以便更好地进行人机交互，建立高陡边坡稳定性评价运行界面，实现高陡边坡稳定性判定的可视化(图2)。

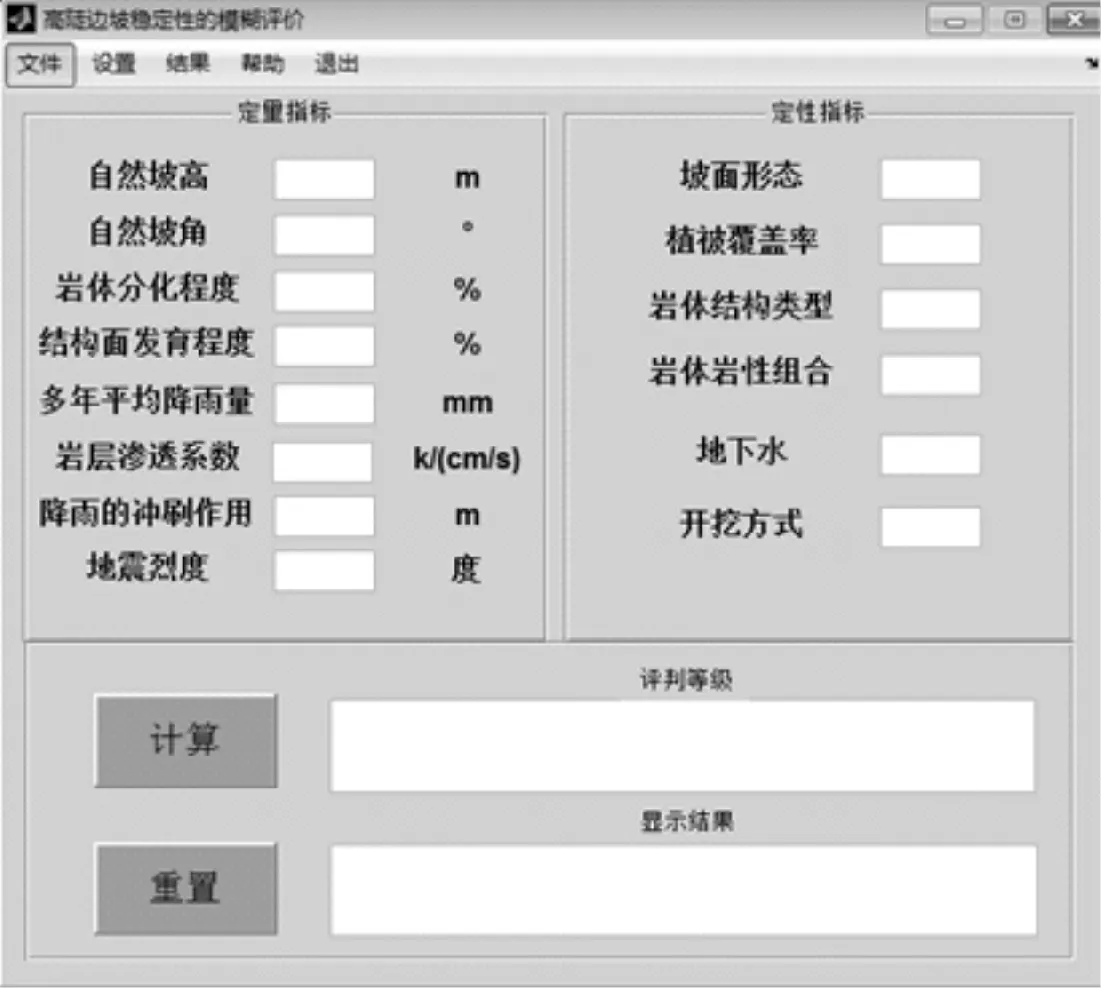
图2　高陡边坡稳定性评价运行界面

3工程应用

雅康高速沿线位于四川盆地与青藏高原过渡地带，起点雅安市海拔高约580m，终点康定县城海拔达2 500m。该地区属于亚热带湿润季风气候，地形地质条件复杂，坡体植被形态发育，多年平均相对湿度66 %，平均降雨量642.9mm。

咱里桥位左岸为顺直斜坡，下部为早期崩坡积形成的台地，上部横坡35°～40°，横坡高约450m，顺直陡坡(坡面形态为III级)，覆盖层为崩坡积块碎石土，厚15～33m，稍密-中密，强风化约2～10m(15 %)，岩体块状结构，致密坚硬(II级)，边坡中主要发育5组节理(12 %)，将边坡岩体切割成镶嵌块状结构，边坡植被较为发育(III级)。经调查研究，其他相关资料如下：地下水主要赋存于岩石构造裂隙中，渗透系数0.012m/d，属弱富水岩组，降雨冲刷作用较强(0.6m)。土体工程地质类型为冲积、冰水沉积松散工程地质岩组，岩体工程地质类型为极硬-次硬块状机性岩组(I级)，开挖方式采用光面爆破，地震基本烈度Ⅶ度。

采用上述层次模糊综合评价方法对上述边坡进行稳定性评价，根据工程实际情况边坡的综合评价结果见表8。

表8　边坡的评价指标特征值

3.1相对隶属度计算

根据上述条件，求的地形地貌等四个二级指标的相对隶属度向量：

C1=B1°R1=(0.148,0.407,0.118,0.054,0.273)

C2=B2°R2=(0.399,0.344,0.166,0.056,0.035)

C3=B3°R3=(0.403,0.075,0.104,0.122,0.303)

C4=B4°R4=(0.037,0.050,0.825,0.050,0.037)

3.2模糊综合评判

对高陡边坡稳定性分级有较大影响的地形地貌、工程地质因素、气象水文因素、其他因素4个分类指标进行重要性排序，用层次分析法计算其权重(表3)，故其权向量为：

A=(0.141，0.455,0.262,0.142)

由此可计算综合评价隶属度向量B:

B=A°Ci=(0.313，0.240，0.235，0.072，0.140)

咱里桥左侧边坡稳定性安全评价值为:

由评价结果可知该边坡的稳定性分级为第二级，边坡处于基本稳定状态，该结果与项目工程初期勘测报告较为吻合，表明该方法能够较好地用来对高陡边坡进行稳定性评价。

4结论

结合层次分析法和模糊综合评判方法构建了高陡边坡二级模糊层次综合评判模型，通过对实际高陡边坡模糊层次综合评判，得出如下结论：

(1)模糊层次综合评判方法通过建立综合评判指标体系，对高陡边坡进行多因素、多层次的综合评判，比较全面的考虑了影响高陡边坡稳定性的各个因素。

(2)运用模糊层次综合评判方法进行高陡边坡综合评价，所得的评价结果不仅可以直观的反应边坡的稳定状态，而且可以得到各种影响因素的综合评判值。这种方法得到的结果信息量更大，更有说服力。

(3)基于Matlab程序编制了高陡边坡稳定性的快速评价系统，实现边坡稳定性判定的可视化，评判方法直观，为边坡稳定性判断提供了有效参考。

参考文献

[1]赵尚毅, 郑颖人, 时卫民, 等. 用有限元强度折减法求边坡稳定性安全系数[J]. 岩土工程学报, 2002, 24(3): 343-346.

[2]董金玉, 杨国香, 伍法权, 等.地震作用下顺层岩质边坡动力响应和破坏模式大型振动台模型试验研究[J]. 岩土力学, 2011, 32(10): 2977-2983.

[3]温世亿, 李建林, 杨学堂, 等. 卸荷高边坡稳定性分析的多级模糊综合评判[J]. 岩土力学, 2006, 27(11): 2041-2044.

[4]夏元友, 熊海丰.边坡稳定性影响因素敏感性人工神经网络分析[J]. 岩石力学与工程学报, 2004, 23(16): 2703-2707.

[5]洪海春,徐卫亚,叶明亮,等. 基于模糊综合评判的边坡稳定性分析[J]. 河海大学学报:自然科学版, 2005, 33(5): 557-562.

[6]宋晓秋. 模糊数学原理与方法[M]. 徐州：中国矿业大学出版社，1999:201-203.

[7]黄建文, 李建林, 周宜红.基于AHP的模糊评判法在边坡稳定性评价中的应用[J]. 岩石力学与工程学报, 2007, 26(增刊): 2627-2632.

[8]黄锦林,赵吉国,张婷,等. 基于层次分析法的库岸高速滑坡危险度评价[J]. 自然灾害学报,2011, 20(5): 95-99.

[9]赵建军, 黄润秋, 向喜琼. 某水电站近坝库岸边坡稳定性二级模糊综合评判[J]. 水文地质工程地质,2004(2): 45-49.

[10]刘春, 白世伟, 王刚. 黄麦岭磷矿采场边坡稳定性模糊综合评判[J]. 矿冶工程,2002, 22(4): 21-23.

[11]张勇慧, 李红旭, 盛谦, 等. 基于模糊综合评判的公路岩质边坡稳定性分级研究[J]. 岩土力学,2010, 31(10): 3151-3156.

[12]GB50487-2008 水利水电工程地质勘察规范[S].

[基金项目]四川省交通科技项目《高烈度地震峡谷区公路松散体边坡稳定性及防治技术研究》(项目编号:2012A2-4)

[作者简介]陈强(1972～),男，博士，高级工程师，主要从事公路工程、岩土工程和地质工程等方向的研究。

[通讯作者]彭艾鑫(1989～)，男，硕士，主要从事复合材料加筋土方向研究。

【中图分类号】U416.1+4

【文献标志码】A

[定稿日期]2015-11-04