基于刚度反演的大型振动筛减振弹簧健康识别

彭利平，刘初升，王　宏

(1．河海大学机电工程学院，江苏常州　213022;2．中国矿业大学机电工程学院，江苏徐州　221116;3．中煤科工集团 唐山研究院有限公司，河北唐山　063012)



基于刚度反演的大型振动筛减振弹簧健康识别

彭利平1，刘初升2，王宏3

(1．河海大学机电工程学院，江苏常州213022;2．中国矿业大学机电工程学院，江苏徐州221116;3．中煤科工集团 唐山研究院有限公司，河北唐山063012)

摘要:针对已有的大型振动筛减振弹簧定性健康识别的局限性，提出了1种利用筛体自由振动响应实现大型振动筛减振弹簧刚度反演的方法。考虑减振系统几何位置误差，建立了减振弹簧故障下振动筛非对称动力学模型，推导其振动微分方程;利用离散加速度自由响应，结合数字滤波、趋势项消除和数值积分方法，获取系统刚度矩阵修正形式;在此基础上，通过刚度矩阵分解，定义刚度置信准则，提出了大型振动筛减振弹簧刚度反演原理与方法;利用实验测试数据实现了振动筛减振弹簧的刚度反演，最大误差仅为3．56%，表明了算法的有效性，实现了减振弹簧定量的健康状态识别。

关键词:振动筛;减振弹簧;刚度反演;健康识别

彭利平，刘初升，王宏．基于刚度反演的大型振动筛减振弹簧健康识别［J］．煤炭学报，2016，41(6):1568－1574．doi:10．13225/j．cnki．jccs．2015．1200

Peng Liping，Liu Chusheng，Wang Hong．Health identification for damping springs of large vibrating screen based on stiffness identification ［J］．Journal of China Coal Society，2016，41(6):1568－1574．doi:10．13225/j．cnki．jccs．2015．1200

选煤是实现煤炭清洁高效利用、节约资源、保护环境的有效方法。筛分作业是选煤的关键环节，目前被广泛应用的筛分设备是振动筛［1－2］。随着我国大型煤炭基地大型选煤厂、大中型煤矿配套选煤厂和小型煤矿集中矿区群矿选煤厂的建设［3］，处理量大、效率高的大型振动筛(筛面宽度不小于3.6 m、筛分面积不小于20 m2)［4］被广泛应用。传统振动筛动力学模型主要是单自由度或两自由度互不耦合振动系统，实现的前提是4点减振弹簧完全相同［5］。然而，振动筛在激振系统强交变载荷和物料随机载荷联合作用下，减振弹簧易疲劳损伤，引发动力学模型的突变，宏观上将导致筛体运动轨迹变化，影响设备可靠性及效果。

目前对振动筛减振弹簧健康监测方面的报道较少。笔者建立了适合减振弹簧故障下振动筛运动描述的三自由度动力学模型，讨论了其对传统动力学模型的向下兼容性，并基于此实现了振动筛一故障弹簧和一健康弹簧的定位［5］;在此基础上，又综合考虑筛面静平衡和筛面约束条件下的减振弹簧小位移变形协调，建立了定点压力作用下各弹簧压缩变形量的计算模型，并推导其计算表达式，通过数值仿真分析各弹簧压缩变形量与悬挂质量位置的定性关系，推导了定点压力作用下故障前后弹簧压缩量变化与弹簧刚度变化的定量关系，提出了利用变形灵敏度系数(DSC)来反映弹簧压缩量对弹簧刚度变化的灵敏程度，并基于此提出了振动筛减振弹簧故障诊断的2次悬挂质量法［6－7］。上述研究对振动筛减振弹簧健康状态的评估具有一定的有效性，但是局限于定性判断，且仅能识别一故障弹簧。若能利用大型振动筛的动力学特性反演计算减振弹簧的有效支撑刚度，并与设计值比较，就能从弹簧刚度数值上定量弹簧健康状态。

笔者先建立了减振弹簧故障下振动筛非对称动力学模型，从自由响应出发，实现了振动筛系统刚度矩阵的推导和刚度反演原理的提出，最后将所提原理在实验室振动筛模型机上进行了弹簧刚度反演的应用测试，证实了其有效性。

1　减振弹簧故障下振动筛非对称动力学模型

减振弹簧故障下筛体经历空间复杂运动，笔者给出了减振弹簧故障下的振动筛耦合动力学模型［5］，主要考虑了筛体“浮沉”、“侧滚”和“点头”运动的耦合。由于减振系统几何位置误差下4点减振弹簧支撑可能非对称分布，不失一般性，这里建立弹簧故障下振动筛非对称动力学模型［8］，如图1所示。

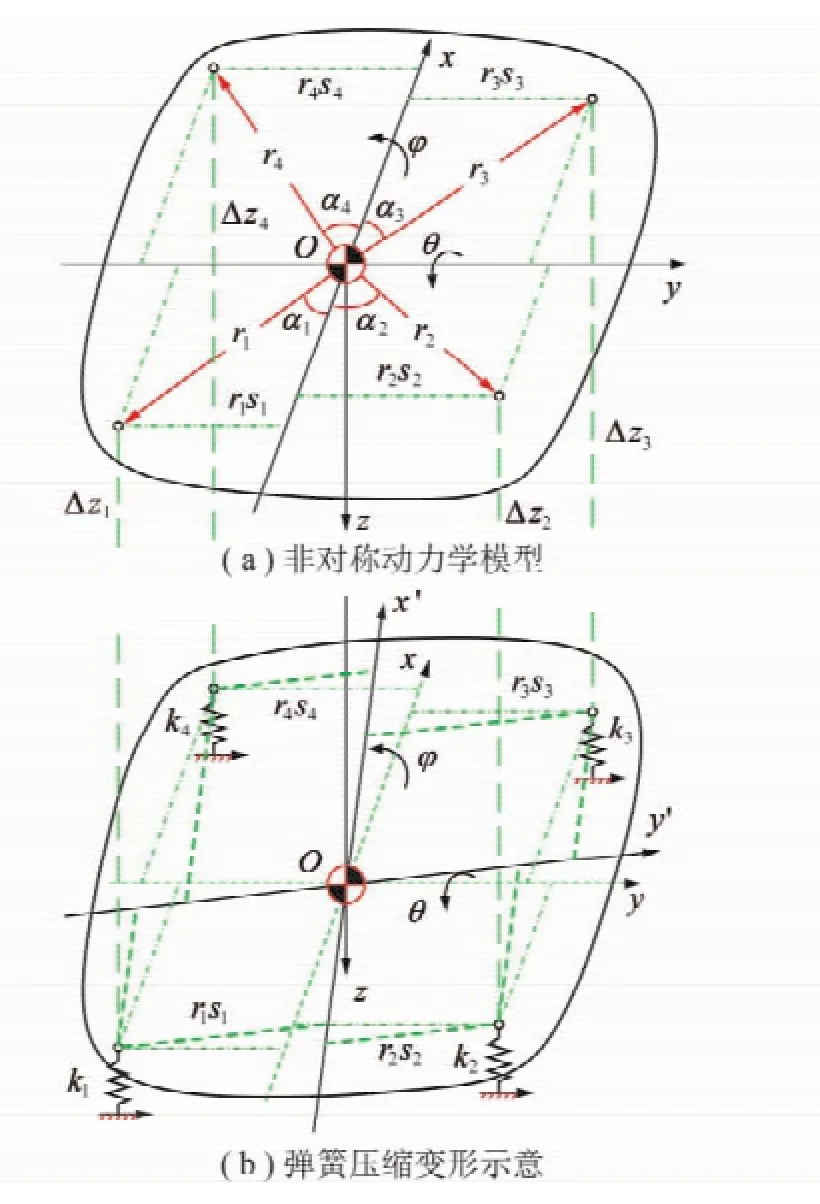
图1　减振弹簧故障下振动筛非对称动力学模型及弹簧压缩变形示意Fig.1　Asymmetric dynamic model of the vibration screen with damping spring fault and sketch for the compressed deformation of damping springs

由于筛体刚度大，激振频率一般小于筛体弹性变形的基频，因此自由振动时可忽略其弹性变形。无扰动下静平衡筛面处于图1(a)位置;当筛体振动时，某一时刻筛面处于图1(b)位置。减振弹簧各支点与质心O的位置关系以距离ri和夹角αi(i=1，2，3，4)表示。设筛体质量为m，绕x轴和y轴的转动惯量分别为Jx和Jy，任意时刻运动量以筛体竖直方向位移z、绕x轴转动角φ及绕y轴转动角θ这3个自由度(广义坐标)表示。

扰动下减振弹簧的竖直压缩变形量分别为Δz1，Δz2，Δz3和Δz4，以3个广义坐标的耦合表示为

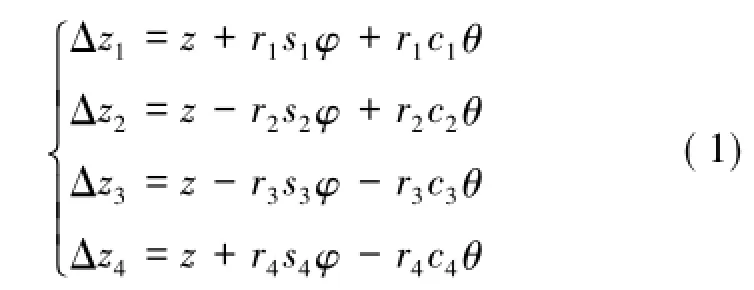
其中，si=sin αi且ci=cos αi(i=1，2，3，4)。由于刚体摆动幅度很小，将sin φ和sin θ利用零值处欧拉公式展开后可分别替代为弧度制下的φ和θ。

为方便计算，将式(1)用矩阵表示

式中，x={z，θ，φ}T为广义坐标矩阵;T为广义坐标至减振弹簧竖直压缩量的映射矩阵，

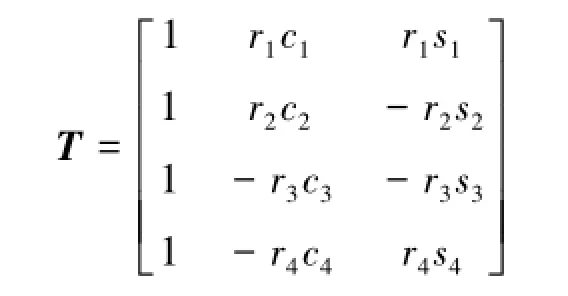
一般地，工程线性系统阻尼往往是看作比例黏性阻尼［9］。基于拉格朗日方程，减振弹簧故障下振动筛比例阻尼系统自由振动微分方程［10］一般表示成:

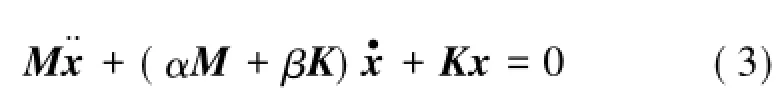
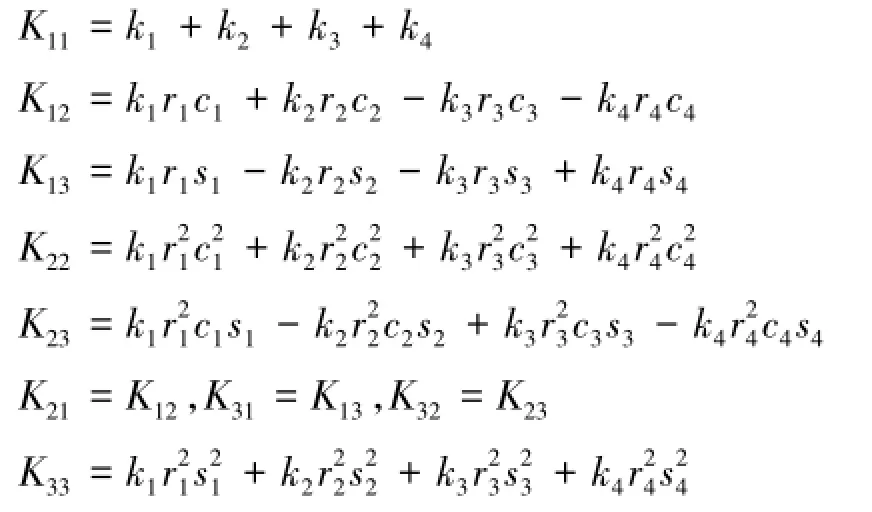
很明显，由于是线性动力系统，刚度矩阵K为对称阵，各元素为4点减振弹簧刚度表达式。

2　反演原理

2.1刚度矩阵推导

刚度反演的主要目的是通过筛体自由振动响应反推刚度矩阵中各刚度的数值，式(3)转化为

构造矩阵形式的自由振动响应，即位移X3×N= ［xk，xk+1，…，xk+i，…，xk+N－1］，其中，xk+i={x1，k+i，x2，k+i， x3，k+i}T，速度和加速度类似，其中，3为系统自由度数;N为自由振动响应中采用的离散运动量点数;k为截取起始位置;xj，k+i，和分别为第j(j=1，2，3)个自由度在第k+i个离散时刻的位移、速度及加速度。因此，式(4)可以表示成

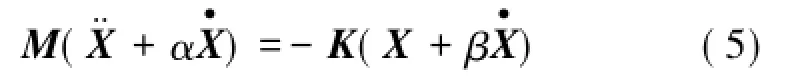
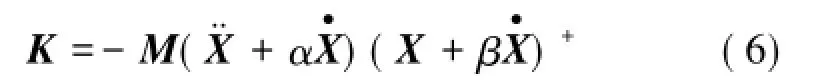
式中，上标“+”表示Moore－Penrose广义逆阵［12］。

针对图1的减振弹簧故障下振动筛非对称动力学模型，由式(2)得

构造各弹簧压缩量变形位移矩阵 ΔZ=［Δzk，Δzk+1，…，Δzk+i，…，Δzk+N－1］，其中，Δzk+i={Δz1，k+i，Δz2，k+i，Δz3，k+i，Δz4，k+i}T，而变形速度、加速度的矩阵形式依此类推。故有

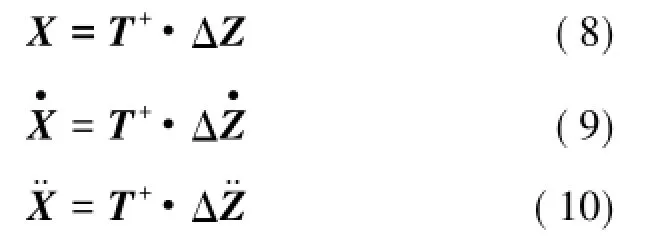
将式(8)～(10)代入式(6)中，该系统的刚度矩阵满足:

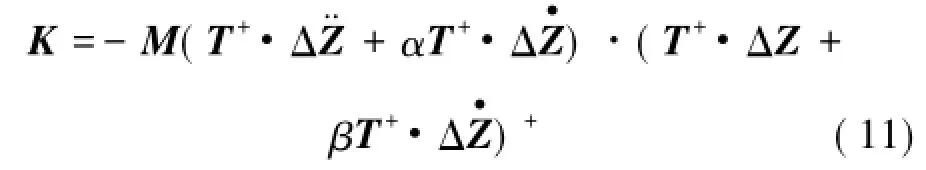
观察式(4)中各个元素，可以发现，刚度矩阵K的构型与弹簧是否存在损伤无关，因此理论上始终是对称阵。为使由自由响应矩阵和式(11)计算得到的系统刚度矩阵保持这一特性，这里引入如下数学处理［13］:

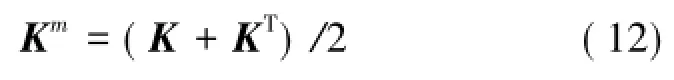
作为刚度矩阵的修正形式Km。

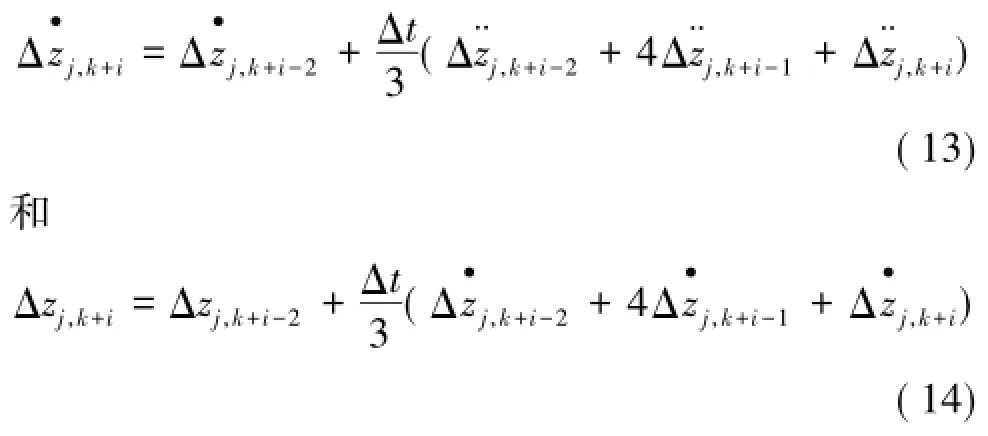
来实现速度及位移的获取，进而构造反演所需的速度及位移矩阵。其基本流程如下:

(1)鉴于实际加速度信号中的噪声干扰，利用数字滤波(DF)方法对采样的数字离散信号进行噪声剔除，保留有用成分用于构造加速度矩阵及后续数值积分的源信号;

(2)为防止源信号零漂的影响，数值积分后需进行消除趋势项(ETT)来消除直流项造成的信号偏移失真，使积分信号尽量接近真实;

(3)最后将处理后的信号构造式(6)中的自由振动响应速度及位移矩阵。

整个过程如图2所示。

图2　时域中由加速度计算速度和位移矩阵的数字信号处理Fig.2　Digital signal processing for time-zone acceleration transforming into the corresponding velocity matrix and displacement matrix

2.2反演过程与置信准则

刚度矩阵中各元素是关于各减振弹簧刚度和支点位置的函数，下面研究刚度矩阵已知的情况下进行刚度值反演识别的方法。

定义Km的刚度变形矩阵，满足［8］

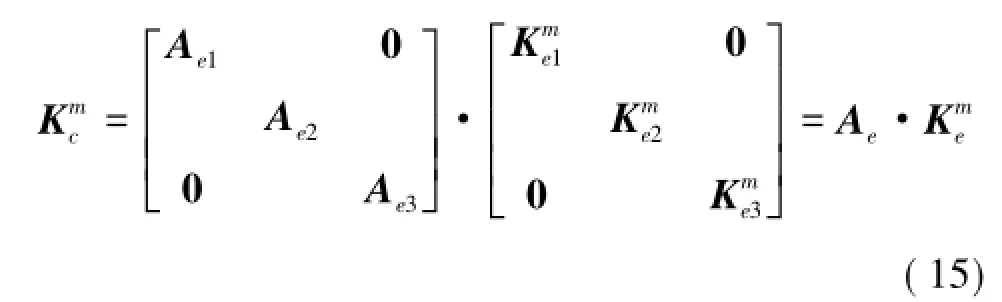
其中，Ae和Kme分别为刚度联系矩阵和单元刚度变形矩阵。刚度联系矩阵Ae只与系统弹簧支撑位置有关，弹簧刚度任意组合状态下Ae保持不变，单元刚度矩阵如下形式:

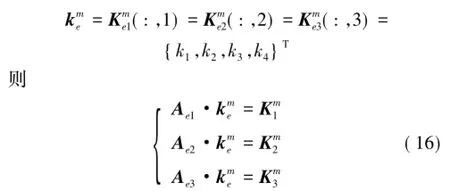
依次展开后得到的方程组中方程个数(3)均少于未知参数(4个刚度值)，为不定方程，因此方程(16)各含有无数组可行解(设为，和)。由于弹簧刚度值确定，故方程组解惟一，惟一解即公共解。采用常规的伪逆解法可分别得到各个方程组的最小范数解，但不能保证各解相同(近)而符合惟一性。为此，这里设计如下数值算法:考虑到方程组惟一解的必然存在性，使某一弹簧的刚度值在一定范围［kmin，kmax］(其中，kmin取0，kmax取弹簧刚度设计值)内进行循环赋值，以k1为例，对于任意1个数值，代入方程(16)中即可使之降维而获得惟一可行解(设为和)。为评价这些解的接近程度，类似模态置信准则MAC［14］，定义刚度置信准则:

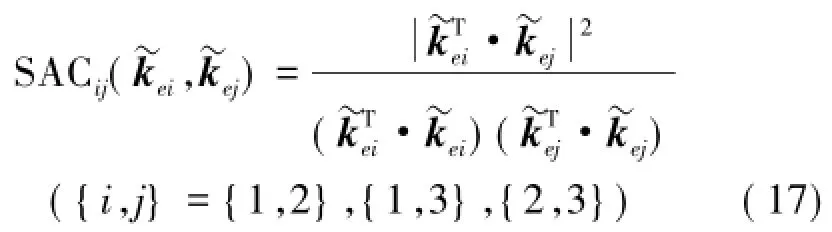
来量化两反演刚度向量的相关程度，其取值0～1。SAC值趋于 1，表明 2组反演刚度的一致性好;SAC值趋于0，说明2组反演效果不理想。

同时，定义趋向于1的刚度置信准则的阈值S，用于反映反演相关程度要求，获取所有同时满足:①SAC12()≥S，② SAC13()≥S和③SAC23()≥S的SAC值所对应的反演刚度向量。若条件①，②和③获得的反演刚度向量分别为，由于各组刚度向量间的相关程度均很高，因此可以选取6组解的平均值作为方程组(16)的公共解，其各个元素即为刚度反演值{k1，k2，k3，k4}。

3　刚度反演的实验验证

文献［8］通过数值实验，对上述刚度反演算法的准确性和有效性进行了详细的说明，其具有如下特征:反演计算所采用的信号起始位置和长度对反演精度没有影响，而只与截取信号的纯净程度相关;采用的离散运动量点数N越大，一般反演效果越好;DF中带通数字滤波截止频率由结构固有频率决定，带宽略大于固有频率的最大差值。

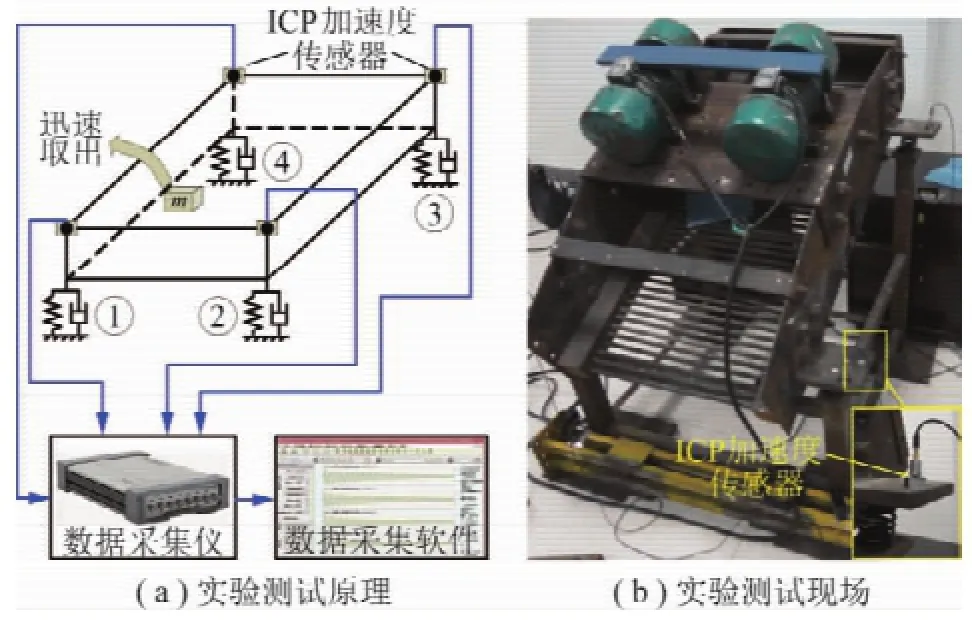
图3　振动筛减振弹簧刚度反演应用实验系统及装置Fig.3　Application test and apparatus for stiffness identification for damping springs of vibrating screen

这里以实验室振动筛模型机为应用实验对象来验证上述基于自由响应的振动筛减振弹簧刚度反演原理的实用性。实验系统及装置如图3所示，将4个ICP加速度传感器(INV9821，分辨率0.002 m/s2，量程50 g，频响范围0.5～8 kHz)通过磁座吸附在筛体各上压板上方，用于测试减振弹簧竖直压缩变形量(Δz1，Δz2，Δz3，和Δz4)的变化加速度，加速度传感器与数据采集仪(INV3060A)相连，通过数据采集软件(DASP－V10工程版)进行信号采集与处理。

一般情况下，振动筛4点支撑减振弹簧的刚度相同，这里用2组簧丝直径不同但自由高度相同的弹簧实现振动筛减振弹簧的刚度不同模拟。弹簧参数见表1，由于簧丝直径尺寸的标准化，选购的模拟故障弹簧有限，其刚度相比初始弹簧，降低约25%。模拟故障弹簧是2号弹簧。

设定系统采样频率为1 024 Hz，定时采样时间为15 s，人为施加脉冲激励使筛体偏平衡而作自由振动。图4为振动筛模型机4个弹簧支撑位置处的自由振动响应(加速度)曲线及对应的功率谱密度函数图，可得到系统的前三阶固有频率分别为4.15，5.05 和6.125 Hz。根据表2中的基本参数，在2号减振弹簧刚度为 32 270 N/m、其他减振弹簧刚度为42 990 N/m的情况下，依据理论模态分析根据各阶固有频率的计算公式=0［9］获得实验振动筛的固有频率计算值分别为4.104 9，4.924 1和6.254 4 Hz。

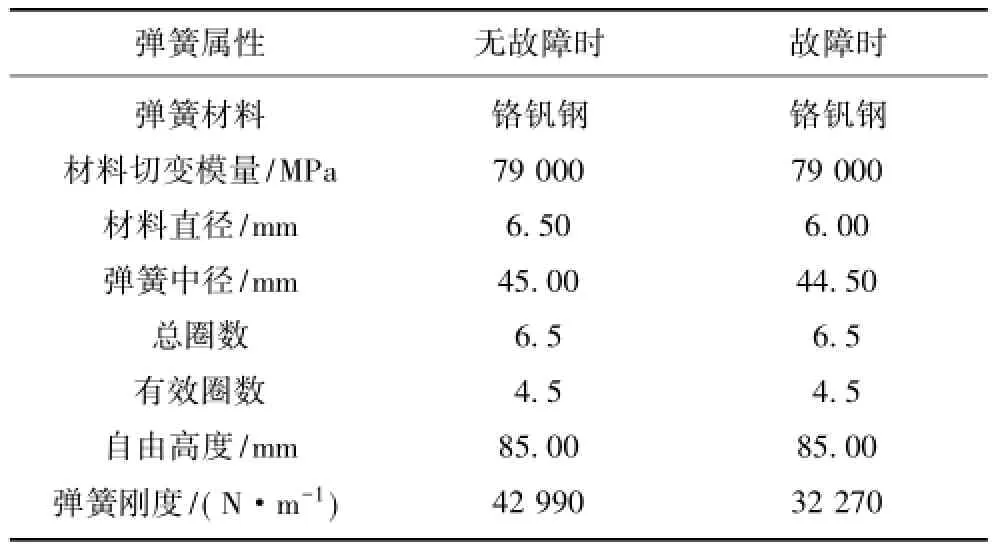
表1　实验用振动筛无故障和故障弹簧的基本参数Table 1　Fundamental parameters of the healthy and the fault springs of the experimental vibrating screen

图4　单个弹簧(No.2)故障时的自由响应曲线及功率谱Fig.4　History of the free response of each plate pressured on spring No.1－4 and the corresponding power spectrum with single spring No.2 fault

表2　实验用振动筛的基本参数Table 2　Fundamental parameters of the experimental vibrating screen

将采集的各个弹簧位置处的筛体自由振动加速度信号，按图2所示的时域中噪声加速度计算速度和位移的数字信号处理过程，进行滤波、积分和去趋势项等操作，如图5所示。加速度、速度和位移随时间递减，且计算所得速度(图5(c))和计算所得位移(图5(e))在去趋势前后均有明显的信号基准的移动，即零漂消除。

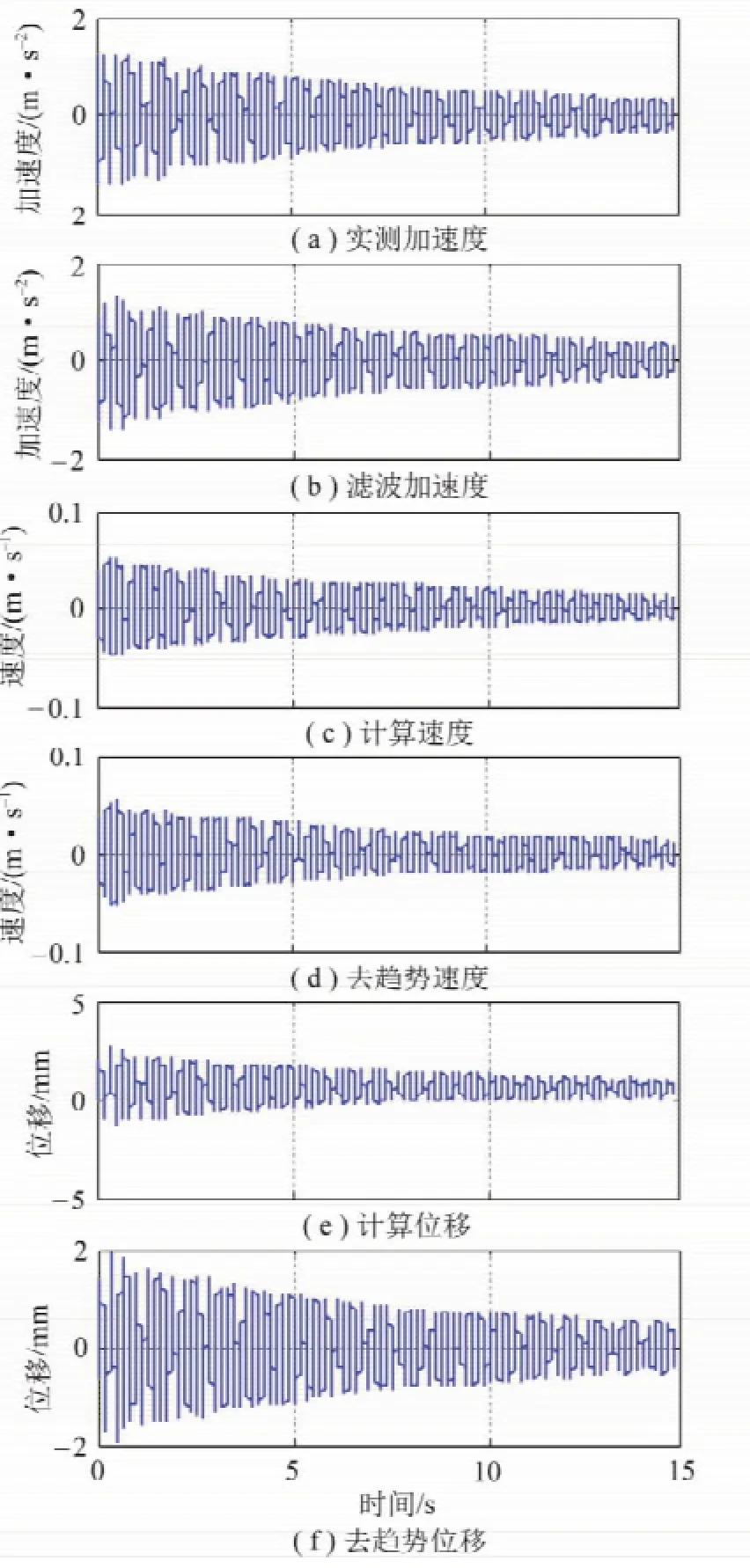
图5　弹簧2故障时的弹簧1处的实测加速度、滤波加速度、计算速度、去趋势速度、计算位移和去趋势位移Fig.5　Free response of spring No.1 with No.2 fault:original acceleration，filtered acceleration，calculated velocity，trendeliminated velocity，calculated displacement and trend-eliminated displacement

结合系统参数(表1，2)，将所示方法处理后的位移、速度和加速度构成自由响应矩阵，根据反演原理得到反演的刚度值。进行4次重复实验，其中，第1次实验k1变化时刚度置信准则变化历程如图6所示，选用的相关参数为:N=8 000，［fu，fd］=［1.00， 20.00］，∈［38.00，47.00］，对应的刚度置信阈值均定为S=0.999 5。

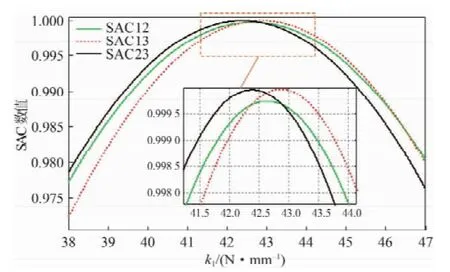
图6　k1变化时刚度置信准则变化历程Fig.6　History of the stiffness assurance criterion with the variable stiffness value of spring No.1

4次实验中，人为随机按压筛体不同位置使之作自由振动，通过提出的反演算法，得到的反演结果列于表3中。很明显，定性来看，2号弹簧故障最严重，与文献［5］的诊断结果一致;定量来看，反演效果均比较理想，与设计值的最大误差仅为3.56%，验证了算法的可行性及稳定性。因此，可以认为基于自由响应的振动筛减振弹簧刚度反演可以实现振动筛各个减振弹簧刚度的定量，进而与设计值进行比较，诊断弹簧状态。

4　结　　论

(1)建立了减振弹簧故障下振动筛非对称动力学模型，推导了减振系统几何位置误差下振动筛空间三自由度运动的振动微分方程。

(2)提出了利用加速度响应获取速度、位移响应的数字信号处理方法，构造系统的响应矩阵，开发了减振弹簧刚度反演基本原理与方法，实现了筛体自由响应反推出各减振弹簧刚度。

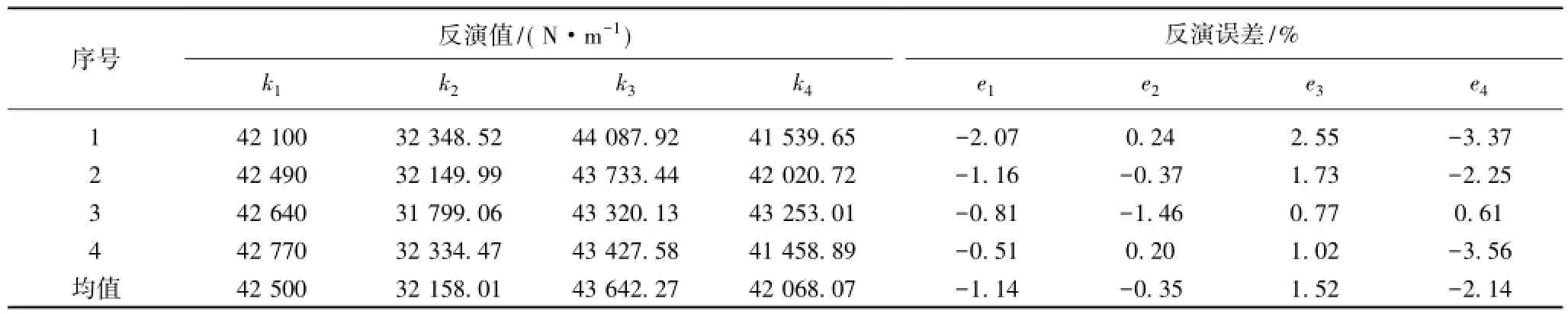
表3　实验获得的刚度反演结果Table 3　Stiffness identification results based on the experiment

(3)研究结果对大型振动筛减振弹簧健康识别及保障设备运行可靠性具有一定的应用价值。

参考文献:

［1］刘初升，蒋小伟，张士民，等．变轨迹等厚筛振动方向角的计算及实验验证［J］．中国矿业大学学报，2011，40(5):737－742．Liu Chusheng，Jiang Xiaowei，Zhang Shimin，et al．Calculation and experimental verification of vibrating direction angle of varying trajectory banana screen［J］．Journal of China University of Mining＆Technology，2011，40(5):737－742．

［2］Zhao Yuemin，Liu Jiongtian，Wei Xianyong，et al．New progress in the processing and efficient utilization of coal［J］．Mining Science and Technology，2011，21(4):547－552．

［3］国家能源局．关于促进煤炭工业科学发展的指导意见［EB/ OL］．http://www．nea．gov．cn/2015－03/25/c_134095304．htm，2015－03－25．

［4］Zhao Yuemin，Liu Chusheng，Li Fengming，et al．Dynamic analysis and optimization of a large-scale vibrating screen with high reliability［A］．XXVIIInternational Mineral Processing Congress(IMPC2014)，2014 ［C］．Chile，Santiago:Gecamin Digital Publications，2014:116－124．

［5］刘初升，彭利平，王宏，等．大型振动筛弹簧故障识别的自由响应法［J］．振动工程学报，2013，26(4):624－632．Liu Chusheng，Peng Liping，Wang Hong，et al．Fault identification for spring of large vibrating screen using free response［J］．Journal of Vibration Engineering，2013，26(4):624－632．

［6］Peng Liping，Liu Chusheng，Li Jun，et al．Static-deformation based fault diagnosis for damping spring of large vibrating screen［J］．Journal of Central South University，2014，21(4):1313－1321．

［7］刘初升，彭利平，赵跃民，等．振动筛减振弹簧故障诊断方法［P］．中国专利:ZL201310134768，2015－04－15．Liu Chusheng，Peng Liping，Zhao Yuemin，et al．Fault diagnosis method for damping springs of vibrating screen［P］．China Patent:ZL201310134768，2015－04－15．

［8］Peng Liping，Liu Chusheng，Wu Jida，et al．Stiffness identification of four-point-elastic-support rigid plate［J］．Journal of Central South University，2015，22(1):159－167．

［9］J．H．金斯伯格．机械与结构振动——理论与应用［M］．白化同，李俊宝，译．北京:中国宇航出版社，2005．

［10］彭利平．大型振动筛减振弹簧刚度反演及梁体动力学问题研究［D］．徐州:中国矿业大学，2015．Peng Liping．Study on stiffness identification for damping springs and dynamic problems of beam structures in a large vibrating screen ［D］．Xuzhou:China University of Mining and Technology，2015．

［11］Wang B T，Cheng D K．Modal analysis by free vibration response only for discrete and continuous systems［J］．Journal of Sound and Vibration，2011，330(16):3913－3929．

［12］Yang Q W，Sun B X．Structural damage identification based on best achievable flexibility change［J］．Applied Mathematical Modelling，2011，35(10):5217－5224．

［13］董聪．现代结构系统可靠性理论及应用［M］．北京:科学出版社，2001．

［14］Pastor M，Binda M，Harˇaarik T．Modal assurance criterion［J］．Procedia Engineering，2012，48:543－548．

中图分类号:TD452;TH135

文献标志码:A

文章编号:0253－9993(2016)06－1568－07

收稿日期:2015－08－14修回日期:2015－10－12责任编辑:许书阁

基金项目:国家自然科学基金资助项目(51221462);中央高校基本科研业务费专项资金资助项目(2015B30214);中国博士后科学基金面上资助项目(2016M590514)

作者简介:彭利平(1987—)，男，江苏江阴人，讲师，博士。E－mail:plpbeckham@163．com

Health identification for damping springs of large vibrating screen based on stiffness identification

PENG Li-ping1，LIU Chu-sheng2，WANG Hong3
(1．College of Mechanical and Electrical Engineering，Hohai University，Changzhou213022，China;2．School of Mechatronic Engineering，China University of Mining and Technology，Xuzhou221116，China;3．Tangshan Research Institute，China Coal Technology and Engineering Group Corp．，Tangshan063012，China)

Abstract:In order to overcome the limitation of qualitatively health identification for damping springs of large vibrating screen(LVS)，a diagnostic methodology for identifying the stiffness of damping springs with free response was proposed．With the geometric position error of the damping system considered，the asymmetric dynamic model of the vibration screen with damping spring fault was established and followed by deriving the vibration differential equation．Then，the discrete free acceleration response data were processed by digital filter，eliminating the trend item and numerical integration，and subsequently constructed in a matrix form to obtain the modified stiffness matrix．Moreover，with disassembling stiffness matrix and defining the stiffness assurance criterion，the principle and procedures for stiffness identification of a large vibrating screen was summarized．Finally，the validity of the developed method for stiffness identification was verified by an experimental test and the error is within 3．56%．The research may accomplish the quantitatively health identification for the damping springs of large vibrating screen．

Key words:vibrating screen;damping spring;stiffness identification;health identification