ANSYS在剪切散斑无损检测系统中的运用

周逸竹，梁志勇，邓忠良

（东华大学，上海 201620）



ANSYS在剪切散斑无损检测系统中的运用

周逸竹，梁志勇，邓忠良

（东华大学，上海 201620）

摘要：用有限元分析的数值模拟方法（ANSYS）研究剪切散斑无损检测，已经受到了人们的极大关注。以剪切散斑无损检测为背景，以有无缺陷试件为模型，对模型进行有限元总体分析，运用计算机数值模拟出在载荷作用下含缺陷试件覆盖层的形变状态。结果表明，当缺陷变化时，对最大离面位移差均有不同程度的影响，未来可以将此方法应用于无损检测中，从而定量检测出缺陷的位置。

关键词：有限元；数值模拟；剪切散斑；无损；缺陷

1　结构缺陷的理论研究

1.1建立结构内部缺陷

建立结构的内部缺陷理论模型，可以简化结构，变成大圆柱体周边被完全固定，其中的一面圆形薄板受到均压作用，出现小挠度弯曲［1］问题，缺陷设计为小圆柱体，圆柱的直径即为缺陷直径，圆柱的厚度即为缺陷的厚度，缺陷深度为缺陷所在的位置距离外表面的距离［2］。

1.2模型理论研究

薄板弯曲的基本方程，又称为弹性曲面的微分方程：

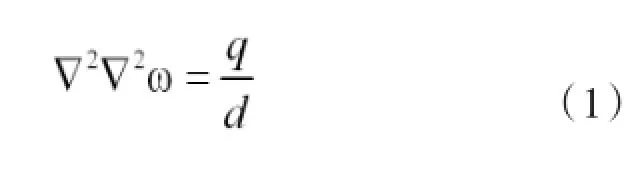
极坐标下，薄板弯曲的基本方程为：

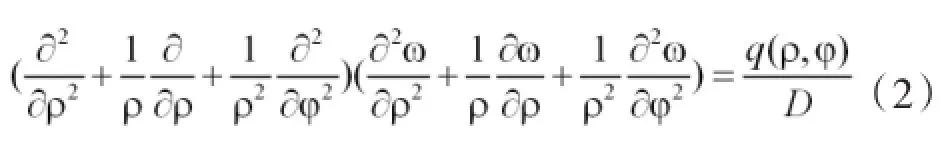
通过常微分方程解答：

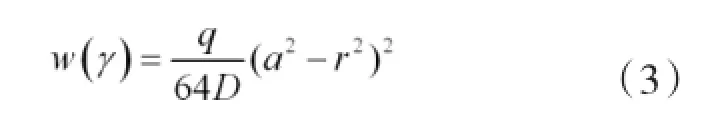
通过大圆薄板的离面位移对r 求导得：

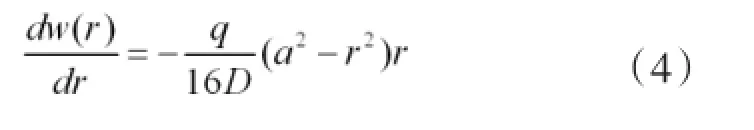
通过大圆薄板的离面位移对x方向求导得：

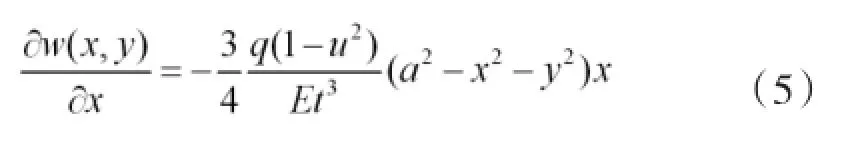
2　结构缺陷的有限元研究

2.1有限单元法介绍

有限单元法最开始应用于工程科学技术上，在计算力学中也被作为其中一种重要的方法来应用，这种数学物理方法在模拟分析解决电磁学、工程力学等方面的问题也起了至关重要的作用。

此单元法中既有理论作为基础，又包含广泛应用的数值分析，它是一种非常有效果的现代力学方法［3］，可以帮助我们解决过去无法用解析方法求解的难题，对于一些复杂的情况，比如不规则的结构形状和边界条件等。

2.2有限元软件的分析过程

一般来说ANSYS 软件的分析过程［4-5］包含3个主要的步骤：前处理（preproeessing）、解题程序（solution）和后处理（postprocessing）。如图1所示。

图1 ANSYS软件分析的3个步骤Fig.1 Three analysis steps of ANSYS

2.3计算设置

研究中首先用软件模拟了一块未含缺陷的圆柱薄板，采用实体建模，类型均为结构分析，直径为D1=100mm，厚度为t=4mm，材料为AL，其属性弹性模量E=0.737×10＂Pa，泊松比u =0.28，在其中一个表面施加均匀载荷压力。在模拟一块含缺陷的圆柱薄板，大小与上述一致，缺陷分为下面几种情况。然后将有无缺陷的最大离面位移数据导出，运用Matlab编程计算，代入具体数据，画出其最大离面位移差，做出图像，如图2所示。

图2 缺陷直径与最大离面位移差的关系Fig.2 Relationship between defect diameter and maximum displacement out-of-plane difference

2.3.1不同直径，相同位置深度的缺陷在相同载荷下

的形变分析

缺陷直径分别为 1mm、2mm、3mm、4mm、5mm、6mm、7mm、8mm、9mm、10mm。缺陷厚度为t=2mm，缺陷位于大圆柱的中心。模型建立以后，自由划分单元网格，在大圆柱表面均匀施加载荷2kp。

2.3.2相同直径位置深度的缺陷在不同压强下的形变

分析

研究中模拟了相同缺陷直径在不同压强作用下的变化，即缺陷的直径位置深度都相同，而压强不同时，各个试件模型在不同载荷即压强作用下的最大离面位移差，如图3，试件模型采用的缺陷深度为t=2mm，直径2mm位于大圆柱的中心圆柱体。压强分别为1kp、2kp、3kp、4kp、5kp、6kp、7kp、8kp、9kp、10kp。

图3 压强与最大离面位移差的关系Fig.3 Relationship between pressure and maximum displacement out-of-plane difference

2.3.3相同压强直径位置的缺陷在不同深度的形变分

析

缺陷的直径压强位置相同，缺陷的深度不同时，各个试件模型在不同载荷即压强作用下的最大离面位移差，如图4，试件模型采用的缺陷直径2mm，位于大圆柱的中心圆柱体，压强为2kp，深度为0.2mm、0.4mm、0.6mm、0.8mm、1.0mm、1.2mm、1.4mm、1.6mm。

图4 缺陷深度与最大离面位移差的关系Fig.4 Relationship between defect depth and maximum displacement out-of-plane difference

2.3.4相同压强直径深度的缺陷在不同位置的形变分

析

缺陷的半径深度以及所受载荷相同，缺陷的位置不同时，各个试件模型在不同载荷作用下的最大离面位移差，如图5，试件模型的模拟采用的缺陷直径a=2mm，深度2mm，压强为2kp的圆柱体，缺陷圆心距中心位置为 3mm、6mm、9mm、12mm、15mm、18mm、21mm、24mm、27mm、30mm。

图5 缺陷距离与形变大小的关系Fig.5 Relationship between defect distance and size of deformation

3　结果与讨论

通过以上模拟分析发现，在同一载荷作用下，试件模型的缺陷直径越大，形变量也越大。在缺陷相同作用下，试件模型的压力越大，随之形变也越大。在同一载荷作用下，试件模型的深度离施加载荷的面越远，形变量越小。在同一载荷作用下，试件模型的缺陷离中心距离越远，形变量反而越小。

4　结论

用有限元分析的数值模拟方法（ANSYS）研究剪切散斑无损检测，模拟出在载荷作用下含缺陷试件覆盖层的最大离面位移，在通过后期分析以及优化，并应用Matlab与未含缺陷的模型进行对比，可以得出以下结论：

第一，改变数值模拟原始条件，可以得出不同载荷作用下最大离面位移差，为实验提供了理论基础，缺陷的各项参数均与最大离面位移差有关，且关系密切。

第二，同时也为以后定量检测缺陷提供了基础和方向。根据最大离面位移差图，由以上4种拟合的曲线，就可以在检测缺陷的时候，通过其最大离面位移推断缺陷尺寸等。如果对内部缺陷的定量检测可以通过该模型，那么就可以省掉做实验的环节。

参考文献：

［1］吴家龙.弹性力学［M］.北京：高等教育出版社，2001.

［2］吴愧.电子散斑干涉法在结构内部缺陷检测中的应用研究［D］.上海：同济大学，2008.

［3］王敏. 数字散斑剪切干涉结构缺陷检测研究［D］.南京：南京航空航天大学，2011.

［4］罗飞华. MATLAB GUI 设计学习手册［K］.北京：北京航空航天大学出版社，2009.

［5］ANSYS.Element Reference，［M］.ANSYS HELP，2002.

中图分类号：TH878

文献标志码：A

文章编号：1674-8646（2016）10-0014-03

收稿日期：2016-03-01

作者简介：周逸竹（1992-），女，黑龙江鸡西人，在读研究生，主要从事固体力学研究。

Application of ANSYS in speckle-shearing NDT system

ZHOU Yi-zhu， LIANG Zhi-yong， DENG Zhong-liang
（Donghua University， Shanghai 201620， China）

Abstract：Taking use of ANSYS to study speckle-shearing nondestructive testing has attached great concern of people. Taking speckle-shearing NDT as the background，and non-defective specimen as a model，this paper made general analysis of the model finite element，stimulated deformation state of defective specimen coating under the effect of loading. The results showed that the changes of defect has affect on maximum displacement out-of-plane difference in varying degrees，and this method can be applied to NDT in the future so as to quantitatively detect defect location.

Key words：Finite element； Numerical simulation； Speckle-shearing； Non-destructive； Defect