基于切片原理的海量点云并行简化算法

官亚勤 赵学胜 王鹏飞 李大朋

摘要：针对传统点云简化算法效率低且处理点数少的缺陷，结合快速成型领域的切片原理顾及特征计算复杂度低的特点，设计并实现了适合千万级海量激光雷达（LiDAR）点云的并行切片简化算法。该算法根据切片原理对点云模型分层并按照角度排序，利用NVIDA的统一计算设备架构（CUDA）和可编程图形处理器（GPU）高度并行的性能优势，使用GPU多线程高效并行地执行单层切片点云简化，提高了算法效率。最后，应用3组不同数量级点云模型分别进行简化对比实验。实验结果表明：在保持模型特征与压缩比不变的情况下，所提算法效率高出传统基于CPU的串行切片算法1～2个量级。

关键词：

海量点云；简化；切片法；计算设备架构；图形处理器；并行计算

中图分类号： TP391.413 文献标志码：A

0引言

随着大规模精细三维模型获取技术的不断发展，三维激光扫描技术凭借其数据获取速度快、精度高、覆盖广的特点，成为高精度三维模型数据获取的主流方式之一，获取的点云数据量也呈几何级数增长，因此，如何对海量散乱点云数据进行简化已成为计算机图形学、快速成型、三维测绘、地理信息系统、数字城市、军事仿真、游戏娱乐等点云模型应用领域的重要研究课题之一。

传统的点云简化方法主要分为两个大类：第一类是顾及特征的简化[1-3]，此类算法需要依据单点的K邻近点集拟合曲面，并构建曲面的法向量和曲率等相关特征度量因子判定单点是否为特征点，从而实现点云简化。这些算法能够保持模型特征，但是涉及K邻近点集等复杂计算操作，耗时多，仅适用于小数据量的点云简化。第二类是规则采样简化算法[4-6]，此类算法依据一定规则对原始点云进行采样，然后以采样点作为特征点保留，剔除其他点实现点云简化。这类算法简化效率高，但是不能有效地保持模型特征，由于采样标准单一，在特征变化明显的尖锐弯曲处会导致局部细节过度光顺丢失细节。由此可见，传统算法的主要问题是点云简化过程中计算复杂与模型特征保持不能兼顾。

近年来通用计算图形处理器（General Purpose Graphics Processing Unit， GPGPU）的快速兴起，尤其是NVIDIA公司2006年推出的图形处理器（Graphics Processing Unit， GPU）并行计算框架——统一计算设备架构（Compute Unified Device Architecture， CUDA）[7]凭借其高性价比、低通信开销、卓越的并行计算能力，让海量化或者计算复杂度高的三维点云模型数据快速处理成为可能。文献[8]使用GPGPU实现基于边缘点的激光雷达（Light Detection And Ranging， LiDAR）点云滤波算法，文献[9]提出一种基于CUDA的双边滤波的点云滤波算法。两者都将K邻近点、曲面拟合、法向量以及曲率等计算复杂度高的步骤，利用CUDA编写不同的kernel并行化，从而加速点云简化，但是，由于在单个线程中完成类似求解单点K邻近点的计算需要消耗太多的全局内存等GPU资源，这严重制约此类算法处理点云的规模，仅适用于数十万级的小规模点云处理。

本文借助众核GPU通用计算高性能并行的特点，结合快速成型领域切片点云简化算法[10-12]顾及特征的优势，实现了基于CUDA的顾及模型特征且适合千万级点云的并行简化算法，并从该算法的时间效率方面的优势阐述了CUDA用于海量数据处理的优势和潜力。

1切片点云算法原理

基于CUDA的切片算法实现原理如下：首先，在CPU端根据点云的几何分布特征对点云进行分层并降维投影至相应的投影平面上；然后，依次对不同投影面上单层点云中的每一点和相应投影平面坐标原点所连直线与投影面某一坐标轴固定方向的夹角大小进行升序排序；最后，使用本文提出的利用CUDA在GPU端对每层排序后的切片点云依据弦高差法并行计算各点的弦高差值和各层切片的弦高差均值作为阈值，通过比较各点弦高差与阈值的关系，确定该点是否为特征点从而完成该层切片简化。

1.1特征点的提取原理

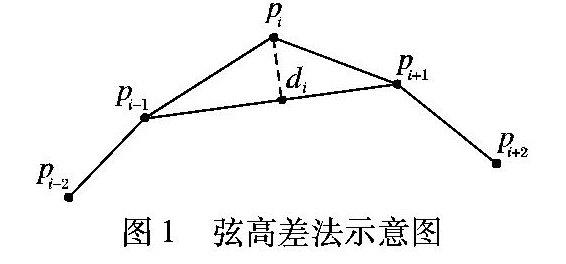
利用弦高差法来确定切片中各点是否为特征点，原理详见文献[13]，其中弦高距离由式（1）求得：

di=|Axi+Byi+C|/A2i+B2i+C2i（1）

如图1所示，pi为目标待判定点，直线pi-1pi+1所构成直线方程为l：Ax+By+C=0，由计算几何的原理可求得pi到直线l的垂直距离为di。

其中：mj表示第j层点云的总数；di表示第j层点云中的第i个点的弦高差值。

1.2基于CUDA的切片算法实现

由上述原理可以看出：依次计算单点的弦高差、单层切片的阈值σ以及单点弦高与阈值的比较等操作均是计算密集的操作，不涉及对原始切片数据的写操作，不会因为数据的复写而引发数据的二义性，具备良好的数据独立性，因此本文借助NVIDIA推出的GPGPU平台CUDA的单程序多数据（Single Program Multiple Data， SPMD）特性[7]，利用GPU中大规模并行处理器的并行计算能力，使用相互独立的线程并发执行这些计算，实现基于数据并行性的点云简化，具体算法如下。

步骤1将依据角度排序后的单层点云切片从CPU的cpuvector中传入至GPU的gpuvector中。

步骤2结合CUDA，设定核函数的线程块数量blockDim.x和线程块中线程数量threadDim.x，启动核函数BowstringCaculate_kernel并行计算出每一点的弦高差值并存入GPU显存的数组Height中。

步骤3在GPU中用并行归约算法求出该层切片的弦高差均值σ，作为该层切片的特征判定阈值。

步骤4启动核函数isFeaturePoint_kernel，根据BowstringCaculate_kernel返回的各点弦高Height与阈值σ，确定该层切片中的特征点，并将计算结果存入数组isFearturePoint中。

步骤5将isFearturePoint数组中的元素利用CUDA的核函数cudaMempy传回至CPU端，在CPU端根据对应索引位置的值决定cpuvector相应位置上的点保留与否，从而得到简化后的点云SimplyfiedVector。

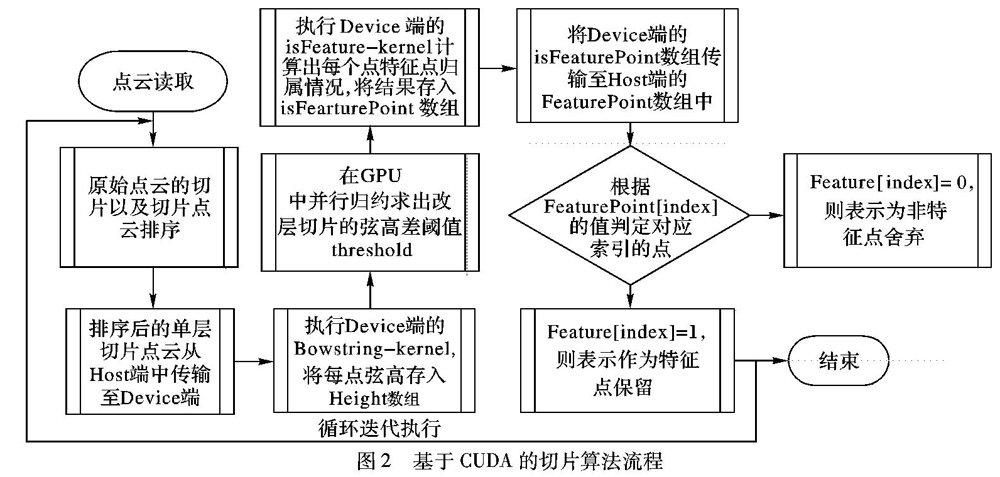
步骤6回到步骤1继续对其他切片层的点云简化。算法中的流程如图2所示。

其中，执行单层切片点云弦高差计算的核函数BowstringCaculate_kernel的伪代码如下。

算法BowstringCaculate_kernel。

有序号的程序——————————Shift+Alt+Y

程序前

输入：LayerPoints为排序后的单层切片点云的坐标数组；Size表示该层切片的点云数量。

输出：Height为用于保存每个线程计算的弦高差值的数组。

1）

Dim index ← threadInx.x+blockIdx.x*blockDim.x；

2）

Dim *leftPoint，*rightPoin；

3）

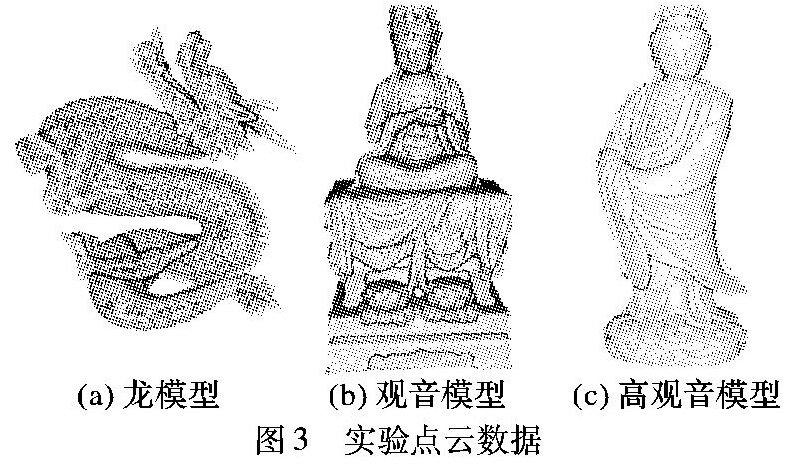
if（index

4）

Loop index from 0 to Size Do

5）

leftPoint ← LayerPoints+index-1；

6）

rightPoint ← LayerPoints+index-1；

7）

if（index==0）Then

8）

leftPoint ← LayerPoints+Size-1；

9）

End if

10）

if（index==Size-1）

11）

rightPoint ← LayerPoints+index-（Size-1）；

12）

End if

13）

Height[index] ← calculateHeight（leftPoint；

14）

LayerPoint[index]，rightPoint）；

15）

index ← index+blockDim.x*GridDim.x；

16）

End Loop

17）

End if

程序后

其中，calculateHeight为计算单点的弦高函数，其实现原理如式（1）和图1所示。

2实验分析

实验平台配置如下：Windows 7操作系统，CPU为Intel Core i53470 @ 3.20GHz 3.60GHz，内存为4.0GB（3.28GB可用），显卡为NVIDIA GeForce GT 640。在该平台下使用C++语言结合Visual Studio2010和NVIDIA的CUDA6.0框架实现本文算法。

算法实验的模型数据如图3所示：龙模型共437645个点，大佛模型共有1753052个点，高观音模型共11807207个点。

本文使用上述3个不同数量级的点云模型，对本文提出的基于CUDA的切片点云简化算法（简称GPU切片算法）与基于CPU的切片点云简化算法[13]（以下简称CPU切片法）进行对比实验。

其中：弦高差阈值由式（1）求出，切片方向均为z轴，依次选取切片数量laynum为10，25，50，75，100作5组对比实验，结果如表1所示。

通过表1，可依次求得上述3个不同数量级模型的算法耗时与切片层数的关系曲线如图4所示。

其中图4中的折线图（a）、（b）、（c）依次表示龙模型、观音模型以及高观音模型的算法耗时与切片层数的对应关系，（d）表示龙模型、观音模型以及高观音模型对应的CPU切片法与GPU切片法的加速比（其中加速比等于CPU算法执行时间除以GPU算法执行时间）与切片层数的对应关系。

从表1呈现的数据以及图4的折线图（a）、（b）、（c）呈现的线条走势可以看出：在两种算法对应的压缩率基本一致基础上，本文提出的GPU切片算法的效率比传统CPU算法高出10～30倍，约1～2个量级；但是，随着切片层数的增加，本文提出的GPU算法耗时有一定程度的增加。因为在CUDA架构的切片算法中（流程如图2所示），随着切片层数的增加，CPU和GPU之间进行I/O交互的次数也随之增加，最终导致算法的执行时间有一定程度的增加。从图4（d）可以看出：龙模型和观音模型的加速比，均随着切片层数增加有一定程度的减小。而数据量多达千万个点的高观音模型，其加速比曲线变化相对平稳。这是由于GPU更适合于密集型的计算，当数据量（计算量）较小时，算法在GPU上的执行时间无法隐藏访问和数据传输的延迟，而随着数据量的增大，这些延迟逐渐被隐藏，因此加速比逐渐增大。而当数据量增大一定的程度，GPU近乎满负荷的工作，所有的访问和数据传输的延迟都已被很好地隐藏，加速比也趋于稳定如高观音模型的加速比曲线所示。

此外，以模型特征最为明显的观音模型为例，依次选取该模型切片数为25，50，75的底座前侧简化局部视图，如图5所示。发现当切片层数为25时，由于压缩率粒度太大导致底座衣服褶皱与莲花形等多处被过度平滑，特征丢失太严重；切片层数为75时，由于压缩粒度太小导致残留的冗余点较多；而切片层数为50时，底座衣服褶皱与莲花形的特征细节完整保持，而且冗余的点较少，简化效果是较为理想，因此，对不同的模型选取合适的切片层数对模型简化至关重要。

3结语

本文利用CUDA的高性能并行计算优势，对传统基于CPU的串行切片点云简化算法进行了改进，将传统算法的核心步骤：单点的弦高差计算与特征点判定算法逻辑并行化，通过对不同数量级的3个点云模型的简化实验，得出以下结论：

1）对于同一模型，GPU算法尽管随着切片层数的增加，耗时由于数据交互次数增加有一定程度的小幅震荡，但均远少于传统CPU算法。

2）对于不同数量级的模型，加速比曲线随着点云数量的增加而逐渐稳定，且加速效果更优，验证了本文算法应对海量点云简化的优势和潜力。

3）模型的特征保留完整性与切片层数无直接关系，仅仅与模型表面特征有关。

下一步主要工作是在CPU端使用多线程并行技术，提高点云切片分层排序的速度；应用GPU架构中不同访问性能的内存模型和基于任务并行性的流水线模型对算法进行优化。

参考文献：

[1]

周煜，张万冰，杜发荣，等.散乱点云数据的曲率精简算法[J].北京理工大学学报，2010，30（7）：785-790.（ZHOU Y， ZHANG W B， DU F R， et al. Algorithm for reduction of scattered point cloud data based on curvature [J].Transactions of Beijing Institute of Technology， 2010， 30（7）： 785-790.）

[2]

李义琛，庞明勇.基于二次误差度量的点云简化[J].小型微型计算机系统，2012，33（11）：2538-2543.（LI Y C， PANG M Y. Decimating point cloud based on quadric error metric [J]. Journal of Chinese Computer Systems， 2012， 33（11）： 2538-2543.）

[3]

王先泽，李忠科，张晓娟，等.特征保持的基于紧支径向基函数的点云简化[J].计算机工程与设计，2013，34（1）：201-206.（WANG X Z， LI Z K， ZHANG X J， et al. Feature preserving simplification of point cloud based on CSRBF [J]. Computer Engineering and Design， 2013， 34（1）： 201-206.）

[4]

胡志胜，于敬武，述涛.一种结合了栅格化和特征判断的点云压缩方法[J].辽宁工程技术大学（自然科学版），2015，34（8）：958-963.（HU Z S， YU J W， SHU T.A point cloud compression approach combined with rasterizing and feature estimate [J]. Journal of Liaoning Technical University （Natural Science）， 2015， 34（8）： 958-963.）

[5]

邢正全，邓喀中，薛继群.基于栅格划分和法向量估计得点云数据压缩[J].测绘通报，2012（7）：50-54.（XING Z Q， DENG K Z， XUE J Q. Point cloud data compression based on grid division and normal vector estimation [J]. Bulletin of Surveying and Mapping， 2012（7）： 50-54.）

[6]

邵正伟，席平.基于八叉树编码的点云数据精简方法[J].工程图学学报，2010，31（4）：73-77.（SHAO Z W， XI P. Data reduction for point cloud using octree coding [J]. Journal of Engineering Graphics， 2010， 31（4）： 73-77.）

[7]

赵开勇，汪朝辉.大规模并行处理器编程实战[M].2版.北京：清华大学出版社，2013：36-40.（ZHAO K Y， WANG C H. Programming Massively Parallel Processors： a Handson Approach [M]. 2nd ed. Beijing： Tsinghua University Press， 2013： 36-40.）

[8]

崔放，徐宏根，王宗跃.基于GPGPU的并行LiDAR点云滤波算法[J].华中师范大学学报（自然科学版版），2014，48（3）：431-436.（CUI F， XU H G， WANG Z Y. A point cloud filtering algorithm based on GPGPU parallel computing [J].Journal of Huazhong Normal University （Natural Science）， 2014， 48（3）： 431-436.）

[9]

唐杰，徐波，宫中樑，等.一种基于CUDA的三维点云快速光顺算法[J].系统仿真学报，2012，24（8）：1633-1638.（TANG J， XU B， GONG Z L， et al. Fast fairing of 3D point cloud using CUDA [J].Journal of System Simulation， 2012， 24（8）： 1633-1638.）

[10]

PARK H T， CHANG M H， PARK S C. A slicing algorithm of point cloud for rapid prototyping [C]// Proceedings of the 2007 Summer Computer Simulation Conference. San Diego， CA： Society for Computer Simulation International， 2007： Article No. 24.

[11]

SHIN H， PARK S. Direct slicing of a point set model for rapid prototyping [J]. ComputerAided Design and Applications， 2004， 1（1/2/3/4）： 109-115.

[12]

PERCOCO G， GALANTUCCI L. Localgenetic slicing of point clouds for rapid prototyping [J]. Rapid Prototyping Journal， 2008， 14（3）： 161-166.

[13]

方芳，程效军.海量散乱点云快速压缩算法[J].武汉大学学报（信息科学版），2013，38（11）：1353-1357.（FANG F， CHENG X J. A fast reduction method for massive scattered point cloud based on slicing [J]. Geomatics and Information Science of Wuhan University， 2013， 38（11）： 1353-1357.）

[14]

徐工，程效军.基于小波技术的散乱点云自适应压缩算法[J].同济大学学报（自然科学版），2013，41（11）：1738-1743.（XU G， CHENG X J. Adaptive reduction algorithm of scattered point clouds based on wavelet technology [J]. Journal of Tongji University （Natural Science）， 2013， 41（11）： 1738-1743.）