Simth串级PID控制在锅炉主蒸汽温度控制中的应用

冯慧山

(中国石油化工股份有限公司 天津分公司，天津 300271)



Simth串级PID控制在锅炉主蒸汽温度控制中的应用

冯慧山

(中国石油化工股份有限公司 天津分公司，天津 300271)

摘要：针对主蒸汽温度存在较大的滞后、非线性问题，传统的PID控制无法满足高精度控制，而工厂现用DCS中又没有先进控制方法。通过对Simth预估器的匹配程度，利用Matlab仿真，表明预估模型偏差较大时仍然可以达到比PID控制好的效果，而且加入该预估器不会增加控制器的负荷率。利用DCS中现有的算法包搭接了Simth预估器，结合串级PID控制，实现了CFB锅炉的主蒸汽温度控制，取得了较好的效果。

关键词：主蒸汽温度锅炉PID控制Simth预估

锅炉主蒸汽温度是锅炉控制的主要参数之一，其控制效果的好坏直接关系到蒸汽的品质，影响机组经济运行[1]。锅炉主蒸汽温度为复杂的受控对象，而且均有较大的滞后情况，燃烧变化、烟气变化、手动干预的减温水量变化、外部主蒸汽负荷的变化、一/二次风的变化均会使主蒸汽温度受到影响。针对上述因素，主蒸汽温度的控制既要求对外扰有较快的响应速度以及回稳率，又要求对减温水压力变化有较强的抑制力，使系统具有良好的稳定性，保证高品质的蒸汽。而对于目前常规DCS软件算法均为模块架构，控制回路搭接主要是传统的PID控制，或者为串级PID控制，并引入负荷、燃料量等信号的前馈，虽然如此对于大滞后的主蒸汽温度控制来说，实际运行的动态效果仍然偏差大、过渡时间长、动态摆动，无法满足高精度控制要求。而对于模糊控制、神经网络控制、滑膜控制、无辨识预估控制等智能控制方法，虽然在主蒸汽温度控制研究中实现了较好的效果，但由于其运算的复杂以及DCS平台的制约而无法在DCS中实现，由外挂APC控制的计算机实现，会增加很大的投入费用。因此，笔者借助Matlab软件的Simulink建立数学模型，仿真分析实现了Simth预估-串级PID的锅炉主蒸汽温度控制，并结合Matlab搭接方法，使用Ovation DCS中现有的软件基础算法，搭接了Simth预估-串级PID控制程序，实现了主蒸汽温度的控制，并取得了较好的效果。

1蒸汽温度控制系统工艺流程

某厂CFB锅炉的减温水控制系统分为两级减温4个控制回路，分别为甲侧一级减温水、甲侧二级减温水、乙侧一级减温水以及乙侧二级减温水控制，这4路控制均为将过热蒸汽与水中和，目的是使过热蒸汽焓值降低，从而降低主蒸汽温度，以保证屏翼过热器和高温过热器炉管不超温，并控制主蒸汽出口温度的目的。减温水工艺流程如图1所示。

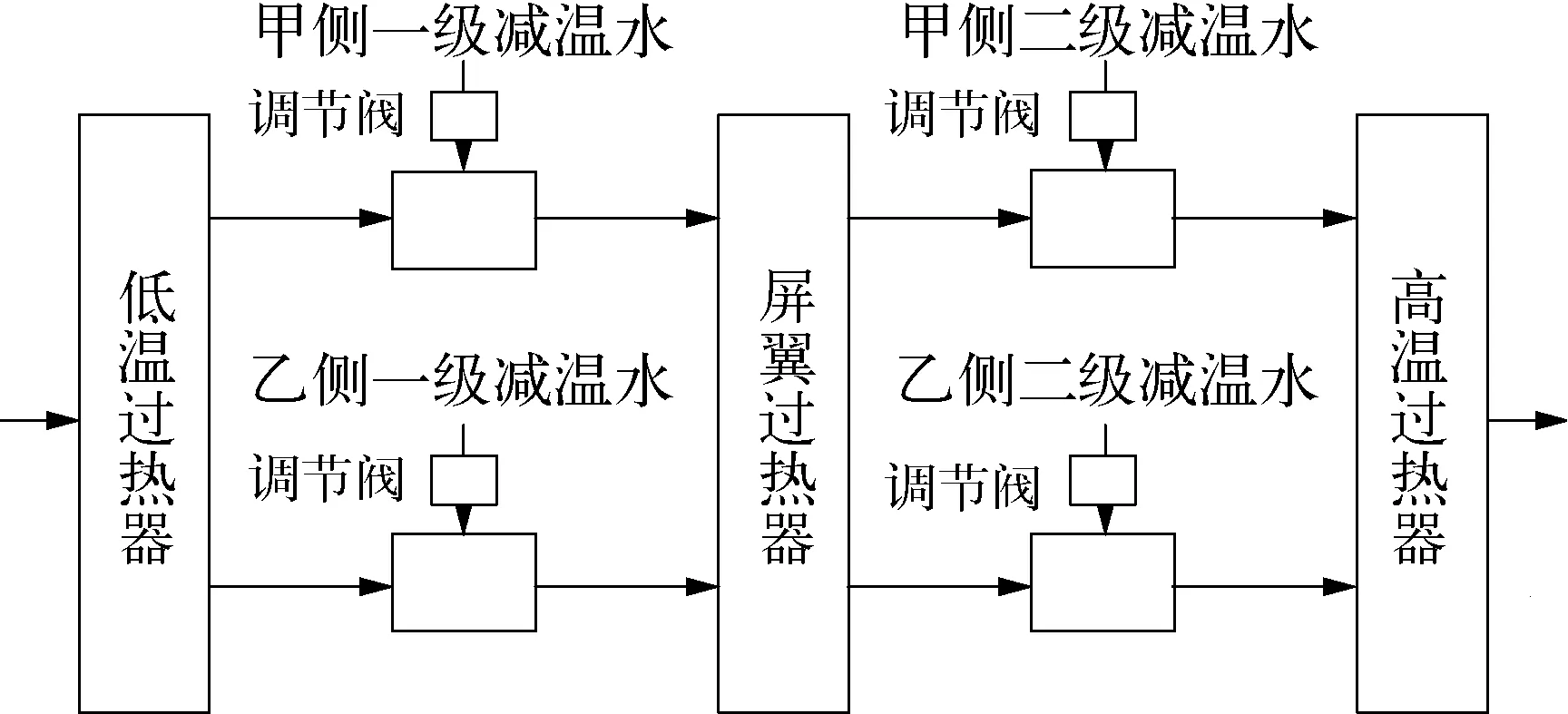
图1　主蒸汽温度控制工艺流程示意

2蒸汽温度模型辨识

锅炉过热蒸汽温度动态响应具有大滞后、非线性等特点，加之阀门的流通性变化以及减温水压力变化，其精确的数学模型很难建立。因此，考虑利用Matlab对实际响应数据进行离线辨识[2-3]，采用最小二乘法的辨识算法，建立阀门开度-减温水后温度、减温水后温度-主蒸汽温度两个传递函数模型，如甲侧二级减温水的辨识模型为

(1)

(2)

由式(1)、式(2)可知导前区和惰性区这两个环节均有一定的滞后，尤其是传递函数G2(s)，滞后

47s。因此，在传统PID或串级PID控制该对象时无法达到较好、高精度的控制。

3Simth预估控制器

预先预估过程基本扰动下的动态特性，再由预估器进行补偿的过程控制方案，能够很好地解决大滞后的问题[4]，也就是通常所说的Smith预估控制，该控制结构如图2所示。

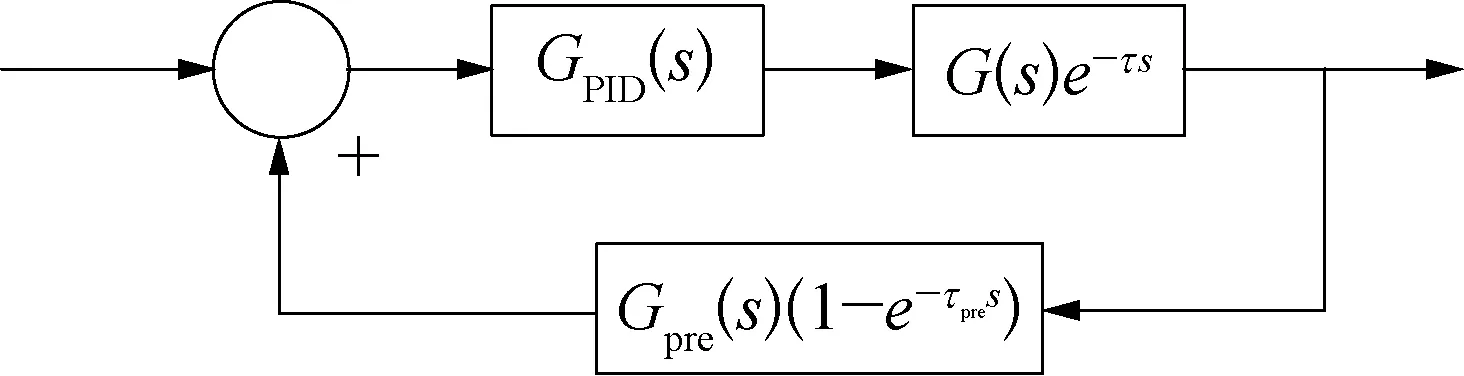
图2　Smith预估控制器结构示意

其被控对象为G(s)e-τs，Smith预估控制器为Gpre(s)(1-e-τpres)，控制器为GPID(s)。当Gpre(s)=G(s)，τpre=τ，预估模型与系统模型无误差，这样整体模型闭环传递函数中就不含滞后环节，消除了滞后环节对系统调节品质的影响，其动态响应只为一般滞后环节，即可以认为是调节的延时，补偿后的闭环传递函数为

(3)

4基于Matlab的蒸汽温度仿真

4.1蒸汽温度三种控制方式比较

对于上述主蒸汽温度传递模型，分别利用单PID控制、串级PID控制、Smith-串级PID控制三个方案进行控制，其中Smith模型为完全匹配辨识模型，Simulink框图如图3所示。

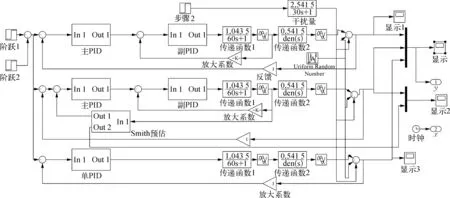
图3　单PID/串级PID/Smith-串级PID的控制示意

整定单PID参数为KP=4.3，KI=0.015；整定串级PID参数其主控制器的KP=4.3，KI=0.015，副控制器的KP=1，KI=0.01；Smith-串级PID控制器其主控制器的KP=4.3，KI=0.015，副控制器的KP=1，KI=0.01，Smith预估模型为

(4)

在800s引入一阶扰动时，仿真结果如图4所示。

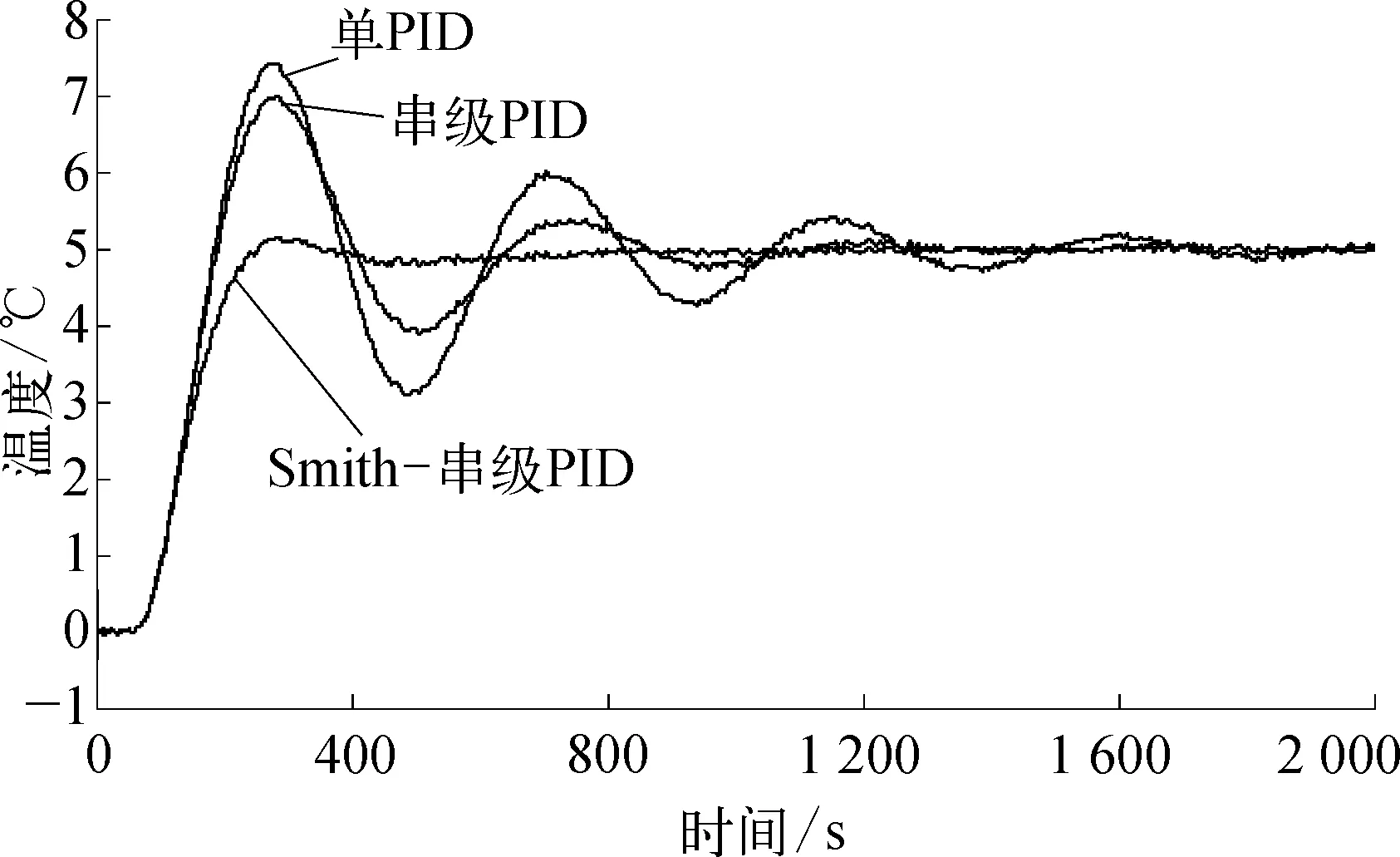
图4　三种控制方案的仿真结果比较

由仿真结果可以看出Smith串级PID控制器的控制效果优于单PID和串级PID的控制效果，超调量几乎没有，控制效果良好。

4.2三种控制方式对扰动控制效果的比较

4.2.1引入无惯性的一阶环节

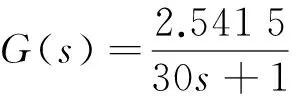
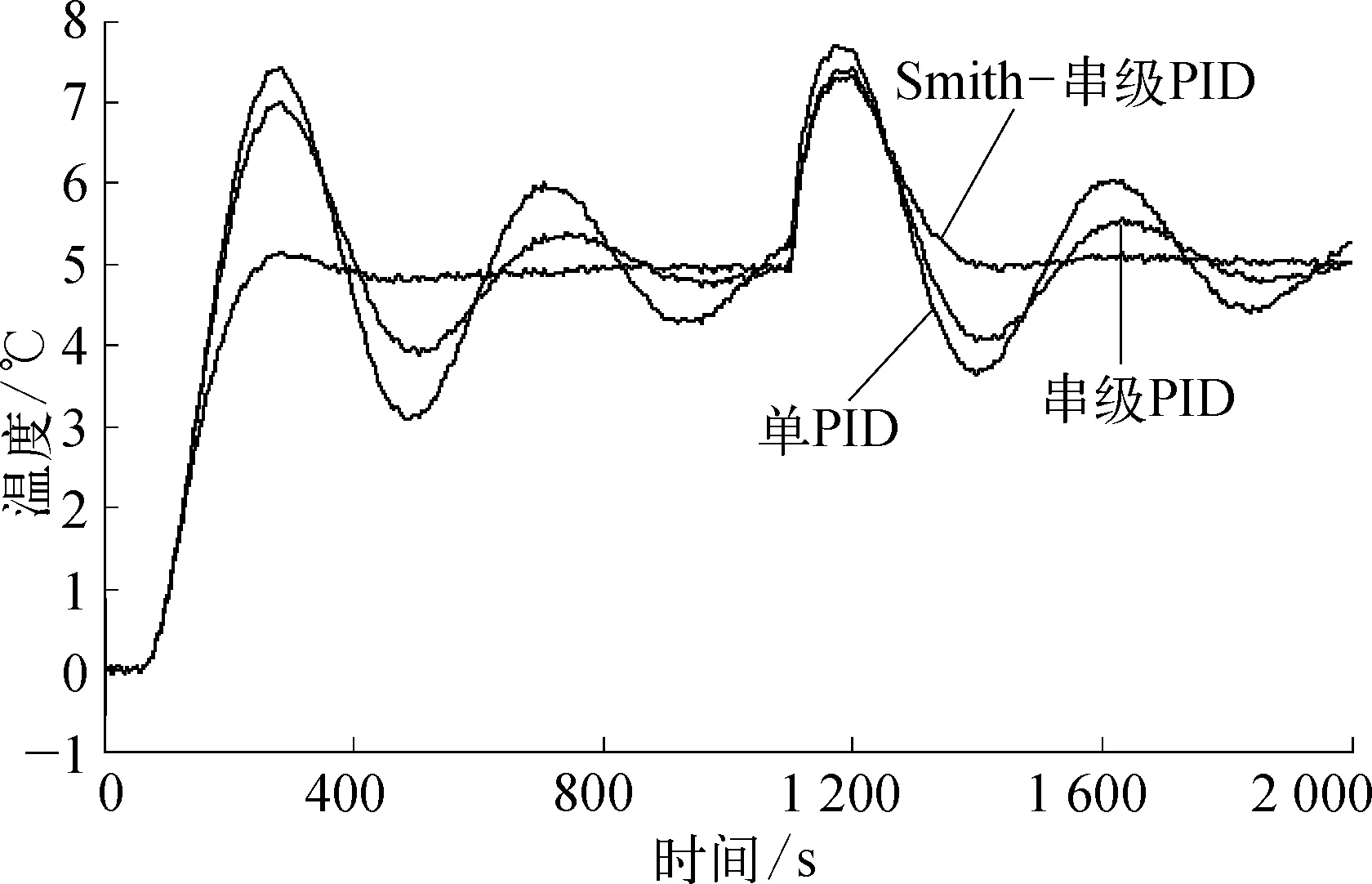
图5　三种控制方案加入扰动后的控制效果示意

由此可见，加入扰动控制后Smith-串级PID控制有较好的控制效果。

4.2.2引入惯性的一阶环节

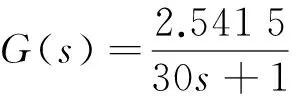
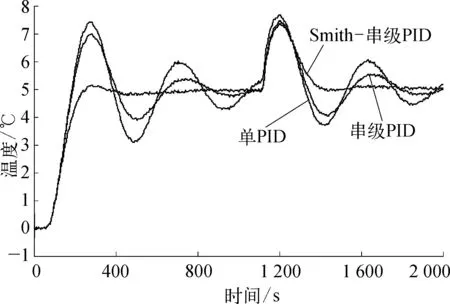
图6　加入一阶惯性环节后的控制效果示意

由此可见，加入扰动控制后Smith-串级PID控制仍然有较好的控制效果。

4.3改变预估模型的控制效果比较

针对预估模型适配情况对Smith-串级PID控制效果的影响，分别设置了四种情况：

4.3.1原预测模型

在三种控制方式下，不改变预测模型，在800s引入一阶扰动时，仿真结果如图4所示，原预测模型如式(5)所示。

(5)

4.3.2改变延时时间的预测模型

在三种控制方式下，改变了预测模型的延时时间，与式(5)比较，式(6)将延时时间降为20s，式(7)将延时时间增加到70s，仿真结果如图7所示。

(6)

(7)

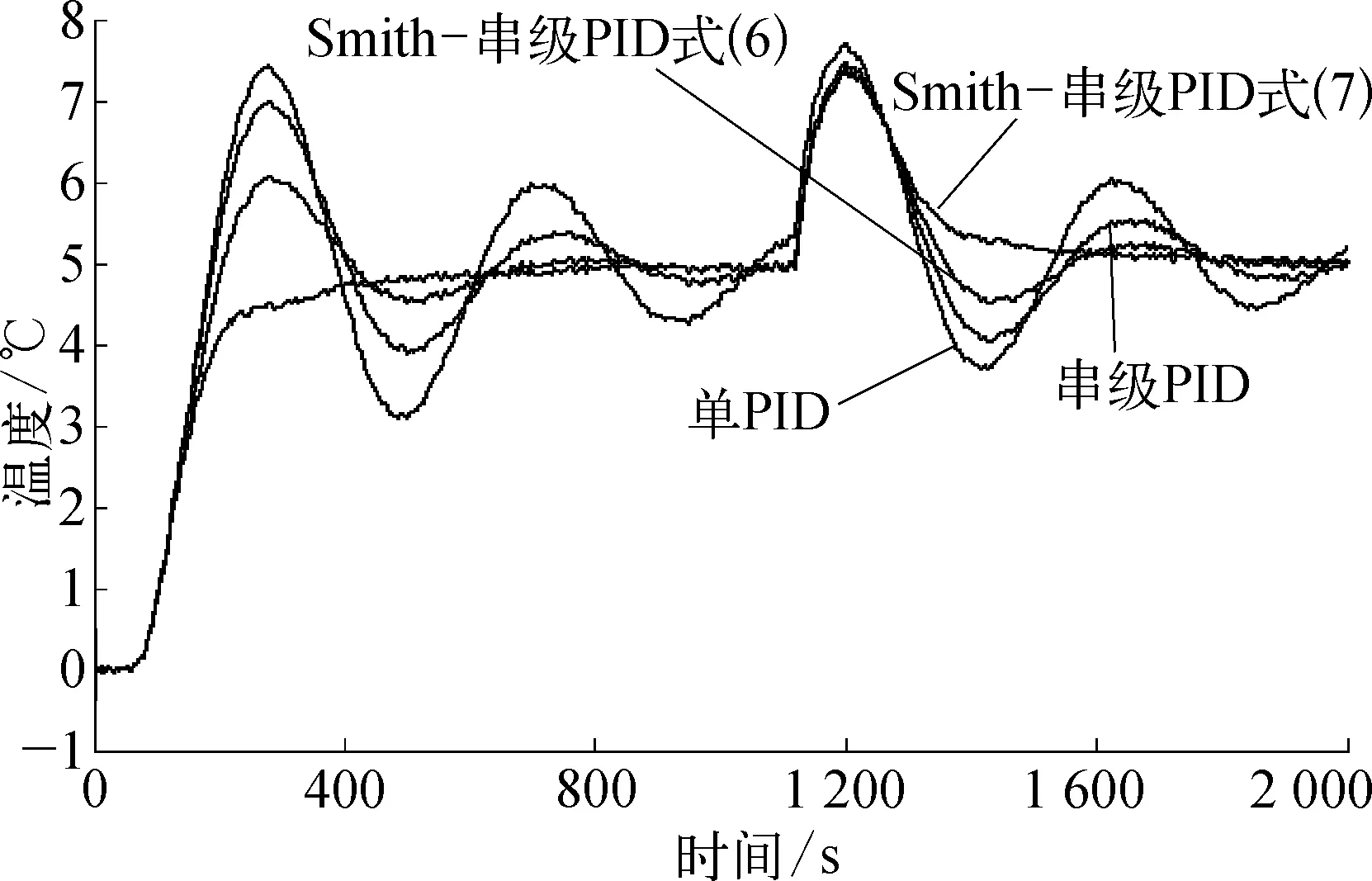
图7　改变预测模型延时时间的控制效果示意

由图7可知，虽然改变了延时时间，但是Smith-串级PID控制效果仍然比串级PID以及单PID控制效果好。

4.3.3改变为一阶响应模型

在三种控制方式下，将预测模型由原来的二阶模型变为一阶模型，并将变量前的系数分别修改为60和10，仿真结果如图8所示，虽然修改了系数，但控制效果始终比串级PID和单PID控制效果好。

(8)

(9)

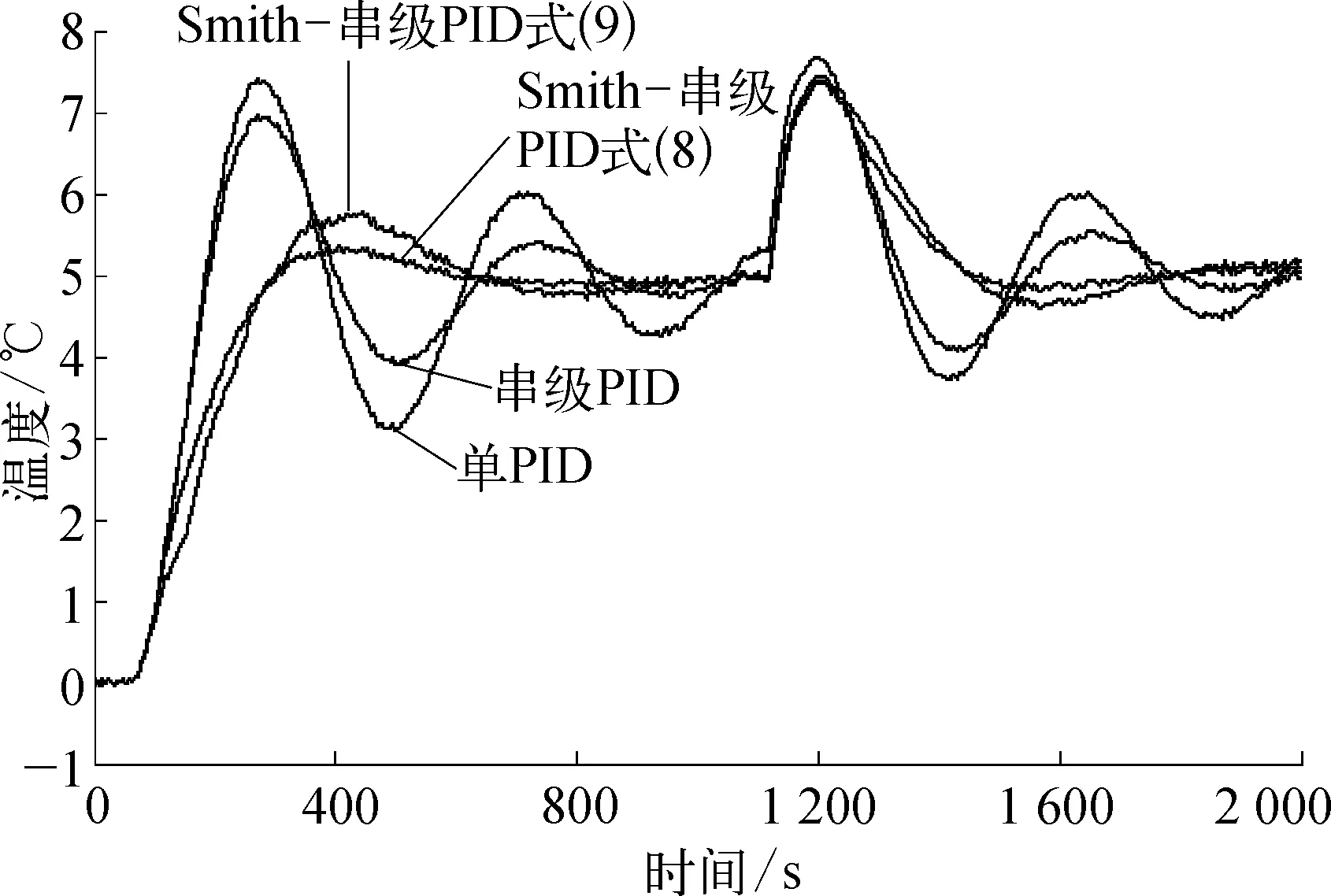
图8　改变一阶响应模型的控制效果比较示意

4.3.4改变放大系数和一阶延时时间

在三种控制方式下，分别修改了Smith预估模型的放大系数和一阶延时时间，预估模型如式(10)、式(11)所示，其仿真结果如图9所示，发现延时时间降低至20s时，控制量略微上扬，而延时时间增加至70s时，系统发生了持续震荡情况，经多次仿真，只要模型的延时时间不大于实际响应时间的30%，均会取得较好的效果。

(10)

(11)

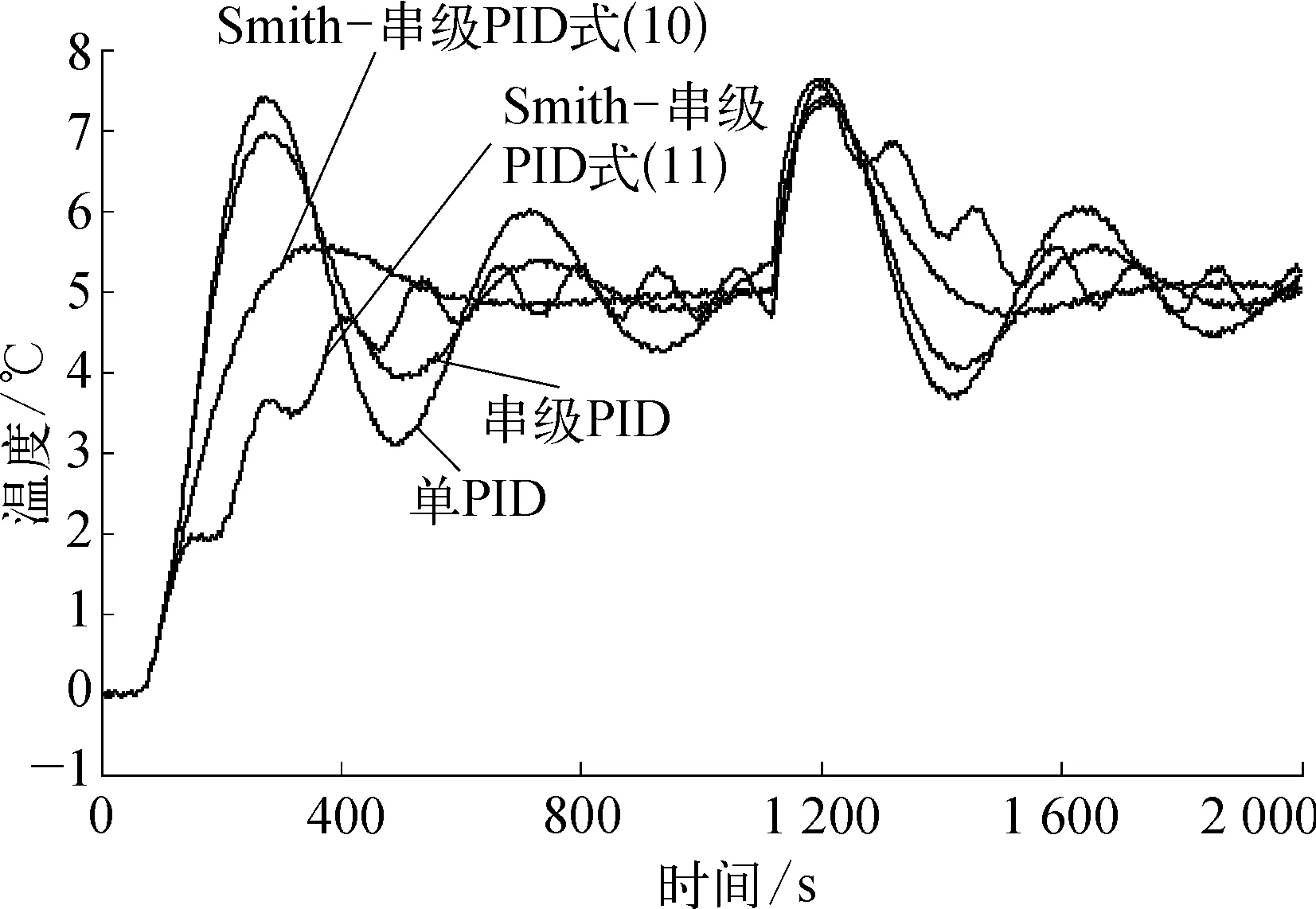
图9　改变放大系数和一阶延时模型控制效果比较示意

由以上四种情况可知，系统的传递模型变化、放大系数不大于实际模型的200%(动态响应时间延长)、延时时间不大于实际响应时间的30%，对于锅炉控制模型均可以取得比单PID和串级PID好的控制效果。因此，该Smith-串级PID控制只要延时时间适当、利用DCS的一阶辨识模型是可以满足现场实际需要的。

5Smith-串级PID控制的实际应用

某厂DCS为艾默生的Ovation3.0.4版本的集散控制系统，其锅炉部分有2对冗余的OCR400控制器，控制器内分为5个任务区，分别为task1/2/3/4/5区，1/2区为快速响应区，3/4/5区为1s扫描周期区域，该控制系统的组态逻辑为模块化结构，组态逻辑图的控制算法只有PID和分段PID，均为增量式PID的算法以及一些其他的逻辑搭接块构成。为了在Ovation3.0.4版本系统中实现Smith-串级PID控制，利用Leadlag模块和Transport模块以及SUM模块进行了搭接，实现了Smith预估控制器的功能。

5.1DCS主要模块说明

5.1.1Leadlag模块

Laedlag是非线性超前/滞后函数，其输出值是旧输出、旧输入、新输出、增益、超前和滞后时间常数的函数。在稳定状态，OUT=IN1.GAIN；输出达到5个时间常数中的期望稳定状态-输出值的98%，也可将其配置成纯超前函数，为稳定状态输出值的98%，并将非线性超前/滞后函数各参数进行设置，实现需要的函数。

5.1.2Transport模块

Transport算法是采样模拟量输入点，并输出带有延时的样本值。采用时间和样本数控制延时；如果采用时间小于Transport的回路时间，则样本数等于回路时间；输出为0直至收集到足够数量的样本。样本数限制在1～25，并将采样模拟量输入点各参数进行设置，实现需要的函数。

5.2Smith控制逻辑搭接以及参数配置

利用PID模块、Input模块、Output模块、Plot模块、Transport模块、SUM模块、Setpoint模块、M/A Station模块、Mode模块、Leadlag模块进行搭接。

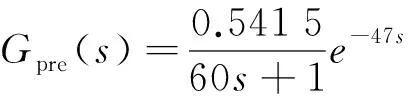
在Ovation的DCS中，实现Smith预估-串级PID控制，经调试后，目前运行良好，实现了主蒸汽温度的高品质控制，其控制效果如图10，图11所示。

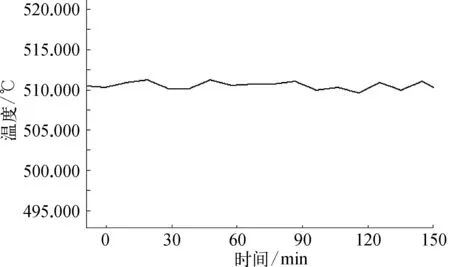
图10　屏翼过热器出口温度3h运行曲线示意

图11　主蒸汽温度3h运行曲线示意

6结束语

CFB锅炉主蒸汽温度控制系统具有大滞后、非线性的特点，采用单PID和串级PID控制方式很难达到满意的控制效果。笔者利用离线辨识以及Matlab仿真的方法，证明了Smith-串级PID控制在预估模型适配度不高的情况下，是可以实现优于单PID和串级PID控制效果的，且控制算法简单、计算量小、易于实现。因此，笔者将该控制方式运用在了Ovation 3.0.4的集散控制系统中的锅炉主蒸汽温度控制上，取得了较好的控制效果。

参考文献:

[1]徐军，吴锡生.锅炉主蒸汽温度控制研究[J].化工自动化及仪表,2004(05)： 56-58.

[2]刘金琨，沈晓蓉，赵龙.系统辨识理论及Matlab仿真[M].北京： 电子工业出版社,2013.

[3]李言俊，张科．系统辨识理论及应用[M]．北京： 国防工业出版社，2003．

[4]杜锋,杜文才.基于新型Smith预估补偿的网络控制系统[M].北京： 科学出版社,2012.

[5]周以琳，戚淑芬.一种改进的Smith预估补偿方案在生产过程控制中的应用[J].石油化工自动化，2000，36(04)： 21-23.

[6]朱晓东，王军，万红.基于Smith预估的纯滞后系统的控制[J].郑州大学学报： 工学版，2004(01)： 77-81.

[7]王燕，杨平.主汽温控制系统MCP-PID控制[J].石油化工自动化，2014，50(05)： 34-37.

[8]高思,康静秋,杨振勇.基于递推最小二乘法的主蒸汽温度控制系统辨识与优化[J].热力发电，2011(06)： 29-33.

[9]韩璞,袁世通,张金营.超超临界锅炉主汽温控制系统的建模研究[J].计算机仿真，2013(12)： 115-120.

[10]齐晓慧，田庆民，董海瑞.基于Matlab系统辨识工具箱的系统建模[J].软件开发与应用，2006,25(10)： 88-90.

Applications of Smith Cascade of PID on Main Steam Temperature Control of Boiler

Feng Huishan

(Sinopec Tianjin Petrochemical Co. Ltd., Tianjin,300271, China)

Abstract：Focusing on problems of large delay, nonlinear for main steam temperature, traditional PID control can not meet requirement of high precision control and there is lack of advanced control methods in current used system. Forecast model is still better than PID control even under large deviation through matching degree of Simth forecast and Matlab simulation application. Load rate of controller will not be increased with introduction of forecasts. CFB boiler main steam temperature control is realized with connecting Simth forecast to existing algorithm package in DCS with combining cascade PID control. Better results have been achieved.

Key words:main steam temperature; boiler; PID control; Smith estimation

作者简介：冯慧山(1963—)，男，毕业于抚顺石油学院生产过程自动化专业，获学士学位，主要从事生产过程仪表设备管理工作，任高级工程师。

中图分类号：TP273

文献标志码：B

文章编号：1007-7324(2016)03-0041-05

稿件收到日期： 2016-03-04。