基于MLD的加权区间预测控制

戚龙欣，王宇红

(中国石油大学(华东) 信息与控制工程学院，山东 青岛 266580)



基于MLD的加权区间预测控制

戚龙欣，王宇红

(中国石油大学(华东) 信息与控制工程学院，山东 青岛 266580)

摘要：针对生产过程中某些被控变量并没有苛刻的设定值要求，只要满足在给定区间内即可的问题，提出了一种基于混合逻辑动态模型的加权区间预测控制算法，在控制器设计中引入逻辑变量，将基于逻辑命题的目标函数以约束条件的形式集成到预测控制器模型框架下。通过逻辑变量的取值检测被控变量预测值所处的偏差区域，设定相应的误差权重值，使预测控制根据输出在不同的偏差区域范围，采取不同的控制强度，从而保证快速控制的同时满足稳定控制的要求。通过对Shell塔的仿真，验证了算法的有效性。

关键词：混合逻辑动态预测控制偏差区域权重

生产过程控制中，控制目标一般为给定值控制，随着现代工业的不断发展，控制要求不再是严格的跟踪给定值，而是只要满足一定的期望区间即可，即区间控制[1]。模型预测控制(MPC)具有对模型要求低、控制效果好且可以处理约束等优点，广泛应用于现代工业过程控制领域[2-3]。模型预测控制的可处理约束、滚动优化等特征为区间控制的实现提供了基础[4]。文献[4]描述了利用软约束方法，实现区间预测控制。文献[5]将输出目标定义为“漏斗”形状，在此基础上采用MPC方法进行控制。文献[6]采用混合逻辑动态系统(MLD)模型，在控制器设计过程中引入逻辑变量，将基于逻辑命题的目标函数转换成混合逻辑不等式，并将其集成在预测控制优化框架下，但其对偏差的处理较简单，被控变量测量值在期望区间外，则取期望区间的中心值作为给定点，按常规给定值控制，测量值在约束区间内，则偏差为零，相应的误差权重值取零，由于环境等干扰的影响，可能会使被控变量在约束区间内震荡。同时，取期望区间的上下限的平均值作为设定值，很有可能将被控变量推向区间控制的某一个边界，在干扰的影响下，超出期望区间，加大控制器的作用频率[7]。

文中首先介绍了MLD模型，然后在文献[6]的基础上，将预测值与给定区间值之间的偏差分为小偏差区域、中偏差区域和大偏差区域。根据偏差区域设定相对应的误差加权矩阵，通过逻辑变量的值检测被控系统预测输出所在的偏差区域，构成基于混合逻辑动态的加权区间预测控制算法，使系统的输出能够快速地回到期望区间内。通过对壳牌(Shell)塔的仿真，验证了算法的有效性。

1混合逻辑动态系统

MLD是由相互作用的连续部分和离散、逻辑部分组成，将被控对象的物理规律、逻辑规则以及输入输出需要满足的约束条件通过命题逻辑转换知识转换成混合逻辑线性不等式约束,集成在模型框架下[8]。

MLD模型的一般形式[9]：

(1)

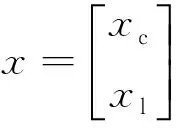
2基于MLD的加权区间预测控制算法

2.1区间控制的MLD形式建模

区间控制可以用图1表示，横坐标表示时间，纵坐标表示输出变量。区间控制一般是应用于多变量系统，为了描述简单易懂，图1中假设只有1个输出变量y1是给定区间控制，剩余输出变量是一般的给定值控制。

如图1中所示，区间控制也就是使区间被控变量不超出给定的期望区间[yC-～yC+]。当yC-=yC+时，区间控制就变成了常规给定值控制[7]。

取期望区间的上下限的平均值为基准点，将区间分为5个区域，分别为负大偏差区域、负中偏差区域、小偏差区域、正中偏差区域、正大偏差区域，见表1所列。

图1　区间控制示意

范 围偏差区域划分控制区划分yB+～yC+正大偏差区域yA+～yB+正中偏差区域控制区yA-～yA+小偏差区域非控制区yB-～yA-负中偏差区域yC-～yB-负大偏差区域控制区

小偏差区域为非控制区，中偏差区域和大偏差区域为控制区，即被控变量在区间[yA-～yA+]内时，控制器不作调整，超出区间[yA-～yA+]，控制器才采取相应的动作。

要完成区间控制目标，首先需要在预测控制中检测输出是否在期望区间内，通过逻辑变量的取值来确定被控变量所在的偏差区域范围。假设1个多变量系统，输出变量y1为给定区间控制，剩余输出变量为常规的给定值控制，则区间控制的MLD形式建模过程如下所示：

1) 在K时刻定义逻辑变量δA-和δA+，用来表示y1所在的区间范围。满足逻辑关系[δA+(k)=1]↔[y1(k)-y1A+≤0]，[δA-(k)=1]↔[y1A--y1(k)≤0]，通过命题逻辑转换知识：

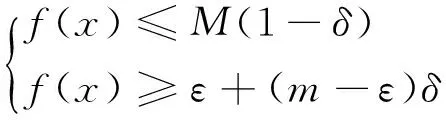
(2)

式中： M=max[f(x)]；m=min[f(x)]；ε——1无穷小的正数[10]。

[δA+(k)=1]↔[y1(k)-y1A+≤0]可以转换成如下不等式：

(3)

同理，[δA-=1]↔[y1A--y1≤0]可以转换成如下不等式：

(4)

2) 设逻辑变量δz融合以上2个信息，δz(k)=δA-(k)δA+(k)，可转换成如下不等式：

(5)

δz=1，表示被控变量进入小偏差区域[yA-～yA+]内，为非控制区。δz=0，表示被控变量进入控制区。

3) 定义辅助连续变量z：

z(k)=(1-δz(k))(y1(k)-y1O(k))=

(6)

式中： y1O(k)——输出y1的期望区间的中间值。

利用命题逻辑转换知识进一步转换成如下混合逻辑不等式约束条件：

(7)

式中： Mz=max(y1(k)-y1O(k))；mz=min(y1(k)-y1O(k))。

4) 定义逻辑变量δB-和δB+作为y1的区域标志(原理同上)，判别y1是否进入中偏差区域。满足逻辑关系[δB+(k)=1]↔[y1(k)-y1B+≤0],得到不等式组：

(8)

满足逻辑关系[δB-(k)=1]↔[y1B--y1(k)≤0]，得到不等式组：

(9)

5) 定义逻辑变量δC-和δC+作为y1的区域标志(原理同上)，判别y1是否进入大偏差区域，原理与上述完全相同。

通过以上定义的逻辑指示变量δ的取值，便可以得到区间被控变量所在的偏差区间范围，控制器采取相应的控制作用。最终，区间控制问题可以表示成MLD的形式进行分析求解。对于多变量系统中存在多个输出变量采用区间控制的情况，原理相同，可由上述推广得到。

2.2基于加权的区间预测控制

基于MLD的加权区间预测控制性能指标为

(10)

受到的约束为

式中：yrj——输出变量yj的期望值；j≠x——输出变量yx为区间控制。

基于加权的区间预测控制，就是指区域被控变量预测值在不同的偏差区域内，相应的权重值取值不同，对应于式(10)中的权重Q2(i)。通过逻辑指示变量δ的取值，可以检测区域被控变量预测值所处的区间范围。

1) 如果区域被控变量在小偏差区域[yA-～yA+]内时，不考虑输出在此区间的变化，相应权重值取为0，即Q2(i)=0，

2) 如果被控变量的预测值在中偏差区域[yA+～yB+]和[yB-～yA-]内，加权系数应随其离小偏差区域越远而增大。

3) 如果被控变量的预测值在大偏差区域[yB+～yC+]和[yC-～yB+]内，其加权系数应达到最大。超出设定的期望区间后就按常规的给定值控制。

被控变量超出期望区间后按常规给定值控制时,权重的取值假设为Q2，Q2的具体值是根据实际生产过程情况进行选取的，对于不同的被控生产对象，取值不同，在本文中取Q2=1。

根据输出预测值所处的偏差区域的不同，相应的权重值函数Q2(i)的取值如下：

(11)

由于控制性能指标中既含有连续变量又含有逻辑变量，导致优化问题是一个混合整数二次规划问题，可通过转换成标准的混合整数二次规划(MIQP)问题求解[10]。

3仿真研究

Shell公司的重油分馏塔过程控制问题是一个标准问题[11]，Shell塔过程模型为

约束为

-0.5≤ui≤0.5i=1,2,3

-0.5≤yj≤0.5j=1,2,3

系统被控目标：y1为区间控制，控制在[-0.1,0.1]；y2为给定点控制，保持在0.2；y3为给定点控制，保持在-0.3。

取预测时域P=10，控制时域M=4，被控变量权系数分别为1,3,2，操纵变量的权系数分别为1,1,1。按文献[6]方法的仿真结果如图2所示。

按照本文的控制算法，根据区间被控变量y1所处的偏差区域的不同，改变y1的相应误差权重值，其他参数相同的情况下，得到的仿真效果如图3所示。

图2　文献[6]算法的区间控制仿真示意

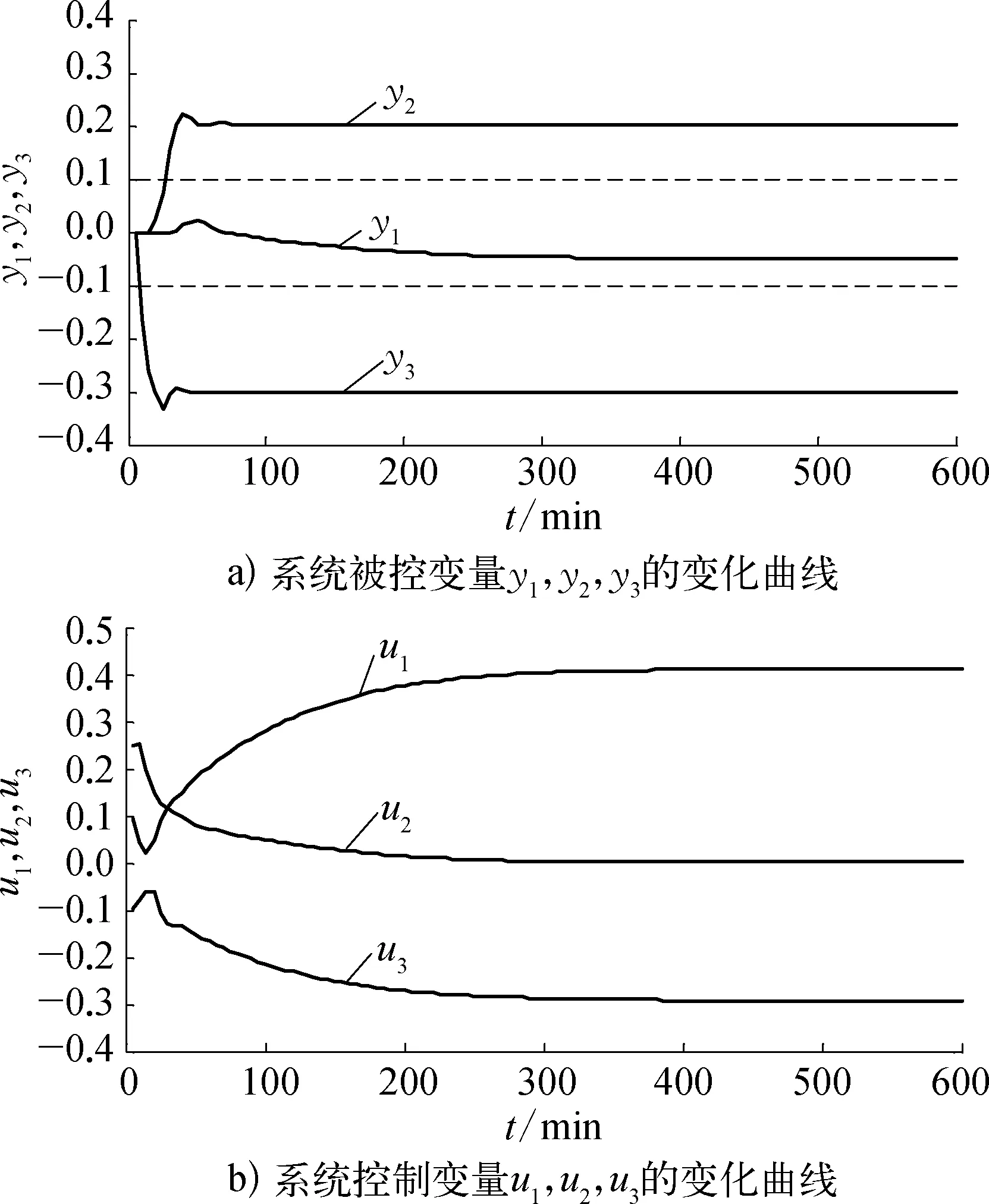
图3　本文算法的区间控制仿真示意

从图2a)和图3a)可以看出文献[6]和本文控制算法均可满足控制要求，但文献[6]的控制算法将区间被控变量y1控制在区间的边界上，很容易在干扰的作用下使得被控变量超出区间范围。而本文的控制算法使y1稳定在区间范围内，而不处于区间的边界，同时y2和y3也实现了定值控制。

为了进一步验证本文算法的可行性，在t=200min时给系统一个阶跃扰动d=0.2，仿真结果如图4，图5所示。

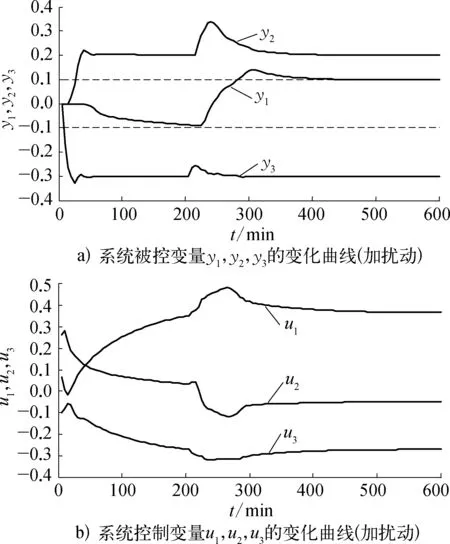
图4　文献[6]算法的区间控制仿真示意(加扰动)

图5　本文算法的区间控制仿真示意(加扰动)

对比图4a)，图5a)可以看出，采用文献[6]的控制算法，系统在第200min受到阶跃扰动后，被控变量y1在区间范围内变化，285min时超出区间范围，然后经过大约115min后稳定在区间范围内。采用本文控制算法，系统在第200min受到阶跃扰动后,被控变量y1在260min时超出区间范围，经过40min后返回到控制区间，返回速度较快，而且最大超调量比未加权的区间预测控制小，增强了系统的抗干扰能力，改善了系统整体的动态性能。

4结论

针对实际工业过程控制中某些被控变量并没有严格的设定值要求，而是只要满足一定的区间范围即可这一特点，笔者提出一种基于混合逻辑动态模型的加权区间预测控制算法，在控制器设计中引入逻辑变量，将基于逻辑命题的目标函数以约束条件的形式集成到预测控制器模型框架下，然后通过逻辑变量的取值检测被控变量预测值所处的偏差区域，设定相应的误差权重值，使预测控制根据输出在不同的偏差区域范围采取不同的控制强度，保证快速控制的同时满足稳定控制的要求。

通过对Shell塔进行仿真，表明本文算法能有效地改善控制性能，实现区间控制的同时，满足控制的快速性和稳定性要求。

参考文献:

[1]罗雄麟，周晓龙，朱丽萍.参考轨迹在线优化的区间预测控制[J].控制工程,2013,20(02)： 223-226.

[2]李少远.工业过程系统的预测控制[J].控制工程,2010,17(04)： 407-415.

[3]MALDONADO M, DESBIENS A, DEL V R. Potential Use of Model Predictive Control for Optimizing the Column Flotation Process [J]. International Journal of Mineral Processing, 2009,93(01)： 26-33.

[4]徐祖华,赵均,钱积新.基于软约束方法的区间预测控制[J].机床与液压,2004,12(03)： 106-108.

[5]QIN S J, BADGWELL T A. An Overview of Industrial Model Pr-Edictive Control Technology[C]//5thInternational Conference on Chemical Process Control. America： AlChE, 1996： 232-256.

[6]邹涛，李少远.带有输出区域控制目标特性的多变量预测控制算法[J].控制与决策,2005,20(02)： 203-206.

[7]商富荣.区间预测控制算法研究及稳定性分析[D].青岛： 中国石油大学(华东)，2008.

[8]赵旭.基于MLD模型的混杂预测控制研究[D].青岛： 中国石油大学(华东)，2010.

[9]王宇红，赵旭.基于MLD模型的预测控制可行性与约束优先级研究[J].控制与决策,2010,25(09)： 1389-1392.

[10]BEMPORAD A, MORARI M. Control of Systems Integrating Lo-Gic, Dynamics and Constraints[J].Automation, 1999,35(03)： 407-427.

[11]PRETT D M, MORARI M. The Shell Process Control Workshop[M]. Boston： Butterworths, 1987： 20-31.

MLD Based Weighted Zone Predictive Control

Qi Longxin, Wang Yuhong

(College of Information and Control Engineering, China University of Petroleum(East China), Qingdao, 266580, China)

Abstract：Aiming at the problem of no rigorous set-point request for some controll variables with only satisfaction requirement of a zone control goal for manufacture process, a weighted zone predictive control algorithm based on mixed logical dynamic model is proposed. Logical variables is introduced into controller design with objective function based on logical proposition integrated into framework of predictive controller in form of constraints. Deviation area of controlled variable predictive value is detected through value of logical variable. Corresponding error weight values are set according to different deviation error range. The predict control takes different control strength to meet requirement of guaranteeing fast and stable control. The effectiveness of proposed algorithm is verified with simulation of shell column.

Key words:mixed logical dynamical; model predictive control; deviation region; weight

基金项目：山东省自然科学基金(2013ZRE28089)。

作者简介：戚龙欣(1991—)，女，在读硕士研究生，从事先进控制理论与技术的研究。

中图分类号：TP273

文献标志码：B

文章编号：1007-7324(2016)03-0036-05

稿件收到日期： 2015-11-12，修改稿收到日期： 2016-04-03。