基于并行计算的混沌遗传算法对反导预警雷达部署优化研究

付　鑫，张　峰，冯占林

(中国电子科学研究院，北京　100041)



工程与应用

基于并行计算的混沌遗传算法对反导预警雷达部署优化研究

付鑫，张峰，冯占林

(中国电子科学研究院，北京100041)

摘要：提出一种高效率的基于MPI(Message Passing Interface)环境的并行混沌遗传算法，求解反导预警场景下的雷达部署优化问题，实现对弹道导弹从被发现到连续跟踪的早期预警。利用分布式并行计算的思想，代替传统串行计算，使算法效率提高7-8倍；为了避免出现"早熟"现象，引入混沌序列对某一代群体中的个体加混沌扰动来提高种群的多样性，并给出了并行计算的混沌遗传算法处理流程。仿真实例表明该算法能够快速得出优化部署方案，时间复杂度降低，大大提高了算法效率，对反导预警雷达部署有较大的应用价值。

关键词：反导预警雷达；优化部署；混沌；遗传算法；并行计算中图分类号：E956

文献标识码：A

文章编号：1673-5692(2016)03-276-07

0引言

随着弹道导弹技术的不断发展，反导系统在各国战略部署中的作用不断突显出来，通过分析国外反导雷达的部署情况对掌握其预警探测能力有重要的军事意义。可见，反导雷达部署方式的合理与否和其探测性能的好坏直接关系到反导预警雷达系统作战效能。寻找一种最佳的雷达部署方案是一个多约束条件多目标组合的优化求解问题。本文将雷达部署位置和阵面朝向作为优化对象，最大发挥反导预警雷达系统作战效能以实现对弹道导弹的早期预警和连续跟踪，文献[1]将遗传算法成功应用于反导预警雷达优化部署上来，当待部署雷达和威胁目标较多时，传统遗传算法计算量大，耗时长，运算效率低[2-3]，不利于应用在实时反导攻防场景中。

基于此缺点，本文通过构建MPI环境，将种群内每个个体适应度的串行计算分布到多台服务器上做并行计算，基于预警雷达在探测、跟踪方面的要求，构造效能指标函数，优化每部雷达的部署位置和阵面朝向。不仅大大加快了优化速度，而且避免了全局变量在同时计算多个个体适应度时发生冲突的问题。同时，为了避免陷入局部收敛，引入混沌序列对某一代种群中的个体产生混沌扰动，利用混沌变量的随机性、遍历性[4-5]的特征进行全局优化搜索，能使算法跳出局部最优，提高种群适应度和多样性。

1系统效能评估指标与评估函数建立

1.1系统效能评估指标的选择

影响反导预警雷达系统作战效能[6]的因素很多，靠单一的指标无法全面衡量，需要建立一套评价体系进行作战效能分析与评估。根据反导预警雷达系统的主要任务：在探测初期对来袭目标尽早发现、继而对其进行稳定跟踪并识别、最终引导拦截武器对目标进行拦截。于是雷达优化部署的目的可具体体现在提高雷达探测系统对来袭目标的及时发现能力、稳定跟踪能力及引导拦截能力，即在对雷达进行部署时应遵循早期发现、稳定跟踪、有效支持拦截的原则。以预警时间、稳定跟踪时间占比、火控支持时间三个主要参数最能表征反导预警雷达系统的及时发现能力、稳定跟踪能力和引导拦截能力。

(1)预警时间[7]

预警时间是指预警雷达系统判断来袭目标首点告警时刻到目标落地时刻的总时长。预警时间越长表明雷达系统的及时发现能力越强。实际中用其归一化参数T1表示。

(1)

其中Ts是系统战技指标对预警时间的要求值。

(2)稳定跟踪时间占比PT

稳定跟踪时间占比是指预警雷达系统对威胁目标跟踪的时间占威胁目标从发射到落地总时间的比。该指标越大说明目标处于被监视的状态比重越大，即雷达系统具有对目标的稳定跟踪能力。归一化后用T2表示。

(2)

(3)火控支持时间TF

火控支持时间是指制导雷达生成火控支持信息的首点时刻至威胁目标落地的时间段。该指标越大表明拦截武器对来袭目标进行拦截的能力越强。归一化后用T3表示。

(3)

其中TB是系统战技指标对火控支持时间的要求值。

1.2综合效能评估函数的建立

在设计综合效能评估函数时，必须遵循以下的准则：

(1)对于弹道威胁权重大的弹道，雷达网系统必须对其进行重点探测和跟踪才能使其预警时间等指标值尽可能大；

(2)尽量不要漏掉对每一条弹道的探测；

(3)对于指标权重大的效能指标，在综合效能评估函数中所体现的作用应更大。

对单条弹道的效能评估函数，考虑到不同作战场景和作战任务，以及各效能指标的重要度不同，建立加权系数用来反映不同指标的重要度。预警雷达系统对该弹道的效能值可写为：

(4)

其中T1、T2、T3分别是归一化后的某条弹道的预警时间、稳定跟踪时间占比和火控支持时间，β1、β2、β3分别是三个指标值的权重。且满足β1+β2+β3=1。若在某一作战场景中，要突出某一指标的重要性，可适当增大指标权重的数值。

同样，在一个作战场景中出现多条弹道时，对应的是综合效能评估函数，可定义为：

(5)

其中n是来袭弹道数量，每条弹道权重为wi，每条弹道的预警探测效能为Ei。

1.3数学关系描述

雷达的部署优化是要对雷达部署经度、纬度和朝向三个参数进行优化。以单部雷达对单条弹道的指标为例。

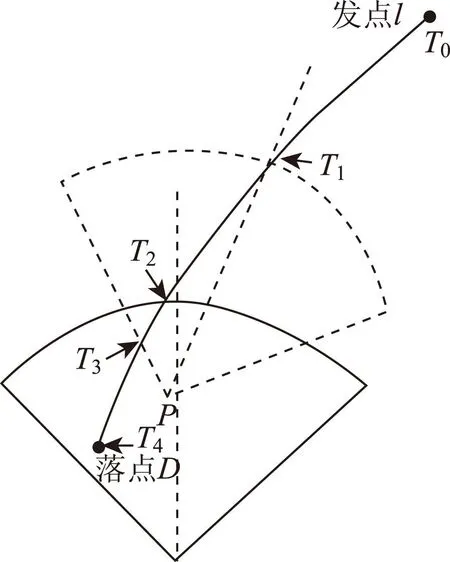
图1　雷达部署与弹道轨迹数学关系

假设威胁目标从点L发射，攻击目标位于D点，运动轨迹如图1所示。假设雷达部署位置为P，雷达阵面朝向为0度，此时来袭目标从T2时刻起至落地均处于雷达探测范围内，雷达对来袭目标的预警效能指标为：

(1)预警时间：TW=T4-T2；

(2)稳定跟踪时间占比：PT=(T4-T2)/(T4-T0)；

(3)假设雷达具有制导功能则雷达的火控支持时间为：TF=T4-T2。

若此时雷达的部署位置从点P变化到P′，阵面朝向顺时针增加θ，则对应的指标参数变为：

(1)预警时间：TW=T4-T1；

(2)稳定跟踪时间占比：PT=(T3-T2)/(T4-T0)；

(3)火控支持时间为：TF=T4-T1。

1.4约束条件

根据本文实际研究情况，将反导预警雷达优化部署问题进行适当简化，作如下约束：

(1)假设待部署雷达可部署的区域是以R为半径的圆形区域内，即优化部署方案中雷达的位置受区域边界的约束；若部署方案中雷达可部署的位置为边界内的海域，则要对目标函数进行惩罚；

(2)假设来袭导弹的发落点位置、弹道数据、威胁权重等参数已知；

(3)假设待部署雷达的性能参数和数量已知；

(4)假设各雷达之间能够进行良好交接；

(5)假设雷达部署不考虑地形因素的影响。

2基于并行计算的混沌遗传算法设计

传统遗传算法缺点是串行计算耗时长，难以满足实时作战仿真过程的要求，为解决这一问题，将计算每一代种群适应度的串行计算分布到多台服务器上进行并行计算。另外，传统遗传算法易陷入局部最优，为防止提前“早熟”现象，利用混沌具有的对初始值的敏感性、遍历性特点，在某一代群体中的个体加入Tent混沌扰动，提高种群适应度，混沌搜索可以对陷入局部极值的个体产生混沌扰动变异，有效跳出局部最优点，保持种群的多样性。

2.1Tent映射

Tent映射又称帐篷映射[8]，是分段线性一维映射。它的形式简单、功率谱密度均匀、相关特性较好，其表达式为：

(6)

当α=2时，称为中心Tent映射，将Tent映射经过贝努利移位变换表示为：

(7)

用随机变量ρ来防止序列进入不动点和小周期，将表达式改写为：

(8)

在随机方程的扰动下，Tent映射能够在达到小周期点或不动点时重新进入混沌状态，增强了遍历性，能更好地实现全局混沌寻优。把x0=0.1作为迭代的初始值，做1 000次迭代运算，能够得到混沌序列{xn}，图2所示改进的Tent映射混沌状态，看出序列分布均匀，能全局遍布各个取值，能够表现出更好的均匀性和随机性。

图2　改进的Tent映射混沌状态

2.2混沌遗传算法设计

首先确定算法与雷达部署优化的参数的对应关系。对于N部待部署的雷达，每部雷达相对于可部署区域中心点的极角、极轴、以及朝向作为染色体上的基因序列，一种雷达部署方案看成是一个染色体，若干个雷达部署方案组成一个种群，需要优化的变量是极角、极轴和朝向，分别用r,θ,O来表示，以最大程度地提高作战效能组合函数为优化目标，获得雷达优化部署方案。若雷达可部署在以(Plon,Plat)为圆心，R为半径的圆形区域内，转换为极坐标形式为(r,θ)，0≤r≤R， 0≤θ≤360°，则雷达部署的经纬度坐标可表示为：

(9)

Step 2 计算适应度。适应度函数是用来衡量群体中各染色体的优良程度。以提高整体作战效能为优化目标，将式(5)作为适应度函数。考虑在实战环境下，地形条件复杂，受阵地环境条件限制不能按照理想形式部署，有时方案会出现部署位置不在陆地，则对该方案进行惩罚，惩罚因子定义为：

(10)

适应度函数调整为：

(11)

Step 3 终止的判断。判断是否符合终止条件，如若符合，算法结束，从种群中找出最优个体；否则，执行Step4。

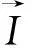
Step 8 对混沌扰动后的向量进行筛选，并计算新的适应度函数值f′，如果混沌扰动后的f′≥f，那么用扰动后的基因序列代替原来的基因序列，否则保留原先的。完成混沌变异过程，得变异后的基因序列。

具体流程图见图3。

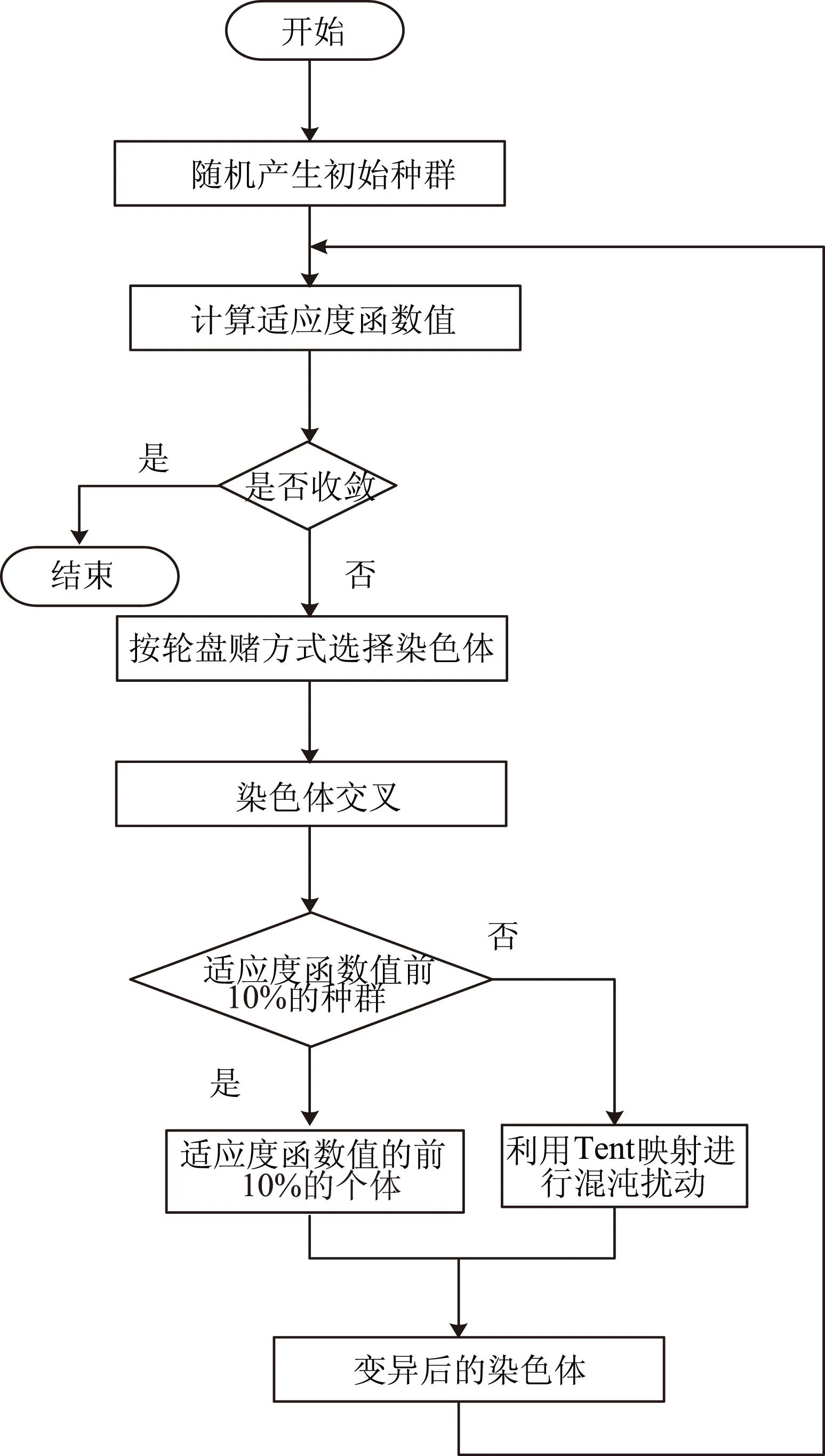
图3　混沌遗传算法流程图

2.3混沌遗传算法的并行处理方案

为了应用并行计算，必须把算法分解成相互独立的若干问题。遗传算法的基本结构及特征决定了它尤其适合大规模并行计算[9-12]。遗传算法中各染色体适应度函数值的求解相互独立，而本算法的设计使得对它的求解占整个计算量的95%以上，若采用主从方式通过构建MPI环境[13-15]实现并行能获得较高的并行度。即由主进程负责初始化和调度各染色体的适应度函数求解，并收集计算结果、控制遗传操作(选择、交叉、变异)、混沌扰动和收敛判断等；而其他从进程接受由主进程发送的染色体，完成适应度函数计算并返回个体适应度值，这样就实现了分布式并行处理的混沌遗传算法。这种主从方式的分布式计算模型实现起来比较方便，并且不需要额外的硬件设施。程序流程图见图4。

图4　基于并行计算的混沌遗传算法流程图

3仿真试验验证与分析

3.1多对一攻击场景

即一个地区受到来自不同方向的导弹攻击威胁(见图5)，弹道参数及威胁权重见表1，其中威胁权重是综合考虑了攻击场景的威胁程度，利用专家打分法获得。若不进行优化部署，利用本文建立的效能评估指标体系求得各个指标值见表2所示。待部署雷达的两种型号A、B具体参数信息如表3。

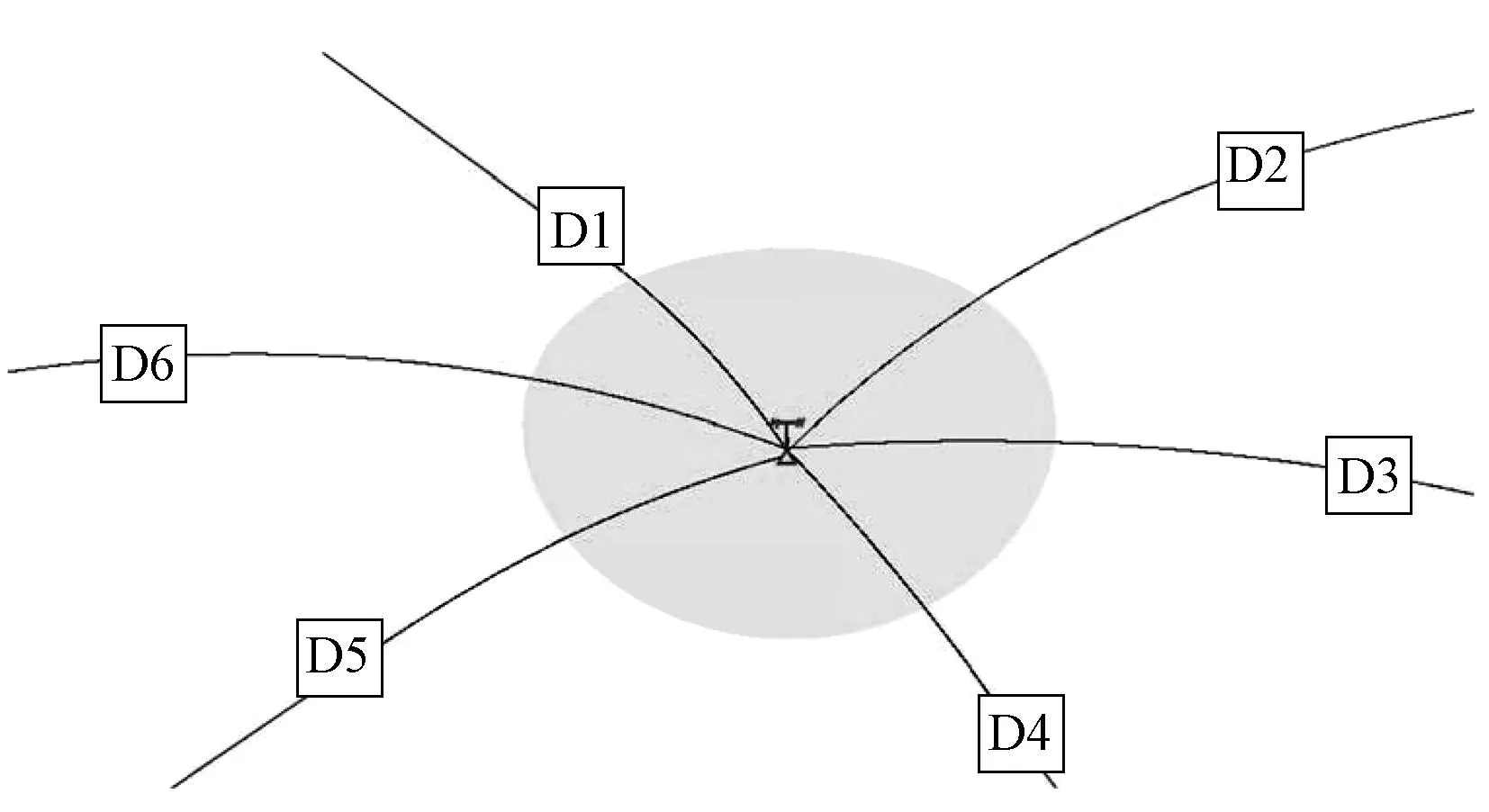
图5　多对一攻击场景

弹道名称发点落点威胁权重D1S1E0.166666D2S2E0.166666D3S3E0.166666D4S4E0.166666D5S5E0.166666D6S6E0.166666

表2　优化前效能评估指标及其权重

表3　待部署雷达参数信息

分别利用传统遗传算法(GA)、基于并行计算的混沌遗传算法(TGA)，对3部雷达进行优化部署，交叉概率为0.8，变异概率为0.05。为了更好的分析和比较两种算法的优化能力和运行时间，在进化代数一定的前提下，将两种算法分别运行10次所用时间和综合指标优化结果对比见表4。图6是两种算法分别迭代800次的目标函数收敛曲线。

表4　两种算法分别运行10次平均优化结果和时间对比

图6　迭代800次的目标函数收敛曲线

优化前效能评估综合指标值为0.746987，从表4看到，利用两种算法优化后的综合效能评估指标值均比优化前得到提高，利用并行的混沌遗传算法优化结果比传统遗传算法优化效果稍微好一些，说明算法的有效性；从平均运行时间结果看到，利用并行的混沌遗传算法运行效率明显提高。从图6看到，传统遗传算法很容易进入局部最优提前收敛，而混沌遗传算法可进行全局优化搜索避免出现“早熟”现象。

3.2多对多攻击场景

即多个地区分别受到来自不同方向的多条弹道攻击威胁(见图7)。E1地区分别受到来自五个方向的弹道攻击，E2和E3地区分别受到来自三个不同方向的威胁攻击，具体弹道参数及威胁权重见表5，假设各个弹道威胁权重相同。若待部署雷达包括A型号两部，B型号三部。分别利用两种算法，对5部雷达进行优化部署。将两种算法分别运行10次比较所用时间和优化结果(见表8)。图8是两种算法分别迭代800次的目标函数收敛曲线。

图7　多对多攻击场景

优化前效能评估综合指标值为0.843983，从表8看到，利用并行的混沌遗传算法优化结果比传统遗传算法优化效果好；而且平均运行时间比传统遗传算法明显缩短。而图8显示，传统遗传算法比混沌遗传算法提前进入局部最优。

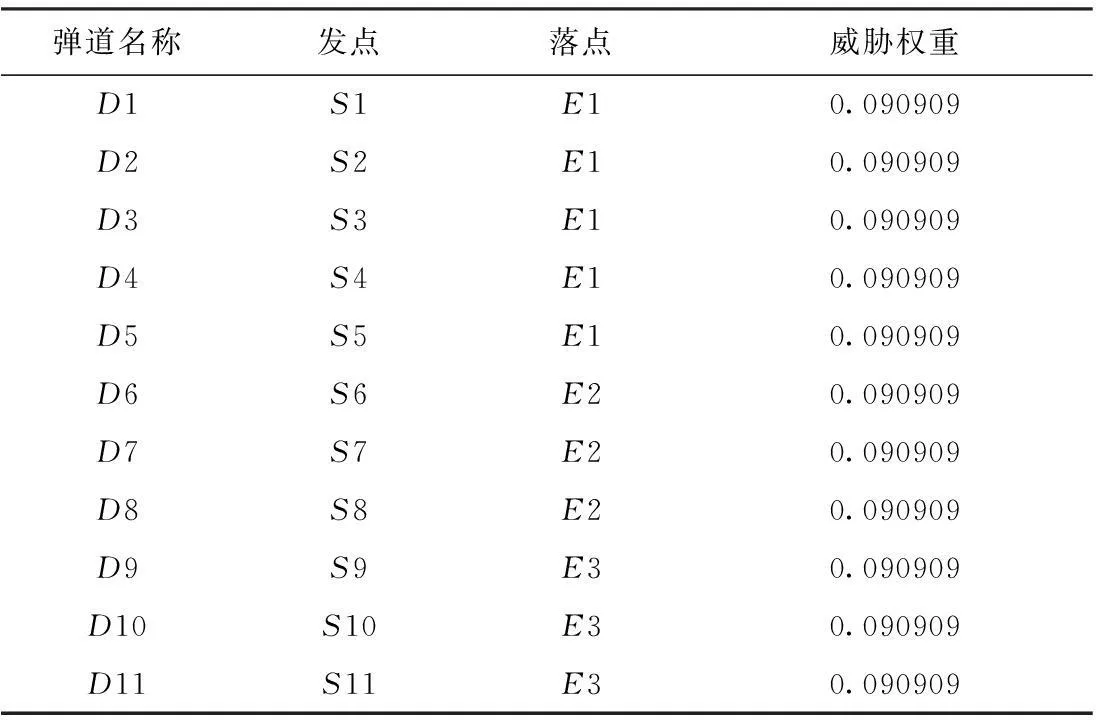
表5　攻击场景弹道参数及威胁权重

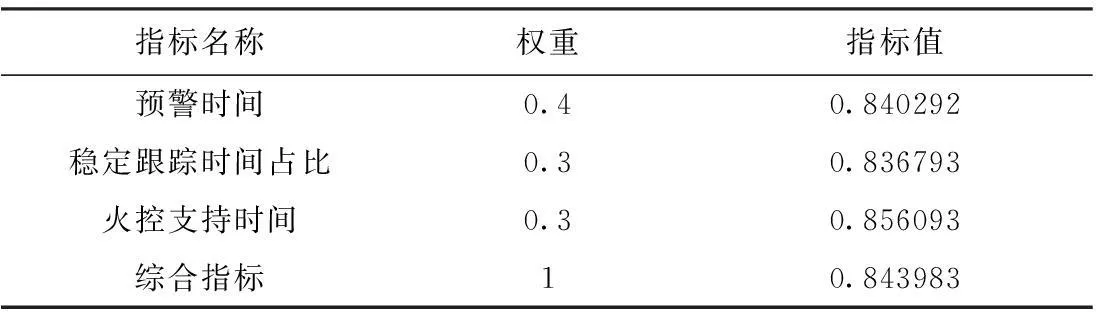
表6　优化前效能评估指标及其权重

表7　待部署雷达参数信息

表8　两种算法分别运行10次平均时间对比

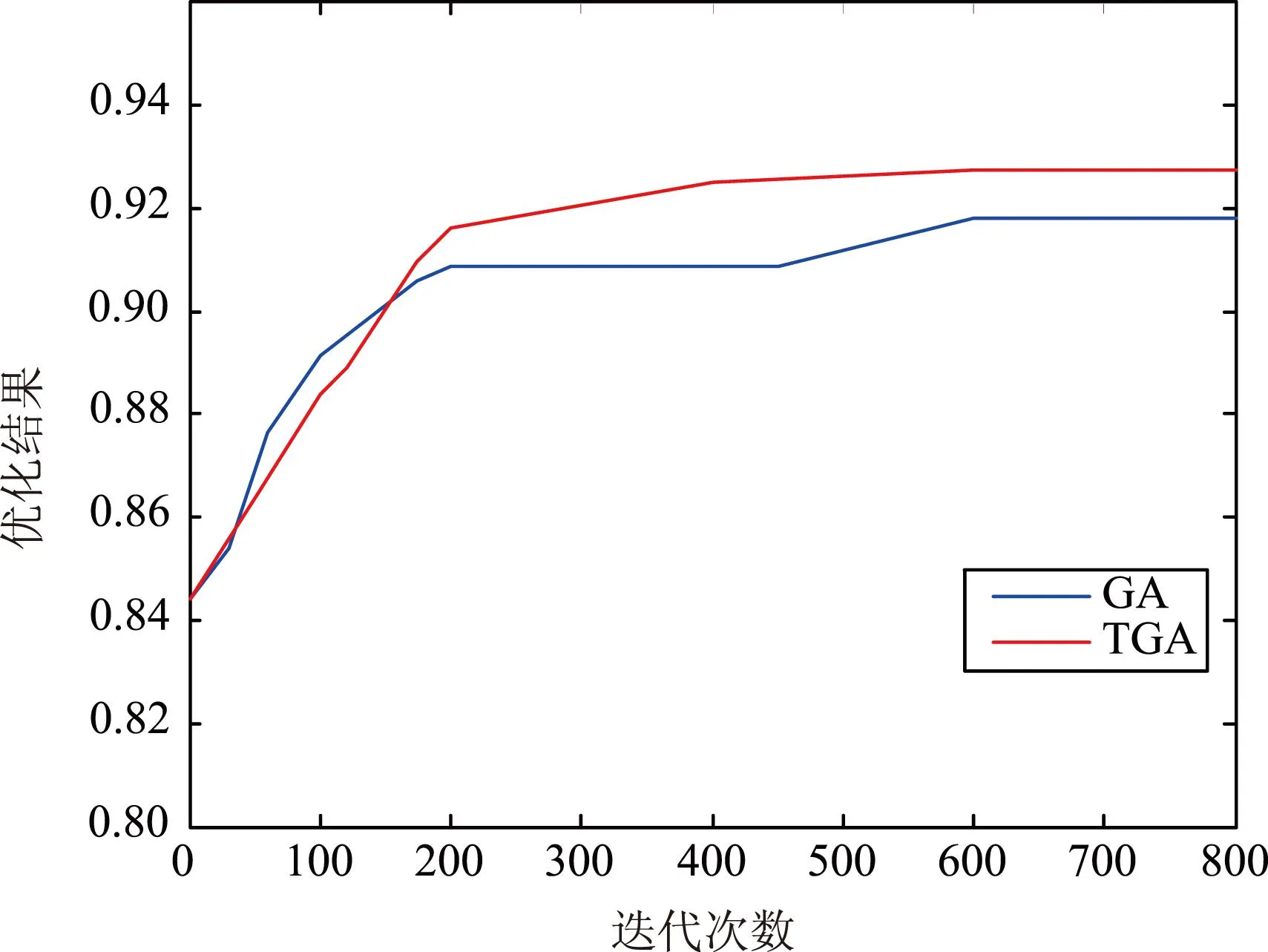
图8　目标函数收敛曲线

3.3仿真结果对比分析

从以上两次仿真实例可以看出，遗传算法容易提早陷入局部最优值，优化结果稍差于混沌遗传算法；并且当迭代相同次数时，基于并行计算的混沌遗传算法的计算效率比传统遗传算法计算效率明显提高7～8倍。因此传统遗传算法不适用于反导系统实时优化部署问题，基于并行计算的混沌遗传算法可以更快的更准确的得到最优值。

4结语

本文针对传统遗传算法耗时长，运算效率低，易出现“早熟”现象的缺点，提出基于并行计算的混沌遗传算法，引入混沌序列并在某一代个体加入混沌扰动，使用变异操作使得问题解能够在全局内进行搜索，通过构建MPI环境实现并行计算的混沌遗传优化。仿真结果表明，经过有限代遗传操作，可以较快的得出雷达部署最优解，并且优化结果良好，明显提高计算效率，对解决反导攻防雷达优化部署问题具有实际意义。

参考文献：

[1]宋佳庆, 张峰, 关永胜, 冯占林, 张晓玲. 基于最优作战效能的雷达部署优化问题研究[J]. 中国电子科学研究院学报, 2015, 4 (10): 372-382.

[2]Fauzi Mohd Johar. A review of Genetic Algorithms and Parallel Genetic Algorithms on Graphics Processing Unit (GPU) [C]. IEEE International Conference on Control System, Computing and Engineering (ICCSCE), 2013, 29: 264-269.

[3]Tomas Potuzak. Sparsely synchronized parallel genetic algorithm for road traffic network division[C]. 8thInternational Conference on Human System Interaction (HSI), 2015: 129-134.

[4]E. N络伦兹著, 刘式达等译. 混沌的本质[M]. 北京: 气象出版社, 1997.

[5]黄润生. 混沌及其应用[M]. 武汉: 武汉大学出版社, 2000. 112-176.

[6]赵新爽, 汪厚祥, 李鸿. 基于SEA法的反导预警系统作战效能评估[J]. 火力与指挥控制，2014, 1(1):157-163.

[7]刘健, 姚澎涛, 罗亮. 早期预警雷达部署要求探讨[J]. 航天控制, 2014, 4(32): 91-96.

[8]Luca, A., Ilyas, A., Vlad, A. Generating random binary sequences using tent map[C]. 10thInternational Symposium on Signals, Circuits and Systems, 2011, pp. 1-4.

[9]吕默, 陈晨, 王一丁. 并行混沌遗传算法在量子级联激光器模型参数优化中的应用[J]. 激光杂志, 2016, 3: 12-15.

[10]Javad Mohammadi, Kamal Mirzaie, Vali Derhami. Parallel genetic algorithm based on GPU for solving quadratic assignment problem[C]. 2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI), 2015, pp. 569-572.

[11]Buhua Chen, Bo Chen, Hongwei Liu, Xuefeng Zhang. A Fast Parallel Genetic Algorithm for Graph Coloring Problem Based on CUDA[C]. International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), 2015: 145-148.

[12]Xin-Yuan Zhang, Yue-jiao Gong, Zhihui Zhan, Wei-Neng Chen, Yun Li, Jun ZHANG. Kuhn-Munkres Parallel Genetic Algorithm for the Set Cover Problem and Its Application to Large-Scale Wireless Sensor Networks[J]. IEEE Transactions on Evolutionary Computation, 2016:1.[13]Robert C. Green, Lingfeng Wang, Mansoor Alam, Chanan Singh. Intelligent and parallel state space pruning for power system reliability analysis using MPI on a multicore platform[C]. IEEE PES on Innovative Smart Grid Technologies (ISGT), 2011: 1-8.

[14]Elias Hadjikyriacou, Nikolaos Samaras. An Experimental Evaluation of a Parallel Genetic AlgorithmUsing MPI[C]. 13thPanhellenic Conference on PCI '09, 2009: 75-79.

[15]Zhurong Wang. A Parallel Genetic Algorithm for Solving the Probabilistic Minimum Spanning Tree Problem[C]. 9thComputational Intelligence and Security (CIS), 2013: 61-65.

Research of Chaos Genetic Algorithm Based on Parallel Computing for Anti-Missile Warning Radar Disposition

FU Xin, ZHANG Feng, FENG Zhan-lin

(China Academy of Electronic and Information Technology, Beijing 100041, China)

Abstract:In view of the disposition of radar detection under anti-missile warning, a high efficiency parallel chaos genetic algorithm based on MPI environment is proposed to achieve early warning for ballistic missile. Traditional serial computing is instead of the distributed parallel computing ideas, which greatly improves the efficiency of operations. The up-time of new algorithm is shortened 70%-80%. To avoid premature, we introduce chaotic sequence to disturb a generation population which increased population diversity. The flow of chaos GA based on parallel computing is described in the paper. Simulation results show that the new algorithm can obtain the best disposition scheme faster. Its performance is superior to the traditional genetic algorithm and greatly improves the efficiency. The algorithm in this paper is important to anti-missile warning radar disposition.

Key words:anti-missile warning radar; disposition optimization; Chaos; GA; Parallel Computing

doi:10.3969/j.issn.1673-5692.2016.03.000

收稿日期：2016-03-15

修订日期：2016-05-05

作者简介

付鑫(1984—)，女，山东聊城人，工程师、博士，主要研究方向为电子信息系统总体设计与仿真；

E-mail: fxzn2006@163.com

张峰(1986—)，男，湖南吉首人，工程师、博士，主要研究方向为电子信息总体设计；

冯占林(1963—)，男，吉林通榆人，研究员、博士，主要研究方向为电子信息系统设计、综合集成、系统分析与评估。