非单调谱投影梯度法求解Toeplitz矩阵的正则化逼近* 1

张雪伟，段雪峰，江祝灵

(桂林电子科技大学 数学与计算科学学院，广西 桂林　541004)



非单调谱投影梯度法求解Toeplitz矩阵的正则化逼近* 1

张雪伟，段雪峰，江祝灵

(桂林电子科技大学 数学与计算科学学院，广西 桂林541004)

摘要：研究Toeplitz矩阵的正则化逼近问题，先利用迹函数的French导数给出目标函数的梯度，再计算任意矩阵到可行集上的投影，最后利用谱投影梯度方法求解Toeplitz矩阵的正则化逼近问题，并用数值例子验证迭代方法的可行性.

关键词：Toeplitz矩阵；正则化逼近；非单调谱投影梯度法

1引言

本文记Rn×n为n×n实矩阵集合,Tn为n×nToeplitz矩阵集合,其元素形如

PΩ(A)为矩阵A在闭凸集Ω上的投影,▽F(X)为函数矩阵F(X)的梯度,tr(X)为矩阵X的迹,‖A‖F为矩阵A的F范数,则有性质‖A‖F=tr(ATA).

本文研究Toeplitz矩阵的正则化逼近问题,即

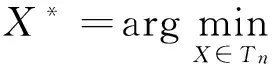
Toeplitz矩阵是一类具有特殊结构的矩阵,它由第一列和第一行的元素确定,且矩阵中与主对角线平行的对角线上的元素相等.Toeplitz矩阵已被广泛的应用于信号处理和图像处理[1-2],工业控制理论[3].对于Toeplitz矩阵逼近问题,其主要工作在于找到一个Toeplitz结构的矩阵来逼近给定的数据矩阵,文献[4-6]提出的一种Toeplitz迭代逼近的方法能很好地解决这一问题,尤其是在计算精度上,但是当矩阵规模较大时,此方法的计算时间较长.J.Murakami[7]提出了一种更加有效的方法来解决大规模问题,相比迭代Toeplitz逼近方法,减少了计算时间,且规模越大计算效率越高.

非单调谱投影梯度法是由文献[8]首先提出的,用来求解形如minf(x),x∈Ω的问题，其中Ω为闭凸集的优化问题.它采用非线性搜索确定步长,并求解出目标函数的梯度和任意矩阵在闭凸集上的投影,然后设计适宜的算法来求解极小化问题.近年来,该方法被大量的研究,详见文献[9-12].

2主要结论

我们先给出目标函数的梯度▽F(X)和矩阵A在闭凸集Tn上的投影,最后利用非单调谱投影梯度方法求解问题I.

下面我们给出矩阵A在闭凸集Tn上的投影PTn(A).

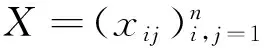
下面给出求解问题I的非单调谱投影梯度算法.算法的初始参数为:初始矩阵X0∈Tn,整数M≥1;小参数αmin>0和大参数αmax>αmin,充分小的参数γ∈(0,1)和参数0<σ1<σ2<1.任意α0∈(αmax,αmin),给定Xk∈Tn和αk∈(αmax,αmin),算法如下:

算法1

步1.检验当前点是否为稳定点. 如果‖PTn(Xk-▽F(X))-Xk‖≤tol，停止，Xk为稳定点.

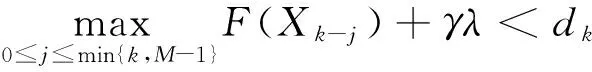
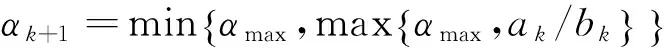
定理2.2由算法2.1产生的迭代序列{Xk}收敛到问题I的解.

3数值实验

所有实验均在MATLAB2009a环境下进行,采用终止条件‖Proj(Xk-▽F(Xk))-Xk‖F<10-10,其中▽F(Xk)为目标函数F(X)在迭代解为Xk时的梯度.由文献[8]可知,当‖Proj(Xk-▽F(Xk))-Xk‖F<10-10时,Xk就是问题I的逼近解.

解的投影残差为‖Proj(Xk-▽F(Xk))-Xk‖F=9.222 2e-16.

例1表明用算法1求解问题I是可行的.

4结束语

本文研究谱投影梯度法求解Toeplitz矩阵的正则化逼近问题.首先,我们考虑问题I，利用矩阵范数的性质计算出其目标函数的梯度,并且由引理1给出了矩阵X在Toeplitz矩阵闭凸集上的投影,然后采用非单调谱投影梯度算法1求解问题I的解.最后给出数值例子验证了此方法的可行性.

参考文献：

[1]R. Chan, M.K. Ng. Conjugate gradient methods for Toeplitz systems[J].SIAM Rev,1996,38:427-482.

[2]M. Hanke, J. Nagy. Restoration of atmospherically blurred images by symmetric indefinite conjugate gradient techniques[J].Inverse Problems,1996,12:157-173.

[3]U. Grenander, G. Szego. Toeplitz Forms and Their Applications[M].New York:2nd Edition, Chelsea:1984.

[4]D. M. Wilkes, M. H. Hayes. Block Toeplitz approximation[J].Signal Processing,1988,15:303-313.

[5]D. M. Wilkes, M. H. Hayes. Iterated Toeplitz approximation of covariance matrices[J].Acoustics Speech, and Signal Processing, 1988. ICASSP-88, 1988 International Conference on. IEEE,1988,3:1663-1666.

[6]J. A. Cadzow, D. M. Wilkes. Enhanced Rational Signal Modeling[J].Signal Processing,1991,25:171-188.

[7]J. Murakami, Y. Tadokoro. A new Toeplitz approximation method for linear prediction matrices[J].Acoustics Speech, and Signal Processing, 1993. ICASSP-93, 1993 International Conference on. IEEE,1993,3:460-463.

[8]E. G. Birgin, J. M. Martinez, M. Raydan. Nonmonotone spectral projected gradient methods on convex sets[J].SIAM J. Optim,2000,10:1196-1211.

[9]E. G. Birgin, J. M. Martinez, M. Raydan. Inexact spectral projected gradient methods on convex sets[J].SIMA J. Numer. Anal,2003,23:539-559.

[10]C. Y. Wang, Q. Liu, X. M. Yang. Convergence properties of nonmonotone spectral projected gradient method[J].J. Comput. Appl. Math,2005,182:51-66.

[11]Z. S. Yu. Solving bound constrained optimization via a new nonmonotone spectral projected gradient method[J].Appl. Numer. Math,2008,58:1340-1348.

[12]S. Bonettini, R. Zanella, L. Zanni. A scaled gradient projected method for constrained image deblurring[J].Inverse Problems,2009,25:002-015.

* 收稿日期：2016-01-20

DOI：10.13698/j.cnki.cn36-1037/c.2016.03.003

基金项目：国家自然科学基金项目(11561015)

作者简介：张雪伟(1990- )，男，河南安阳人，桂林电子科技大学数学与计算科学学院在读硕士，研究方向：数值代数.

中图分类号：O241.6

文献标志码：A

文章编号：1004-8332(2016)03-0011-03

Nonmonotone Spectral Projected Gradient Method for Computing the Regularization Approximation of Toeplitz Matrices

ZHANG Xuewei, DUAN Xuefeng, JIANG Zhuling

(SchoolofMathematicsandComputationalScience,GuilinUniversityofElectronicTechnology,Guilin541004,China)

Abstract:In this paper, we study the problem of the regularization approximation of Toeplitz matrices. We use the French derivative of the trace function to solve the gradient norm of the objective function, then calculate the projection of arbitrary matrix on the feasible set, and design nonmonotone spectral projected gradient method to compute the regularization approximation of the Toeplitz matrix. The numerical examples are tested to illustrate the feasibility of the iterative method.

Key words:toeplitz matrix; regularized approximation; nonmonotone spectral projected gradient method

网络出版地址：http://www.cnki.net/kcms/detail/36.1037.C.20160510.1229.058.html