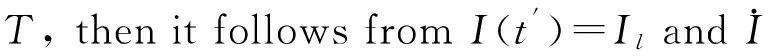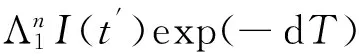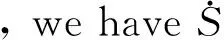A Propagation Model of Computer Virus with Vaccination Strategy* 1

ZENG Jijin, LIU Yujing

(a.School of Business; b.Key Laboratory of Jiangxi Province for Numerical Simulation and Emulation Techniques,Gannan Normal university, Ganzhou 341000, China)



A Propagation Model of Computer Virus with Vaccination Strategy* 1

ZENG Jiajiana, LIU Yujiangb

(a.SchoolofBusiness;b.KeyLaboratoryofJiangxiProvinceforNumericalSimulationandEmulationTechniques,GannanNormaluniversity,Ganzhou341000,China)

Abstract:A mathematical model describing the propagation of computer virus on the Internet is presented, in which continuous control strategy of and impulsive vaccination are taken into consideration. We obtain the reproduction number R0, and further prove that a computer virus cannot invade if R0 is less than unit and can invade if R0 is larger than unit. Several numerical simulations are given to illustrate our main results. Furthermore we find that the combination of continuous and impulsive vaccination is helpful to eliminate the virus.

Key words:computer virus; impulsive vaccination; extinction

1Introduction

More and more applications depend on computer network. Computer viruses attempt to parasitize themselves on a host and spread to other computer through computer network, particularly Internet, damage all kinds of network resources[1].

Due to the high similarity between computer viruses and biological viruses[2], the classical SIR computer virus propagation model was proposed[3]. Since then, more computer virus propagation compartment models have been presented[4-6]. Vaccination is widely regarded as one of the most effective measures of repressing computer virus[4].

This paper aim to investigate the effects of continuous vaccination and impulsive vaccination strategies on the spread of computer viruses and it organize as follows. In Section 2, we formulate the computer virus propagation model. The basic reproduction number is given, followed by an analysis of the model in Sections 3 and 4. The results are illustrated by numerical simulations in Section 5, followed by a discussion of potential further research.

2Model formulation and preliminaries

LetS(t),I(t) andR(t) denote the numbers of susceptible, infected, and recovered nodes in the Internet at timet, respectively. In this section, we propose a propagation model with hybrid vaccination strategy based on [6].

(1)

where

(2)

with initial conditionsS(0+)=S0>0,I(0+)=I0>0.

Lemma 1 IfS(0+)=S0>0 andI(0+)=I0>0, thenS(t)>0 andI(t)>0 for eacht>0.

Lemma 2[7]Let us consider the following linear impulsive system:

(3)

wherea,b>0,0<θ<1. Then there exists a unique positive periodic solution of system (3)

which is globally asymptotically stable.

3The global stability of the virus-free periodic solution

Let us firstly demonstrate the existence of the virus-free periodic solution of system (2). IfI(t)=0 for allt≥0, the dynamic of susceptible individuals must satisfy:

(4)

Theorem 1System (2) always has a virus-free periodic solution (S*(t),0).

In the following, we determine the global attractivity condition of the virus-free periodic solution (S*(t),0). According to[8], we haveF(t)=βS*(t),V(t)=d.LetR0be the basic reproduction number of system (2). Then

(5)

Theorem 2IfR0<1, then the virus-free periodic solution (S*(t),0) of system (2) is globally asymptotically stable.

ProofFirst, we demonstrate that the local stability of the virus-free periodic solution (S*(t),0). LetS(t)=u(t)+S*(t),I(t)=v(t), we get the following linear approximation system of (2) relative to the solution (S*(t),0).

(6)

We can easy obtain the fundamental solution matrix of system (6)

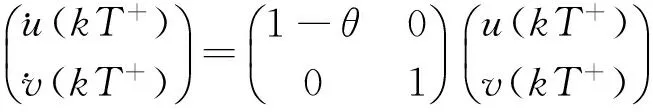
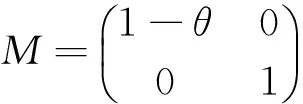
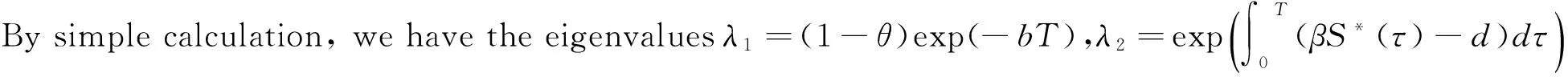
According to the Floquet theory, if |λ2|<1, i.e.R0<1 holds, then (S*(t),0) is locally stable.

In the following, we will prove the global attractivity of the virus-free periodic solution. SinceR0<1, we can chooseε>0 sufficiently small such that

(7)

(8)

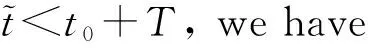
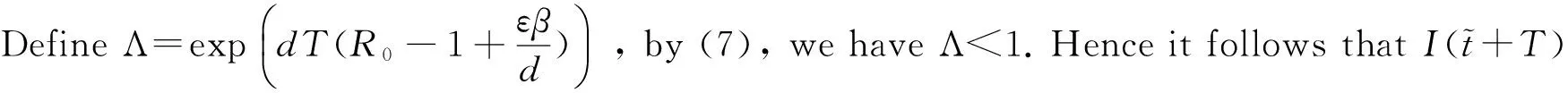
Remark 1Theorem 2 shows that computer viruses will die out ifR0<1.

4Permanence

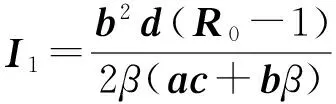
Lemma 3IfR0>1, then for anyt1>0, it is impossible thatI(t)t1.

ProofSuppose that the claim is not valid, thenI(t)t1. SinceR0>1. we can chooseε>0 sufficiently small such that

(9)

(10)

(11)

Integrating the second equation of system (2), by (11) we have

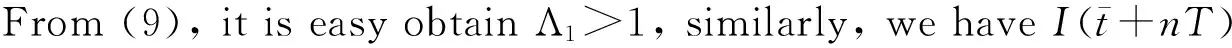
Theorem 3Suppose thatR0>1. Then there is a positive constantηsuch that each positive solution (S(t),I(t)) of system (2) satisfiesI(t)≥ηfor sufficient larget, whereη=Ilexp(-dT).

ProofAccording to Lemma 3, we know that there are left two cases to be discussed.

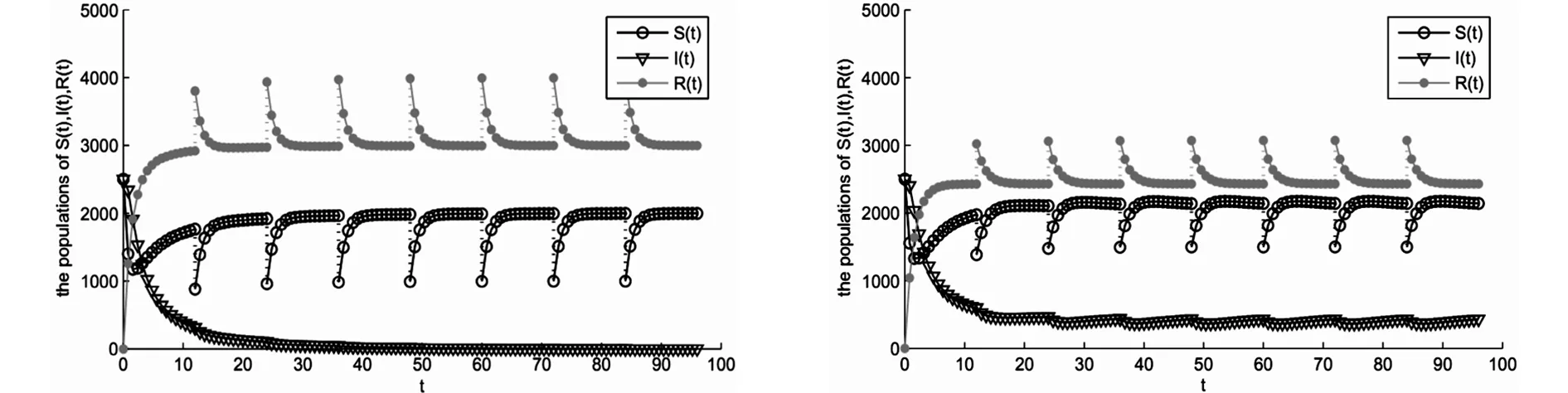
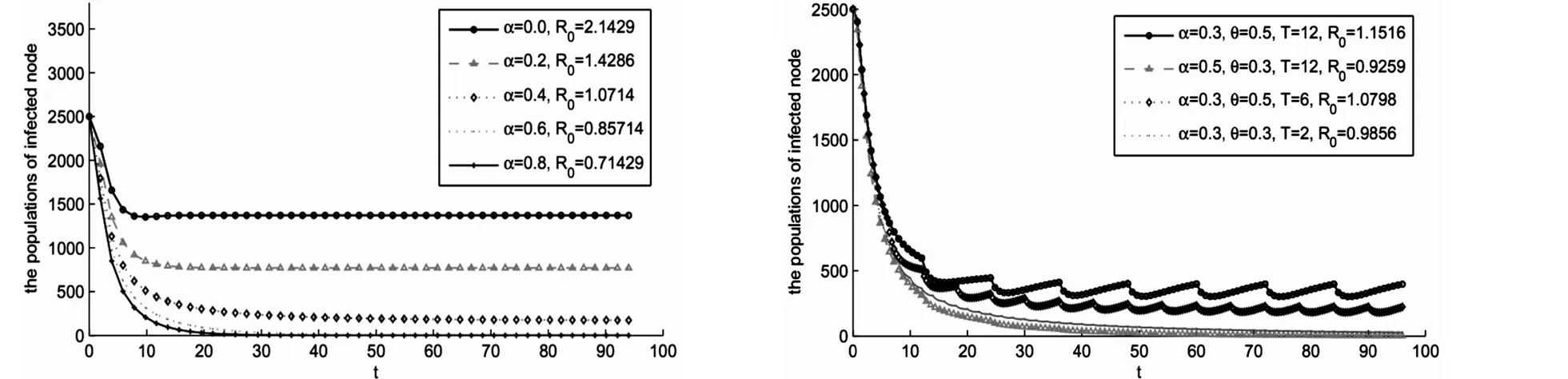
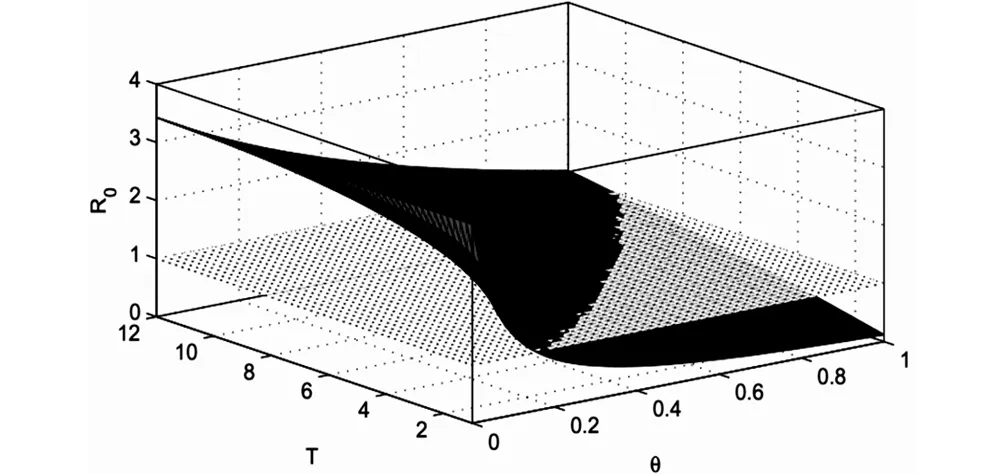
Sett′(>t1) andρ>0 satisfyI(t′)=I(t′+ρ)=IlandI(t)

Case iiIfρ>T, we consider the two cases: A) ift∈(t′,t′+T], the conclusion is evident by Case i;

Since this kind of interval [t′,t′+ρ] is chosen in an arbitrary way (we only needt′to be sufficiently large), we conclude thatI(t)≥ηfor all largetin the second case. In view of our above discussions, the choice ofηis independent of the positive solution of system (2), and we have proved that any solution of system of (2) satisfiesI(t)≥ηfor sufficiently larget.

Theorem 4System (2) is permanent ifR0>1.

By the similar arguments as those in the proof of Theorem 2, we have that there is aε0>0(xsufficient small) such that

(12)

Let Δ0={(S,I)∶Sl≤S,Il≤I,S+I≤N}. From Theorem 3 and inequality (12), we know that the set Δ0is a global attractor in Δ, and then, for every solution of system (2) will eventually enter and remain in region Δ. Therefore, system (2) is permanent. The proof of Theorem 4 is complete.

5Numerical Results

We shall verify the validity of the proposed model through numerical simulation. Consider system (2) with Λ=1 000,γ2=0.2,γ1=0.13,β=0.000 3,α=0.5,μ=0.2,σ=0.3,θ=0.5 andx0=(2 500,2 500,0). AsR0=0.908 3<1, it follows from Theorem 2 that virus-free periodic solution is globally asymptotically stable. Otherwise, change only the parameterαof system (2)α=0.3, thenR0=1.180 8>1. It follows from Theorem 4, that computer virus will persist on the Internet. Fig.1 and Fig.2 show that the computer virus will die out whenR0<1 and will be epidemic whenR0>1, respectively.

Fig.1　Time series of solution for system(2).The virus dies out.　Fig.2　Time series of solution for system(2).The virus is permanent.

To assess the effect of continuous vaccination on controlling the speed of computer virus, we numerically compute the infectious nodes as shown in Fig.3. The increasing of the continuous vaccination rate leads to decreasing the number of infectious nodes, as well asR0. Whenα=0,0.2,0.4,R0>1, the computer virus will be epidemic, meanwhile,α=0.6,0.8,R0>1, the computer virus will die out.

It follows from Fig.4 that, if we fixT=12, continuous vaccination rateα=0.5 and impulsive vaccination rateθ=0.3, virus will die out (R0=0.925 9). Otherwise, continuous vaccination rateα=0.3 and impulsive vaccination rateθ=0.5, virus will be epidemic (R0=1.151 6). But if the impulse-time interval decreases, the final size of virus decreases correspondingly. When the impulse-time intervalT=2, virus will die out (R0=0.985 6).

Fig.3　Time series of I(t) for system (2), 　　　　　Fig.4　Time series of I(t) for system (2), which have different continuous which have different continuous vaccination rate α.　　　　　α and impulsive vaccination rate θ and the impulse-time interval T.

Fig.5 indicates that theR0increases with the increasing of the impulsive vaccination rateθ. Decreasing the impulse-time intervalTleads to a decrease the value ofR0. Especially, if we fix the impulse-time intervalTbelow a threshold value, improving the impulsive vaccination rate simultaneously has effect on the eradication of computer viruses.

Fig.5　The basic reproduction number for system (2), 　which have different impulsive vaccination rate θ and the pulse interval T.

6Conclusion

This paper has studied the long-term behavior of computer virus propagation. An elaborate analysis of the model including the basic reproduction number, the existence of virus-free periodic solution, its global stability and the permanent of the virus has been conducted. It is found that computer virus on the Internet would tend to extinction or permanence according to the value of the basic reproduction number. To illustrate the obtained main results, some numerical simulations have been examined. Our results imply that the combination of continuous and impulsive vaccination is benefit for the inhibition of computer virus spreading.

参考文献：

[1]Denning P. J. Computers under Attack: Intruders, Worms, and Viruses[J].J.Comp 1991,25:134-35.

[2]Kephart J. O., White S. R., Chess D. M. Computers and Epidemiology[J].IEEE Spectrum 1993,30:20-26.

[3]Wierman J. C., Marchette D. J. Modeling Computer Virus Prevalence with a Susceptible-Infected-Susceptible Model with Reintroduction[J].Comput.Stat.Data.Anal 2004,45:3-23.

[4]Data S., Wang H. The Effectiveness of Vaccinations on the Spread of Email-Borne Computer Viruses[C].In: Can.Con.El.Comp.En; 2005:219-23.

[5]Piqueira J. R. C., Araujo V. O. A Modified Epidemiological Model for Computer Viruses[J].Appl.Math.Comput 2009,213:355-60.

[6]Gan C., Yang X., Liu W., Zhu Q. A Propagation Model of Computer Virus with Nonlinear Vaccination Probability[J].Commun. Nonlinear Sci.Numer.Sim. 2014,19:92-100.

[7]Gao S., Liu Y., Nieto J. J., Andrade H. Seasonality and Mixed Vaccination Strategy in an Epidemic Model with Vertical Transmission[J].Math.Comput.Simul 2011,81(9):1855-68.

[8]Wang W., Zhao X.Q. Threshold Dynamics for Compartmental Epidemic Models in Periodic Environments[J].J.Dyn.Differ.Equ 2008,20(3):699-717.

* 收稿日期：2016-03-16

DOI：10.13698/j.cnki.cn36-1037/c.2016.03.002

基金项目：国家自然科学基金项目(11261004)；江西省社会科学规划项目(14XW08)；江西省十二五教育科学规划项目(15ZD3LYB031)

作者简介：曾家健(1975-)，女，广东潮洲人，赣南师范学院商学院副教授，研究方向：区域经济.

中图分类号：O175.1

文献标志码：A

文章编号：1004-8332(2016)03-0006-05

一类具有脉冲控制的计算机病毒传播模型研究

曾家健a，刘于江b

(赣南师范大学 a.商学院；b.江西省数值模拟与仿真技术重点实验室，江西 赣州341000)

摘要：建立一类具有连续和脉冲控制的计算机网络病毒传播模型，得到基本再生数R0，并证明当R0<1时，病毒将消除；当R0>1时，病毒会扩散；数据模拟验证了理论结果.研究结果表明连续和脉冲相结合的控制策略有利于病毒的消除.

关键词：计算机病毒；脉冲接种；灭绝

网络出版地址：http://www.cnki.net/kcms/detail/36.1037.C.20160510.1227.054.html