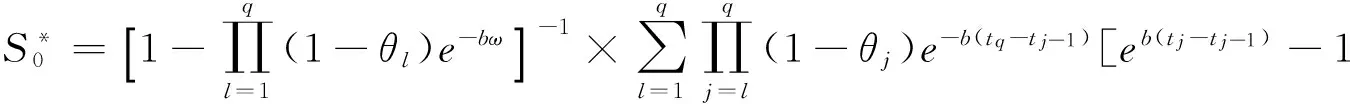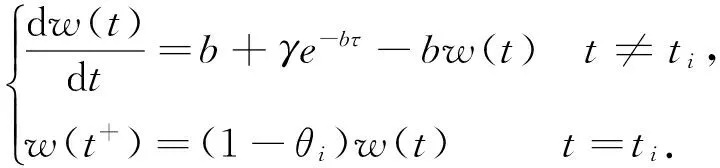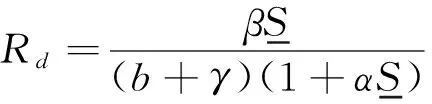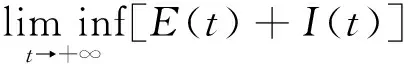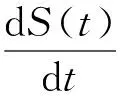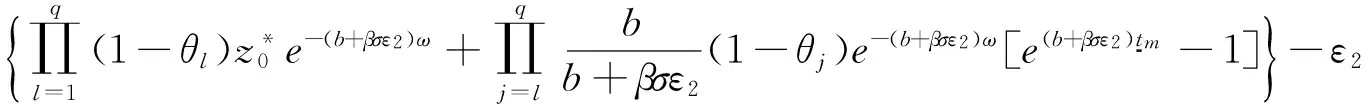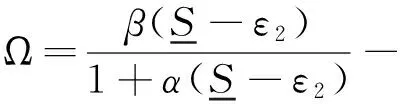一类时变脉冲时滞植物病模型的性态分析* 1

刘　洋，罗友泉，谢飞平

(赣南师范学院 数学与计算机科学学院，江西 赣州　341000)



一类时变脉冲时滞植物病模型的性态分析* 1

刘洋，罗友泉，谢飞平

(赣南师范学院 数学与计算机科学学院，江西 赣州341000)

摘要：建立一类带时滞、时变脉冲的植物病模型，讨论无病周期解的全局吸引性和疾病的持久性，得到两个相应的阈值Rd,Ru，并且证明当Rd<1时，疾病将趋于灭绝，当Ru>1时，疾病将成为地方病.

关键词：时变脉冲;时滞;植物病;吸引;持久

1引言

文献[1]给出了最早的传染病模型-KM仓室模型，在此基础上，生物数学科学工作者做了大量的工作，进行了后续广泛的延拓，取得了丰硕的成果，得到了一系列描述不同传染病传播规律的模型. 利用仓室概念，从简单到复杂又可具体分类为SI模型、SIR模型、SEIR模型、SIRS模型、SEIRS模型等[2]，其中SEIR模型、SIRS模型应用较广泛. 为了适用疾病传播流行的特征，又常对相关模型进行改进，如发生率采用饱和发生率或标准发生率，引入时滞或脉冲，考虑有垂直传染、有暂时免疫等；随着传染病模型的深入研究，现在已将传染病模型思想应用于植物病的传播控制上，如柑橘黄龙病模型[3]、森林病虫害模型[4]，但这方面的文献量相对还是偏少.

作为传染病模型，时滞的考虑往往是因为一个模型系统的演化趋势不仅与当前时刻有关，而且与之前的某些(个)时刻也有关[5]，根据所加时滞的数量，又分单时滞和多时滞问题；而脉冲控制项的加入则是因为有人工干预的出现，如预防接种、喷洒药物、脉冲剔除等等，脉冲控制目前研究较多的是等间隔周期脉冲.关于时滞和脉冲问题的研究已有很多文献可参考，如文献[6-10].

2模型与引理

我们将研究一类具有带时滞和非等间隔周期脉冲的SEIR植物病模型的动力学行为，模型可用(1)式进行描述.

(1)

由于系统(1)的前三个方程与R(t)无关，因此，可将系统(1)简化为系统(2)，后续主要研究系统(2).

(2)

此外，系统(2)满足初值条件：

(3)

引理1[11]设有脉冲微分系统

(4)

其中a≥0，b>0，θi+q=θi，0≤θi≤1,ti+q=ti+ω,ω为正常数，q∈N+，则系统(4)有如下唯一全局渐近稳定的周期正解，当tκ+nω

3系统无病周期解的全局吸引性

记G={(S,E,I,R)∈R4|S>0,E≥0,I≥0,R≥0,S+E+I+R≤1}，显然G为系统(1)的正不变集，下面对系统(2)的讨论将限定在不变集G中进行.

先研究系统(2)无病周期解的存在性.当E(t)=0,I(t)=0时，系统(2)变为

(5)

由引理可知系统(5)存在唯一全局渐近稳定的无病周期正解S*(t)，当tκ+nω

故系统(2)存在无病周期解(S*(t),0,0).下面研究系统该周期解的全局吸引性.

(6)

(7)

(8)

故对于上述ε1，存在k2∈N(k2>k1)，当t≥tk2时，有

(9)

(10)

(11)

根据引理1，系统(10)存在全局渐近稳定的唯一周期正解r*(t)，当tk2≤tκ+mω

同理，系统(11)也存在全局渐近稳定的唯一周期正解u*(t)，当tk2≤tκ+nω≤t≤tκ+1+nω时

4疾病的持久性

定理2若Rd>1，则系统(2)是持久的.

证明因为Rd>1，则存在充分小的ε2>0，使得

(12)

(13)

由系统(2)的第二、第三个式子及(13)可得：

(14)

(15)

下面证明对于所有足够大的t，存在d(0

情形①：对于上述的ε2，当t充分大时均有E(t)+I(t)≥ε2.

情形②：E(t)+I(t)关于ε2振荡.

如果是情形①，结论自然成立.

对于情形②，下面证明也存在d(0

(16)

根据比较原理，在初值条件E(tm)+I(tm)=ε2下，可得系统(16)的解满足

(17)

5总结

本文研究一类非等间隔周期脉冲控制下的植物病模型无病周期解的全局吸引性和系统的持久性，得到了当Ru<1时，疾病将灭绝，当Rd>1时，疾病将成为地方病.显然Ru≤Rd，故文中没有得到疾病流行与否的临界阈值，这将是后续需要做的工作.

参考文献：

[1]Kermack WO, McKendrick AG. Contributions to the mathematical theory of epidemics[J].Proceedings of the Royal Society of London.1927,115(1):700-721.

[2]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2015.

[3]Gao S, Wang J. Threshold Dynamics of a Huanglongbing Model with Logistic Growth in Periodic Environments[J].Hindawi Publishing Corporation Abstract and Applied Analysis.2014,ID:841367.

[4]Wang D, Zhang Y. Stability Analysis of the Forest Insect Pests Model with Time Delays[J].Journal of Biomathematics,2013,28(2):211-219.

[5]张冬梅,俞立.线性时滞系统稳定性分析综述[J].控制与决策,2008,23(8):841-849.

[6]Gao S, Chen L, Nieto JJ, Torres A. Analysis of a delayed epidemic model with pulse vaccination an saturation incidence[J].Vaccine,2006,24:6037-6045.

[7]Wang W, Zhao XQ. Threshold Dynamics for Compartmental Epidemic Models in Periodic Environments[J].Journal of Dynamics & Differential Equations,2008,20(3):699-717.

[8]Yang Y, Xiao Y. Threshold dynamics for compartmental epidemic models with impulses[J].Nonlinear Analysis Real World Applications,2012,13(1):224-234.

[9]Shulgin B, Stone L, Agur Z. Pulse vaccination strategy in the SIR epidemic model[J].Bulletin of Mathematical Biology,1998,60(6):1123-1148

[10]Teng Z，Zhang Y，Gao S. Permanence criteria for general delayed discrete nonautonomous -species Kolmogorov systems and its applications[J].Computers & Mathematics with Applications,2010,59(2):812-828.

[11]Zhang L, Gao S, Xie D, et al. Varying pulse control schemes for citrus huanglongbing epidemic model with general incidence[J].Commun. Math. Biol. Neurosci. 2016:1-13.

* 收稿日期：2016-03-16

DOI：10.13698/j.cnki.cn36-1037/c.2016.03.001

基金项目：国家自然科学基金项目(11561004);江西省研究生创新专项基金项目(YC2015-S375)

作者简介：刘洋(1972-)，男，赣南师范学院数学与计算机科学学院教师，主要从事生物数学方面的研究.

中图分类号：O175

文献标志码：A

文章编号：1004-8332(2016)03-0001-05

Global Dynamics of a Delayed Plant Disease Model with Time-varying Impulsive Control

LIU Yang, LUO Youquan, XIE Feipeng

(SchoolofMathematicsandComputerScience,GannanNormalUniversity,Ganzhou341000,China)

Abstract:In this paper, a plant disease model with time-varying impulsive control and time delay is proposed. Sufficient conditions for global attractivity of disease-free periodic solution and permanence of the system are obtained. If Rd<1, then the disease will die out, and if Ru>1, then the disease will be endemic.

Key words:time-varying impulse; time delay; plant disease; attractivity; permanence

网络出版地址：http://www.cnki.net/kcms/detail/36.1037.C.20160510.1101.002.html