交换超立方网络的(t,k)故障诊断度研究

熊茜，梁家荣，马强

（广西大学计算机与电子信息学院，广西南宁530004）



交换超立方网络的(t,k)故障诊断度研究

熊茜，梁家荣，马强

（广西大学计算机与电子信息学院，广西南宁530004）

摘要：故障诊断是网络系统修复的一个重要环节，PMC诊断模型是一种简单、易于理解的故障诊断模型。通过对以交换超立方网EH（s,p）（1≤s≤p）为拓扑模型的多处理器系统进行结构分析，给出了该网络系统的一般化的故障诊断方法——(t,k)诊断方法，证明了在PMC模型下交换超立方网络EH（s,p）（1≤s≤p）是可诊断的，且是条件可诊断的。结果表明，交换超立方网的(t,k)诊断度大于其传统诊断度s+1，条件(t,k)诊断度大于其传统条件诊断度4s-3。这些结果为交换超立方网络的故障诊断提供了重要的理论依据。

关键词：交换超立方网；(t,k)诊断度；条件(t,k)诊断度；PMC模型

1 引言

随着并行计算系统规模的不断增大，系统中将不可避免地出现故障节点和故障链路，如何有效地识别和定位这些故障节点和故障链路以保证系统的可靠性已成为系统设计、维护工作中的重要部分。在系统中辨别处理器正确与否的过程为故障诊断。当一个故障处理器被识别后，通常用一个正确处理器代替它，以维持系统的可靠性。在多处理器系统中，通过分析有效处理器间的测试结果而识别出故障处理器的过程，称为系统级诊断，这种诊断已被广泛研究[1～7]。系统级故障诊断的基本思想是：系统中的处理器之间相互测试，通过对测试结果进行逻辑分析确定系统中的故障处理器。在系统中能识别出的最大故障节点个数，称为系统的故障诊断度。在系统级故障诊断中PMC故障诊断模型是最常见的一种诊断模型。PMC模型是由Preparata等[8]在1967年提出的，PMC模型诊断的基本方法：对于网络图G(V,E)中任意一条边(u,v)∈E，表示节点u可以测试节点v。当用节点u测试节点v时，节点u称为测试者，节点v称为被测试者，节点u发给节点v一个测试任务，节点v回复一个响应消息。如果响应正确，则记录节点u测试节点v的结果为0，记为σ(u,v)=0；若响应故障，则记录节点u测试节点v的结果为1，记为σ(u,v)=1。一次测试的所有结果的集合称为网络图G(V,E)的一个症状，用σ来表示，它是网络图G(V,E)的边集到｛0,1｝的映射。在PMC模型中，如果一个无故障的节点作为测试者，则它所产生的测试结果是可靠的；如果作为测试者的节点本身发生了故障，那么它所产生的测试结果是不可靠的。

文献[8]介绍了多处理器网络系统的2种故障诊断方法：一步诊断和连续诊断。一步诊断也被称为无修复诊断，关于一步诊断的研究已取得了不少成果，具体可参考文献[9～15]。连续诊断则被称为可修复诊断，用迭代的方式识别故障节点子集，其中，在每次迭代中至少识别出一个故障节点。并且，在一次迭代结束后和下一次迭代开始前，对所有识别出的故障节点需要修复或取代，这个进程一直重复直到所有的故障节点都被修复或取代，可以说连续诊断是一种“分散难度的诊断”。从具体的故障检测而言，一步诊断尽管能一次性诊断出所有的故障节点，然而它对网络连接难度或者说网络的成本开销要求也极高，更多的人们倾向于关注连续诊断。在连续故障诊断研究中，有一种称之为(t,k)诊断的连续诊断（其中，t≥k，系统中的故障节点个数不超过t），它是由Arika和Shibata[16]提出的一种连续诊断的一般化诊断。(t,k)诊断认为，通过迭代的方式对系统中所有故障节点进行识别并修复，在每一次迭代中，(t,k)诊断至少能识别出k个故障节点（或剩余故障节点数小于k时，所有故障节点都将被识别出），相比普通的连续诊断每次至少识别出一个故障节点而言，(t,k)诊断在时间复杂性上有所改善。关于(t,k)诊断已有一些研究成果，如Chen和Hsieh[17]计算并证明了组件网络基于比较模型下的(t,k)诊断度。Chang[18]证明了n-维正则网G是(t,k)可诊断的，当，其中，N为G中节点数，B表示最大故障集合体中的节点数。Chang和Chen证明了d-维网格和圆环面分别是可诊断和可诊断的，其中，N为系统中的节点总数[19]。此外，在传统的故障诊断研究中，所考虑的故障节点是随机分布的，本文称此种故障模式为随机故障模式；然而，有时如果不对故障节点的分布进行限制，会给诊断增加极大的难度，在许多情况下，对故障节点分布做适当的限制，有利于故障节点的识别，同时不会对网络的故障诊断产生太大影响，事实上像“网络中任一节点的邻居节点不全是故障节点的限制”就具有比较客观的意义，例如，对于一个n维超立方体网络，Qn包含个含有n个元素的子集，在这些子集中只有2n个子集包含某些节点的所有邻居，当n足够大时，比率是很小的，即Qn的基数为n的故障集包含任意一个节点所有的邻居节点的概率是很小的。为此，2005年Lai等在文献[20]中提出一种新的故障诊断方法——条件故障诊断。条件诊断假设系统中任何一个节点的所有相邻节点不能同时发生故障，即一个系统中的任何一个节点的所有相邻节点至少有一个是正确的。关于条件故障诊断的研究已取得了一些成果[4,5,9,11,14,21]。

交换超立方网络作为超立方体网络的一种变型网络[22]，有效降低了网络规模增大时所需要的拓扑连接的开销，是一种性能优越的网络。随着交换超立方网络EH(s,p)网络规模和维数的增大，加之网络的高速运行，出现故障节点是不可避免的。如何识别交换超立方网络EH(s,p)的故障节点，进而进行修复，以使该网络能正常通信，是交换超立方网络EH(s,p)面临的重要问题。在交换超立方网络EH(s,p)故障诊断理论研究中，诊断度无疑是一个研究重点，因为诊断度体现了该网络最多能识别的故障节点数的上界，它是故障诊断算法设计与选择的重要基础。目前，关于交换超立方网络的诊断度的研究已取得了一些成果，如文献[23]研究了交换超立方网络悲观一步诊断策略下的诊断度问题，文献[24]研究了交换超立方体网络的超连通度。然而在这些诊断度的算法中，由于每次迭代只能给出一个故障节点进行修复，因而其时间复杂性可达O(2s+p+1)。显然，当交换超立方网络EH（s,p）（1≤s≤p）规模较大时，会给交换超立方网络的故障诊断带来极大的时间开销。为此本文考虑更为广泛意义的连续诊断以及更为实际的条件诊断问题，本文提出2种适用于交换超立方网的基于PMC模型下的诊断方法：(t,k)诊断和条件(t,k)诊断，这2种方法得到的诊断度远远大于其传统诊断度，且在时间复杂性上是传统诊断的。此外，开展交换超立方网络基于PMC模型下的(t,k)诊断度和条件(t,k)诊断度的研究，对丰富和发展交换超立方网络的故障诊断理论具有重要的学术意义，为交换超立方网络运行的可靠性研究提供重要的理论支撑。

2 预备知识

在多处理器系统的研究中，一个系统的基础拓扑结构通常用图G(V,E)表示，其中，任意节点v∈V表示一个处理器，任意边（u,v）∈E表示节点u和v之间的一条通信连接。节点u的邻居表示的是和u互连的任意节点，并用N(u)表示节点u的所有邻居节点集合，即N(u)=｛v|（u,v）∈E｝。对于一个子集U⊆V，N（U）表示的是U中所有节点的邻居节点集合，即有N（U）=∪u∈UN（u）-U，且其在点集W⊆V中的邻居节点集合表示为N（U,W）=｛v|（u,v）∈E,u∈U且v∈W｝。其中，节点u的度表示和u相连边的数目。如果G是一个无向图且图中任意2个节点都是连通的，那么称G为连通图；如果G是一个有向图且满足上述条件，则G是一个强连通图。如果G是非连通的，那么在G中的最大连通子图即为G的连通分支，如果某个连通分支仅含一个节点，称此连通分支为平凡连通分支；否则为非平凡连通分支。从G中移除一个点集S，如果移除节点后的G是非连通的或仅剩一个节点，那么称S可达到的最小基数为图G的连通度，表示为k(G)。系统S的故障节点集即为所有故障节点的集合，它可以是V的任意子集。在PMC模型下的故障诊断的意义如引言所述。

通过引言中对(t,k)诊断的描述，本文给出以下定义。

定义1给定系统S的故障节点集为F，σ为S在F下的任一症状，如果：1）当时，所有故障节点可被识别；2）当时，至少k个故障节点可被识别，那么S就是(t,k)可诊断的。

由定义不难得知，一步诊断和连续诊断是(t,k)诊断的2个特例。当t=k时，(t,k)诊断即为一步诊断；当k=1时，(t,k)诊断为连续诊断。

如果系统S的子集A满足下面2个条件，则可称A为症状σ的可允许故障集。

直观上，A是关于σ的一个可允许故障集，当且仅当A中的节点都是故障的，且不属于A的节点都是正确的，并在此假设下A能产生一个和σ相同的症状。显然，S的故障节点集是关于σ的一个可允许故障集。那么，所有基数不超过t的关于症状σ的可允许故障集的交集就是S的故障节点集的一个子集，即有下列引理。

引理1[16]对于故障节点数不超过t的系统S，给定任意症状σ，

Ψσ,t={F| F 是关于症状σ的一个可允许故障集,且≤t} ，那么S是(t,k)可诊断的当且仅当

下面的内容描述了交换超立方网的定义和相关性质。

定义2[22]交换超立方网是一个无向图EH(s,p)=(V,E)(s≥1,p≥1)。其中，V是节点集。

V={as-1…a0bp-1…b0c| ai,bj,c∈｛0,1｝,其中,i∈［0,s）,j∈［0,p）}；E表示边集。

其中，⊕为异或符号；v［ x: y］表示字符串v从x位到y位的部分字符串；H（x,y）表示节点x到节点y的海明距离，并且（x,y）∈V×V。图1给出交换超立方网的EH(1,1)和EH(1,2)。

引理2[22]EH(s,p)可以分解成2个EH(s-1,p)或EH(s,p-1)。

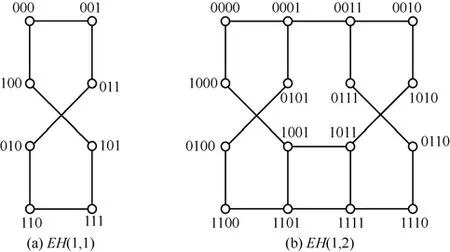
图1 交换超立方网EH(1,1)和EH(1,2)

3 交换超立方网的(t,k)诊断度

本文将使用一个有向图G（V,E）以表示交换超立方网EH(s,p)（1≤s≤p）。假设（u1,u2,…,um）是G中从节点u1到节点um的有向路径，且σ是G对应的一种症状。当σ（ui,ui+1）=0，其中，1≤i≤m-1，那么u1是故障的或u1,u2,…,um都是正确的。使用G+表示G的一个生成子图，其中，所有边（ui,uj）都满足条件，即G+=（V+,E+），其中，V+=V且E+=｛（ui,uj）|（ui,uj）∈E且σ（ui,uj）=0｝。并且使用C表示G+中所有强连通分支的集合。

由于同一强连通分支中的2个不同节点u和v之间，总是存在着一条从u到v的有向路径，所以在C中的每个连通分支的所有节点都是正确或都是故障的。如果一个连通分支中的所有节点都是正确的，则称此连通分支为正确的连通分支；否则称其为故障的连通分支。如果，那么V中所有节点都是正确或都是故障的，这与实际情况不符。所以在此可以得知。将C中任一连通分支当成一个点，对于连通分支X和Y，当节点x∈X、节点y∈Y且存在（x,y）∈E时，那么表明X和Y可通过边（x,y）连接。本文构造图，其中，且如果,N（X）则表示X在中的邻居连通分支的集合，即N（X,W）则表示X在中的邻居连通分支的集合，即

通过上述内容，本文引申出下列几个引理，用于判断连通分支是否正确。

证明由于Y∈N（X），即存在（x,y）∈E,其中，x∈X且y∈Y 。假设X和Y都是正确的，那么X和Y属于同一个连通分支，这与假设不符，所以Y是一个故障的连通分支。

证明如果X是故障的，那么G中故障节点个数将大于或等于t+1，这与假设不符，所以X是正确的连通分支。

Khanna和Fuchs[5]定义了函数Φ用以研究连续诊断。下文中将扩展Φ的定义，使得此函数适用于(t,k)诊断。

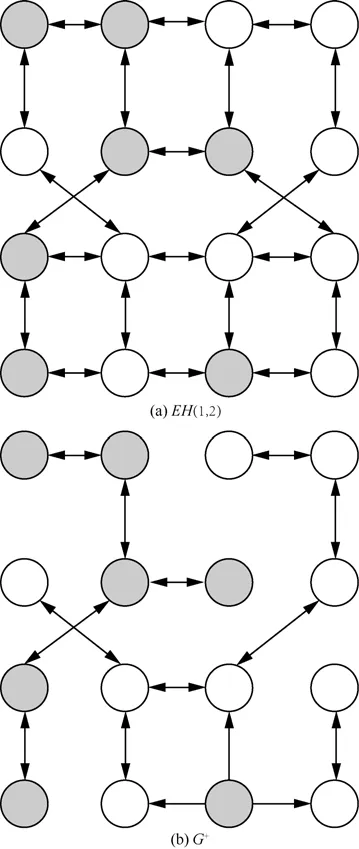
图2 EH(1,2)的图G生成子图G+

通常来说，对于一个给定系统，求出Φ函数是比较困难的。为了将上述的方法能得以实现，本文将寻找满足条件的t值和k值。下节内容求算了交换超立方网EH（s,p）基于PMC模型下满足(t,k)诊断的t值。

3.1 可取的t值

定义I（α）=max|{(z1,z2)|z1∈Z,z2∈Z且，即在基数为α的子集内，计算出端点都在此子集内的边，其中，I（α）为在G中选取不同子集而计算出的最大值。显然I（1）=0。在本文中，假设对数函数以2为底。

引理5 在交换超立方网中，I（α）≤αlbα

证明根据引理2可得，EH（s,p）可拆分成2个EH（s-1,p）或2个EH（s,p-1）。在本节中，将EH（s,p）拆分成2个EH（s-1,p），并记做EHa（s-1,p）和EHb（s-1,p）,将EH（s,p）记做（s+p）维交换超立方网，EH（s-1,p）记为（s+p-1）维交换超立方网。假设X是G的一个子集，即X⊆V，且，其中，设Xa为X与 EHa（s-1,p）的交集，Xb为X与EHb（s-1,p）的交集，即有

在下列内容中，本文将结合交换超立方网的结构性质和上述相关内容，求算出Ψ（t+1）的不等式关系，并根据此不等式关系求算出满足(t,k)诊断的t值，即系统的(t,k)诊断度。

证明假设F=｛Y1,Y2…Yd｝且其中，。在交换超立方网EH（s,p）（1≤s≤p ）中，每个节点的度为s+1或p+1,即所有节点的度都小于或等于p+1。由于与F中任意节点相连的边的数目不超过，其中，为2个端点都在F内的边数，那么就有F与(V-F)之间的边数小于或等于

化解不等式有

下节内容论述了交换超立方网EH（s,p）基于PMC模型下满足(t,k)诊断可取的k值。

3.2 可取的k值

引理8 对于图G=（V,E），如果U是V的一个子集，且W⊂V-U是V-U的一个连通分支，那么

证明 因为W⊂V-U且W是连通分支，所以在W和V-U-W之间不存在任何边。如果，那么W不能成为V-U的一个连通分支，这与假设相矛盾，所以

通过上述求算出可取的t值和k值，且有交换超立方网EH(s,p)(1≤s≤p)的点连通度k(G)=s+1，即可以得出定理1。

由定理1可知，交换超立方网基于PMC模型下的(t,k)诊断度为，而交换超立方网的传统诊断度已知为k(G)，其中，,很显然，所以交换超立方网基于PMC模型下的(t,k)诊断度大于其传统诊断度。

4 交换超立方网的条件(t,k)诊断度

在本节中，将讨论交换超立方网EH(s,p)的条件(t,k)诊断度，即在交换超立方网中的任意一个节点存在至少一个正确邻居节点的限制条件下，对交换超立方网进行(t,k)诊断方法得到的诊断度。和第3节类似，首先将构造出G的生成子图G+，并在G+中划分出各个连通分支。下面介绍几个引理，用以判断某些连通分支是否正确。

引理10 X是G+中的一个连通分支，如果存在节点x∈X且N（x）⊆X，那么X是正确的连通分支。

证明 假设X是故障的连通分支，即节点x是故障节点。由于在G+中E+={(ui,uj)|(ui,uj)∈E且σ(ui,uj)=0}，根据PMC模型的测试规则可知，N(x)中所有节点都是故障的，这与条件故障模型的条件相矛盾，所以X是正确连通分支。

引理11 假设X=｛x｝是G+中的一个平凡连通分支，那么x是故障节点。

证明假设x是正确节点，由上述引理可知，N(x)中所有节点都是故障的，这无疑和假设条件是矛盾的；如果N(x)中存在正确节点，那么X就不是平凡连通分支，这同样是矛盾的，所以X是故障连通分支，即x是故障节点。

引理10和引理11提供了2个充分条件，用以判断连通分支是否故障，本文称能被上述2个引理判断是否故障的连通分支为显性连通分支,如图2(b)所示，图中存在一个正确的显性连通分支和一个故障的显性连通分支。下面将给出条件(t,k)诊断的方法：和(t,k)诊断方法类似，本文将首先构造出G+，再由引理10和引理11识别出G+中所有显性连通分支，对故障的显性连通分支进行修复或取代，最后由正确的连通分支确定其邻居连通分支，即故障连通分支，至此一次迭代才算完成。基于上述方法，下面本文将求算出满足条件(t,k)诊断的t值和k值。

引理12 在交换超立方网EH(s,p)（1≤s≤p）中，如果故障节点集F满足条件，那么G+中一定存在显性连通分支。

证明 在此使用反证法，假设G+中不存在显性连通分支。由于，即正确节点集V-F满足条件。由显性连通分支的定义可知，V-F中任意节点至少和F中的一个节点相连，且F中不存在平凡连通分支，即如果x∈F，那么一定存在（x,y）∈E+，其中，y∈F。在此设V-F到F的边集为ERF，F到V-F的边集为EFR，显然。由上述内容可知，即这显然是矛盾。所以G+一定存在显性连通分支。

引理13假设在G+中存在显性连通分支且其都是故障的连通分支。如果，那么G+中至少存在m个显性连通分支，其中，m是一个正整数。

证明 假设G+中存在m-1个显性连通分支。由于，即。设G+中故障的且非显性的连通分支个数为S，即有运用和引理12相同原理可得，且通过运算可得（p+1）p≥（p+1）（p+2），这显然是矛盾的，所以G+中至少存在m个显性连通分支。

定理2 基于PMC模型下，交换超立方网EH(s,p)（1≤s≤p）是条件可诊断的。

由上述定理可得，交换超立方网基于PMC模型下的条件(t,k)诊断度为，而已知其在传统诊断方法下的条件诊断度为4s-3，通过运算可知，即条件(t,k)诊断度大于传统的条件诊断度。

5 结束语

本文研究了交换超立方网EH（s,p）（1≤s≤p）在PMC模型下的(t,k)诊断度和条件(t,k)诊断度。给出了一个交换超立方网EH（s,p）（1≤s≤p）是可诊断的。本文结果显示交换超立方网的(t,k)诊断度大于其传统诊断度s+1。计算交换超立方网EH（s,p）（1≤s≤p）的(t,k)诊断度的最大的困难在于选取合适的t值和k值，使Φ（t+1,k）≥t 。为了给出满足Φ（t+1,k）≥t 的t值和k值，一方面需要计算I（α），另一方面需要考虑与交换超立方网的网络结构特性的结合。此外，本文考虑了任意一个节点至少存在一个正确邻居节点条件下交换超立方网EH（s,p）（1≤s≤p）的故障诊断即条件诊断问题，得出了交换超立方网EH（s,p）（1≤s≤p）是条件可诊断的,其中，条件(t,k)诊断度

由于篇幅及时间所限，本文只考虑了在PMC诊断模型下交换立方网的(t,k)-故障诊断问题，另一个影响较为广泛的比较故障模型下的交换超立方网的故障诊断问题是下一个研究的重点。

参考文献：

[1]MALEK M.A comparison connection assignment for diagnosable of multiprocessor systems[C]//The 7th Annual Symposium on Computer Architecture.New York,United States,c1980:31-36.

[2]MAENG J,MALEKM.A comparison connection assignmentfor self-diagnosis of multiprocessor systems[C]//The 11th InternationalSymposium on Fault Tolerant Computing.Edinburgh,Scotland,c1981: 173-175.

[3]SENGUPTAA,DANBURAAT.Onself-diagnosable multiprocessorsystems:diagnosis by the comparison approach[J].IEEE Transactions on Computers.1992,41(11):1386-1396.

[4]HONG W S,HSIEH S Y.Strong diagnosability and conditional diagnosability of augmented cubes under the comparison diagnosis model[J].IEEE Transactions on Reliability,2012,61(1):140-148.

[5]KHANNNA S,PUCHS W K.A Graph partitioning approach to sequential diagnosis[J].IEEE Transactions on Computers,1997,46(1):39-47.

[6]LEE C W,HSIEH S Y.Diagnosability of two-matching composition network under the MM*model[J].IEEE Transactions on Dependable and Secure Computing.2011,8(2):246-255.

[7]HSIEH S Y,CHEN Y S.Strongly diagnosable product networks under the comparison diagnosis model[J].IEEE Transactions on Computers,2008,57(6):721-732.

[8]PREPARATAFP,METZEG,CHIENRT.Onthe connectionassignmentproblemofdiagnosablesystems[J].IEEE Transactions on Electronic Computers,1967,16(6):848-854.

[9]CHANG N W,HSIEH S Y.Conditional diagnosability of augmented cubes under the PMC model[J].IEEE Transactions on Dependable and Secure Computing,2012,9(1):46-60.

[10]ZHU Q.The conditional diagnosability of crossed cubes under the comparison model[J].International Journal of Computer Mathematics,2010,87(15):3387-3396.

[11]LIN C K,KUNG T L,TAN J J M.An algorithmic approach to conditional-faultlocaldiagnosisofregularmultiprocessor interconnected systems under the PMC model[J].IEEE Transactions onComputers,2013,62(3):439-451.

[12]LIN C K,PENG S L,TAN J J M,et al.The diagnosability of g-good-neighbor conditional-fault hypercube under PMC model[C]//2010 International Conference on Parallel and Distributed Processing Techniques and Applications(PDPTA’10).Las Vegas,USA,c2010: 494-499.

[13]CHANG G Y,CHANG G J,CHEN G H.Diagnosability of regular networks[J].IEEE Transactions on Parallel and Distributed Systems,2005,16(4):314-323.

[14]XU M,THULASIRAMAN K,XU X D.Conditional diagnosability of matching composition networks under the PMC model[J].IEEE Transactions on Circuits and Systems-II:Express Briefs,2009,56(11): 875-879.

[15]LIN C K,KUNG T L,TAN J J M.Conditional-fault diagnosability of multiprocessor systems with an efficient local diagnosis algorithm under the PMC model[J].IEEE Transactions on Computers,2011,22(10):1669-1680.

[16]ARAKI T,SHIBATA Y.(t,k)-Diagnosable system:a generalization of the PMC models[J].IEEE Transactions on Computers,2003,52(7): 971-975.

[17]CHEN C,HESIH S Y.(t,k)-diagnosis for component-composition graphs under theMM*model[J].IEEE Transactions on Computers,2011,60(12):1704-1717.

[18]CHANG G Y.(t,k)-diagnosability for regular networks[J].IEEE Transactions on Computers,2010,59(9):1153-1157.

[19]CHANGGY,CHENGH.(t,k)-Diagnosabilityof multiprocessorsystems with applications to grids and toris[J].Siam Journal on Computing,2007,37(4):1280-1298.

[20]LAI P L,TAN J J M,CHANG C P,et al.Conditional diagnosability measures for large multiprocessor systems[J].IEEE Transactions on Computers,2005,54(2):165-175.

[21]郭晨,梁家荣,葛志辉,等.基于互测PMC模型的条件诊断算法[J].电子学报,2015,43(2):255-261.GUO C,LIANG J R,GE Z H,et al.A conditional diagnosis algorithm based on ex-test PMC model[J].Chinese Journal of Electronics,2015,43(2):255-261.

[22]LOH P K K,HSU W J,PAN Y.The exchange hypercube[J].IEEE Transactions on Parallel and Distributed Systems,2005,16(9): 866-874.

[23]LIANG J R,HUANG Y,YE L C.Diagnosabilities of exchanged hypercube networks under pessimistic one-step diagnosis strategy[J].Journal of System Engineering and Electronics,2015,26(2):415-420.

[24]MA MJ,ZHUL Y.Thesuperconnectivityofexchanged hypercubes[J].Information Processing Letters,2011,111(8):360-364.

[25]LI X J,XU J M.Generalized measures of fault tolerance in exchanged hypercubes[J].InformationProcessingLetters,2013,113(14): 533-537.

Research on(t,k)-diagnosability for exchanged hypercube network

XIONG Xi,LIANG Jia-rong,MAQiang
(School of Computer and Electronic Information,Guangxi University,Nanning 530004,China)

Abstract:Fault diagnosis was an important part in the processing of network system repair.PMC was a diagnosis model which was simple and easy to be understood.Through analysis of the structure of exchanged hypercube,a generalization measure of fault diagnosis for the network system was provided,called(t,k)-fault diagnosis method.By computing,it is shown that EH（s,p）is-diagnosable and conditional-diagnosable,where1≤s≤p.The result shows that the(t,k)-diagnosability of EH(s,p)is,which is bigger than its ordinary diagnosability s+1,and the conditional(t,k)-diagnosability is,which is bigger than its ordinary conditional diagnosability 4s-3.Above results present the important theory basis for fault diagnosis of exchanged hypercube network.

Key words:exchanged hypercube network,(t,k)-diagnosability,conditional(t,k)-diagnosability,PMC model

TP393

A

10.11959/j.issn.1000-436x.2016067

2015-03-26；

2015-09-29

梁家荣，972303617@qq.com

国家自然科学基金资助项目(No.61363002)

The National Natural Science Foundation of China(No.61363002)

熊茜（1990-），男，江西丰城人，广西大学硕士生，主要研究方向为互联网络的故障诊断、并行与网络计算。

梁家荣（1966-），男，广西玉林人，博士，广西大学教授，主要研究方向为互联网络的故障诊断、并行与网络计算、算法设计与分析。

马强（1990-），男，甘肃陇南人，广西大学硕士生，主要研究方向为图论、互联网络的故障诊断。