分布式编码中广义伽马分布相关噪声模型研究

刘杰平，王琴玲，何越盛，韦岗



分布式编码中广义伽马分布相关噪声模型研究

刘杰平，王琴玲，何越盛，韦岗

（华南理工大学电子与信息学院，广东广州 510640）

针对现有相关噪声模型—Laplacian模型不能精确描述相关噪声，导致分布式视频编码(DVC, distributed video coding)系统的率失真性能不高的问题，提出像素域DVC中广义伽马分布相关噪声模型。首先分析了相关噪声的统计特性，发现Laplacian分布的峰值比实际相关噪声分布的低，然后采用广义伽马分布对相关噪声进行拟合，并给出在线估计广义伽马分布参数的方法。实验结果表明，提出的模型能较精确地描述相关噪声，且有效地改善了系统的率失真性能，并减少了解码端计算复杂度。

分布式视频编码；相关噪声模型；广义伽马分布；Laplacian分布

1 引言

传统的视频编码标准，如MPEG和H.264/AVC 等，都采用运动估计与运动补偿技术消除视频中的时间冗余，尽管它们都有较高的压缩效率，但编码器复杂度非常高。而越来越多的新型视频应用（如无线视频、移动摄像电话等）的编码设备比较简单，电源、功耗和运算资源受限，这就要求视频编码器必须具有低功耗和低运算复杂度的特点。基于Slepian-Wolf理论[1]和Wyner-Ziv理论[2]，DVC[3~8]将复杂的运动估计与运动补偿技术移到解码端，具有低编码复杂度的特点，能很好地适用于“上行(up-link)”的新型视频应用。典型的像素域DVC系统如图1所示，将输入的视频序列分为关键帧（奇数帧）和WZ帧（偶数帧），对关键帧采用传统的帧内编解码方式，在解码端关键帧独立解码后，除直接输出外，还通过帧内插值生成解码WZ帧时所需要的边信息；对WZ帧量化之后进行位平面抽取，然后由Slepian-Wolf编码器对上述位平面的比特流进行编码，得到的校验比特传输到低密度累积校验码（LDPCA, low-density parity-check accumulate）译码器。解码端为了有效地利用校验比特纠正边信息的估计偏差，需要借助原始的WZ 帧与边信息之间的残差信息，即相关噪声。在实际应用中，解码端无法获得原始的WZ帧，寻求残差所服从的概率分布的过程就是相关噪声建模。相关噪声模型与残差的概率分布越接近，且LDPCA的纠错性能越好，编码端需要传输到LDPCA译码器的校验位就越少，系统码率越低，压缩率越高，同时还可以减少LDPCA迭代译码的时间。因此，对相关噪声的准确建模是DVC系统的关键技术之一。

由于解码端不可能得到原始WZ帧，因此，利用解码端所估计的边信息与原始WZ帧之间的相关噪声离线估计相关噪声模型参数不满足实际应用。目前，许多研究文献通常利用前后向运动补偿帧差在线估计相关噪声模型参数，且认为相关噪声模型近似满足Laplacian分布[7~14]，相关的具体研究主要集中在精确的Laplacian模型参数的估计，Brites等[7]针对像素域DVC提出了帧级、块级及像素级3种粒度的参数估计算法，改善了系统整体编码效率。Deligiannis等[8,9]研究了像素域DVC的相关噪声模型与边信息相关性，指出相关噪声的分布与边信息的改变密切相关；针对分层Wyner-Ziv编码系统，提出最大似然Laplacian参数估计方法。王凤琴等[10]发现残差变换后直流系数带统计分布相比零均值Laplacian分布存在一定偏差,且系数带的相关噪声分布随时间和空间变换，提出了一种基于变换域的相关噪声分布模型自适应参数估计方法，有效提高了编码效率。房胜等[11]对影响时域相关噪声的因素进行了研究，提出了一种基于小波变换域的相关噪声模型，有效提高了DVC系统的率失真性能。Wang等[12]将相关估计嵌入到Slepian-Wolf解码器，从而保证相关估计动态地跟踪边信息的方差，提出一种自适应的相关估计方法。Fang[13]提出了一种基于滑动窗置信传播算法,在解码端同时实现信源重构和相关噪声估计。杨春玲等[14]针对子带级Laplacian 模型不能准确描述相关噪声残差子带不同区域的变化特性，以及现有算法未将相邻子带之间关系利用起来，提出了基于改进FCM 聚类的噪声模型估计方法。上述研究主要集中在精确的Laplacian分布的参数估计方面，然而，由于视频信息固有的非平稳特性和解码端不能获取当前帧信息等原因，相关噪声呈现非平稳特性。Laplacian不能反映所有的视频运动，许多学者研究了相关噪声特性，提出了新的相关噪声模型。Westerlaken等[15]根据帧间运动剧烈程度的不同，设定阈值，超过阈值的区域为冲突区域，相关噪声模型采用均匀分布，低于阈值的区域为非冲突区域，相关噪声模型采用Laplacian分布，取得了较好的效果。Maugey等[16]采用幂指数分布，本文称为广义高斯分布(GGD, generalized Gaussian distribution)，对相关噪声建模，实验结果表明，率失真性能有所提高，在某些情况下在线幂指数分布参数估计甚至比离线拉普拉斯分布参数估计效果更好。尹明等[17]研究了不同运动类型视频序列的原始帧与相应边信息之间噪声系数的分布情况，发现相关噪声信息的分布不满足某种单峰分布，提出高斯混合相关噪声模型，有效改善了率失真性能。本文研究发现，Laplacian分布与实际相关噪声分布拟合时，在相关噪声零值附近的峰值过低，且在尾部收敛比较缓慢，有较严重的拖尾现象；GGD与实际相关噪声分布拟合时，零值附近具有很高的尖峰；而广义伽马（GGA, generalized Gamma)分布拟合相关噪声时，零值附近不存在很高的尖峰，又无严重的拖尾现象，能很好地拟合实际噪声分布，显示出广义伽马分布比Laplacian分布和GGD更强的拟合相关噪声的能力。因此，本文提出像素域DVC中广义伽马分布相关噪声模型，采用广义伽马分布对像素域DVC中的相关噪声进行建模，提高了DVC系统的率失真性能，降低了解码的计算复杂度。

2 Laplacian分布与GGD相关噪声模型

在像素域DVC系统中，原始WZ帧与边信息间的残差称为相关噪声，该相关噪声分布模型常用概率密度函数描述。

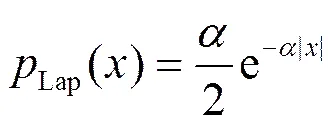
GGD的概率密度函数为

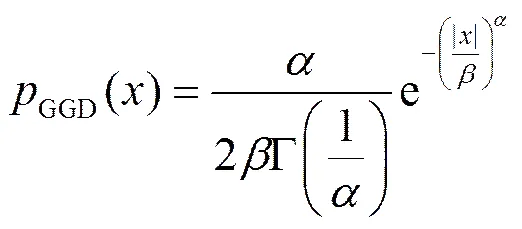
3 广义伽马分布相关噪声模型

广义伽马分布具有高度的灵活性和很强的信号拟合能力，因此受到广泛关注和研究，并应用于很多领域，但目前还没有学者将其应用于DVC系统。

3.1 广义伽马分布

广义伽马分布的概率密度函数为

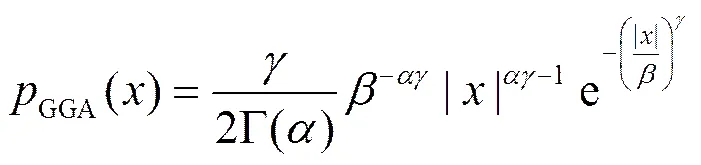
3.2 广义伽马分布相关噪声模型参数估计

从实际应用考虑，解码端无法获得原始WZ帧，在线估计相关噪声模型参数时，本文采用与文献[7, 8, 10, 17]一样的方法，利用前后运动补偿帧的残差对相关噪声建模，其中，表示像素的位置、和分别表示前后向运动补偿帧、和分别表示前后向运动矢量。假设残差服从广义伽马分布，当时，零值样本会导致式(3)数值溢出。因此，在进行广义伽马分布参数估计时，需要去除残差中所有的零值样本，对于8 bit量化的图像，残差的可能取值为[−255, 255]，则式（3）可以写成

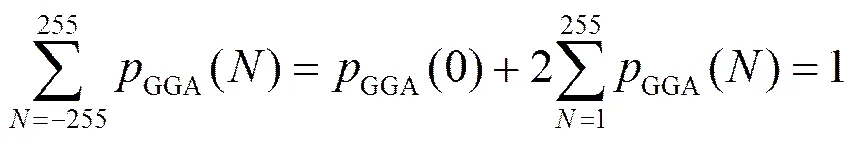
可以得到

(5)

本文广义伽马分布的参数估计方法采用最大似然估计法[18]，具体步骤如下。

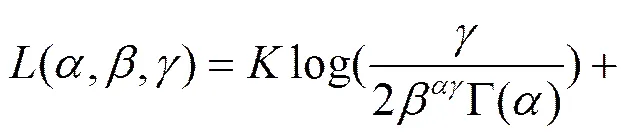
(7)

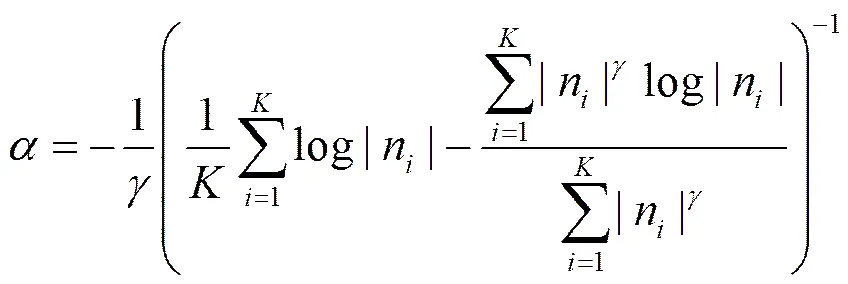
(9)

3) 解似然方程组。采用Root Isolation算法[19]求解可以得到组似然估计参数组()。

4 仿真实验

4.1 相关噪声拟合实验

为了比较Laplacian分布、GGD和广义伽马分布拟合相关噪声的性能，实验对Foreman、Soccer、Hall和Mother 4个视频序列前100帧，各随机抽取15帧（共60帧），分别进行卡方拟合检验。显著性水平分别为0.01、0.05、0.10和0.25情况下的卡方拟合检验的接受率（拟合检验结果为接受的帧的数目与拟合检验的总帧数之比）如表1所示，表中Lap、GGD和GGA分别表示Laplacian分布、GGD和广义伽马分布的卡方拟合检验结果，从表1可以看出，对于4种显著性水平， GGA分布的接受率都高于GGD和Laplacian分布。在显著性水平0.05下，卡方拟合检验的结果是：服从Laplacian分布、GGD和广义伽马分布的分别有34帧、52帧和60帧。可见，与Laplacian分布和GGD的卡方拟合检验比较，残差的分布更好地服从广义伽马分布，或者说广义伽马分布对残差的拟合能力优于Laplacian分布和GGD，这与3.1节广义伽马分布的理论特性是一致的。图2所示是上述实验中4个视频序列某帧的拟合结果。

表1 不同显著性水平下相关噪声卡方拟合检验接受率

图2中“Histogram”表示实际相关噪声的概率分布，“Lap”、“GGD”和“GGA”分别表示Laplacian分布、GGD和广义伽马分布对相关噪声的拟合。从图2可见，Laplacian分布与实际相关噪声分布比较，尾部收敛缓慢，有比较严重的拖尾现象，且峰值低于实际相关噪声分布，因此Laplacian分布与实际相关噪声分布存在较大差距；GGD与实际相关噪声分布相比，大多数部分能很好地拟合实际相关噪声分布，显示出GGD比Laplacian分布的拟合能力更强，但在零值附近GGD比实际噪声有更高的尖峰；广义伽马分布与实际相关噪声分布比较，不仅多数部分能很好地拟合实际相关噪声分布，而且，在零值附近也不存在很高的尖峰，表现出比Laplacian分布和GGD更强的拟合相关噪声的能力。

4.2 DVC系统率失真性能实验结果与分析

为了验证本文提出的广义伽马分布相关噪声模型对DVC系统率失真性能的影响，采用图1的DVC系统进行仿真实验，将其与文献[7] Laplacian分布和文献[16]GGD相关噪声模型进行比较，实验结果中分别用“GGA”、“Lap”和“GGD”表示。实验用Foreman、Hall、Soccer和Mother 4个QCIF格式，长度为101帧的视频序列；帧组长度GOP为2，奇数帧为关键帧，偶数帧为WZ帧；帧率为30 Hz；边信息的生成采用Ascenso等[20]提出的空域平滑内插算法；残差帧为前后向运动补偿帧差；实验针对视频序列的亮度分量进行，且只计算WZ帧的平均码率和平均峰值信噪比PSNR。

图3给出像素域Wyner-Ziv系统中相关噪声模型分别采用Laplacian分布、GGD和广义伽马分布时系统的率失真性能。对于每个视频序列，图3中的零码率率失真点是编码端不对WZ帧进行编码时边信息的PSNR、非零码率的率失真点与WZ帧解码的最高位平面数{1,2,3,4}相对应，即对应着解码位平面数从少到多、压缩率由大到小的情况。

从图3可见，与Laplacian分布和GGD相关噪声模型相比，在相同PSNR的情况下，对于同一视频序列，本文提出的广义伽马分布相关噪声模型不同程度降低了系统的编码码率，改善了率失真性能，且低码率比高码率时率失真性能改善更显著，从表2可见，对于Mother序列，解码平面数=1时，本文的广义伽马模型比Laplacian分布和GGD模型的码率分别降低41.55%和21.56%；解码平面数=4时，本文的模型比Laplacian分布和GGD模型的码率分别降低23.91%和17.22%。在相同码率情况下，随着码率增大，PSNR增益越大。此外，对于不同运动程度的视频序列，本文的广义伽马模型对系统率失真性能改善的程度不同，从表2可知，解码所有4个位平面，对于运动相对剧烈的Soccer序列，本文模型相对Laplacian分布和GGD模型的码率平均降低49.13%和31.41%；而对于运动相对缓慢的Mother序列，平均降低31.76%和19.46%。因此，对运动剧烈的序列，本文模型对系统率失真性能改善更显著。其原因是运动缓慢的序列，相关噪声的非平稳性较小，对噪声模型的依赖相对较小；运动相对剧烈的视频序列，相关噪声的非平稳性较大，对噪声模型的依赖也相对较大。

在模型的复杂度方面，图1中DVC系统的解码计算量主要集中在边信息生成和LDPCA迭代译码，虽然广义伽马模型参数的估计相对复杂，但采用了最大似然参数估计方法，使模型参数估计的计算量增加不大，而且，由于广义伽马模型能更精确地描述相关噪声，LDPCA译码器只需较少的校验位和迭代次数就可以成功译码，显著地节省了迭代译码的时间。与Laplacian分布和GGD模型相比，表3给出了采用本文广义伽马模型的DVC系统解码时间的节省率，从表3可见，对不同视频序列，采用广义伽马模型的系统解码时间都有不同程度的减少，与Laplacian和GGD模型相比，解码时间最少分别减少38.02%和22.24%、最多分别减少53.57%和26.85%。

表2 3种相关噪声模型在线率失真性能的比较结果

表3 采用GGA模型系统解码时间的节省率

5 结束语

为了提高DVC系统的率失真性能，针对现有Laplacian相关噪声模型不能精确地描述相关噪声问题，提出像素域DVC中广义伽马分布相关噪声模型。本文研究了不同运动程度视频序列相关噪声的统计特性，分别用Laplacian分布、GGD和广义伽马分布拟合相关噪声，发现广义伽马分布拟合相关噪声的能力相对最强；并以前后运动补偿帧差近似为实际相关噪声、采用最大似然法在线估计广义伽马模型的参数。仿真实验结果表明，提出的广义伽马相关噪声模型获得的系统率失真性能整体优于Laplacian分布和GGD模型的DVC系统，且因广义伽马分布对相关噪声模型较精确地描述，显著减少了LDPCA迭代译码的时间，从而有效减少了DVC系统解码端的计算复杂度。

[1] SLEPIAN J D, WOLF J K. Noiseless coding of correlated information sources[J]. IEEE Transactions on Information Theory, 1973, 19(4): 471-480.

[2] WYNER A, ZIV J. The rate-distortion function for source coding with side information at the decoder[J]. IEEE Transactions on Information Theory, 1976, 22(1): 1-10.

[3] AARON A, ZHANG R, GIROD B. Wyner-Ziv coding of motion video[C]//Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, IEEE, c2002: 240-244.

[4] WANG A H, ZHAO Y, BAI H H. Robust multiple description distributed video coding using optimized zero-padding[J]. Science in China Series F: Information Sciences, 2009, 52(2): 206-214.

[5] ABOU-ELAILAH A, DUFAUX F, FARAH J, et al. Fusion of global and local motion estimation using foreground objects for distributed video coding[J].IEEE Transactions on Circuits and Systems for Video Technology, 2014,25(6):973-987.

[6] SONG X D, PENG X L, XU J Z, et al. Cloud-based distributed image coding[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2015, 25(12):1.

[7] BRITES C, PEREIRA F. Correlation noise modeling for efficient pixel and transform domain Wyner-Ziv video coding[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2008, 18(9): 1177-1190.

[8] DELIGIANNIS N, MUNTEANU A, CLERCKX T, et al. Correlation channel estimation in pixel-domain distributed video coding[C]//Image Analysis for Multimedia Interactive Services. London, UK, c2009: 93-96.

[9] DELIGIANNIS N, MUNTEANU A, WANG S, et al.Maximum likelihood Laplacian correlation channel estimation in layered Wyner-Ziv coding[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 892-904.

[10] 王凤琴, 樊养余, 赵炯, 等. 基于变换域Wyner-Ziv 视频编码的相关噪声模型[J]. 数据采集与处理, 2009, 24(5): 609-614.

WANG F Q, FAN Y Y, ZHAO J, et al. Correlation noise model for transform domain WynerZiv video coding[J]. Journal of Data Acquisition & Processing，2009, 24(5): 609-614.

[11] 房胜, 李哲，梁永全, 等. 分布式视频编码虚拟依赖信道模型研究[J]. 计算机学报, 2009, 32(7):1404-1412.

FANG S, LI Z, LIANG Y Q, et al. Research of the virtual dependency channel in distributed video coding[J]. Chinese Journal of Computers, 2009, 32(7):1404-1412.

[12] WANG S, CUI L J, STANKOVI´C L, et al. Adaptive correlation estimation with particle filtering for distributed video coding[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(5): 649-658.

[13] FANG Y. Asymmetric Slepian-Wolf coding of nonstationarily- correlated-ary sources with sliding-window belief propagation[J]. IEEE Transactions on Communications, 2013, 61(12): 5114-5124.

[14] 杨春玲, 吴娟. 分布式视频编码中基于改进FCM聚类的相关噪声模型估计[J]. 中国图象图形学报, 2014, 19(2): 0185-0193.

YANG C L, WU J. Correlation noise modeling based on improved fuzzy-means clustering in distributed video coding[J]. Journal of Image and Graphics, 2014, 19(2): 0185-0193.

[15] WESTERLAKEN R P, GUNNEWIEK R K, LAGENDIJK R L. The role of the virtual channel in distributed source coding of video[C]//IEEE International Conference on Image Processing. Genoa, Italy, c2005: 581-584.

[16] MAUGEY T, GAUTHIER J, PESQUET-POPESCU B, et al. Using an exponential power model for Wyner-Ziv video coding[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. Dallax Texas. c2010: 2338-2341.

[17] 尹明, 蔡述庭, 谢云. 基于高斯混合模型的Wyner-Ziv视频编码[J]. 计算机学报, 2012, 35(1): 173-182.

YIN M, CAI S T, XIE Y. Wyner-Ziv video coding based on Gaussian mixture mode[J]. Chinese Journal of Computers, 2012, 35(1): 173-182.

[18] WINGO D R. Computing maximum-likelihood parameter estimates of the generalized Gamma distribution by numerical root isolation[J]. IEEE Transactions on Reliability, 1987, R-36(5): 586-590.

[19] JONES B, WALLER W G, FELDMAN A. Root isolation using function values[J]. BIT Numerical Mathematics, 1978, 18(3): 311-319.

[20] ASCENSO J, BRITES C, PEREIRA F. Improving frame interpolation with spatial motion smoothing for pixel domain distributed video coding[C]//5th EURASIP Conference on Speech and Image Processing, Multimedia Communications and Services. Smolenice, Slovak Republic: EURASIP, c2005: 593-598.

Research on correlation noise modeling of a generalized Gamma distribution in distributed coding

LIU Jie-ping, WANG Qin-ling, HE Yue-sheng, WEI Gang

(School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, China)

Due to the inaccuracy of modeling the correlated noise (CN)with Laplacian distribution, the rate-distortion performance of DVC is relatively low. CN modeling via generalized Gamma (GGA)distribution was proposed for pixel-domain DVC. Statistical features of the CN modeling were analyzed. It was found that Laplacian distribution peak was lower than actual CN distribution. GGA distribution was exploited to fit CN and the GGA distribution parameters were estimated online. The simulation results indicate that the proposed model can more accurately reflect the statistics features of CN, improve rate distortion performance, and reduce computation complexity.

distributed video coding, correlation noise model, generalized Gamma distribution, Laplacian distribution

TN919.8

A

10.11959/j.issn.1000-436x.2016050

2015-01-15；

2016-01-06

国家自然科学基金资助项目（No. 61327005）；国家工程技术研究中心基金资助项目（No. 2013FU125X02）

The National Natural Science Foundation of China (No. 61327005), The National Engineering Technology Research Center for Mobile Ultrasonic Detection(No. 2013FU125X02)

刘杰平（1961-），女，湖南新化人，博士，华南理工大学副教授、硕士生导师，主要研究方向为图像/视频信号处理、无线视频传输。

王琴玲（1991-），女，湖南邵阳人，华南理工大学硕士生，主要研究方向为视频编码。

何越盛（1988-），男，广西钦州人，华南理工大学硕士生，主要研究方向为视频编码。

韦岗（1963-），男，广西宾阳人，博士，华南理工大学教授、博士生导师，主要研究方向为通信、信息处理理论与技术。