中子孔隙度测井探测器气压响应数值模拟

田立立，张　锋，王新光，刘军涛

(中国石油大学(华东)地球科学与技术学院，山东 青岛　266580)



中子孔隙度测井探测器气压响应数值模拟

田立立，张锋，王新光，刘军涛

(中国石油大学(华东)地球科学与技术学院，山东 青岛266580)

摘要：在补偿中子孔隙度测井中He-3管利用(n,p)反应来探测热中子，管内灵敏区所充氦气气压对中子探测效率影响较大，决定中子孔隙度测量精度。利用蒙特卡罗方法模拟研究不同地层条件下远、近探测器计数率随He-3气压的变化规律。计算结果显示，随着He-3气压增大，近、远探测器计数先增大再趋于平缓，计数比值略有增大，孔隙度灵敏度增加，孔隙度测量误差呈幂指数减小，提高了测量精度。研究结果可为仪器研制过程中选择He-3管提供技术支持。

关键词：He-3管；灵敏区气压；中子；蒙特卡罗模拟

中子孔隙度测井是确定地层孔隙度的重要方法，其探测器一般使用BF3管和He-3管[1-2]。He-3管中子探测器是一种常用的中子探测器[3]，由于3He(n,p)3H反应截面很大，使He-3管中子探测器具有较高的探测效率，而热中子探测效率与He-3管灵敏区体积、He-3管气压、气体组合及入射中子能量等因素有关[4-8]。Ravazzani等[6]通过实验测量不同He-3气压与不同气体组合对He-3管探测特性的影响，得到一般He-3气压选择范围是4～8 atm。Lintereur等[9]利用实验和数值模拟方法研究不同He-3气压对中子探测效率的影响，验证了数值模拟方法对He-3管响应特性研究的可行性。

本文利用蒙特卡罗方法，模拟地层条件下He-3探测器的气压响应特性。建立不同孔隙度纯砂岩地层模型，改变He-3管的气压，研究241Am-Be中子源产生的中子与地层作用后的He-3管探测响应特性，为补偿中子孔隙度测井仪的结构参数优化提供技术支持。

1He-3管热中子探测原理

中子孔隙度测井主要通过源距不同的两个探测器记录来自于地层的热中子，利用计数比值确定孔隙度。进入探测器中的热中子与3He发生核反应：

带有能量的质子与氚核通过计数管中的气体时发生电离碰撞，使He-3气体分子电离，形成大量的离子对，离子对在外加电场的作用下分别向正、负电极漂移，通过多次电离碰撞，电子不断增值产生雪崩效应，形成放大信号被收集，信号与发生核反应的热中子数有关，可通过该过程来探测热中子。

2计算模型

利用蒙特卡罗方法建立的地层条件下计算模型[10]示于图1。地层为高140 cm、内外半径分别为10 cm和70 cm的圆筒状模型，由SiO2(ρ=2.65 g/cm3)和H2O组成，孔隙度分别为0，10%，20%，30%、40%和50%。井眼充满淡水，直径20 cm，井中温度为373 K。仪器紧贴井壁，241Am-Be中子源位于仪器下端，其中子能量分布[11]示于图2。近探测器源距为22.5 cm，氦气灵敏区尺寸为Φ2.5 cm×5 cm；远探测器源距为45 cm，氦气灵敏区尺寸为Φ2.5 cm×10 cm。灵敏区氦气气压从1.01×105Pa变化到2.03×106Pa，其中1.01×105～8.11×105Pa间隔5.06×104Pa，8.11×105～2.03×106Pa间隔1.01×105Pa。模拟时源中子数为5×107，利用FMn卡记录发生3He(n, p)3H反应的中子，计数误差小于2%。

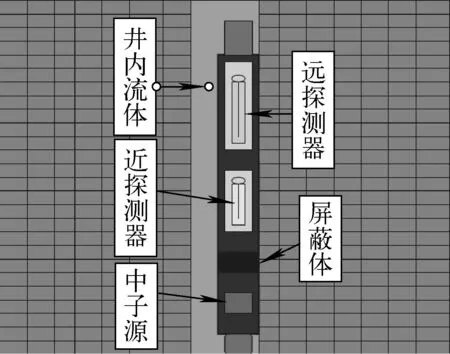
图1　计算模型Fig.1　Simulation model

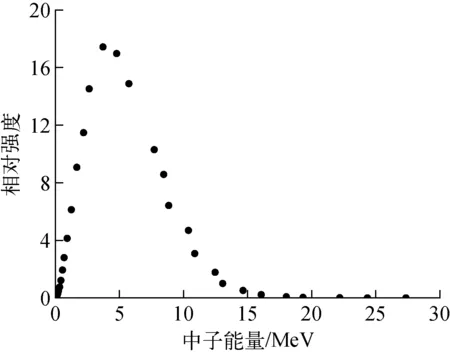
图2　中子源能量分布Fig.2　Neutron source energy distribution

3结果与讨论

3.1He-3管的响应特性

利用上述计算模型，模拟孔隙度为10%饱含水纯砂岩地层时的中子输运，近He-3中子探测器在所充氦气气压不同时的中子能量分布示于图3。由图3可知，241Am-Be中子源产生的中子进入地层，经过减速慢化后到达探测器(管内无3He)的中子能量主要分布在1 MeV以下，其强度约占总中子数的80.29%，且不同数量级能量的中子分布相当；在同样的地层条件下，He-3探测器计数随中子能量增加而急剧降低，随着探测器中He-3气压的增大，不同能量段的中子计数都有所增大。

利用以上数据可得到不同He-3气压下热中子(0～0.1 eV)的计数N1占总计数N的比值R=N1/N及中子探测效率η=N/N0，N0为管内无He-3时总中子相对计数，结果列于表1。

经过地层减速后的中子进入探测器后主要是热中子被记录，且随着气压增加，热中子计数比变化较小，但中子探测效率增加，即在灵敏体积一定条件下，管内He-3气压决定了中子的探测效率。

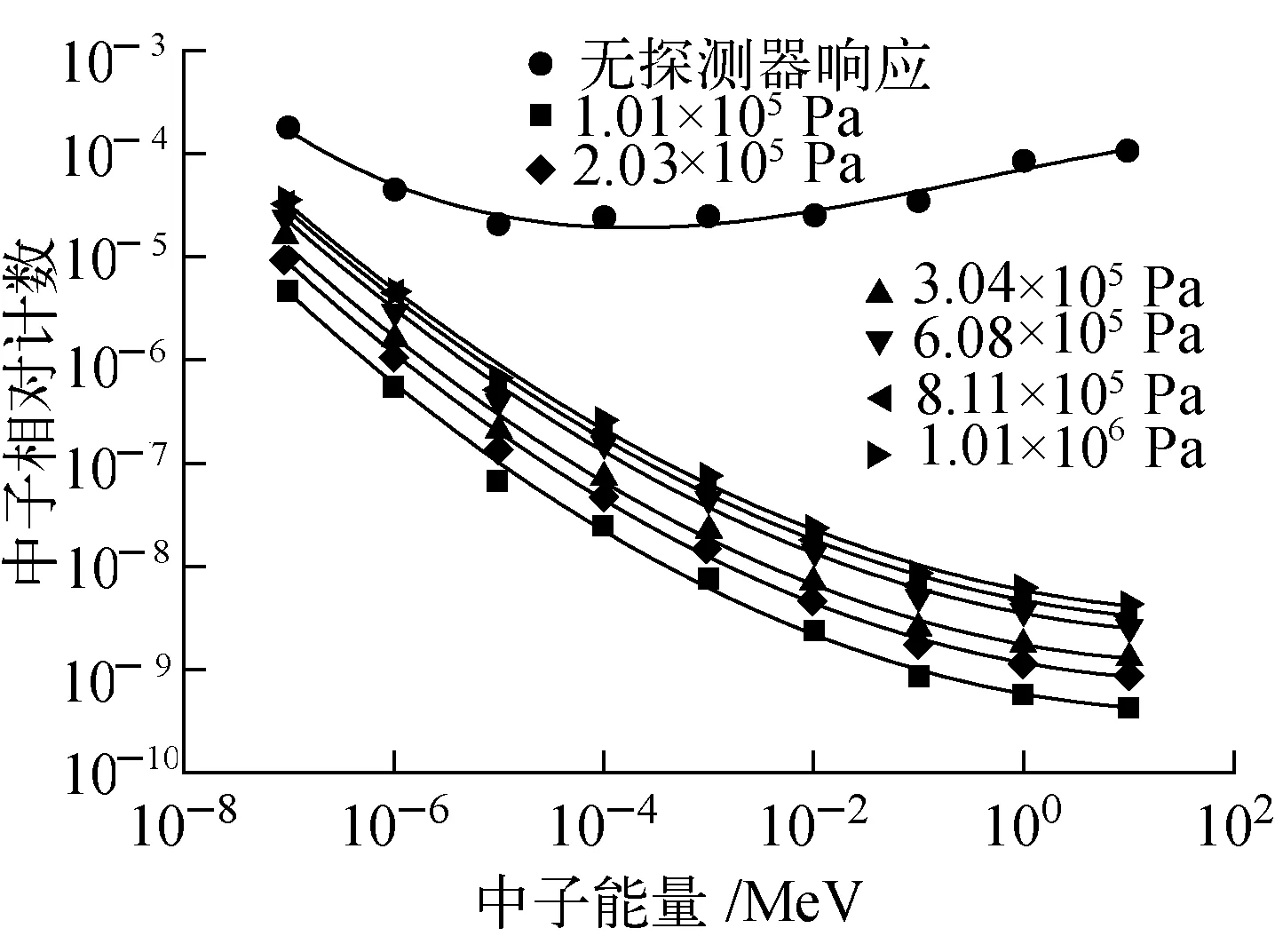
图3　不同气压情况下的中子能量分布Fig.3　Neutron energy distributionof different He-3 pressure

参数不同He-3气压下热中子分布及探测效率无He-31.01×105Pa2.03×105Pa3.04×105Pa6.08×105Pa8.11×105Pa1.01×106PaN11.8246×10-45.2803×10-61.0027×10-51.4308×10-52.5027×10-53.0792×10-53.5652×10-5N5.4699×10-45.9434×10-41.1327×10-51.6222×10-52.8655×10-53.5471×10-54.1318×10-5R33.36%88.84%88.52%88.20%87.34%86.81%86.29%η—1.09%2.07%2.97%5.24%6.48%7.55%

注：表中计数为相对一个源中子的相对计数

3.2气体压强变化对中子计数的影响

图4　远、近探测器中子计数与气压变化关系Fig.4　Relationship of neutron count of near andfar detector with different pressure

采用同样的计算模型，分别模拟孔隙为20%和40%的饱含水砂岩地层的中子输运，利用模拟得到的中子计数乘以中子产额和探测器灵敏区横截面积确定探测器中子计数，固定中子产额为4×107，远、近探测器灵敏区横截面积分别为25 cm2和12.5 cm2。分别改变远、近探测器管内的He-3气压，远、近探测器的中子计数随气体压强的变化示于图4。由图4可知，在地层条件下，中子计数随He-3气压的变化规律并不是线性的。随着He-3气压的增大，中子计数的增加程度逐渐趋于平缓。孔隙度的增大使得探测器的计数有所降低，可见高孔隙度地层中的水对中子有较强的减速效果。

3.3不同气压条件下中子孔隙度响应特性

3.3.1不同气压条件下孔隙度响应

利用图1的计算模型，设置地层孔隙为10%、20%、30%、40%和50%的饱含水砂岩，分别在不同孔隙度地层模型下设置He-3气压为4、6、8、10 atm，保持其他结构参数不变。记录不同孔隙度模型下近、远探测器的中子计数率随气体压强的变化，并计算二者的比值Ns/NL，同一坐标系下Ns/NL随孔隙度的变化规律示于图5。由图5可以看出，随着气体压强的增大，近、远探测器的中子计数之比有所增加，且随着孔隙度的增大，增加的程度也略有增大。

3.3.2不同气压条件下孔隙度灵敏度对比

利用图5数据拟合气压为4.05×105、6.08×105、8.11×105、1.01×106Pa时近、远探测器计数之比与孔隙度的响应关系式分别为：

R=3.736+0.127 6φ-0.000 834 6φ2

(1)

R=3.804+0.130 5φ-0.000 846 2φ2

(2)

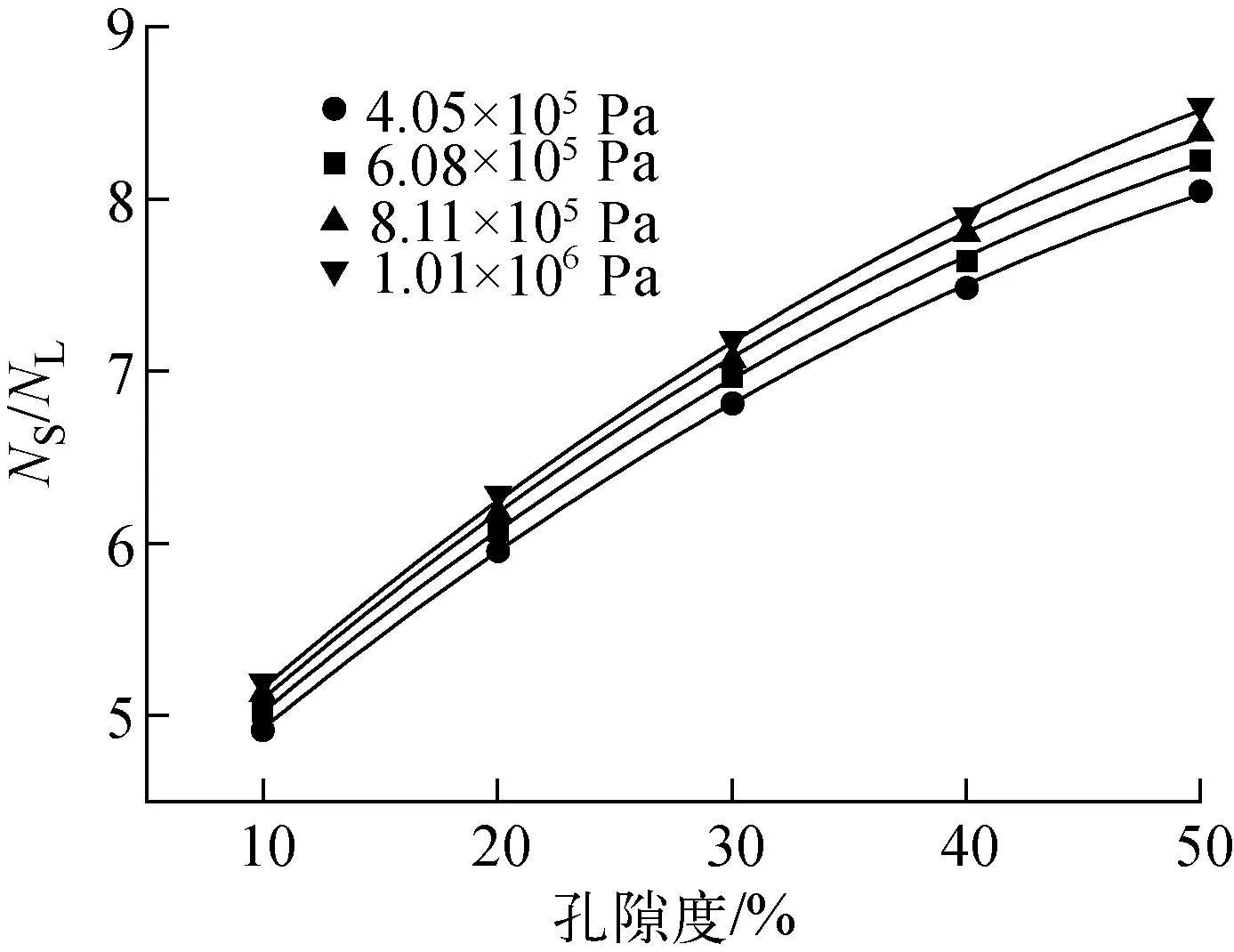
图5　Ns/NL随孔隙度的变化Fig.5　Relationship of Ns/NLand porosity

R=3.846+0.134 2φ-0.000 878 7φ2

(3)

R=3.912+0.133 3φ-0.000 824 3φ2

(4)

表2　不同气压的孔隙度灵敏度对比

3.3.3He-3管气压对孔隙度测量误差的影响

利用以上数据，拟合孔隙度与近、远探测器计数比值的关系，根据误差传递原理计算孔隙度测量误差。测井速度500 m/h，中子源产额每秒4.0×107个时，不同气压及孔隙度条件下的中子孔隙度测量误差示于图6。由图6可以看出，随着气压的增大，孔隙度测量误差呈规律下降。在当前模拟条件下，当要求在最高孔隙度为20%左右的地层中测量中子孔隙度，且孔隙度测量误差小于1%时，则需要He-3气压不小于10 kPa。在实际应用中可根据地层条件适当提高He-3管气压，提高中子孔隙度测量精度。

考虑到探测器计数饱和问题，保持近探测器的He-3气压为4.05×105Pa，改变远探测器的He-3气压分别为6.08×105、8.11×105、1.01×106Pa，计算三种探测器组合对中子孔隙度测量误差的影响，结果示于表3。由表3可知，保持近探测器He-3气压不变，远探测器He-3气压的增大同样可以提高孔隙度测量精度。

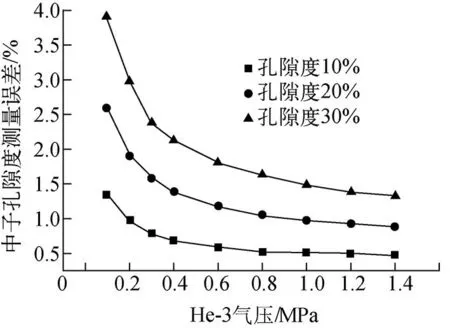
图6　中子孔隙度测量误差随气压的变化Fig.6　Relationship of neutron porositymeasurement error with different pressure

孔隙度φ近、远探测器气压相同组合近、远探测器气压不同组合4.05×105Pa6.08×105Pa8.11×105Pa1.01×106Pa6.08×105Pa8.11×105Pa1.01×106Pa10%0.68%0.58%0.52%0.51%0.61%0.57%0.56%20%1.39%1.18%1.06%0.98%1.23%1.14%1.07%30%2.12%1.80%1.63%1.48%1.86%1.72%1.61%

4小结

(1) He-3探测器气压的增大使中子计数增加，且增加的程度随着气压升高而趋于平缓。

(2) 随着He-3气压的增大，近、远探测器的中子计数之比增加，同时气压增大时孔隙度灵敏度略有增加，相对孔隙度灵敏度基本保持不变。

(3) 随着He-3气压的增大，中子孔隙度测量误差呈幂规律下降，在实际应用中可根据地层条件适当提高He-3管气压，从而有效地提高中子孔隙度测量精度。考虑到计数饱和，只提高远探测器He-3气压，以提高测量精度。

参考文献：

[1]黄隆基.核测井原理[M]. 东营：石油大学出版社，2000：249-259.

[2]付广智,何彬,章喜喜,等. BF3中子探测器阵列探测效率的蒙特卡罗计算[J]. 核电子学与探测技术,2006,26(1):65-67.

Fu Guangzhi, He Bin, Zhang Xixi, et al. Detector efficiency computed with Monte Carlo method of the BF3neutron detector array[J]. Nuclear Electronics& Detection Technology, 2006, 26(1): 65-67(in Chinese).

[3]张明,施俊,任忠国.3He中子计数管的机理及结构[J]. 核电子学与探测技术,2009,29(5):1 170-1 171.

Zhang Ming, Shi Jun, Ren Zhongguo. The theory and configuration of3He neutron counting tube[J] . Nuclear Electronics& Detection Technology, 2009, 29(5): 1 170-1 171(in Chinese).

[4]杨巧荣. 4π球形3He中子探测器的蒙特卡罗模拟研究及设计[D]. 兰州：兰州大学,2011.

[5]刘应都,张国强,王宏伟,等.3He 正比计数器探测效率模拟及灵敏度刻度[J]. 核技术，2012,35(3):175-178.

Liu Yingdu, Zhang Guoqiang, Wang Hongwei, et al. Simulation of detection efficiency for a3He proportional counter and its sensitivity calibration[J]. Nuclear Techniques, 2012, 35(3): 175-178(in Chinese).

[6]Ravazzani A, Foglio P A, Jaime R, et al. Characterization of3He proportional counters[J]. Radiation measurements, 2006, 41(5): 582-593.

[7]Bystritsky V M, Slepnev V M, Boreiko V F, et al.3He detectors in experiments at the powerful pulsed accelerators[J]. Nuclear Instruments and Methods in Physics Research, 2002, 490(1-2): 344-355.

[8]夏凌志,张建民,杨志高,等. 蒙特卡罗方法在补偿中子测并仪器设计中的应用[J]. 测井技术,2003,27(6):77-480.

Xia Lingzhi, Zhang Jianming, Yang Zhigao, et al. Application of Monte Carlo Method in compensated neutron log tool design[J]. WLT, 2003, 27(6): 477-480(in Chinese).

[9]Lintereur A, Conlin K, Ely J, et al.3He and BF3neutron detector pressure effect and model comparison[J]. Nuclear Instruments & Methods in Physics Research, 2011, 652(1): 347-350.

[10]张锋,靳秀云,侯爽. D-T 脉冲中子发生器随钻中子孔隙度测井的蒙特卡罗模拟[J]. 同位素,2010,23(1):15-21.

Zhang Feng, Jin Xiuyun, Hou Shuang. Monte Carlo simulation on compensated neutron porosity logging in LWD with D-T pulsed neutron generator[J]. Journal of Isotopes, 2010, 23(1): 15-21(in Chinese).

[11]Fantidis J, Nicolaou G, Potolias C, et al. The comparison of four neutron sources for Prompt Gamma Neutron Activation Analysis (PGNAA) in vivo detections of boron[J]. Journal of Radio analytical and Nuclear Chemistry, 2011, 290 (2): 289-295.

Monte Carlo Study on Gas Pressure Response of He-3 Tube in Neutron Porosity Logging

TIAN Li-li, ZHANG Feng, WANG Xin-guang, LIU Jun-tao

(SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

Abstract:Thermal neutrons are detected by (n,p) reaction of Helium-3 tube in the compensated neutron logging. The helium gas pressure in the counting area influences neutron detection efficiency greatly, and then it is an important parameter for neutron porosity measurement accuracy. The variation law of counting rates of a near detector and a far one with helium gas pressure under different formation condition was simulated by Monte Carlo method. The results showed that with the increasing of helium pressure the counting rate of these detectors increased firstly and then leveled off. In addition, the neutron counting rate ratio and porosity sensitivity increased slightly, the porosity measurement error decreased exponentially, which improved the measurement accuracy. These research results can provide technical support for selecting the type of Helium-3 detector in developing neutron porosity logging.

Key words：Helium-3 tube; counting area gas pressure; neutron; Monte Carlo simulation

收稿日期：2015-04-20;修回日期：2016-01-05

基金项目：国家自然科学基金(41374125，41574119)；中央高校基本科研业务费专项资金资助(14CX05011A)

作者简介：田立立(1993—)，男，陕西咸阳人，硕士研究生，从事核测井方法基础研究 通信作者：张锋，教授，E-mail: zhfxy_cn@upc.edu.cn

中图分类号：TL816+.3

文献标志码：A

文章编号：1000-7512(2016)02-0098-05

doi：10.7538/tws.2016.29.02.0098