一个简洁的圣维南方程组推导过程

（郑州大学水利与环境学院，河南郑州450001）

（郑州大学水利与环境学院，河南郑州450001）

圣维南方程组是明渠非恒定渐变流基本微分方程组。它是由连续性微分方程式和运动（能量）微分方程式所构成。由于渐变流又是非恒定流，运动要素既随流程变化也随时间变化，推导连续性微分方程式时只考虑一阶微量项，直接忽略二阶微量项。明渠流是水位变化产生的重力流。运动（能量）微分方程式推导时，把水位看成是由底部高程和水深所构成，两者独立分析，分别得出重力和压力对流动的影响。这样的推导过程简洁明了且概念清楚，易于教学。

水力学；明渠流；非恒定流；圣维南方程组

引言

圣维南方程组是明渠非恒定渐变流基本微分方程组。它是由连续性微分方程式和运动（能量）微分方程式所构成。［1］由于是非恒定流，运动要素随时间变化。由于是非均匀渐变流，运动要素又随流程坐标变化。选取微元体作为研究对象，并考虑运动要素在微小时段内变化时，就涉及到空间和时间两个微小变量。如不能区分微量的量级，使推导过程统一在一个必要的尺度上，忽略相对的高阶微量项，将十分繁琐，主次不明。由于是渐变流，流线不相互平行。水面线和底坡线作为两条特殊的流线也是不相互平行的。在推求运动（能量）微分方程式时，压力、重力、阻力及加速度等矢量，均应是在所分析方向上的投影。明确投影方向，并将产生压力差和重力分量的因素清晰的隔离开来，将会使推导过程简洁明了、概念清晰、方便理解。

一、连续性微分方程式的推导

连续性微分方程式由质量守恒定律推导，是质量守恒定律在明渠非恒定流流动中的体现。

如图1所示，运用欧拉法，选取上游u-u断面和下游d-d断面之间控制体内的液体作为研究对象。流段长度为ds。

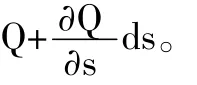
图1连续性微分方程式推导

那么，dt时段内由u-u断面流入的液体质量为：ρQdt

那么，t时刻控制体内液体质量为：ρAds

由质量守恒定律，dt时段内由于交换而引起控制体内液体的质量增量与由于非恒定而引起控制体内液体的质量增量相等：

此式即为圣维南方程组中连续性微分方程式的形式。与经典形式完全相同。［1］

二、运动（能量）微分方程式的推导

运动（能量）微分方程式由牛顿第二定律推导，反映的是明渠非恒定渐变流流动中力与运动要素之间的关系，也是反映功能转换的关系。

图2运动（能量）微分方程式推导

如图2所示，选取流程坐标s至s+ds流段的水流作为研究对象。

由于每个过水断面水位均是由渠底高程和水深所构成，即z=z0z+h。则为了简单起见，把水位变化分割开来，分别单独考虑渠底高程和水深变化对水流的影响。

图3压力分量推导示意图

当只考虑底坡变化而不考虑水深变化时，即相当于均匀流的情况。如图4所示。则重力在流动方向的分量为：ρgAdsi。

图4重力分量推导示意图

不难得出该流段水流所受到阻力分量的表达式为：Ff=-τ0χds

控制体内液体所受到合外力在流动方向上的分量为：

此式即为圣维南方程组中运动（能量）微分方程式的形式。与经典形式完全相同。［1］

三、结束语

圣维南方程组中连续性微分方程式推导过程中，分析由于流量沿程变化而引起控制体内质量变化时，可忽略水力要素随时间的变化，均用初始时刻的值进行计算；分析控制体内液体体积随时间变化而引起质量变化时，可忽略由于断面位置不同而引起水力要素的变化，均以上游断面水力要素来进行计算。运动（能量）微分方程式推导过程中，把水位分割成渠底高程和水深两部分，仅考虑渠底高程变化时计算重力的作用，仅考虑水深变化时计算压力的作用。这样的推导过程简洁明了、概念清楚，易于教学。

［1］吴持恭.水力学与山区河流开发保护国家重点实验室（四川大学）.水力学（第4版）（下册）［M］.北京：高等教育出版社，2008：76-80.

一个简洁的圣维南方程组推导过程

李占松 师冰雪

The Saint-Venant equations are the basic differential equations of unsteady gradual flows in open channels.It consists of the continuous differential equation and motion（energy）differential equation.Because the gradually varied flow is unsteady and the movement elements changed with the changing of flow path and time，we can only consider the first order trace and neglect the second order trace when the continuous differential equation is derived.The open channel flow is a gravity flow resulted from the change of water level.When the motion（energy）differential equation derived，the water level is taken as consisting of the bottom elevation and the depth of the water，then the two parts are analyzed independently，differentiate the effect of gravity and pressure on the flow.This derivation is concise and clear and also easy for teaching.

hydraulics；open channel flow；unsteady flow；the Saint-Venant equations

G642文献标志码：A文章编号：2096-000X（2016）18-0097-02

李占松（1965-），男，汉族，河南长葛人，副教授，博士，主要从事计算水力学及工程水力学方面的研究。