城市道路路段行程时间计算模型研究

李　昂， 李　硕， 李　玲

(湖南大学 土木工程学院， 湖南 长沙　410082)



城市道路路段行程时间计算模型研究

李昂， 李硕， 李玲

(湖南大学 土木工程学院， 湖南 长沙410082)

[摘要]针对城市道路路段车辆行程时间的计算和预测问题，以城市道路网络中典型的道路路段和信号控制道路交叉口为研究对象，采用道路交通信息视频采集技术获得基本的道路交通信息数据。通过对道路路段及其下游信号控制道路交叉口交通流特性分析，重新建立和标定了城市道路路段车辆行程时间计算模型和下游信号道路交叉口交通延误计算模型，其二者之和正是由道路路段及其下游信控交叉口构造而成的典型的城市道路车辆行程时间。通过实例计算与对比分析，结果表明，该模型具有较好的适用性和准确性。

[关键词]行程时间； 城市道路； 计算模型

1概述

近年来，世界上许多国家都很重视ITS系统的研究与开发，在城市道路车辆行程时间计算预测方面也取得了一些成果，如IwaoOkotani[1]利用卡尔曼滤波理论建立了城市道路路段车辆行程时间的预测模型，其预测结果优于在此之前常用的历史平均预测模型的结果；Dougherty和Clark[2]分别将人工神经网络运用于短时道路交通流预测，一定程度上消除了建立精确数学模型的困难。

在我国，许多专家学者也都在从事城市道路路段车辆行程时间问题的研究，主要集中在通过道路交通流基本理论进行模型公式的推导[3]和利用时间序列、智能神经网络等[4，5]来建立道路路段行程时间的计算模型。但普遍存在高峰期城市道路交通流密度较大时的精度不高的问题，主要原因在于建模时对道路路段下游道路交叉口交通延误情况考虑不足，车辆在道路路段下游交叉口处产生的交通延误随着道路交通流密度的变化而有敏感的差异，而现有模型往往把整个道路路段视为相同的情况来考虑，致使模型在道路交通流密度较小时有较好的精度，在当道路交通流密度变大时，计算结果与实际情况相差很大。

因此，在计算城市道路路段车辆行程时间时，本文根据道路交通流在城市道路路段上的两种不同的状态，将车辆在城市道路路段的行程时间T分为两部分：即车辆在城市道路路段上游的行程时间Tup和在道路路段下游交叉口处的交通延误d，如图1所示。

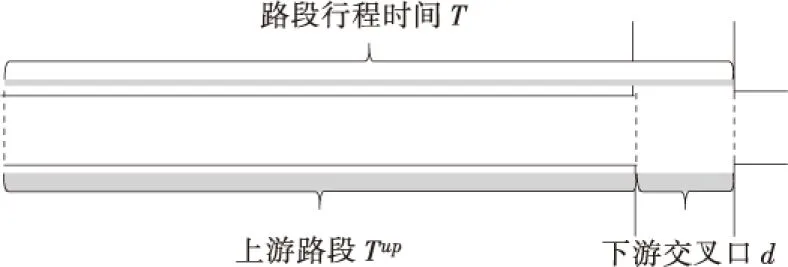
图1　城市道路路段的构造及其车辆行程时间划分Figure 1　The division of vehicle travel time on urban road segment as well as at its downstream intersection

2上游道路路段行程时间计算模型

2.1模型建立

车辆在城市道路路段上的行程时间主要取决于道路技术条件和道路交通流状况。本文从最基本的道路交通流的速度-流量模型入手建立计算模型。

在道路交通流的速度-流量函数模型的研究中，美国联邦公路管理局(BPR)的模型即BPR道路阻抗函数是最具代表性的一个研究成果，影响巨大，使用也很广，在美国道路通行能力手册2010版(HCM2010)中其表达式为：

(1)

式中：v为城市道路路段的实时行程车速，km/h；v0为城市道路路段的自由流行程车速，km/h；q为城市道路路段的交通流量，pcu/h；c为城市道路路段的实际通行能力，pcu/h；α、β为模型参数，α的推荐取值0.15，β的推荐取值4.0。

BPR模型是美国联邦公路局对大量低饱和度流量的公路进行交通调查后，通过回归分析得到的，但仅考虑非饱和状态下道路机动车流量。模型在描述高饱和状态或超饱和状态下的道路交通流时，计算结果与实际道路交通状况误差较大。

以最常用的α=0.15，β=4.0为例，随着道路交通饱和度的增加，BPR模型与实际情况的吻合度越来越低，当交通饱和度较低(如q/c<0.5)时，道路交通量的增加对交通阻抗的影响很小，几乎可以忽略不计；当道路交通饱和度达到1时，行程车速下降量仅为20%，当道路交通量继续增大(q/c>1.0)时，行程车速也只是缓慢下降。而根据相关研究中实际道路交通调查数据显示[6]，当道路交通量接近道路通行能力，即交通饱和度接近1时，实际行程车速只有自由流车速的一半，甚至更低。说明采用固定α、β推荐值的BPR模型在高交通饱和度时计算结果误差较大。因此，在国内城市道路交通条件下，必须对模型进行改进，对交通阻抗模型中的参数进行重新标定。

本文根据国内城市道路交通的实际状况以及BPR模型存在的不足，提出基于BPR阻抗模型的修正模型：

(2)

β=b1+b2(q/c)

(3)

式中：α、β、b1、b2为模型参数；其他变量如前所定义。

与BPR模型相比，修正模型确定了参数β的线性计算公式，不再单一取固定参考数值，这是由于在用实测数据进行回归分析时发现，当β取固定值时，得到的模型曲线与实测数据拟合较差，而当β是关于q/c的线性组合时，模型曲线与实测数据有较好的拟合度。参数α则用来控制当道路交通流量q与道路通行能力c相等时，等于实测行程车速v与自由流行程车速v0的比值，使得模型曲线在交通饱和度等于1时能够连续，这样也同时可以减少对道路通行能力c的约束。

2.2模型参数标定

为了精确的标定上述模型参数，获取准确的道路交通调查数据，于2014年9月22日至9月28日，每天下午4：30-6：30时段进行了连续6d的城市道路交通调查。调查选择在比较有代表性的长沙市主干路潇湘中路进行，调查地点为潇湘中路新民路口-桃子湖路口、桃子湖路口-牌楼路口、牌楼路口-天马路口3个双向道路路段及其交叉口。调查方法选用视频牌照法，通过在道路路段上下游停车线处架设摄像机连续拍摄，得到在该道路路段上通行的车流视频资料，如经过上下游拍摄点的时刻、车牌、车型、颜色等，如图2和图3所示，通过数据处理，进而获得了相应时间的3个道路路段的车辆实际行程时间、交通延误、交通量、车辆速度等数据。

运用本文3个道路路段由北向南的交通调查数据，采用实测数据回归分析的方法，对参数α、β、b1、b2标定。

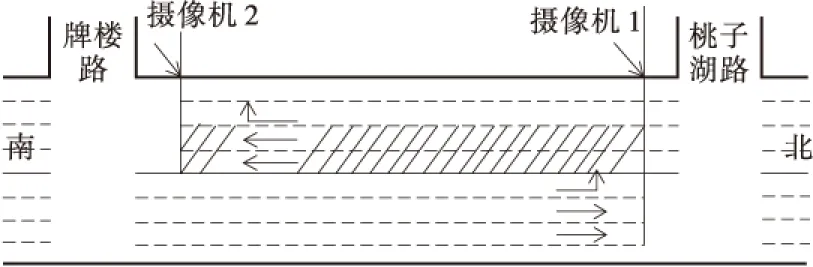
图2　桃子湖路-牌楼路路段(由北往南)交通调查Figure 2　Taozi lake road-pailou road sections(south bound)traffic survey

图3　同一车辆经过两个不同拍摄点的视频图像

Figure3Thevideoimagesofthesamevehiclepassingtwodifferentlocations

首先标定α值，由公式(2)可知：当道路路段交通流量q达到道路路段通行能力c，即q/c等于1时，道路路段行程车速v只与道路路段自由流行程速度v0有关，即：

(4)

选取道路交通调查数据中，当道路路段交通流量等于道路路段通行能力时车辆的行程速度值，并结合道路路段自由流行程速度v0，就能很容易得到α的值，求平均值即为最终标定的α值。

其次，由已经分析出的β的线性组合形式，确定b1、b2的值。在α值已知的前提下，由道路交通调查数据中道路路段交通流量q及道路路段自由流行程速度v0，很容易得到相应的β值，通过一元函数线性回归，就得到了b1、b2的标定值，如图4所示。

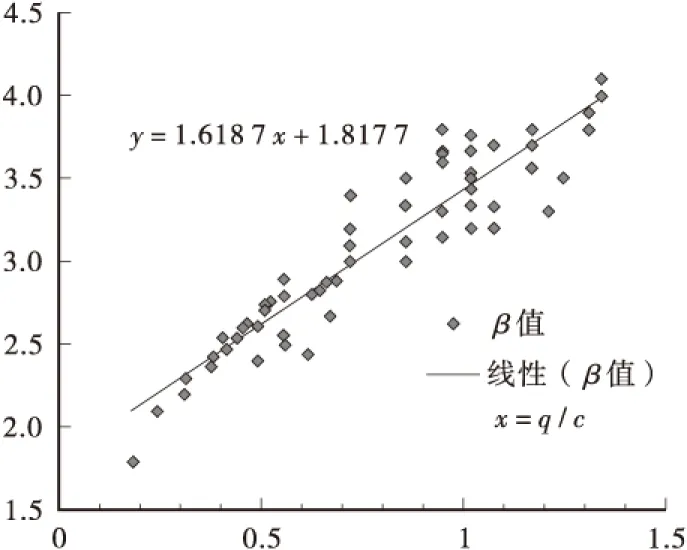
图4　关于β值的线性拟合曲线Figure 4　The linear fitting curve of vale β

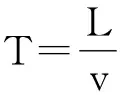
(5)

式中：Tup为上游道路路段车辆平均行程时间，s；L为上游道路路段长度，km；q为上游道路路段交通量，pcu/h。道路路段行程时间计算模型与BPR模型计算结果对比，见图5。

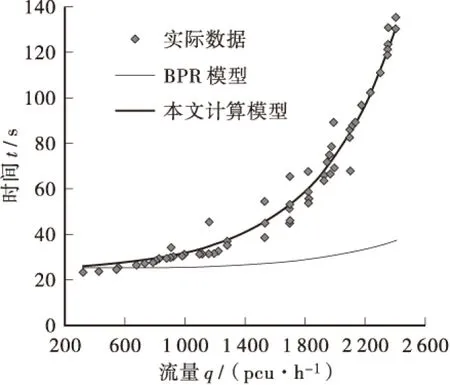
图5　道路路段行程时间计算模型与BPR模型计算结果对比Figure 5　The comparison between the results of the link travel time model proposed by the authors and the BPR model

3下游信号道路交叉口交通延误计算模型

当前信控道路交叉口交通延误的计算方法，可以分为3类：第一类，直接进行道路交通调查，其中点样本法运用的最为广泛；第二类，通过对现状道路交通流做出假设，运用数学方法进行建模，求得信控道路交叉口的交通延误时间。其中应用最为广泛的就是美国道路通行能力手册HCM2010模型；第三类，利用交通仿真类软件，对道路网中的交通量进行模拟仿真，利用软件的内部系统来计算信控道路交叉口的交通延误。

本文将以HCM2010模型为基础进行建模计算，采用实际道路交通调查数据验证本文所建模型计算结果的准确性。

3.1HCM2010交通延误计算模型

美国交通研究委员会于2010年出版了最新一版的道路通行能力手册即HCM2010，该模型如下所示，由以下3部分组成：

d=d1+d2+d3

(6)

式中：d为平均控制延误，s/veh；d1为标准交通延误，s/veh；d2为增量交通延误，s/veh；d3为初始车辆排队延误，s/veh；一般地，若分析开始时刻无车辆排队，则d3=0。

其中：

(7)

(8)

式中：C为调查的信控道路交叉口的信号周期时间，s；g为调查的信控道路交叉口的某一相位有效绿灯信号时间，s；X为调查的信控道路交叉口的饱和度；T为调查的信控道路交叉口的分析时段长度，h；一般取15min，即T=0.25h；c为调查的信控道路交叉口的某一进口道通行能力，pcu/h；K为调查信号道路交叉口所增加的交通延误影响因素，若是固定配时的信号交叉口时，K=0.5；I为调查的信控道路交叉口的上游影响调整因素。对单个信控道路交叉口来说，I=1.0。

从模型中可以看出：一般的研究开始无初始车辆排队，信控道路交叉口交通延误计算模型主要由两部分组成，其中第一部分为标准交通延误d1，第二部分则为过饱和交通流产生的增量延误d2。

为了了解信控道路交叉口交通延误的两个组成部分各自所占得比重，以及模型产生计算误差的来源，首先利用模型进行实例计算，将计算的结果与实际调查的交通延误数据进行对比分析。

利用HCM2010模型公式(6)～公式(8)分别计算总交通延误d、标准交通延误d1、以及增量延误d2，其计算结果如表1所示。

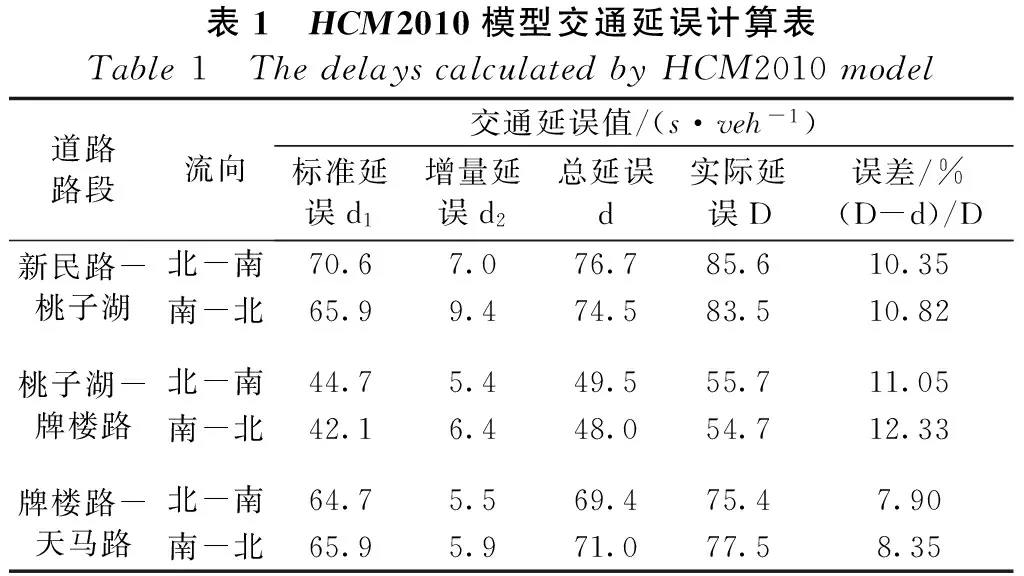
表1 HCM2010模型交通延误计算表Table1 ThedelayscalculatedbyHCM2010model道路路段流向交通延误值/(s·veh-1)标准延误d1增量延误d2总延误d实际延误D误差/%(D-d)/D新民路-桃子湖北-南70.67.076.785.610.35南-北65.99.474.583.510.82桃子湖-牌楼路北-南44.75.449.555.711.05南-北42.16.448.054.712.33牌楼路-天马路北-南64.75.569.475.47.90南-北65.95.971.077.58.35

由上表结果可以看出：各个道路路段采用HCM2010模型计算的交通延误与实测的交通延误有一定的误差，最高达到了12.33%，且HCM2010模型计算值均比实测值要小。

这主要因为HCM2010交通延误计算模型是针对美国城市信控道路交叉口的交通流特性建立的，其模型参数的选取都是根据其城市道路交通流特征来确定，而我国城市信控道路交叉口与美国的有很大的差异。主要表现在：首先，道路交通组成不同。我国城市道路交通组成比较复杂，机非混合交通比较多，不同种类交通之间相互干扰多；其次，车辆驾驶员的驾驶习惯及驾驶水平不同。我国城市道路上的交通流往往会有因为车辆驾驶员原因引起的各种干扰，造成了城市信控道路交叉口交通延误的增加。

由此可以看出，虽然HCM2010交通延误计算模型经过了美国大量的调查数据的回归分析和验证，但是针对我国城市信控道路交叉口计算的结果仍与实际存在着一定的误差。因此，本文中参照HCM2010交通延误计算模型作为分析我国城市信控道路交叉口交通延误计算的基本模型，然后做出适应我国城市道路交通特征的模型修正，并在此基础上对模型进行重新标定。

3.2模型参数标定

以HCM2010中的城市信控道路交叉口交通延误模型为基础，其计算模型的基本形式如下所示：

(9)

式中：d为城市信控道路交叉口车均总交通延误，s/veh；A为待定系数；其他变量如前所定义。

又从上节的表(1)可以看出：在组成HCM2010城市信控道路交叉口交通延误模型的两部分中，标准交通延误部分d1的值比增量延误d2大的多，平均约占其总交通延误的90%，是城市信控道路交叉口交通延误的主要部分，所以本文将重点改进这一部分的模型，其中标准交通延误d1计算公式为：

(10)

式中：d1为城市信控道路交叉口车均标准交通延误，s/veh；A为待定系数，美国HCM2010中取A=0.5；其他变量如前所定义。

从标准交通延误模型的基本形式可以看出：模型中的待定系数A值是与模型正相关的，也就是说，随着A值的逐渐增大，模型的计算结果也应逐渐增大。又从上节可知：以美国HCM2010城市信控道路交叉口交通延误模型(其中A值取0.5)来计算，其结果总是比实际值偏小，因此随着A值的增大，模型的计算结果逐渐增大，与实际值的误差也逐渐减小。

因此本文考虑重新标定A的值来改进上述模型，从其原始赋值0.5的正向进行选择标定，这里取间隔为0.03，采取不同的A值进行城市信控道路交叉口交通延误的计算，其计算结果如表2所示。

通过计算各A值下的城市信控道路交叉口交通延误值与实际交通延误值的平均相对误差值(MRE)、平均绝对误差(MAE)、和均方根误差值(RMSE)来判定最合适的A值，其误差计算结果如表3所示。

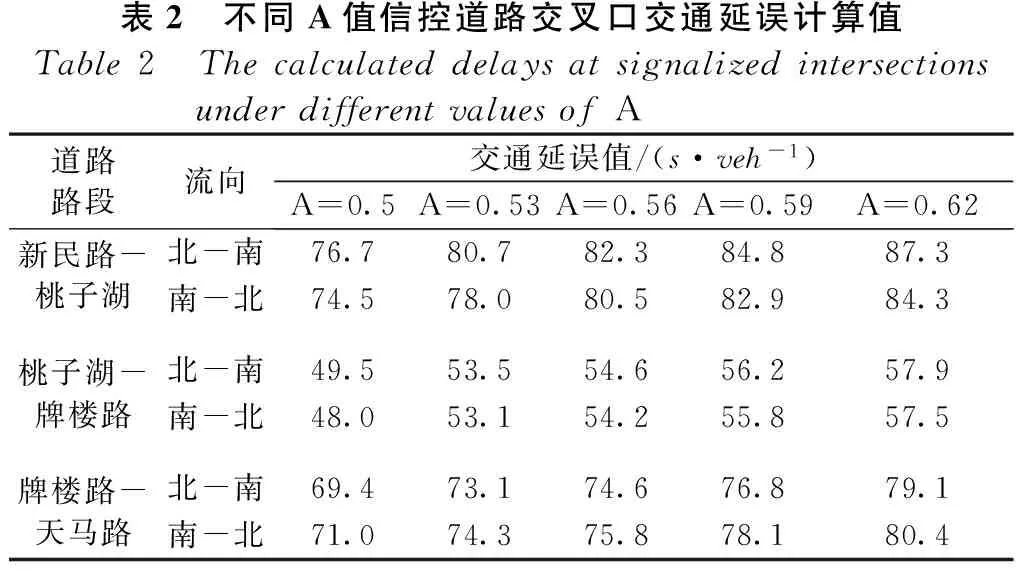
表2 不同A值信控道路交叉口交通延误计算值Table2 ThecalculateddelaysatsignalizedintersectionsunderdifferentvaluesofA道路路段流向交通延误值/(s·veh-1)A=0.5A=0.53A=0.56A=0.59A=0.62新民路-桃子湖北-南76.780.782.384.887.3南-北74.578.080.582.984.3桃子湖-牌楼路北-南49.553.554.656.257.9南-北48.053.154.255.857.5牌楼路-天马路北-南69.473.174.676.879.1南-北71.074.375.878.180.4

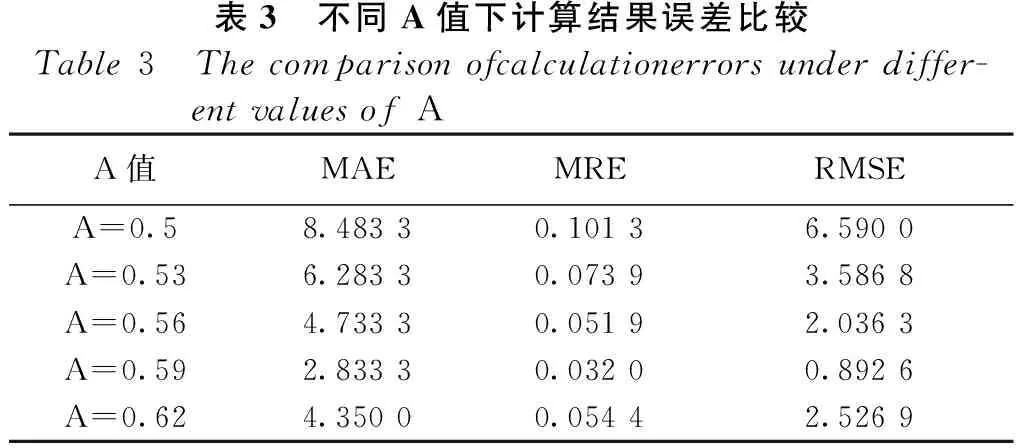
表3 不同A值下计算结果误差比较Table3 Thecomparisonofcalculationerrorsunderdiffer-entvaluesofAA值MAEMRERMSEA=0.58.48330.10136.5900A=0.536.28330.07393.5868A=0.564.73330.05192.0363A=0.592.83330.03200.8926A=0.624.35000.05442.5269

由表3可知：在A取0.59时，各误差均误差最小。因此，根据本文调查数据，模型中参数A的标定值为0.59。

本文选取的城市道路路段单一车道的通行能力为1 800pcu/(h·l)，T为分析时段长度h，一般取0.25h；对于固定信号配时控制的道路交叉口，K=0.5；信控道路交叉口的影响因素为I=1.0，如此，得到了符合所调查区域的道路交通流特征的信号道路交叉口交通延误的计算模型：

(11)

式中：d为城市信控道路交叉口车均总交通延误，s/veh；其他变量如前所定义。

4道路路段总行程时间计算模型

本文根据交通流在道路路段上的2种不同的状态，将城市道路路段车辆行程时间T分为两部分：即在道路路段上游的车辆行程时间TUP和在下游道路交叉口处的车均交通延误时间d。

T=TUP+d

(12)

因此，联立之前推导出的城市道路路段上游的行程时间模型计算公式(5)以及道路交叉口交通延误时间计算模型(11)，得到城市道路路段车辆总行程时间计算模型，如下所示：

式中：T为城市道路路段及其下游信控道路交叉口车辆总行程时间，s/veh；L为城市道路路段长度，km；其他变量如前所定义。

5模型计算与验证

至此已经推导出城市道路车辆行程时间计算模型，并且采用2014年9月22日至9月28日，每天下午4：30-6：30，在长沙市潇湘中路，新民路口-桃子湖路口、桃子湖路口-牌楼路口、牌楼路口-天马路口3个道路路段由北向南的交通调查数据标定了模型各参数，本节采用上述3个道路路段由南向北的交通调查数据，进行模型的计算与验证。

实际观测值与模型计算结果对比及误差分析如图6～图8和表4所示。

从各道路路段及其下游信控道路交叉口的车辆行程时间对比曲线和误差分析表可以看出，本文模型计算值与实际观测值有很好的相关性，同时计算出的3个路段的平均绝对误差为7.18，平均相对误差为0.039，平均绝对相对误差为0.084，平均均方根误差为8.42，误差值均很小，且在可接受范围内。说明在所调查区域内，本文城市道路路段行程时间计算模型有较高的准确度和较强的适用性。

图6　天马路-牌楼路(由南往北)行程时间对比曲线Figure 6　The real and estimated travel time curves on tianma road-pailou road(north bound)

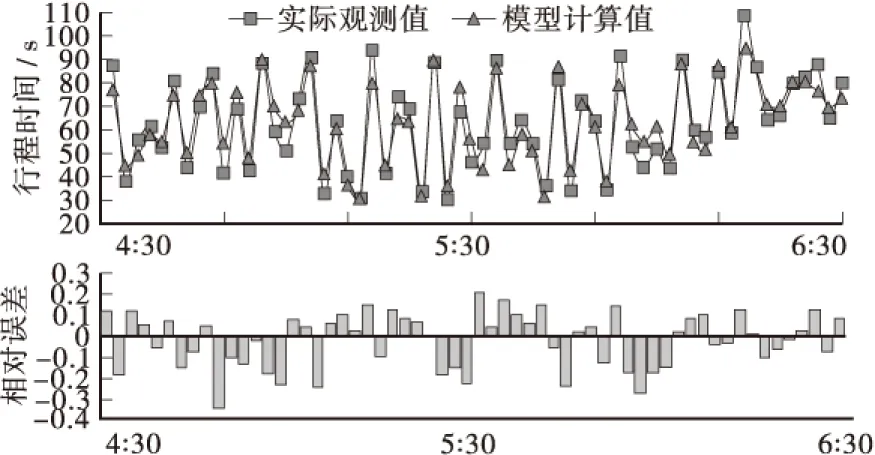
图7　牌楼路-桃子湖(由南往北)行程时间对比曲线Figure 7　The real and estimated travel time curves on pailou road-taozi lake road(north bound)

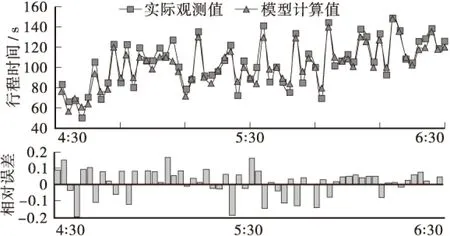
图8　桃子湖路-新民路(由南往北)行程时间对比曲线Figure 8　The real and estimated travel time curves on taozi lake road-xinmin road(north bound)

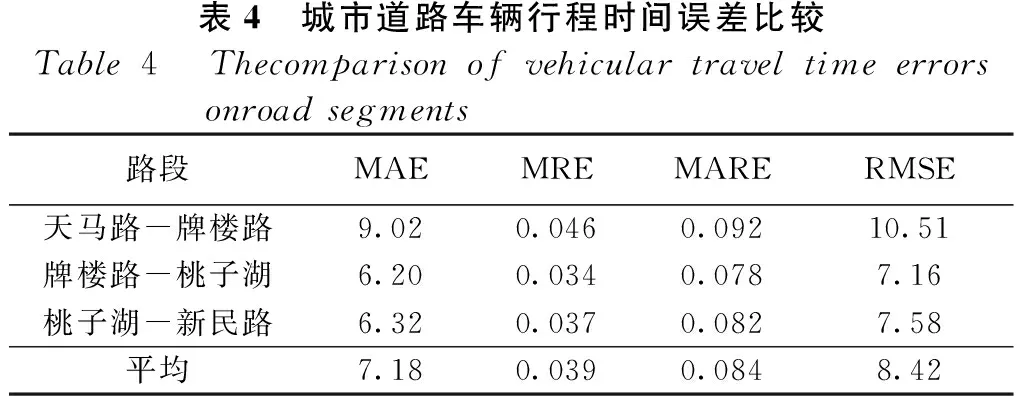
表4 城市道路车辆行程时间误差比较Table4 Thecomparisonofvehiculartraveltimeerrorsonroadsegments路段MAEMREMARERMSE天马路-牌楼路9.020.0460.09210.51牌楼路-桃子湖6.200.0340.0787.16桃子湖-新民路6.320.0370.0827.58平均7.180.0390.0848.42

6结论

在计算车辆在城市道路路段及其下游信控道路交叉口的行程时间时，根据道路交通流在城市道路路段上的两种不同的状态，将车辆在城市道路路段的行程时间分为车辆在城市道路路段上游的行程时间和在其下游信控道路交叉口处的交通延误时间两部分，并且分别建立模型，同时标定相应参数，并进行了计算验证。计算结果表明，在运用本文计算模型进行相关城市道路路段车辆行程时间时，有着较高的准确性与较强的适用性。

[参考文献]

[1]IwaoOkotani，YorgosJStephanedes.DynamicPredictionofTrafficVolumethroughKalmanFilteringTheory[J].TransportationResearchPartB，1994，1(8B)：1-11.

[2]Doughcrty，M.S，H.R.Kirby，andR.Eboyle.TheUseofNeuralNetworkstoRecognizeandPredictTrafficCongestion.TrafficEngineeringandControl，V01.34No.6，1993：311-314.

[3]李硕，范炳全.信号道路网动态路段行程时间有度排队模型[J].系统工程学报，2005(06)：591-599.

[4]杨显立，许伦辉，周勇.基于小波神经网络的道路交通流量实时预测模型研究[J].公路交通技术，2013(05)：111-114.

[5]李嘉，刘小兰.基于卡尔曼滤波理论的交通信息预测模型及其应用[J].中南公路工程，2005(04)：108-109+123.

[6]郑远，杜豫川，孙立军.美国联邦公路局路阻函数探讨[J].交通与运输：学术版，2007(01)：24-26.

[7]李鑫，陆化普.基于视频识别检测数据的机动车OD分析[J].公路工程，2014(05)：170-174+188.

[8]李硕，范炳全.动态与随机交通网络模型及其在智能交通系统中的应用[M].上海：同济大学出版社，2005(03).

[9]陈河明，李硕，高岩，等.信号交叉口期望交通延误模型及计算方法研究[J].交通运输系统工程与信息，2013，13(3)：170-178.

ResearchontheCalculationModelsofVehicleTravelTimeonUrbanRoadSegments

LIAng，LIShuo，LILing

(CollegeofCivilEngineering，HunanUniversity，Changsha，Hunan410082，China)

[Abstract]According to the calculation and prediction for vehicular link travel time on urban road segments as well as at its downstream intersection，this paper chooses the typical road segments and signalized intersections in the urban road network and uses the scientific method to get basic traffic information such as video camera.Based on theanalysis of traffic flowcharacteristics of the road and signalized intersections，this paper reestablishes andcalibrates the travel timecalculation model onroad segments and thedelaymodel at its downstream signalized intersections.Through the calculation and analysis of an example，the results show that the model has good applicability and accuracy.

[Key words]travel time； urban road； calculation model

[收稿日期]2015-03-23

[作者简介]李昂(1989-)，男，河南洛阳人，硕士研究生，研究方向为交通规划与管理。

[中图分类号]U 491.1+4

[文献标识码]A

[文章编号]1674-0610(2016)03-0193-05