基于SOVA的固定时延咬尾卷积码译码算法

李朋飞，张福洪，易志强

(杭州电子科技大学通信工程学院，浙江 杭州 310018)



基于SOVA的固定时延咬尾卷积码译码算法

李朋飞，张福洪，易志强

(杭州电子科技大学通信工程学院，浙江 杭州 310018)

摘要：针对咬尾卷积码最大似然译码算法复杂度过高，循环维特比算法及其低复杂度改进算法译码延迟不固定的缺点，提出了一种基于软输出维特比译码(SOVA)的咬尾卷积码译码算法，算法在降低译码复杂度的同时使译码算法保持固定的译码延迟.算法的主要思想是：在正式译码之前，采用经过修改的SOVA算法确定编码寄存器的初始状态，进而把咬尾卷积码的译码算法转化为普通卷积码的译码算法.仿真结果表明，在误比特率性能上，该算法比较接近最大似然译码算法，并且优于循环维特比译码算法.

关键词：咬尾卷积码；软输出viterbi算法；固定时延；软信息

0引言

咬尾卷积码常见的译码方法有最大似然(Maximum Likelihood，ML)译码算法[1]，循环维特比译码算法(Circular Viterbi Algorithm，CVA)[2]，以及基于循环维特比译码的其他改进算法，例如环绕维特比算法(Wrap Around Viterbi Algorithm，WAVA)[3]，双回溯循环维特比算法(Double Traceback Viterbi Algorithm，DTVA)[4].最大似然译码算法虽然是咬尾卷积码的最优译码算法，但其译码的复杂度也是最高的.文献[5]提出了一种基于ML的改进算法，降低了ML译码算法的复杂度.文献[6]根据咬尾卷积码的循环特性和收敛规则提出了一种基于维特比算法的改进算法.文献[7]根据咬尾卷积码的循环特性提出了一种基于软输入软输出维特比算法的咬尾卷积码译码算法.以上提到的这些算法的迭代次数随着信噪比的变化而变化，其译码延迟是不固定的.为了解决上述译码算法译码延迟不固定的缺点，本文提出了一种固定延迟的咬尾卷积码译码算法，算法在降低译码复杂度的同时使译码算法同样保持着固定的译码延迟.

1算法描述

咬尾卷积码使用待编码信息的最后几个尾比特来初始化编码寄存器，通过这种方法可以保证编码寄存器拥有相同的开始和结束状态.由于咬尾卷积码在编码结束时不再需要额外的信息来迫使编码寄存器恢复到某个特定的状态，因此其编码效率要高于普通卷积码，但其复杂度也明显高于普通卷积码.咬尾卷积码的译码算法之所以比普通卷积码复杂，是因为其译码器没有关于编码器起始状态的先验信息.ML译码算法通过尝试每个可能的初始和结束状态来解决这个问题.CVA算法及其改进算法则利用咬尾卷积码的循环特性[8]，重复地对接收到的待译码信息进行译码，直到某次译码结果满足某个预先设定的停止条件或者重复的次数达到预先设定的最大次数为止.同上述两类算法不同，本文尝试在正式的译码开始之前，首先确定得到译码器的初始状态，这样咬尾卷积码的译码过程将等同于普通卷积码的译码过程.这里提到的初始状态并不一定是卷积编码器编码开始时的那个状态，可以是编码器在编码过程中经历过的任意一个状态.因为咬尾卷积码具有循环特性，其编码过程中的任意一个状态都可以作为译码过程中的起始状态.

).

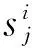
(1)

1)T=0时刻，初始化网格图中所有状态的度量M=0，初始化所有状态的软信息)=+∞；

2)T=T+1时刻，计算网格图中的每个状态的累积度量值；

5)更新软信息的值.找到T时刻到达各个状态的幸存路径和竞争路径中判决比特不相同的判决时刻Tr，并从小到大更新Tr对应的度量值；

6)回到步骤2，直到处理完所有的待译码信息；

7)得到最后的幸存路径及该幸存路径上每个状态对应的软信息.

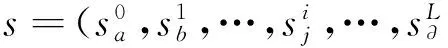
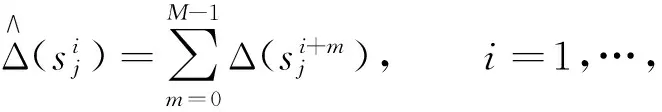
(2)

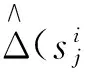
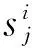
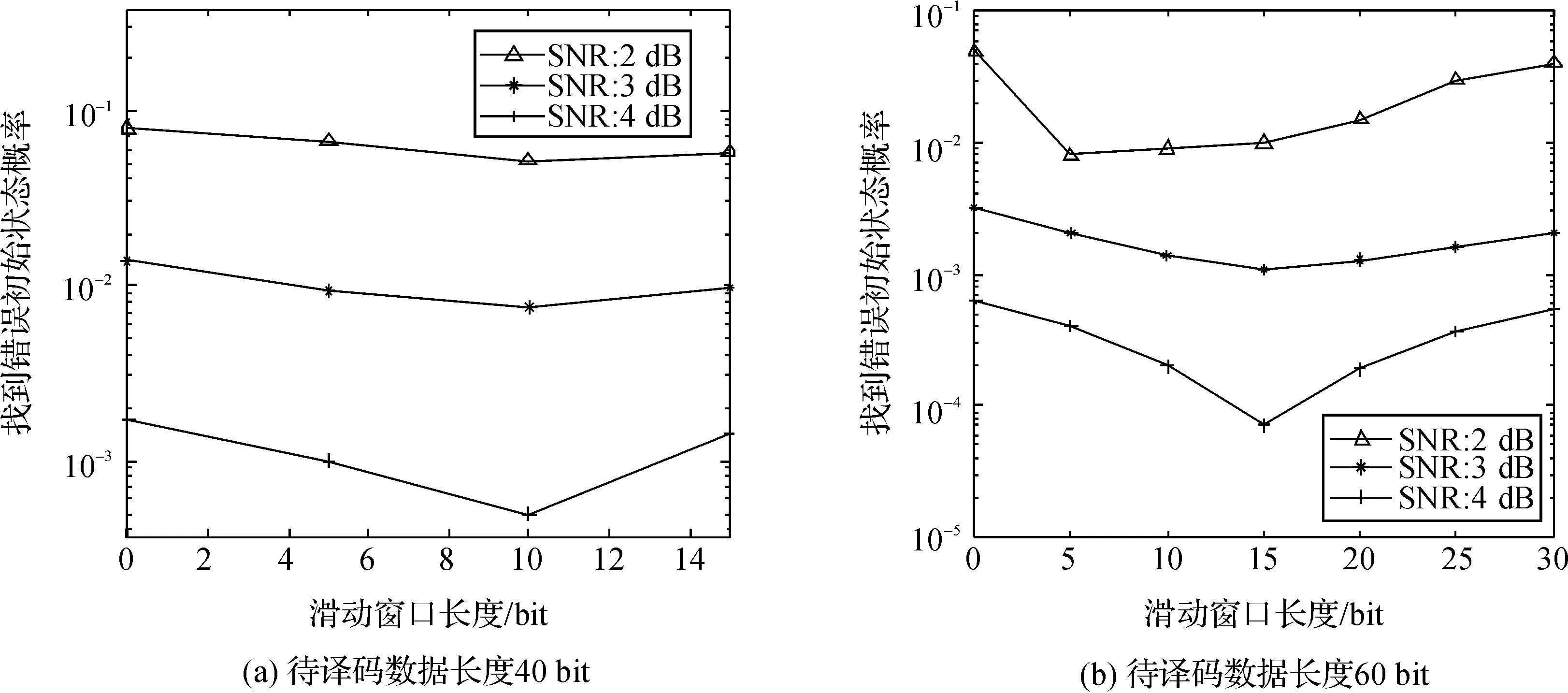
图1　不同窗口长度下找到错误初始状态的概率

图2　调整前的待译码信息

图3　调整后的待译码信息

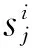
1)采用经过修改的SOVA算法执行第1次译码过程；

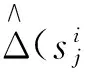
4)根据上面找到的位置对待译码的信息进行调整；

5)以步骤3中找到的状态作为初始和结束状态，对步骤4中经过调整的待译码信息进行维特比译码；

5)对步骤5中得到的译码结果进行调整，得到最后的译码结果.

2算法复杂度分析

下面将以维特比更新次数为指标，对ML算法、CVA算法以及本文提出的算法的计算复杂度进行分析和比较.假设编码器寄存器的个数为M，待编码信息的长度为L.对于普通的维特比算法，其每一次更新过程包含2个步骤：2M个状态分支累积度量值的计算，到达每个状态的幸存路径的选择.因此进行1次普通的维特比译码总共需要更新(2M×L)次.最大似然译码需要2M次互相独立的维特比译码，所以其总的更新次数为(22M×L)次.循环维特比算法需要的迭代次数是不固定的，其迭代的次数跟信噪比有关，假设K为迭代次数，则该算法总共需要(2M×L×K)次更新操作.本文算法总共需要进行2次维特比运算，其涉及到的更新操作为(2M+1×L)次.确定初始状态需要的额外操作包括为了得到软信息而进行的减法，软信息的更新以及平均似然值的计算.这些附加的操作只会影响本算法的第1步，与维特比的更新操作相比可以忽略不计，所以新算法需要的总的更新次数为(2M+1×L)次.从上面的分析可以看出，本文提出的算法的复杂度要远低于ML译码算法.循环维特比算法的计算复杂度与迭代次数有关，是一个不固定的值.本文中算法的计算量是一个固定的值，并不会随着信噪比改变而改变.

3仿真及分析

3.1仿真流程

本文采用MATLAB对文中提出的译码算法及ML和CVA译码算法的误比特率性能进行了仿真.仿真条件如下：仿真时所用的信道为AWGN信道和瑞利衰落信道道，待译码数据块的长度分别为80bit和120bit，调制方式为BPSK调制，编码方式采用生成多项式为[171,133]的(2,1,6)咬尾卷积码.

3.2结果分析

图4和图5分别比较了在AWGN信道和瑞利衰落信道下本文提出的译码算法与ML，CVA算法对不同长度待译码数据块的误比特率，从中可以看出本文提出的算法在保持固定译码延迟的同时其误比特率性能仍优于CVA算法.

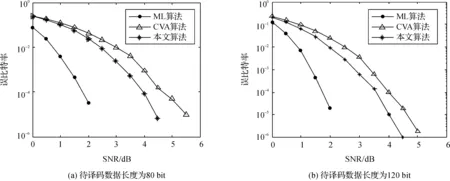
图4　高斯信道下不同长度待译码数据的误码率曲线

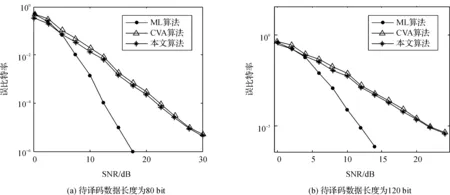
图5　瑞利衰落信道下不同长度待译码数据的误码率曲线

4结束语

本文提出了一种固定延迟的咬尾卷积码译码算法，通过研究分析可知，本文提出的新算法在译码复杂度上远低于ML译码算法，其译码复杂度约为普通维特比译码算法的2倍；在高斯信道下与CVA算法相比，新算法的误比特率性能有了显著地提高，但在瑞利衰落信道下，新算法的优越性并不明显.因此，进一步提高新算法在瑞利衰落信道下的性能将具有更好的应用价值.

参考文献

[1]PAIHT,HANYS,WUTY,etal.Low-complexityMLdecodingforconvolutionaltail-bitingcodes[J].CommunicationsLetters,IEEE, 2008, 12(12): 883-885.

[2]COXRV,SUNDBERGCEW.AnefficientadaptivecircularViterbialgorithmfordecodinggeneralizedtailbitingconvolutionalcodes[J].VehicularTechnology,IEEETransactionson, 1994, 43(1): 57-68.

[3]SHAORY,LINS,FOSSORIERMPC.Twodecodingalgorithmsfortailbitingcodes[J].Communications,IEEETransactionson, 2003, 51(10): 1658-1665.

[4]MINZ,JUNWEIH,JIEM,etal.Researchonan-baseddecodeoftail-bitingconvolutionalcodesandtheirperformanceanalysesusedinLTEsystem[C]//InformationTechnologyandApplications, 2009.IFITA′09.InternationalForumon.IEEE, 2009, 2: 303-306.

[5]QIANH,WANGX,KANGK,etal.ADepth-FirstMLDecodingAlgorithmforTail-BitingTrellises[J].VehicularTechnology,IEEETransactionson, 2015, 64(8):3339-3346.

[6]LID,YANGJ.Efficientimplementationofthedecoderfortailbitingconvolutionalcodes[C]//SignalProcessing,CommunicationsandComputing(ICSPCC), 2014IEEEInternationalConferenceon.IEEE, 2014: 623-626.

[7]FEDORENKOSV,TREFILOVM,WEIY.Improvedlistdecodingoftail-bitingconvolutionalcodes[C]//ProblemsofRedundancyinInformationandControlSystems(REDUNDANCY), 2014XIVInternationalSymposiumon.IEEE, 2014: 35-38.

[8]王晓涛,刘振华.基于可信位置排序的咬尾卷积码译码算法[J].电子与信息学报,2015，37(7):1575-1579.

TheDecodingAlgorithmofTailbitingConvolutionalCodeBasedonSOVA

LIPengfei,ZHANGFuhong,YIZhiqiang

(School of Communication Engineering, Hangzhou Dianzi University, Hangzhou Zhejiang 310018, China)

Abstract：The complexity of maximum likelihood decoding algorithm for Tailbiting convolutional codes is too high. The delay of circular Viterbi algorithm and its improved algorithm of low complexity for Tailbiting convolutional codes is not fixed. In this paper, we propose a decoding algorithm based on the soft-output Viterbi-algorithm(SOVA), this algorithm reduces the decoding complexity and has a fixed decoding delay. The main idea of the algorithm is to use a modified version of the SOVA to determine the initial state of the encoding register before the formal decoding, and then transform the decoding algorithm of the Tailbiting convolutional codes into the decoding algorithm of the common convolutional code. Simulation results are close to the performance of the maximum-likelihood decoding, and better than the circular Viterbi algorithm.

Key words：Tailbiting convolutional codes; SOVA; fixed delay; soft metric

DOI：10.13954/j.cnki.hdu.2016.04.006

收稿日期：2015-12-16

作者简介：李朋飞(1989-)，男，河南安阳人，硕士研究生，信号与信息处理.通信作者：张福洪教授，E-mail：fuhong@vip.sina.com.

中图分类号：TN929.5

文献标识码：A

文章编号：1001-9146(2016)04-0024-05